华师大版的九年级上册第23章 图形的相似—23.6 图形与坐标 2.图形的变换与坐标 同步练习
文档属性
| 名称 | 华师大版的九年级上册第23章 图形的相似—23.6 图形与坐标 2.图形的变换与坐标 同步练习 |
|
|
| 格式 | doc | ||
| 文件大小 | 218.5KB | ||
| 资源类型 | 素材 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2016-06-24 08:57:28 | ||
图片预览


文档简介
登陆21世纪教育 助您教考全无忧
华师大版数学九年级上册第23章第6节23.6.2图形的变换与坐标
同步练习
一、选择题
1. 点M(-2,1)关于x轴的对称点N的坐标是( )
A.(2,1) B.(-2,1) C.(-2,-1) D.(2,-1)
答案:C
解析:解答:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
∴点M(-2,1)关于x轴的对称点的坐标是(-2,-1),
故选:C.
分析:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数即可得出结果.
2. 在平面直角坐标系中,点M(-2,1)关于x轴对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C
解析:解答:点M(-2,1)关于x轴对称的点在(-2,-1),在第三象限,
故选:C.
分析:根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得点M(-2,1)关于x轴对称的点的坐标,再根据点的坐标符号可得所在象限.
3. 在平面直角坐标系中,点(4,-5)关于x轴对称点的坐标为( )
A.(4,5) B.(-4,-5) C.(-4,5) D.(5,4)
答案:A
解析:解答:根据关于x轴对称点的坐标特点,可得
点(4,-5)关于x轴对称点的坐标为(4,5).
故选:A.
分析:关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,据此求出点(4,-5)关于x轴对称点的坐标为多少即可.
4. 在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
A.(-3,-2) B.(3,2) C.(2,-3) D.(3,-2)
答案:C
解析:解答:点P关于直线y=x对称点为点Q,
作AP∥x轴交y=x于A,
∵y=x是第一、三象限的角平分线,
∴点A的坐标为(2,2),
∵AP=AQ,
∴点Q的坐标为(2,-3)
故选:C.
分析:根据直线y=x是第一、三象限的角平分线,和点P的坐标结合图形得到答案.
5. 已知点A(4,3)和点B是坐标平面内的两个点,且它们关于过点(-3,0)与y轴平行的直线对称,则点B的坐标是( )
A.(1,3) B.(-10,3) C.(4,3) D.(4,1)
答案:B
解析:解答:点(-3,0)与y轴平行的直线为直线x=-3,
∵点A、B关于直线x=-3对称,
∴点B的纵坐标为3,
设点B的横坐标为x,
则
解得x=-10,
所以,点B的坐标为(-10,3).
故选B.
分析:根据关于平行于y轴的直线的对称点的纵坐标相等求出点B的纵坐标是3,再根据轴对称的性质求出点B的横坐标,然后写出即可.
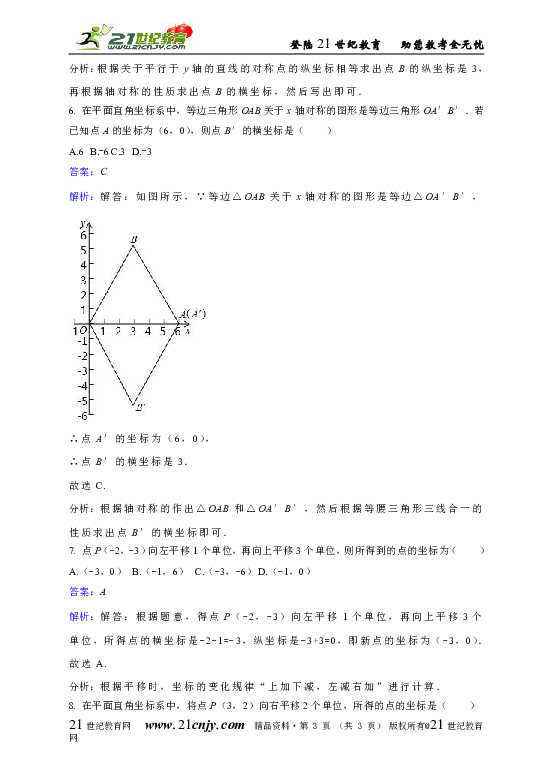
6. 在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),则点B′的横坐标是( )
A.6 B.-6 C.3 D.-3
答案:C
解析:解答:如图所示,∵等边△OAB关于x轴对称的图形是等边△OA′B′,
∴点A′的坐标为(6,0),
∴点B′的横坐标是3.
故选C.
分析:根据轴对称的作出△OAB和△OA′B′,然后根据等腰三角形三线合一的性质求出点B′的横坐标即可.
7. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A.(-3,0) B.(-1,6) C.(-3,-6) D.(-1,0)
答案:A
解析:解答:根据题意,得点P(-2,-3)向左平移1个单位,再向上平移3个单位,所得点的横坐标是-2-1=-3,纵坐标是-3+3=0,即新点的坐标为(-3,0).
故选A.
分析:根据平移时,坐标的变化规律“上加下减,左减右加”进行计算.
8. 在平面直角坐标系中,将点P(3,2)向右平移2个单位,所得的点的坐标是( )
A.(1,2) B.(3,0) C.(3,4) D.(5,2)
答案:D
解析:解答:将点P(3,2)向右平移2个单位,所得的点的坐标是(3+2,2),即(5,2).
故选D.
分析:将点P(3,2)向右平移2个单位后,纵坐标不变,横坐标加上2即可得到平移后点的坐标.
9. 将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度后得到点A′的坐标为( )
A.(-4,-2 ) B.(2,-2 ) C.(-4,6 ) D.(2,6 )
答案:B
解析:解答:∵点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点A′,
∴A′的坐标是(-1+3,2-4),即:(2,-2).
故选B.
分析:根据点的平移规律,左右移,横坐标减加,纵坐标不变;上下移,纵坐标加减,横坐标不变即可求出答案.
10. 在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m-n=-3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选A.
分析:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,则m=2且n=-3,从而得出点M(m,n)所在的象限.
11. 在平面直角坐标系中,点A(1,3)关于原点O对称的点A′的坐标为( )
A.(-1,3) B.(1,-3) C.(3,1) D.(-1,-3)
答案:D
解析:解答:点A(1,3)关于原点O对称的点A′的坐标为(-1,-3).
故选:D.
分析:根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可直接得到答案.
12. 已知点A(a,2013)与点A′(-2014,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
答案:A
解析:解答:∵点A(a,2013)与点A′(-2014,b)是关于原点O的对称点,
∴a=2014,b=-2013,
则a+b的值为:2014-2013=1.
故选:A.
分析:根据关于原点对称的点,横坐标与纵坐标都互为相反数解答.
13. 在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)
答案:D
解析:解答:根据题意得,点P关于原点的对称点是点P′,
∵P点坐标为(-3,2),
∴点P′的坐标(3,-2).
故选:D.
分析:将点P绕原点O顺时针旋转180°,实际上是求点P关于原点的对称点的坐标.
14. 在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转180°得到OA′,则点A′在平面直角坐标系中的位置是在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C
解析:解答:
如图,∵点A(2,3),若将OA绕原点O逆时针旋转180°得到OA′,
∴A′的坐标是(-2,-3),
即点A′在第三象限,
故选C.
分析:画出图形,根据旋转得出A′的坐标,根据坐标得出答案即可.
15. 在平面直角坐标系中,点A(3,20)绕原点旋转180°后所得点的坐标为( )
A.(-3,20) B.(3,-20) C.(-3,-20) D.(20,-3)
答案:C
解析:解答:∵点A(3,20)绕原点旋转180°后所得点与点A关于坐标原点对称,
∴所得的点的横坐标为-3,纵坐标为-20,
∴点的坐标为(-3,-20).
故选C.
分析:根据绕原点旋转180°后两点关于原点对称,再根据关于坐标原点对称的点的横坐标互为相反数,纵坐标互为相反数解答.
二、填空题
16. 在平面直角坐标系中,点(-3,2)关于y轴的对称点的坐标是
答案:(3,2)
解析:解答:在平面直角坐标系中,点(-3,2)关于y轴的对称点的坐标是(3,2),
故答案为:(3,2).
分析:根据关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
17. 点P(1,2)关于直线y=1对称的点的坐标是 .
答案:(1,0)
解析:解答:点P(1,2)关于直线y=1对称的点的坐标是(1,0).
分析:点P(1,2)关于直线y=1对称的点与点P的连线平行于y轴,因而横坐标与P的横坐标相同,纵坐标与2的平均数是1,因而纵坐标是0.
18. 在平面直角坐标系中,有一条线段AB,已知点A(-2,0)和B(0,2),平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(1,3),则线段A1B1的中点坐标是 .
答案:(2,4)
解析:解答:∵点A(-2,0),点A的对应点A1的坐标为(1,3),
∴点A向右平移了3个单位,又向上平移了3个单位,
∴B的平移方式也是向右平移了3个单位,又向上平移了3个单位,
∵B(0,2),
∴B1的点(3,5),
∴A1B1的中点(),
即(2,4).
故答案为:(2,4).
分析:首先根据A点和A1的坐标可得点A向右平移了3个单位,又向上平移了3个单位,进而可得B1的点(3,5),再根据求出中点坐标.
19. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为 .
答案:7
解析:解答:∵点P(-20,a)与点Q(b,13)关于原点对称,
∴b=20,a=-13,
∴a+b=20-13=7,
故答案为:7.
分析:首先根据关于原点对称的点的坐标特点可得a、b的值,然后在计算a+b的值.
20. 在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB,连接线段AB,若直线y=kx-2与△OAB有交点,则k的取值范围是
答案:k≤-3或k≥1.
解析:解答:如图,点A(-2,4)绕原点顺时针转90°后的对应点B的坐标为(4,2),
直线经过点A时,-2k-2=4,
解得k=-3,
直线经过点B时,4k-2=2,
解得k=1,
所以,直线y=kx-2与△OAB有交点时k的取值范围是k≤-3或k≥1.
故答案为:k≤-3或k≥1.
分析:作出图形,然后求出直线经过点A、B时的k值,再写出k的取值范围即可.
三、解答题
21. 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
(1)直接写出点D1的坐标;
答案:解答:
D1(-3,0).
(2)求点D旋转到点D1所经过的路线长.
答案:解答:∵正方形ABCO的边长为4,D为AB上一点,且BD=3,
根据勾股定理可求得CD=5.
∴点D旋转到点D1
所经过的路线长为×2π×5=π.
解析:(1)把△CBD顺时针旋转90°,得到△CB1D1.如图所示,B1D1=BD=3,D1在x轴负半轴上,所以D1(-3,0).
(2)路线是以C为圆心,CD为半径,圆心角为90°的扇形的弧.根据弧长公式求解.
22. 如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
答案:解答:(1)如图可得△A′B′C′
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:
答案:解答: 如上图,以点A为坐标原点建立平面直角坐标系,则B(1,2);B′(3,5).
解析:(1)把3个顶点向上平移2个单位,顺次连接个顶点即可;
(2)以点A为坐标原点,建立平面直角坐标系,找到所求点的坐标即可.
23. 已知Rt△AOB的两条直角边OA=3,OB=1,分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系,如图所示.先将Rt△AOB绕原点O按顺时针方向旋转90°后,再沿x轴负方向平移1个单位长度得到△CDO.
(1)直接写出点A、C的坐标;
(2)求顶点A所经过的路径总长.
答案:解答:
(1)A(3,0),C(-1,-3);
(2)∵A所经过的路径总长包括一段弧以及一条线段长度,
∴
CA′=1,
∴顶点A所经过的路径总长为:
解析:(1)根据直角边OA=3,OB=1,直接得出点A、C的坐标;
(2)根据A所经过的路径总长包括一段弧以及一条线段长度,分别求出即可.
24. 将图中的△ABC作下列运动,画出相应的图形:
(1)关于y 轴对称图形:△ADE;
答案:解答:(1)如图所示:
(2)以B点为位似中心,将△ABC放大到图形△BFG,使位似比为1:2
答案:解答:如图所示:△BFG是将△ABC放大到2倍的图形;
(3)写出你所画图形的坐标.
答案:解答: A(0,-2)D(-3,-1)E(-2,1),
B(3,-1)F(-3,-3)G(1,3).
解析:(1)根据轴对称的性质找三角形各点的轴对称点,并顺次连接即可;
(2)延长BA,到F,使BF=2AB,延长BC,到G,使BG=2CB,连接GB、BF、FG就是所画的位似三角形;.
(3)根据图形即可写出相应顶点的坐标.
25. 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)求边OA在旋转过程中所扫过的面积;
答案:解答:(1)∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
∴OA旋转了45°.
∴OA在旋转过程中所扫过的面积为
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
答案:解答:∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.
∴∠BMN=∠BNM.∴BM=BN.
又∵BA=BC,∴AM=CN.
又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.
∴∠AOM=∠CON=(∠AOC-∠MON)=(90°-45°)=22.5°.
∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°-22.5°=22.5°.
(3)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
答案:解答:在旋转正方形OABC的过程中,p值无变化.
证明:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
∴△OAE≌△OCN.
∴OE=ON,AE=CN.
又∵∠MOE=∠MON=45°,OM=OM,
∴△OME≌△OMN.∴MN=ME=AM+AE.
∴MN=AM+CN,
∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形OABC的过程中,p值无变化.
解析:(1)根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积;
(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;
(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
华师大版数学九年级上册第23章第6节23.6.2图形的变换与坐标
同步练习
一、选择题
1. 点M(-2,1)关于x轴的对称点N的坐标是( )
A.(2,1) B.(-2,1) C.(-2,-1) D.(2,-1)
答案:C
解析:解答:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数,
∴点M(-2,1)关于x轴的对称点的坐标是(-2,-1),
故选:C.
分析:根据两点关于x轴对称,横坐标不变,纵坐标互为相反数即可得出结果.
2. 在平面直角坐标系中,点M(-2,1)关于x轴对称的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C
解析:解答:点M(-2,1)关于x轴对称的点在(-2,-1),在第三象限,
故选:C.
分析:根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得点M(-2,1)关于x轴对称的点的坐标,再根据点的坐标符号可得所在象限.
3. 在平面直角坐标系中,点(4,-5)关于x轴对称点的坐标为( )
A.(4,5) B.(-4,-5) C.(-4,5) D.(5,4)
答案:A
解析:解答:根据关于x轴对称点的坐标特点,可得
点(4,-5)关于x轴对称点的坐标为(4,5).
故选:A.
分析:关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数,据此求出点(4,-5)关于x轴对称点的坐标为多少即可.
4. 在平面直角坐标系中,点P(-3,2)关于直线y=x对称点的坐标是( )
A.(-3,-2) B.(3,2) C.(2,-3) D.(3,-2)
答案:C
解析:解答:点P关于直线y=x对称点为点Q,
作AP∥x轴交y=x于A,
∵y=x是第一、三象限的角平分线,
∴点A的坐标为(2,2),
∵AP=AQ,
∴点Q的坐标为(2,-3)
故选:C.
分析:根据直线y=x是第一、三象限的角平分线,和点P的坐标结合图形得到答案.
5. 已知点A(4,3)和点B是坐标平面内的两个点,且它们关于过点(-3,0)与y轴平行的直线对称,则点B的坐标是( )
A.(1,3) B.(-10,3) C.(4,3) D.(4,1)
答案:B
解析:解答:点(-3,0)与y轴平行的直线为直线x=-3,
∵点A、B关于直线x=-3对称,
∴点B的纵坐标为3,
设点B的横坐标为x,
则
解得x=-10,
所以,点B的坐标为(-10,3).
故选B.
分析:根据关于平行于y轴的直线的对称点的纵坐标相等求出点B的纵坐标是3,再根据轴对称的性质求出点B的横坐标,然后写出即可.
6. 在平面直角坐标系中,等边三角形OAB关于x轴对称的图形是等边三角形OA′B′.若已知点A的坐标为(6,0),则点B′的横坐标是( )
A.6 B.-6 C.3 D.-3
答案:C
解析:解答:如图所示,∵等边△OAB关于x轴对称的图形是等边△OA′B′,
∴点A′的坐标为(6,0),
∴点B′的横坐标是3.
故选C.
分析:根据轴对称的作出△OAB和△OA′B′,然后根据等腰三角形三线合一的性质求出点B′的横坐标即可.
7. 点P(-2,-3)向左平移1个单位,再向上平移3个单位,则所得到的点的坐标为( )
A.(-3,0) B.(-1,6) C.(-3,-6) D.(-1,0)
答案:A
解析:解答:根据题意,得点P(-2,-3)向左平移1个单位,再向上平移3个单位,所得点的横坐标是-2-1=-3,纵坐标是-3+3=0,即新点的坐标为(-3,0).
故选A.
分析:根据平移时,坐标的变化规律“上加下减,左减右加”进行计算.
8. 在平面直角坐标系中,将点P(3,2)向右平移2个单位,所得的点的坐标是( )
A.(1,2) B.(3,0) C.(3,4) D.(5,2)
答案:D
解析:解答:将点P(3,2)向右平移2个单位,所得的点的坐标是(3+2,2),即(5,2).
故选D.
分析:将点P(3,2)向右平移2个单位后,纵坐标不变,横坐标加上2即可得到平移后点的坐标.
9. 将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度后得到点A′的坐标为( )
A.(-4,-2 ) B.(2,-2 ) C.(-4,6 ) D.(2,6 )
答案:B
解析:解答:∵点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个长度单位后得到点A′,
∴A′的坐标是(-1+3,2-4),即:(2,-2).
故选B.
分析:根据点的平移规律,左右移,横坐标减加,纵坐标不变;上下移,纵坐标加减,横坐标不变即可求出答案.
10. 在平面直角坐标系中,若点P(m,m-n)与点Q(-2,3)关于原点对称,则点M(m,n)在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:A
解析:解答:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,
∴m=2且m-n=-3,
∴m=2,n=5
∴点M(m,n)在第一象限,
故选A.
分析:根据平面内两点关于原点对称的点,横坐标与纵坐标都互为相反数,则m=2且n=-3,从而得出点M(m,n)所在的象限.
11. 在平面直角坐标系中,点A(1,3)关于原点O对称的点A′的坐标为( )
A.(-1,3) B.(1,-3) C.(3,1) D.(-1,-3)
答案:D
解析:解答:点A(1,3)关于原点O对称的点A′的坐标为(-1,-3).
故选:D.
分析:根据关于原点对称的点的坐标特点:两个点关于原点对称时,它们的坐标符号相反可直接得到答案.
12. 已知点A(a,2013)与点A′(-2014,b)是关于原点O的对称点,则a+b的值为( )
A.1 B.5 C.6 D.4
答案:A
解析:解答:∵点A(a,2013)与点A′(-2014,b)是关于原点O的对称点,
∴a=2014,b=-2013,
则a+b的值为:2014-2013=1.
故选:A.
分析:根据关于原点对称的点,横坐标与纵坐标都互为相反数解答.
13. 在平面直角坐标系中,把点P(-3,2)绕原点O顺时针旋转180°,所得到的对应点P′的坐标为( )
A.(3,2) B.(2,-3) C.(-3,-2) D.(3,-2)
答案:D
解析:解答:根据题意得,点P关于原点的对称点是点P′,
∵P点坐标为(-3,2),
∴点P′的坐标(3,-2).
故选:D.
分析:将点P绕原点O顺时针旋转180°,实际上是求点P关于原点的对称点的坐标.
14. 在平面直角坐标系xOy中,已知点A(2,3),若将OA绕原点O逆时针旋转180°得到OA′,则点A′在平面直角坐标系中的位置是在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
答案:C
解析:解答:
如图,∵点A(2,3),若将OA绕原点O逆时针旋转180°得到OA′,
∴A′的坐标是(-2,-3),
即点A′在第三象限,
故选C.
分析:画出图形,根据旋转得出A′的坐标,根据坐标得出答案即可.
15. 在平面直角坐标系中,点A(3,20)绕原点旋转180°后所得点的坐标为( )
A.(-3,20) B.(3,-20) C.(-3,-20) D.(20,-3)
答案:C
解析:解答:∵点A(3,20)绕原点旋转180°后所得点与点A关于坐标原点对称,
∴所得的点的横坐标为-3,纵坐标为-20,
∴点的坐标为(-3,-20).
故选C.
分析:根据绕原点旋转180°后两点关于原点对称,再根据关于坐标原点对称的点的横坐标互为相反数,纵坐标互为相反数解答.
二、填空题
16. 在平面直角坐标系中,点(-3,2)关于y轴的对称点的坐标是
答案:(3,2)
解析:解答:在平面直角坐标系中,点(-3,2)关于y轴的对称点的坐标是(3,2),
故答案为:(3,2).
分析:根据关于y轴对称的点,纵坐标相同,横坐标互为相反数,可得答案.
17. 点P(1,2)关于直线y=1对称的点的坐标是 .
答案:(1,0)
解析:解答:点P(1,2)关于直线y=1对称的点的坐标是(1,0).
分析:点P(1,2)关于直线y=1对称的点与点P的连线平行于y轴,因而横坐标与P的横坐标相同,纵坐标与2的平均数是1,因而纵坐标是0.
18. 在平面直角坐标系中,有一条线段AB,已知点A(-2,0)和B(0,2),平移线段AB得到线段A1B1.若点A的对应点A1的坐标为(1,3),则线段A1B1的中点坐标是 .
答案:(2,4)
解析:解答:∵点A(-2,0),点A的对应点A1的坐标为(1,3),
∴点A向右平移了3个单位,又向上平移了3个单位,
∴B的平移方式也是向右平移了3个单位,又向上平移了3个单位,
∵B(0,2),
∴B1的点(3,5),
∴A1B1的中点(),
即(2,4).
故答案为:(2,4).
分析:首先根据A点和A1的坐标可得点A向右平移了3个单位,又向上平移了3个单位,进而可得B1的点(3,5),再根据求出中点坐标.
19. 在平面直角坐标系中,点P(-20,a)与点Q(b,13)关于原点对称,则a+b的值为 .
答案:7
解析:解答:∵点P(-20,a)与点Q(b,13)关于原点对称,
∴b=20,a=-13,
∴a+b=20-13=7,
故答案为:7.
分析:首先根据关于原点对称的点的坐标特点可得a、b的值,然后在计算a+b的值.
20. 在平面直角坐标系中,点A坐标为(-2,4),与原点的连线OA绕原点顺时针转90°,得到线段OB,连接线段AB,若直线y=kx-2与△OAB有交点,则k的取值范围是
答案:k≤-3或k≥1.
解析:解答:如图,点A(-2,4)绕原点顺时针转90°后的对应点B的坐标为(4,2),
直线经过点A时,-2k-2=4,
解得k=-3,
直线经过点B时,4k-2=2,
解得k=1,
所以,直线y=kx-2与△OAB有交点时k的取值范围是k≤-3或k≥1.
故答案为:k≤-3或k≥1.
分析:作出图形,然后求出直线经过点A、B时的k值,再写出k的取值范围即可.
三、解答题
21. 如图,正方形ABCO的边长为4,D为AB上一点,且BD=3,以点C为中心,把△CBD顺时针旋转90°,得到△CB1D1.
(1)直接写出点D1的坐标;
答案:解答:
D1(-3,0).
(2)求点D旋转到点D1所经过的路线长.
答案:解答:∵正方形ABCO的边长为4,D为AB上一点,且BD=3,
根据勾股定理可求得CD=5.
∴点D旋转到点D1
所经过的路线长为×2π×5=π.
解析:(1)把△CBD顺时针旋转90°,得到△CB1D1.如图所示,B1D1=BD=3,D1在x轴负半轴上,所以D1(-3,0).
(2)路线是以C为圆心,CD为半径,圆心角为90°的扇形的弧.根据弧长公式求解.
22. 如图,已知单位长度为1的方格中有个△ABC.
(1)请画出△ABC向上平移3格再向右平移2格所得△A′B′C′.
答案:解答:(1)如图可得△A′B′C′
(2)请以点A为坐标原点建立平面直角坐标系(在图中画出),
然后写出点B、点B′的坐标:
答案:解答: 如上图,以点A为坐标原点建立平面直角坐标系,则B(1,2);B′(3,5).
解析:(1)把3个顶点向上平移2个单位,顺次连接个顶点即可;
(2)以点A为坐标原点,建立平面直角坐标系,找到所求点的坐标即可.
23. 已知Rt△AOB的两条直角边OA=3,OB=1,分别以OA、OB所在直线为x轴、y轴建立平面直角坐标系,如图所示.先将Rt△AOB绕原点O按顺时针方向旋转90°后,再沿x轴负方向平移1个单位长度得到△CDO.
(1)直接写出点A、C的坐标;
(2)求顶点A所经过的路径总长.
答案:解答:
(1)A(3,0),C(-1,-3);
(2)∵A所经过的路径总长包括一段弧以及一条线段长度,
∴
CA′=1,
∴顶点A所经过的路径总长为:
解析:(1)根据直角边OA=3,OB=1,直接得出点A、C的坐标;
(2)根据A所经过的路径总长包括一段弧以及一条线段长度,分别求出即可.
24. 将图中的△ABC作下列运动,画出相应的图形:
(1)关于y 轴对称图形:△ADE;
答案:解答:(1)如图所示:
(2)以B点为位似中心,将△ABC放大到图形△BFG,使位似比为1:2
答案:解答:如图所示:△BFG是将△ABC放大到2倍的图形;
(3)写出你所画图形的坐标.
答案:解答: A(0,-2)D(-3,-1)E(-2,1),
B(3,-1)F(-3,-3)G(1,3).
解析:(1)根据轴对称的性质找三角形各点的轴对称点,并顺次连接即可;
(2)延长BA,到F,使BF=2AB,延长BC,到G,使BG=2CB,连接GB、BF、FG就是所画的位似三角形;.
(3)根据图形即可写出相应顶点的坐标.
25. 在平面直角坐标系中,边长为2的正方形OABC的两顶点A、C分别在y轴、x轴的正半轴上,点O在原点.现将正方形OABC绕O点顺时针旋转,当A点第一次落在直线y=x上时停止旋转,旋转过程中,AB边交直线y=x于点M,BC边交x轴于点N(如图).
(1)求边OA在旋转过程中所扫过的面积;
答案:解答:(1)∵A点第一次落在直线y=x上时停止旋转,直线y=x与y轴的夹角是45°,
∴OA旋转了45°.
∴OA在旋转过程中所扫过的面积为
(2)旋转过程中,当MN和AC平行时,求正方形OABC旋转的度数;
答案:解答:∵MN∥AC,
∴∠BMN=∠BAC=45°,∠BNM=∠BCA=45°.
∴∠BMN=∠BNM.∴BM=BN.
又∵BA=BC,∴AM=CN.
又∵OA=OC,∠OAM=∠OCN,∴△OAM≌△OCN.
∴∠AOM=∠CON=(∠AOC-∠MON)=(90°-45°)=22.5°.
∴旋转过程中,当MN和AC平行时,正方形OABC旋转的度数为45°-22.5°=22.5°.
(3)设△MBN的周长为p,在旋转正方形OABC的过程中,p值是否有变化?请证明你的结论.
答案:解答:在旋转正方形OABC的过程中,p值无变化.
证明:延长BA交y轴于E点,
则∠AOE=45°-∠AOM,∠CON=90°-45°-∠AOM=45°-∠AOM,
∴∠AOE=∠CON.
又∵OA=OC,∠OAE=180°-90°=90°=∠OCN.
∴△OAE≌△OCN.
∴OE=ON,AE=CN.
又∵∠MOE=∠MON=45°,OM=OM,
∴△OME≌△OMN.∴MN=ME=AM+AE.
∴MN=AM+CN,
∴p=MN+BN+BM=AM+CN+BN+BM=AB+BC=4.
∴在旋转正方形OABC的过程中,p值无变化.
解析:(1)根据扇形的面积公式来求得边OA在旋转过程中所扫过的面积;
(2)解决本题需利用全等,根据正方形一个内角的度数求出∠AOM的度数;
(3)利用全等把△MBN的各边整理到成与正方形的边长有关的式子.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网 www.21cnjy.com 精品资料·第 13 页 (共 13 页) 版权所有@21世纪教育网
