广东省汕头市潮阳区2025年九年级学业水平模拟考试数学练习卷(含答案)
文档属性
| 名称 | 广东省汕头市潮阳区2025年九年级学业水平模拟考试数学练习卷(含答案) |
|
|
| 格式 | docx | ||
| 文件大小 | 434.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 00:00:00 | ||
图片预览

文档简介
2025年广东省汕头市潮阳区九年级学业水平模拟考试数学练习卷
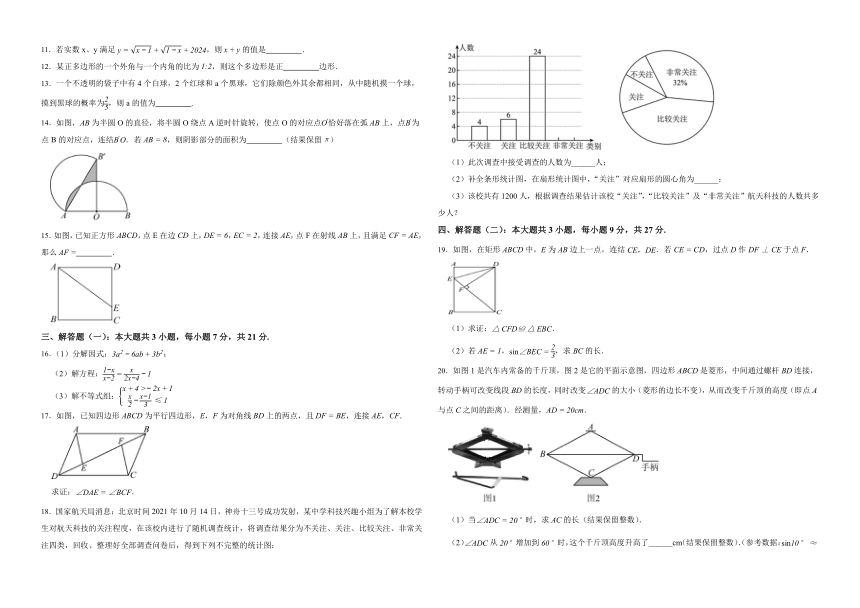
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果支出1000元记作元,那么元表示( )
A.支出80元 B.收入 80元 C.支出1080元 D.收入1080元
2.如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )
A. B.
C. D.
3.2025年1月17日上午,国家统计局发布数据,2024年全年出生人口约为9540000人,9540000用科学记数法表示为( )
A. B. C. D.
4.如图,将一副三角尺按图中所示位置摆放,点在的延长线上,点、分别为直角顶点,且,,若,则的度数是( )
A. B. C. D.
5.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
6.估计的值应在 ( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
7.反比例函数y=的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
8.我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10,…)和“正方形数”(如1,4,9,16,…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A.33 B.301 C.386 D.571
9.如图,在△ABC中,∠C=90°,∠B=15°,AC=l,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则AD的长为( )
A.l.5 B. C.2 D.
10.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3
C.y=﹣3(x+1)2+3 D.y=3(x+1)2+3
二、填空题:本大题共5小题,每小题3分,共15分.
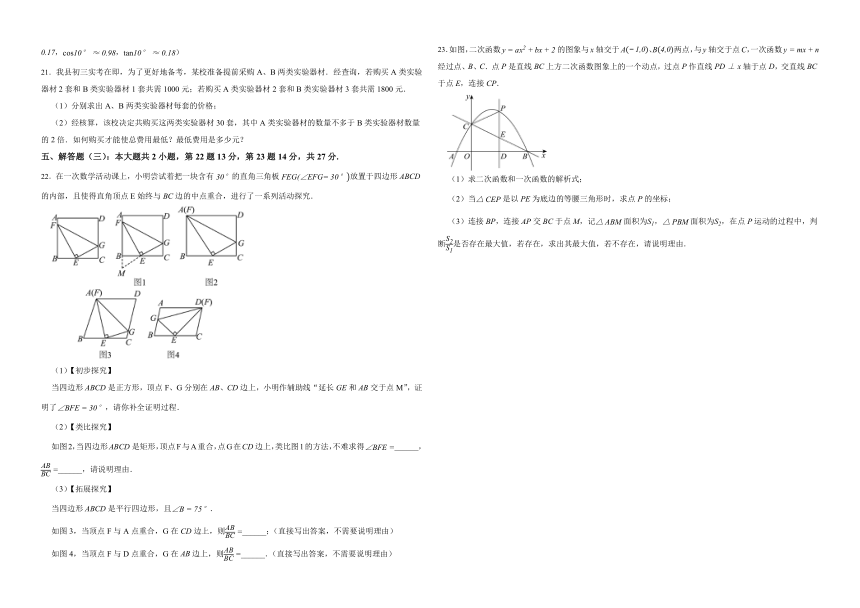
11.若实数x、y满足,则的值是 .
12.某正多边形的一个外角与一个内角的比为,则这个多边形是正 边形.
13.一个不透明的袋子中有4个白球,2个红球和a个黑球,它们除颜色外其余都相同,从中随机摸一个球,摸到黑球的概率为,则a的值为 .
14.如图,为半圆O的直径,将半圆O绕点A逆时针旋转,使点O的对应点恰好落在弧上,点为点B的对应点,连结.若,则阴影部分的面积为 (结果保留)
15.如图,已知正方形,点E在边上,,,连接,点F在射线上,且满足,那么 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.(1)分解因式:;
(2)解方程:
(3)解不等式组:
17.如图,已知四边形为平行四边形,,为对角线上的两点,且,连接,.
求证:.
18.国家航天局消息:北京时间2021年10月14日,神舟十三号成功发射,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图:
(1)此次调查中接受调查的人数为______人;
(2)补全条形统计图,在扇形统计图中,“关注”对应扇形的圆心角为______;
(3)该校共有1200人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,在矩形中,为边上一点,连结.若,过点作于点.
(1)求证:.
(2)若,,求的长.
20.如图1是汽车内常备的千斤顶,图2是它的平面示意图,四边形是菱形,中间通过螺杆连接,转动手柄可改变线段的长度,同时改变的大小(菱形的边长不变),从而改变千斤顶的高度(即点与点之间的距离).经测量,.
(1)当时,求的长(结果保留整数).
(2)从增加到时,这个千斤顶高度升高了______cm(结果保留整数).(参考数据:,,)
21.我县初三实考在即,为了更好地备考,某校准备提前采购A、B两类实验器材.经查询,若购买A类实验器材2套和B类实验器材1套共需1000元;若购买A类实验器材2套和B类实验器材3套共需1800元.
(1)分别求出A、B两类实验器材每套的价格;
(2)经核算,该校决定共购买这两类实验器材30套,其中A类实验器材的数量不多于B类实验器材数量的2倍.如何购买才能使总费用最低?最低费用是多少元?
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.在一次数学活动课上,小明尝试着把一块含有的直角三角板放置于四边形的内部,且使得直角顶点E始终与边的中点重合,进行了一系列活动探究.
(1)【初步探究】
当四边形是正方形,顶点F、G分别在、边上,小明作辅助线“延长和交于点M”,证明了,请你补全证明过程.
(2)【类比探究】
如图2,当四边形是矩形,顶点F与A重合,点G在边上,类比图1的方法,不难求得______,______,请说明理由.
(3)【拓展探究】
当四边形是平行四边形,且.
如图3,当顶点F与A点重合,G在边上,则______;(直接写出答案,不需要说明理由)
如图4,当顶点F与D点重合,G在边上,则______.(直接写出答案,不需要说明理由)
23.如图,二次函数的图象与轴交于、两点,与轴交于点,一次函数经过点、、.点是直线上方二次函数图象上的一个动点,过点作直线轴于点,交直线于点,连接.
(1)求二次函数和一次函数的解析式;
(2)当是以为底边的等腰三角形时,求点的坐标;
(3)连接,连接交于点,记面积为,面积为,在点运动的过程中,判断是否存在最大值,若存在,求出其最大值,若不存在,请说明理由.
参考答案
1.D
2.D
3.C
4.A
5.B
6.D
7.A
8.C
9.C
10.A
11.2025
12.六
13.4
14.
15.2或14
16.解:(1)
;
(2)
整理,可得,
方程左右两边同时乘以可得:
,
解得,
检验:当时,
∴原分式方程的解为;
(3),
解不等式①,可得,
解不等式②,可得,
∴不等式组的解集为.
17.证明:四边形是平行四边形,
,,
,
∵,
∴,即,
在和中
,
,
.
18.(1)50
(2)
(3)1104
19.(1)证明:∵四边形是矩形,∴,,,
∴,
∵,
∴,
∴,
在与中,
,
∴;
(2)解:∵,∴设,,
∴,
∴,
∵,,
∴,
解得,
∴.
20.(1)的长约为
(2)13
21.(1)解:设A类实验器材每套的售价为x元, B类实验器材每套的售价为y元,根据题意得,
,
解得
答:A、B两类实验器材每套的价格分别为300元、400元.
(2)解:设购A类实验器材m套,费用为W元,则,
∴.
∵
∴当时,W有最小值,最小值为10000元.
∴购进A类实验器材20套,B类实验器材10套时,总费用最低,最低费用为10000元.
22.(1)证明:延长和交于点M,
∵四边形是正方形,
∴,
∴,
∵点E是的中点,
∴,
又∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∴;
(2)
(3);
23.(1)解:∵二次函数的图象经过点,,
∴,
∴,
解得:,
∴二次函数解析式为,即.
当,,
∴,
一次函数过点和,
代入,得,解得,
∴一次函数解析式为;
(2)解:依题意,可设,则,
过点作于点,
∵是以为底边的等腰三角形,
∴,轴,
∴的纵坐标为2,
∴,
即有,
解得:(舍去)或,
∴.
(3)解:∵面积为,面积为,
∴,
如图,过作轴交于,而直线轴,
∴轴,则,
∴,
∴,
∵,直线为,
∴,,即,
∴,
∵,,
∴,
∴,
∵点是直线上方二次函数图象上的一个动点,
∴,
而,则有最大值,
当时,的最大值为:.
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.中国人很早开始使用负数,中国古代数学著作《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果支出1000元记作元,那么元表示( )
A.支出80元 B.收入 80元 C.支出1080元 D.收入1080元
2.如图,在下面四种用相同的正方体储物箱堆放在一起的形态中,从正面看到的和从左面看到的图形不相同的是( )
A. B.
C. D.
3.2025年1月17日上午,国家统计局发布数据,2024年全年出生人口约为9540000人,9540000用科学记数法表示为( )
A. B. C. D.
4.如图,将一副三角尺按图中所示位置摆放,点在的延长线上,点、分别为直角顶点,且,,若,则的度数是( )
A. B. C. D.
5.不等式组的解集在数轴上表示正确的是( )
A. B.
C. D.
6.估计的值应在 ( )
A.3和4之间 B.4和5之间 C.5和6之间 D.6和7之间
7.反比例函数y=的图象在( )
A.第一、三象限 B.第一、二象限
C.第二、四象限 D.第三、四象限
8.我们将如图所示的两种排列形式的点的个数分别称作“三角形数”(如1,3,6,10,…)和“正方形数”(如1,4,9,16,…),在小于200的数中,设最大的“三角形数”为m,最大的“正方形数”为n,则m+n的值为( )
A.33 B.301 C.386 D.571
9.如图,在△ABC中,∠C=90°,∠B=15°,AC=l,分别以点A,B为圆心,大于AB的长为半径画弧,两弧相交于点M,N,作直线MN交BC于点D,连接AD,则AD的长为( )
A.l.5 B. C.2 D.
10.已知某二次函数的图象如图所示,则这个二次函数的解析式为( )
A.y=﹣3(x﹣1)2+3 B.y=3(x﹣1)2+3
C.y=﹣3(x+1)2+3 D.y=3(x+1)2+3
二、填空题:本大题共5小题,每小题3分,共15分.
11.若实数x、y满足,则的值是 .
12.某正多边形的一个外角与一个内角的比为,则这个多边形是正 边形.
13.一个不透明的袋子中有4个白球,2个红球和a个黑球,它们除颜色外其余都相同,从中随机摸一个球,摸到黑球的概率为,则a的值为 .
14.如图,为半圆O的直径,将半圆O绕点A逆时针旋转,使点O的对应点恰好落在弧上,点为点B的对应点,连结.若,则阴影部分的面积为 (结果保留)
15.如图,已知正方形,点E在边上,,,连接,点F在射线上,且满足,那么 .
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.(1)分解因式:;
(2)解方程:
(3)解不等式组:
17.如图,已知四边形为平行四边形,,为对角线上的两点,且,连接,.
求证:.
18.国家航天局消息:北京时间2021年10月14日,神舟十三号成功发射,某中学科技兴趣小组为了解本校学生对航天科技的关注程度,在该校内进行了随机调查统计,将调查结果分为不关注、关注、比较关注、非常关注四类,回收、整理好全部调查问卷后,得到下列不完整的统计图:
(1)此次调查中接受调查的人数为______人;
(2)补全条形统计图,在扇形统计图中,“关注”对应扇形的圆心角为______;
(3)该校共有1200人,根据调查结果估计该校“关注”,“比较关注”及“非常关注”航天科技的人数共多少人?
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,在矩形中,为边上一点,连结.若,过点作于点.
(1)求证:.
(2)若,,求的长.
20.如图1是汽车内常备的千斤顶,图2是它的平面示意图,四边形是菱形,中间通过螺杆连接,转动手柄可改变线段的长度,同时改变的大小(菱形的边长不变),从而改变千斤顶的高度(即点与点之间的距离).经测量,.
(1)当时,求的长(结果保留整数).
(2)从增加到时,这个千斤顶高度升高了______cm(结果保留整数).(参考数据:,,)
21.我县初三实考在即,为了更好地备考,某校准备提前采购A、B两类实验器材.经查询,若购买A类实验器材2套和B类实验器材1套共需1000元;若购买A类实验器材2套和B类实验器材3套共需1800元.
(1)分别求出A、B两类实验器材每套的价格;
(2)经核算,该校决定共购买这两类实验器材30套,其中A类实验器材的数量不多于B类实验器材数量的2倍.如何购买才能使总费用最低?最低费用是多少元?
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.在一次数学活动课上,小明尝试着把一块含有的直角三角板放置于四边形的内部,且使得直角顶点E始终与边的中点重合,进行了一系列活动探究.
(1)【初步探究】
当四边形是正方形,顶点F、G分别在、边上,小明作辅助线“延长和交于点M”,证明了,请你补全证明过程.
(2)【类比探究】
如图2,当四边形是矩形,顶点F与A重合,点G在边上,类比图1的方法,不难求得______,______,请说明理由.
(3)【拓展探究】
当四边形是平行四边形,且.
如图3,当顶点F与A点重合,G在边上,则______;(直接写出答案,不需要说明理由)
如图4,当顶点F与D点重合,G在边上,则______.(直接写出答案,不需要说明理由)
23.如图,二次函数的图象与轴交于、两点,与轴交于点,一次函数经过点、、.点是直线上方二次函数图象上的一个动点,过点作直线轴于点,交直线于点,连接.
(1)求二次函数和一次函数的解析式;
(2)当是以为底边的等腰三角形时,求点的坐标;
(3)连接,连接交于点,记面积为,面积为,在点运动的过程中,判断是否存在最大值,若存在,求出其最大值,若不存在,请说明理由.
参考答案
1.D
2.D
3.C
4.A
5.B
6.D
7.A
8.C
9.C
10.A
11.2025
12.六
13.4
14.
15.2或14
16.解:(1)
;
(2)
整理,可得,
方程左右两边同时乘以可得:
,
解得,
检验:当时,
∴原分式方程的解为;
(3),
解不等式①,可得,
解不等式②,可得,
∴不等式组的解集为.
17.证明:四边形是平行四边形,
,,
,
∵,
∴,即,
在和中
,
,
.
18.(1)50
(2)
(3)1104
19.(1)证明:∵四边形是矩形,∴,,,
∴,
∵,
∴,
∴,
在与中,
,
∴;
(2)解:∵,∴设,,
∴,
∴,
∵,,
∴,
解得,
∴.
20.(1)的长约为
(2)13
21.(1)解:设A类实验器材每套的售价为x元, B类实验器材每套的售价为y元,根据题意得,
,
解得
答:A、B两类实验器材每套的价格分别为300元、400元.
(2)解:设购A类实验器材m套,费用为W元,则,
∴.
∵
∴当时,W有最小值,最小值为10000元.
∴购进A类实验器材20套,B类实验器材10套时,总费用最低,最低费用为10000元.
22.(1)证明:延长和交于点M,
∵四边形是正方形,
∴,
∴,
∵点E是的中点,
∴,
又∵,
∴,
∴,
∵,
∴垂直平分,
∴,
∴;
(2)
(3);
23.(1)解:∵二次函数的图象经过点,,
∴,
∴,
解得:,
∴二次函数解析式为,即.
当,,
∴,
一次函数过点和,
代入,得,解得,
∴一次函数解析式为;
(2)解:依题意,可设,则,
过点作于点,
∵是以为底边的等腰三角形,
∴,轴,
∴的纵坐标为2,
∴,
即有,
解得:(舍去)或,
∴.
(3)解:∵面积为,面积为,
∴,
如图,过作轴交于,而直线轴,
∴轴,则,
∴,
∴,
∵,直线为,
∴,,即,
∴,
∵,,
∴,
∴,
∵点是直线上方二次函数图象上的一个动点,
∴,
而,则有最大值,
当时,的最大值为:.
同课章节目录
