2024-2025六年级下册数学期末综合复习题(试题)苏教版(含答案)
文档属性
| 名称 | 2024-2025六年级下册数学期末综合复习题(试题)苏教版(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 319.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 14:38:29 | ||
图片预览




文档简介
2024-2025六年级下册数学期末综合复习题(试题)苏教版(含答案)
一、单选题
1.等底等高的圆锥、正方体、长方体相比较, ( )的体积最小。
A.圆锥 B.正方体 C.长方体
2.一件商品打六折出售,下面( )关系式错误的。
A.现价=原价×60%
B.降低的价格=原价×(1﹣60%)
C.原价=现价×(1﹣60%)
D.现价÷原价=60%
3.袋子里有5个红球、3个黄球、1个白球,任意摸出一个球,摸到( )球的可能性最小。
A.红 B.黄 C.白
4.一根长方体木料长3米,宽和高都是3分米,把它锯成5段,表面积最少增加( )。
A.27平方分米 B.36平方分米 C.45平方分米 D.72平方分米
5.把下图所示长方形纸卷成圆柱形(接口处忽略不计),所得圆柱的高是10cm,它的底面直径是( )cm。
A.5 B.10 C.31.4 D.3
6.跳绳兴趣班的学生分组跳绳,可以分成5人一组,也可以分成6人一组,都正好分完。如果这个兴趣班的总人数在40人以内,可能是( )。
A.11人 B.33人 C.30人 D.38人
7.将3个相同的正方体放在墙角处,露在外面的面积的变化有( )种。
A.1种 B.3种 C.4种
8.一个长方体的上面、右面和前面的面积分别是24平方厘米、30平方厘米、20平方厘米,这个长方体的体积是( )立方厘米。
A.120 B.600 C.720
二、判断题
9.扇形统计图可以直观的表示部分数量与总数之间的关系。( )
10.某小学篮球队队员的平均身高是162厘米,那么这个篮球队所有队员的身高一定都不低于162厘米。( )
11.四(2)班垃圾分类知识答题比赛中的平均分是87分,就是每个同学实际都得了87分。( )
12.长方体、正方体、圆柱的体积都可以用底面积乘高来计算。( )
13.长方体、正方体和圆锥的体积公式都可以用V=Sh 表示。( )
14.支出500元和收入1000 元是一对具有相反意义的量。( )
15.分别绕下面直角三角形的两条直角边旋转,得到的两个圆锥的体积相等。( )
三、填空题
16.如果3a=5b,那么a∶b= ∶ 。
17.一列高铁上午9:20出发,下午2:20到达终点站。列车在运行过程中平均时速是300千米,这列车一共行驶 千米。解决这个问题,所用的数量关系式是 。
18.妈妈用电饭煲煲粥,晚上9:00开始预约,要想第二天早上6:00煲好粥,需要预约 小时。(此款电饭煲的“预约时间”是指从开始预约到烹饪完成的时长)
19.把三个棱长1米的正方体拼成一个长方体(如图),拼成的长方体的表面积是 平方米,体积是 立方米。
20.一个圆的周长是12.56厘米,这个圆的半径是 ,面积是 。
21.等底等高的圆柱和圆锥,它们的体积之差是12立方分米。圆柱的体积是 立方分米。
22.小区停车场里停了汽车和三轮摩托车共24辆,共有轮子92个,三轮摩托有 辆,汽车有 辆。
23.一个圆柱形状的易拉罐,底面直径7厘米,高10厘米.做这样一个易拉罐,至少需要 平方厘米的合金材料
四、口算与估算
24.直接写出得数。
2.5×0.4= 6.3÷9= 7.6+0.6= 10.5-5=
200×0.5= 57÷1.9= 4÷80= 0.45÷0.3=
1.29-1.29÷1.29=
五、竖式计算
25.列竖式计算,带*的要验算。
0.28×0.08= *3.45×8.6=
8.06×6.2= *63.5×0.14=
六、脱式计算
26. 递等式计算,能简算的要简算。
1.25×8÷1.25×8 1.95÷(3.58-2.8) 1.84÷0.23 +2.76÷0.23
七、解方程
27.解方程。
①x+36=100
②0.3x+3.2×5=22
③0.35:=x:6
八、操作题
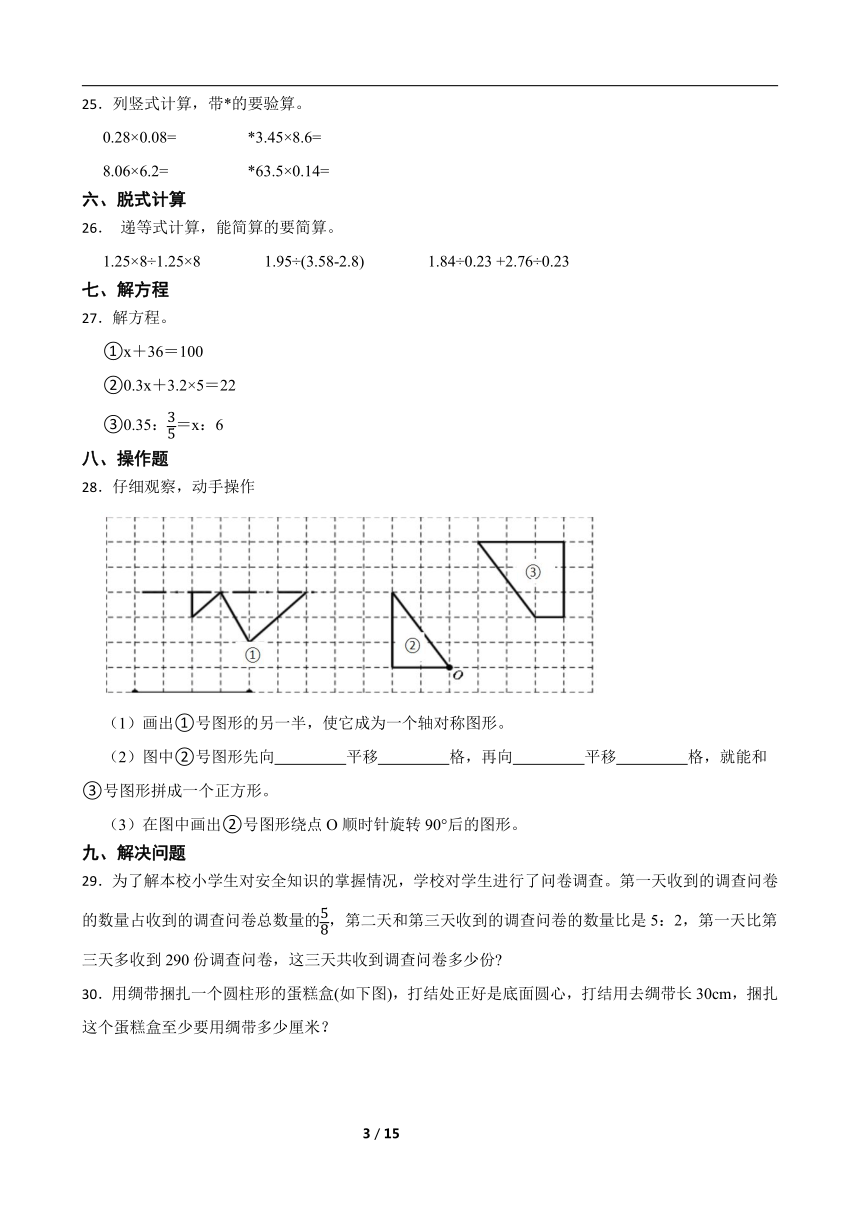
28.仔细观察,动手操作
(1)画出①号图形的另一半,使它成为一个轴对称图形。
(2)图中②号图形先向 平移 格,再向 平移 格,就能和③号图形拼成一个正方形。
(3)在图中画出②号图形绕点O顺时针旋转90°后的图形。
九、解决问题
29.为了解本校小学生对安全知识的掌握情况,学校对学生进行了问卷调查。第一天收到的调查问卷的数量占收到的调查问卷总数量的,第二天和第三天收到的调查问卷的数量比是5:2,第一天比第三天多收到290份调查问卷,这三天共收到调查问卷多少份
30.用绸带捆扎一个圆柱形的蛋糕盒(如下图),打结处正好是底面圆心,打结用去绸带长30cm,捆扎这个蛋糕盒至少要用绸带多少厘米?
31.向阳小学为希望小学捐书,捐赠故事书240本,是科技书的3.2倍。捐赠的科技书比故事书少多少本?
32.公园里有一个周长12.56米的圆形花坛。
(1)这个花坛的占地面积是多少?
(2)公园要在花坛的四周铺一条1米宽的小路,这条小路的面积是多少?
33.在一片草地正中拴着一头牛,绳长6米,这头牛最多可吃到的青草的面积是多少?
34.青年旅行社推出“北京美景一日游”的两种出游方案。
方案一:成人每人240元,儿童每人120元
方案二:团体6人以上(包括6人),每人150元
(1)成人4人,儿童2人,选哪种方案合算
(2)成人1人,儿童5人,选哪种方案合算
35.小华把一条彩带一段一段剪成了都是6厘米的小段,一共剪了4次。这条彩带原来长多少厘米?
36.周末了,同学们相约去爬山,从山脚到达山顶大约2.85千米。他们上山用了2.5时,沿原路下山用时比上少1时。
(1)他们下山时的平均速度是每时多少千米?
(2)上山时的平均速度比下山时的平均速度慢多少千米?
(3)在整个爬山过程中,他们的平均速度是每时多少千米?
答案解析部分
1.【答案】A
【解析】【解答】解:设圆锥、正方体、长方体的底面积分别为S,高为h。
圆锥的体积=Sh,正方体的体积=Sh,长方体的体积=Sh,Sh故答案为:A。
【分析】圆锥的体积=底面积×高×,正方体的体积=底面积×高,长方体的体积=底面积×高;因此,当三者底面积和高相等时,圆锥的体积只是正方体或长方体体积的,所以圆锥的体积最小。
2.【答案】C
【解析】【解答】解:一件商品打六折出售,原价=现价×(1﹣60%)这个关系错误。
故答案为:C。
【分析】六折就是60%;现价=原价×60%,据此列式作答即可。
3.【答案】C
【解析】【解答】因为1<3<5,所以任意摸出一个球,摸到白球的可能性最小。
故答案为:C。
【分析】可能性的大小与物体数量的多少有关,哪种颜色的球数量越少,摸到的可能性越小,据此解答。
4.【答案】D
5.【答案】B
【解析】【解答】解:31.4÷31.4=10(厘米)
故答案:B。
【分析】根据题意分析可知,这个长方形的长是圆柱的底面周长,宽是圆柱的高,由周长公式C=πd,即可解答。
6.【答案】C
【解析】【解答】解:5×6=30(人)
故答案为:C。
【分析】这个兴趣班的总人数在40人以内,并且同时是5和6的倍数,总人数=5×6=30人。
7.【答案】A
【解析】【解答】通过想象可知,将3个相同的正方体放在墙角处,有两种摆放方法,露出的面积都是7个面。即露在外面的面积的变化有1种。
故答案为:A。
【分析】第一种:露在外面的面积有7个面;
第二种:露在外面的面积有7个面;
8.【答案】A
【解析】【解答】24=4×6,30=5×6,20=4×5,则这个长方体的长、宽、高分别为4cm,6cm,5cm,体积为4×6×5=120(cm3)。
故答案为:A
【分析】长方体上面是长方体的长乘宽得到的;前面的面积是长方体的长乘高得到的,右面是长方体的宽乘高得到的,根据这三个面的面积判断出长方体的长宽高,再根据长方体体积公式计算体积即可。
9.【答案】正确
【解析】【解答】解:扇形统计图可以直观的表示部分数量与总数之间的关系。
故答案为:正确。
【分析】根据扇形统计图的特征作答即可。
10.【答案】错误
11.【答案】错误
【解析】【解答】解:平均分是87分,则有人成绩可能比87分高,也有可能比87分低,也有可能正好是87分,原题说法错误。
故答案为:错误。
【分析】一组数据的和÷这组数据的个数=这组数据的平均数。
12.【答案】正确
【解析】【解答】解:长方体、正方体、圆柱的体积都可以用底面积乘高来计算。
故答案为:正确。
【分析】根据长方体、正方体、圆柱的体积的计算方法作答即可。
13.【答案】错误
【解析】【解答】解: 长方体和正方体的体积计算公式都可以用表示,而圆锥的体积计算公式是,不能用表示,所以原说法错误。
故答案为:错误
【分析】长方体和正方体的体积计算公式都可以用表示,其中S是底面积,h是高。圆锥的体积计算公式是,这与长方体和正方体的公式不同。据此解答。
14.【答案】正确
【解析】【解答】解:支出500元和收入1000 元是一对具有相反意义的量
故答案为:正确。
【分析】相反意义的量是指两个量的意义相反,并且可以用正负数表示。支出表示资金流出,收入表示资金流入,故支出500元和收入1000 元是一对具有相反意义的量。
15.【答案】错误
16.【答案】5;3
【解析】【解答】 如果3a=5b,那么a:b=5:3.
故答案为:5;3.
【分析】根据比例的基本性质可知,相乘的两个数同时作外项或内项,题中的a为一个外项,则3为另一个外项,b为一个内项,则5为另一个内项,据此解答即可.
17.【答案】1500;速度×时间=路程
【解析】【解答】解:下午2:20是14:20,
14:20-9:20=5小时
300×5=1500(千米)
所用的数量关系式是速度×时间=路程。
故答案为:1500;速度×时间=路程。
【分析】300是速度,5小时是时间,速度×时间=路程。
18.【答案】9
【解析】【解答】解:晚上9时是21时,早上6时是6时;
24时-21时+6时=9小时。
故答案为:9。
【分析】普通计时法转化成24时计时法的方法:中午12时以前的,直接去掉限制词,12时以后的,去掉限制词,加上12;一天是24小时,要求预约时间,分两段计算,先求出当天晚上预约的时间,再加上第二天预约的时间,据此列式解答。
19.【答案】14;3
【解析】【解答】解:表面积:
(3×1+1×1+3×1)×2
=7×2
=14(平方米)
体积:3×1×1=3(立方米)
故答案为:14;3。
【分析】拼成后的长方体的长是1+1+1=3米,宽是1米,高是1米。长方体表面积=(长×宽+长×高+宽×高)×2,体积=长×宽×高。
20.【答案】2厘米;12.56平方厘米
【解析】【解答】解:12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)。
故答案为:2厘米;12.56平方厘米。
【分析】这个圆的半径=周长÷π÷2,这个圆的面积=π×半径2。
21.【答案】18
【解析】【解答】解:12÷2×3
=6×3
=18(立方分米)。
故答案为:18。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆柱的体积=圆柱和圆锥的体积之差÷2×3。
22.【答案】4;20
【解析】【解答】可以画图也可以画表来分析:
结论:三轮摩托车有4辆,汽车有20辆.
故答案为:4;20
【分析】鸡兔同笼的问题可以用列表的方法解答,先确定汽车的辆数是24辆,计算出轮子数,然后减少汽车的辆数,增加摩托车辆数,直到轮子数是92即可判断出两种车的辆数.
23.【答案】296.73
【解析】【解答】3.14×7×10+2×3.14×(7÷2)2
=3.14×7×10+2×3.14×12.25
=21.98×10+6.28×12.25
=219.8+76.93
=296.73(平方厘米)
故答案为:296.73
【分析】已知圆柱的底面直径d和高h,求表面积S,用公式:S=πdh+2π(d÷2)2,据此列式解答.
24.【答案】
2.5×0.4=1 6.3÷9=0.7 7.6+0.6=8.2 10.5-5=5.5
200×0.5=100 57÷1.9=30 4÷80=0.05 0.45÷0.3=1.5
1.29-1.29÷1.29=0.29
【解析】【分析】小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
除数是整数的小数除法计算法则:先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添“0”,再继续除;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个算式中有除法和减法,先算除法,后算减法。
25.【答案】解:(1)0.28×0.08
=
(2)8.06×6.2
=
(3)3.45×8.6
=
验算:
(4)63.5×0.14
验算:
【解析】【分析】本题运用小数乘法的竖式的计算方法进行计算即可.
26.【答案】解:1.25×8÷1.25×8
=(1.25÷1.25)×(8×8)
=1×64
=64
1.95÷(3.58-2.8)
=1.95÷0.78
=2.5
1.84÷0.23 +2.76÷0.23
=(1.84+2.76)÷0.23
=4.6÷0.23
=20
【解析】【分析】先计算(1.25÷1.25)和(8×8),然后再相乘;也可以按照从左到右的顺序计算;
先算括号里面的减法,再算括号外面的除法;
先计算(1.84+2.76)=4.6,然后再除以0.23。
27.【答案】①x+36=100
解: x=100-36
x=64
②0.3x+3.2×5=22
解:0.3x+16=22
0.3x=6
x=6÷0.3
x=20
③0.35:=x:6
解: x=0.35×6
x=2.1
x=2.1÷
x=3.5
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①应用等式的性质1解方程;
②综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积;
③应用比例的基本性质解比例。
28.【答案】(1)解:
(2)上;2;右;3
(3)解:
【解析】【解答】解:(2)图中②号图形先向上平移2格,再向右平移3格,就能和③号图形拼成一个正方形。
故答案为:(2)上;2;右;3。(答案不唯一)
【分析】(1)轴对称图形对应点到对称轴的距离相等,先确定对应点的位置,再画出轴对称图形的另一半;
(2)先观察②和③的特征,然后确定平移的方向,根据对应点之间的格数确定平移的格数;
(3)先确定旋转中心,然后根据旋转方向和度数确定对应点的位置,再画出旋转后的图形。
29.【答案】解:第三天收到的调查问卷的数量占调查问卷总数量的
收到的调查问卷总数量为(份)
答:这三天共收到调查问卷 560份。
【解析】【分析】先根据第一天收到问卷占比求出第三天收到问卷占比,即,再利用第一天比第三天多收290份这一条件,用多的份数除以第一天与第三天占比之差,得出问卷总数。
30.【答案】解:40×4+20×4+30
=240+30
=270(厘米)
答:捆扎这个蛋糕盒至少要用绸带270厘米。
【解析】【分析】根据题意及看图可知绸带由三部分组成:4条底面直径、4条高和打结的地方,因此,直径×4+高×4+打结用去的长度=需要的绸带长度。
31.【答案】解:240-240÷3.2
=240-75
=165(本)
答:捐赠的科技书比故事书少165本。
【解析】【分析】捐赠故事书的本数÷3.2=捐赠科技书的本数,捐赠故事书的本数-捐赠科技书的本数=捐赠的科技书比故事书少的本数。
32.【答案】(1)12.56平方米
(2)15.7平方米
33.【答案】解:3.14×62
=3.14×36
=113.04(平方米)
答:这头牛最多可吃到的青草的面积是113.04平方米。
【解析】【分析】这头牛最多可吃到青草的面积=π×半径2,其中,半径=绳子的长。
34.【答案】(1)解:方案一:240×4+120×2
=960+240
=1200(元)
方案二:150×(4+2)
=150×6
=900(元)
1200元>900元
答:方案二合算。
(2)解:方案一:240+120×5
=240+600
=840(元)
方案二:150×(4+2)
=150×6
=900(元)
900元>840元
答:方案一合算。
【解析】【分析】分别算出每种方案花费的钱数,比较大小后,选择最优方案。
35.【答案】6×(4+1)
=6×5
=30(厘米)
答:这条彩带原来长30厘米。
【解析】【分析】剪1次会剪出2段,剪4次会剪出5段,因此用每段的长度乘剪的段数即可求出彩带原来的长度。
36.【答案】(1)解:2.85÷(2.5-1)
=2.85÷1.5
=1.9(千米)
答:他们下山时的平均速度是每时4.75千米。
(2)解:1.9-2.85÷2.5
=1.9-1.14
=0.76(千米)
答:上山时的平均速度比下山时的平均速度慢0.76千米。
(3)解:(2.85+2.85)÷(2.5+1.5)
=5.7÷4
=1.425(千米)
答:他们的平均速度是每时1.425千米。
【解析】【分析】(1)上山时间-1=下山时间,路程÷下山时间=下山速度;
(2)路程÷上山时间=上山速度,下山速度-上山速度=上山下山的速度差;
(3)上山下山的总路程÷总时间=上山下山的平均速度。
1 / 1
一、单选题
1.等底等高的圆锥、正方体、长方体相比较, ( )的体积最小。
A.圆锥 B.正方体 C.长方体
2.一件商品打六折出售,下面( )关系式错误的。
A.现价=原价×60%
B.降低的价格=原价×(1﹣60%)
C.原价=现价×(1﹣60%)
D.现价÷原价=60%
3.袋子里有5个红球、3个黄球、1个白球,任意摸出一个球,摸到( )球的可能性最小。
A.红 B.黄 C.白
4.一根长方体木料长3米,宽和高都是3分米,把它锯成5段,表面积最少增加( )。
A.27平方分米 B.36平方分米 C.45平方分米 D.72平方分米
5.把下图所示长方形纸卷成圆柱形(接口处忽略不计),所得圆柱的高是10cm,它的底面直径是( )cm。
A.5 B.10 C.31.4 D.3
6.跳绳兴趣班的学生分组跳绳,可以分成5人一组,也可以分成6人一组,都正好分完。如果这个兴趣班的总人数在40人以内,可能是( )。
A.11人 B.33人 C.30人 D.38人
7.将3个相同的正方体放在墙角处,露在外面的面积的变化有( )种。
A.1种 B.3种 C.4种
8.一个长方体的上面、右面和前面的面积分别是24平方厘米、30平方厘米、20平方厘米,这个长方体的体积是( )立方厘米。
A.120 B.600 C.720
二、判断题
9.扇形统计图可以直观的表示部分数量与总数之间的关系。( )
10.某小学篮球队队员的平均身高是162厘米,那么这个篮球队所有队员的身高一定都不低于162厘米。( )
11.四(2)班垃圾分类知识答题比赛中的平均分是87分,就是每个同学实际都得了87分。( )
12.长方体、正方体、圆柱的体积都可以用底面积乘高来计算。( )
13.长方体、正方体和圆锥的体积公式都可以用V=Sh 表示。( )
14.支出500元和收入1000 元是一对具有相反意义的量。( )
15.分别绕下面直角三角形的两条直角边旋转,得到的两个圆锥的体积相等。( )
三、填空题
16.如果3a=5b,那么a∶b= ∶ 。
17.一列高铁上午9:20出发,下午2:20到达终点站。列车在运行过程中平均时速是300千米,这列车一共行驶 千米。解决这个问题,所用的数量关系式是 。
18.妈妈用电饭煲煲粥,晚上9:00开始预约,要想第二天早上6:00煲好粥,需要预约 小时。(此款电饭煲的“预约时间”是指从开始预约到烹饪完成的时长)
19.把三个棱长1米的正方体拼成一个长方体(如图),拼成的长方体的表面积是 平方米,体积是 立方米。
20.一个圆的周长是12.56厘米,这个圆的半径是 ,面积是 。
21.等底等高的圆柱和圆锥,它们的体积之差是12立方分米。圆柱的体积是 立方分米。
22.小区停车场里停了汽车和三轮摩托车共24辆,共有轮子92个,三轮摩托有 辆,汽车有 辆。
23.一个圆柱形状的易拉罐,底面直径7厘米,高10厘米.做这样一个易拉罐,至少需要 平方厘米的合金材料
四、口算与估算
24.直接写出得数。
2.5×0.4= 6.3÷9= 7.6+0.6= 10.5-5=
200×0.5= 57÷1.9= 4÷80= 0.45÷0.3=
1.29-1.29÷1.29=
五、竖式计算
25.列竖式计算,带*的要验算。
0.28×0.08= *3.45×8.6=
8.06×6.2= *63.5×0.14=
六、脱式计算
26. 递等式计算,能简算的要简算。
1.25×8÷1.25×8 1.95÷(3.58-2.8) 1.84÷0.23 +2.76÷0.23
七、解方程
27.解方程。
①x+36=100
②0.3x+3.2×5=22
③0.35:=x:6
八、操作题
28.仔细观察,动手操作
(1)画出①号图形的另一半,使它成为一个轴对称图形。
(2)图中②号图形先向 平移 格,再向 平移 格,就能和③号图形拼成一个正方形。
(3)在图中画出②号图形绕点O顺时针旋转90°后的图形。
九、解决问题
29.为了解本校小学生对安全知识的掌握情况,学校对学生进行了问卷调查。第一天收到的调查问卷的数量占收到的调查问卷总数量的,第二天和第三天收到的调查问卷的数量比是5:2,第一天比第三天多收到290份调查问卷,这三天共收到调查问卷多少份
30.用绸带捆扎一个圆柱形的蛋糕盒(如下图),打结处正好是底面圆心,打结用去绸带长30cm,捆扎这个蛋糕盒至少要用绸带多少厘米?
31.向阳小学为希望小学捐书,捐赠故事书240本,是科技书的3.2倍。捐赠的科技书比故事书少多少本?
32.公园里有一个周长12.56米的圆形花坛。
(1)这个花坛的占地面积是多少?
(2)公园要在花坛的四周铺一条1米宽的小路,这条小路的面积是多少?
33.在一片草地正中拴着一头牛,绳长6米,这头牛最多可吃到的青草的面积是多少?
34.青年旅行社推出“北京美景一日游”的两种出游方案。
方案一:成人每人240元,儿童每人120元
方案二:团体6人以上(包括6人),每人150元
(1)成人4人,儿童2人,选哪种方案合算
(2)成人1人,儿童5人,选哪种方案合算
35.小华把一条彩带一段一段剪成了都是6厘米的小段,一共剪了4次。这条彩带原来长多少厘米?
36.周末了,同学们相约去爬山,从山脚到达山顶大约2.85千米。他们上山用了2.5时,沿原路下山用时比上少1时。
(1)他们下山时的平均速度是每时多少千米?
(2)上山时的平均速度比下山时的平均速度慢多少千米?
(3)在整个爬山过程中,他们的平均速度是每时多少千米?
答案解析部分
1.【答案】A
【解析】【解答】解:设圆锥、正方体、长方体的底面积分别为S,高为h。
圆锥的体积=Sh,正方体的体积=Sh,长方体的体积=Sh,Sh
【分析】圆锥的体积=底面积×高×,正方体的体积=底面积×高,长方体的体积=底面积×高;因此,当三者底面积和高相等时,圆锥的体积只是正方体或长方体体积的,所以圆锥的体积最小。
2.【答案】C
【解析】【解答】解:一件商品打六折出售,原价=现价×(1﹣60%)这个关系错误。
故答案为:C。
【分析】六折就是60%;现价=原价×60%,据此列式作答即可。
3.【答案】C
【解析】【解答】因为1<3<5,所以任意摸出一个球,摸到白球的可能性最小。
故答案为:C。
【分析】可能性的大小与物体数量的多少有关,哪种颜色的球数量越少,摸到的可能性越小,据此解答。
4.【答案】D
5.【答案】B
【解析】【解答】解:31.4÷31.4=10(厘米)
故答案:B。
【分析】根据题意分析可知,这个长方形的长是圆柱的底面周长,宽是圆柱的高,由周长公式C=πd,即可解答。
6.【答案】C
【解析】【解答】解:5×6=30(人)
故答案为:C。
【分析】这个兴趣班的总人数在40人以内,并且同时是5和6的倍数,总人数=5×6=30人。
7.【答案】A
【解析】【解答】通过想象可知,将3个相同的正方体放在墙角处,有两种摆放方法,露出的面积都是7个面。即露在外面的面积的变化有1种。
故答案为:A。
【分析】第一种:露在外面的面积有7个面;
第二种:露在外面的面积有7个面;
8.【答案】A
【解析】【解答】24=4×6,30=5×6,20=4×5,则这个长方体的长、宽、高分别为4cm,6cm,5cm,体积为4×6×5=120(cm3)。
故答案为:A
【分析】长方体上面是长方体的长乘宽得到的;前面的面积是长方体的长乘高得到的,右面是长方体的宽乘高得到的,根据这三个面的面积判断出长方体的长宽高,再根据长方体体积公式计算体积即可。
9.【答案】正确
【解析】【解答】解:扇形统计图可以直观的表示部分数量与总数之间的关系。
故答案为:正确。
【分析】根据扇形统计图的特征作答即可。
10.【答案】错误
11.【答案】错误
【解析】【解答】解:平均分是87分,则有人成绩可能比87分高,也有可能比87分低,也有可能正好是87分,原题说法错误。
故答案为:错误。
【分析】一组数据的和÷这组数据的个数=这组数据的平均数。
12.【答案】正确
【解析】【解答】解:长方体、正方体、圆柱的体积都可以用底面积乘高来计算。
故答案为:正确。
【分析】根据长方体、正方体、圆柱的体积的计算方法作答即可。
13.【答案】错误
【解析】【解答】解: 长方体和正方体的体积计算公式都可以用表示,而圆锥的体积计算公式是,不能用表示,所以原说法错误。
故答案为:错误
【分析】长方体和正方体的体积计算公式都可以用表示,其中S是底面积,h是高。圆锥的体积计算公式是,这与长方体和正方体的公式不同。据此解答。
14.【答案】正确
【解析】【解答】解:支出500元和收入1000 元是一对具有相反意义的量
故答案为:正确。
【分析】相反意义的量是指两个量的意义相反,并且可以用正负数表示。支出表示资金流出,收入表示资金流入,故支出500元和收入1000 元是一对具有相反意义的量。
15.【答案】错误
16.【答案】5;3
【解析】【解答】 如果3a=5b,那么a:b=5:3.
故答案为:5;3.
【分析】根据比例的基本性质可知,相乘的两个数同时作外项或内项,题中的a为一个外项,则3为另一个外项,b为一个内项,则5为另一个内项,据此解答即可.
17.【答案】1500;速度×时间=路程
【解析】【解答】解:下午2:20是14:20,
14:20-9:20=5小时
300×5=1500(千米)
所用的数量关系式是速度×时间=路程。
故答案为:1500;速度×时间=路程。
【分析】300是速度,5小时是时间,速度×时间=路程。
18.【答案】9
【解析】【解答】解:晚上9时是21时,早上6时是6时;
24时-21时+6时=9小时。
故答案为:9。
【分析】普通计时法转化成24时计时法的方法:中午12时以前的,直接去掉限制词,12时以后的,去掉限制词,加上12;一天是24小时,要求预约时间,分两段计算,先求出当天晚上预约的时间,再加上第二天预约的时间,据此列式解答。
19.【答案】14;3
【解析】【解答】解:表面积:
(3×1+1×1+3×1)×2
=7×2
=14(平方米)
体积:3×1×1=3(立方米)
故答案为:14;3。
【分析】拼成后的长方体的长是1+1+1=3米,宽是1米,高是1米。长方体表面积=(长×宽+长×高+宽×高)×2,体积=长×宽×高。
20.【答案】2厘米;12.56平方厘米
【解析】【解答】解:12.56÷3.14÷2
=4÷2
=2(厘米)
3.14×22
=3.14×4
=12.56(平方厘米)。
故答案为:2厘米;12.56平方厘米。
【分析】这个圆的半径=周长÷π÷2,这个圆的面积=π×半径2。
21.【答案】18
【解析】【解答】解:12÷2×3
=6×3
=18(立方分米)。
故答案为:18。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,圆柱的体积=圆柱和圆锥的体积之差÷2×3。
22.【答案】4;20
【解析】【解答】可以画图也可以画表来分析:
结论:三轮摩托车有4辆,汽车有20辆.
故答案为:4;20
【分析】鸡兔同笼的问题可以用列表的方法解答,先确定汽车的辆数是24辆,计算出轮子数,然后减少汽车的辆数,增加摩托车辆数,直到轮子数是92即可判断出两种车的辆数.
23.【答案】296.73
【解析】【解答】3.14×7×10+2×3.14×(7÷2)2
=3.14×7×10+2×3.14×12.25
=21.98×10+6.28×12.25
=219.8+76.93
=296.73(平方厘米)
故答案为:296.73
【分析】已知圆柱的底面直径d和高h,求表面积S,用公式:S=πdh+2π(d÷2)2,据此列式解答.
24.【答案】
2.5×0.4=1 6.3÷9=0.7 7.6+0.6=8.2 10.5-5=5.5
200×0.5=100 57÷1.9=30 4÷80=0.05 0.45÷0.3=1.5
1.29-1.29÷1.29=0.29
【解析】【分析】小数乘法法则:先按照整数乘法的计算法则算出积,再看因数中共有几位小数,就从积的右边起数出几位,点上小数点;如果位数不够,就用“0”补足,注意:计算的结果,如果小数末尾有0的,根据小数的基本性质,在小数的末尾去掉零,小数的大小不变;
除数是整数的小数除法计算法则:先按照整数除法的法则去除,商的小数点要和被除数的小数点对齐;如果除到被除数的末尾仍有余数,就在余数后面添“0”,再继续除;
除数是小数的除法计算法则:先移动除数的小数点,使它变成整数,除数的小数点向右移动几位,被除数的小数点也向右移动几位(位数不够的补“0”),然后按照除数是整数的除法法则进行计算;
一个算式中有除法和减法,先算除法,后算减法。
25.【答案】解:(1)0.28×0.08
=
(2)8.06×6.2
=
(3)3.45×8.6
=
验算:
(4)63.5×0.14
验算:
【解析】【分析】本题运用小数乘法的竖式的计算方法进行计算即可.
26.【答案】解:1.25×8÷1.25×8
=(1.25÷1.25)×(8×8)
=1×64
=64
1.95÷(3.58-2.8)
=1.95÷0.78
=2.5
1.84÷0.23 +2.76÷0.23
=(1.84+2.76)÷0.23
=4.6÷0.23
=20
【解析】【分析】先计算(1.25÷1.25)和(8×8),然后再相乘;也可以按照从左到右的顺序计算;
先算括号里面的减法,再算括号外面的除法;
先计算(1.84+2.76)=4.6,然后再除以0.23。
27.【答案】①x+36=100
解: x=100-36
x=64
②0.3x+3.2×5=22
解:0.3x+16=22
0.3x=6
x=6÷0.3
x=20
③0.35:=x:6
解: x=0.35×6
x=2.1
x=2.1÷
x=3.5
【解析】【分析】等式的性质1:等式两边加上或减去同一个数,左右两边仍然相等;等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,左右两边仍然相等;
①应用等式的性质1解方程;
②综合应用等式的性质解方程;
比例的基本性质:在比例里,两个内项积等于两个外项积;
③应用比例的基本性质解比例。
28.【答案】(1)解:
(2)上;2;右;3
(3)解:
【解析】【解答】解:(2)图中②号图形先向上平移2格,再向右平移3格,就能和③号图形拼成一个正方形。
故答案为:(2)上;2;右;3。(答案不唯一)
【分析】(1)轴对称图形对应点到对称轴的距离相等,先确定对应点的位置,再画出轴对称图形的另一半;
(2)先观察②和③的特征,然后确定平移的方向,根据对应点之间的格数确定平移的格数;
(3)先确定旋转中心,然后根据旋转方向和度数确定对应点的位置,再画出旋转后的图形。
29.【答案】解:第三天收到的调查问卷的数量占调查问卷总数量的
收到的调查问卷总数量为(份)
答:这三天共收到调查问卷 560份。
【解析】【分析】先根据第一天收到问卷占比求出第三天收到问卷占比,即,再利用第一天比第三天多收290份这一条件,用多的份数除以第一天与第三天占比之差,得出问卷总数。
30.【答案】解:40×4+20×4+30
=240+30
=270(厘米)
答:捆扎这个蛋糕盒至少要用绸带270厘米。
【解析】【分析】根据题意及看图可知绸带由三部分组成:4条底面直径、4条高和打结的地方,因此,直径×4+高×4+打结用去的长度=需要的绸带长度。
31.【答案】解:240-240÷3.2
=240-75
=165(本)
答:捐赠的科技书比故事书少165本。
【解析】【分析】捐赠故事书的本数÷3.2=捐赠科技书的本数,捐赠故事书的本数-捐赠科技书的本数=捐赠的科技书比故事书少的本数。
32.【答案】(1)12.56平方米
(2)15.7平方米
33.【答案】解:3.14×62
=3.14×36
=113.04(平方米)
答:这头牛最多可吃到的青草的面积是113.04平方米。
【解析】【分析】这头牛最多可吃到青草的面积=π×半径2,其中,半径=绳子的长。
34.【答案】(1)解:方案一:240×4+120×2
=960+240
=1200(元)
方案二:150×(4+2)
=150×6
=900(元)
1200元>900元
答:方案二合算。
(2)解:方案一:240+120×5
=240+600
=840(元)
方案二:150×(4+2)
=150×6
=900(元)
900元>840元
答:方案一合算。
【解析】【分析】分别算出每种方案花费的钱数,比较大小后,选择最优方案。
35.【答案】6×(4+1)
=6×5
=30(厘米)
答:这条彩带原来长30厘米。
【解析】【分析】剪1次会剪出2段,剪4次会剪出5段,因此用每段的长度乘剪的段数即可求出彩带原来的长度。
36.【答案】(1)解:2.85÷(2.5-1)
=2.85÷1.5
=1.9(千米)
答:他们下山时的平均速度是每时4.75千米。
(2)解:1.9-2.85÷2.5
=1.9-1.14
=0.76(千米)
答:上山时的平均速度比下山时的平均速度慢0.76千米。
(3)解:(2.85+2.85)÷(2.5+1.5)
=5.7÷4
=1.425(千米)
答:他们的平均速度是每时1.425千米。
【解析】【分析】(1)上山时间-1=下山时间,路程÷下山时间=下山速度;
(2)路程÷上山时间=上山速度,下山速度-上山速度=上山下山的速度差;
(3)上山下山的总路程÷总时间=上山下山的平均速度。
1 / 1
同课章节目录
