多边形及其内角和
图片预览
文档简介
7.2.1三角形的内角
学习目标
1 经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2 能应用三角形内角和定理解决一些简单的实际问题
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
课前准备
每个学生准备好二个由硬纸片剪出的三角形
学习过程
1、 做一做
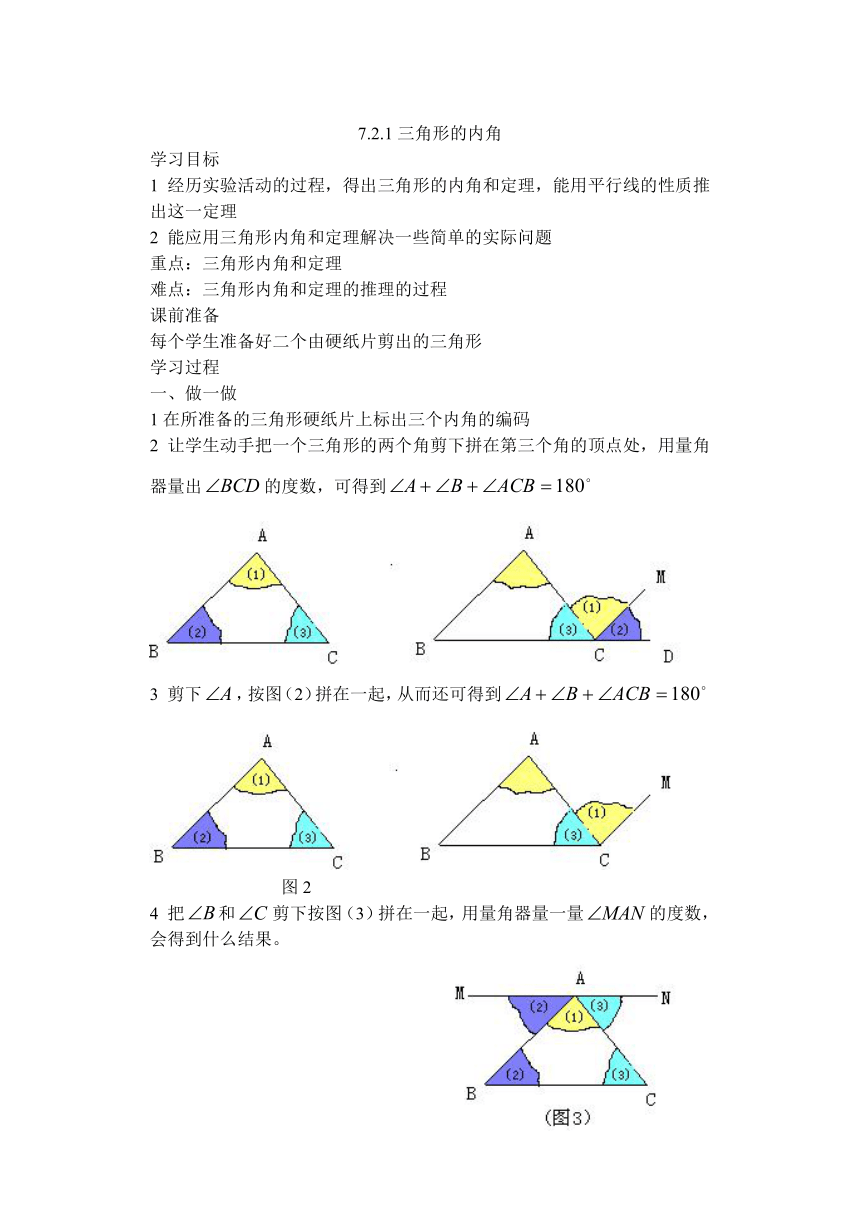
1在所准备的三角形硬纸片上标出三个内角的编码
2 让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
3 剪下,按图(2)拼在一起,从而还可得到
图2
4 把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。
二、想一想、做一做、学生展示
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
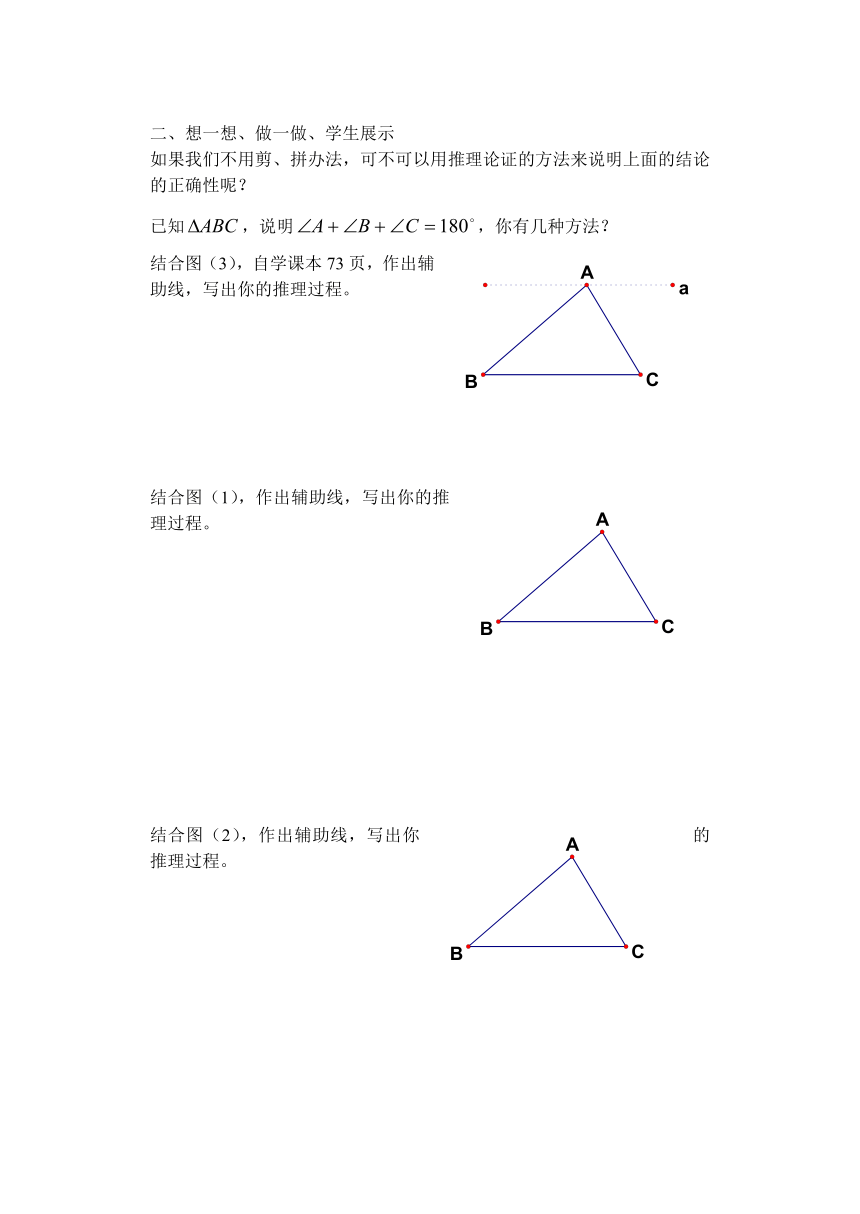
结合图(3),自学课本73页,作出辅助线,写出你的推理过程。
结合图(1),作出辅助线,写出你的推理过程。
结合图(2),作出辅助线,写出你的推理过程。
能不能用图(4)也可以说明这个结论成立
三角形内角和定理:_____________________________________。
例题:如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
你还能想出其它解法吗?
练习:
1、课本P74,练习1,2
2、课本76页习题7.2 1,2,3,4、7、9
3、△ABC中:
(1)若∠A=38°,∠B=62°,则∠C=______°;
(2)若∠A=40°,∠B=∠C,则∠C=______°;
(3) 若∠A=40°,∠B-∠C=20°,则∠C=______°;
(4) 若∠A+∠B=100°,∠C=2∠B,则∠C=______°;
(5)若∠A∶∠B∶∠C=1∶2∶3,∠A=_____°,∠B=______°;
(6)若∠A=∠B=∠C,则∠A=_____°,∠B=______°;
(7)若∠A=2∠B=3∠C,则∠A=_____°,∠B=______°;
(8)已知等腰三角形的一个内角为40°,则其他两个角的度数是_____°。
4、判断对错:
(1)三角形中最大的角是,那么这个三角形是锐角三角形( )
(2) 一个三角形中最多只有一个钝角或直角( )
(3) 一个等腰三角形一定是锐角三角形( )
(4) 一个三角形最少有一个角不大于( )
学习目标
1 经历实验活动的过程,得出三角形的内角和定理,能用平行线的性质推出这一定理
2 能应用三角形内角和定理解决一些简单的实际问题
重点:三角形内角和定理
难点:三角形内角和定理的推理的过程
课前准备
每个学生准备好二个由硬纸片剪出的三角形
学习过程
1、 做一做
1在所准备的三角形硬纸片上标出三个内角的编码
2 让学生动手把一个三角形的两个角剪下拼在第三个角的顶点处,用量角器量出的度数,可得到
3 剪下,按图(2)拼在一起,从而还可得到
图2
4 把和剪下按图(3)拼在一起,用量角器量一量的度数,会得到什么结果。
二、想一想、做一做、学生展示
如果我们不用剪、拼办法,可不可以用推理论证的方法来说明上面的结论的正确性呢?
已知,说明,你有几种方法?
结合图(3),自学课本73页,作出辅助线,写出你的推理过程。
结合图(1),作出辅助线,写出你的推理过程。
结合图(2),作出辅助线,写出你的推理过程。
能不能用图(4)也可以说明这个结论成立
三角形内角和定理:_____________________________________。
例题:如图,C岛在A岛的北偏东方向,B岛在A岛的北偏东方向,C岛在B岛的北偏西方向,从C岛看A、B两岛的视角是多少度?
你还能想出其它解法吗?
练习:
1、课本P74,练习1,2
2、课本76页习题7.2 1,2,3,4、7、9
3、△ABC中:
(1)若∠A=38°,∠B=62°,则∠C=______°;
(2)若∠A=40°,∠B=∠C,则∠C=______°;
(3) 若∠A=40°,∠B-∠C=20°,则∠C=______°;
(4) 若∠A+∠B=100°,∠C=2∠B,则∠C=______°;
(5)若∠A∶∠B∶∠C=1∶2∶3,∠A=_____°,∠B=______°;
(6)若∠A=∠B=∠C,则∠A=_____°,∠B=______°;
(7)若∠A=2∠B=3∠C,则∠A=_____°,∠B=______°;
(8)已知等腰三角形的一个内角为40°,则其他两个角的度数是_____°。
4、判断对错:
(1)三角形中最大的角是,那么这个三角形是锐角三角形( )
(2) 一个三角形中最多只有一个钝角或直角( )
(3) 一个等腰三角形一定是锐角三角形( )
(4) 一个三角形最少有一个角不大于( )
