2024-2025学年数学七年级下册人教版(2024)期末真题重组练习卷(含解析)
文档属性
| 名称 | 2024-2025学年数学七年级下册人教版(2024)期末真题重组练习卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 13:43:34 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024秋 涡阳县期末)4月23日为世界读书日,为了解七年级1400名学生的阅读时间,从中抽取70名学生进行调查,下列说法正确的是( )
A.每名学生是个体
B.样本容量是70名学生
C.70名学生是总体的一个样本
D.1400名学生的阅读时间是总体
2.(2023春 嘉鱼县期末)如图,数轴上表示不等式的解集为( )
A.x≥﹣1 B.x>﹣1 C.x≤﹣1 D.x<﹣1
3.(2024春 无为市期末)如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
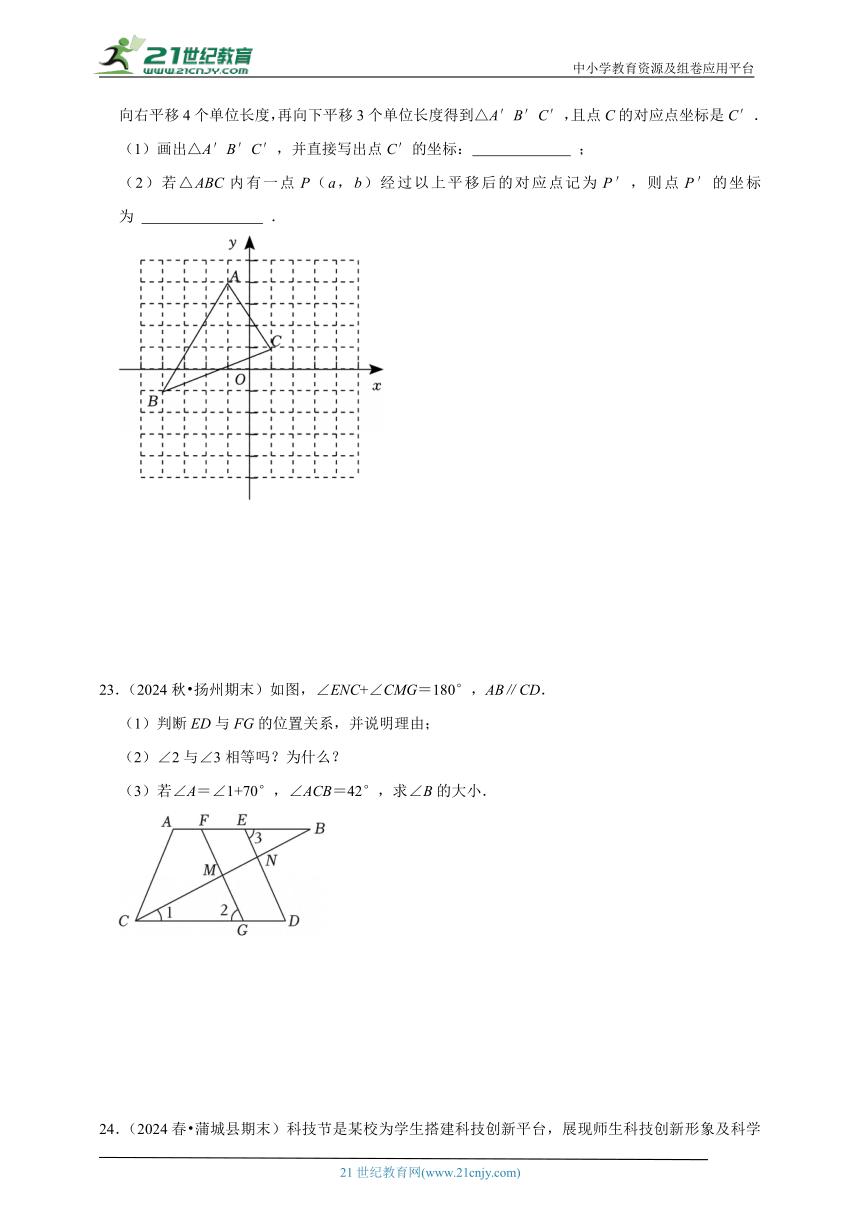
A.30° B.40° C.45° D.50°
4.(2024春 云梦县期末)64的平方根是( )
A.±4 B.4 C.±8 D.8
5.(2024春 沈阳期末)下列各图中,∠1=∠2的是( )
A. B.
C. D.
6.(2024秋 永春县期末)估计的值在( )
A.5和6之间 B.6和7之间 C.7和8之间 D.8和9之间
7.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
8.(2024秋 康平县期末)在某款游戏的周边制作中,某工厂安排工人制作手办和徽章.已知一共有60名工人参与制作,每人每天能制作手办5个或者徽章8个,且每1个手办要搭配3个徽章进行套装售卖,设安排x名工人制作手办,y名工人制作徽章,能恰好全部配成套装,下面所列方程组正确的是( )
A. B.
C. D.
二.填空题(共8小题)
9.(2025春 虹口区校级期末)x|m﹣2|+(m﹣3)y=m﹣1是关于x,y的二元一次方程,则实数m= .
10.(2025春 虹口区校级期末)关于x的不等式﹣k﹣x+6>0的解集中恰有四个非负整数,则k的范围为 .
11.(2020秋 宁德期末)一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有 个.
12.(2022春 仙居县期末)如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是 .
13.(2025春 河西区校级期末)如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= .
14.(2025春 河西区校级期末)已知AB∥y轴,A(1,﹣2),B在第一象限且AB=8,则B点的坐标为 .
15.(2024秋 简阳市期末)“昔锦官之地,有匠作弓与箭.作一弓需三日,作一箭需二日.共费四十日,成弓箭十五.”题目大意是:从前在锦官城这个地方,有工匠制作弓和箭.制作一张弓需要三天时间,制作一支箭需要两天时间.总共花费四十天时间,制成弓和箭共计十五件.设弓有x件,箭有y件,则可列方程组为 .
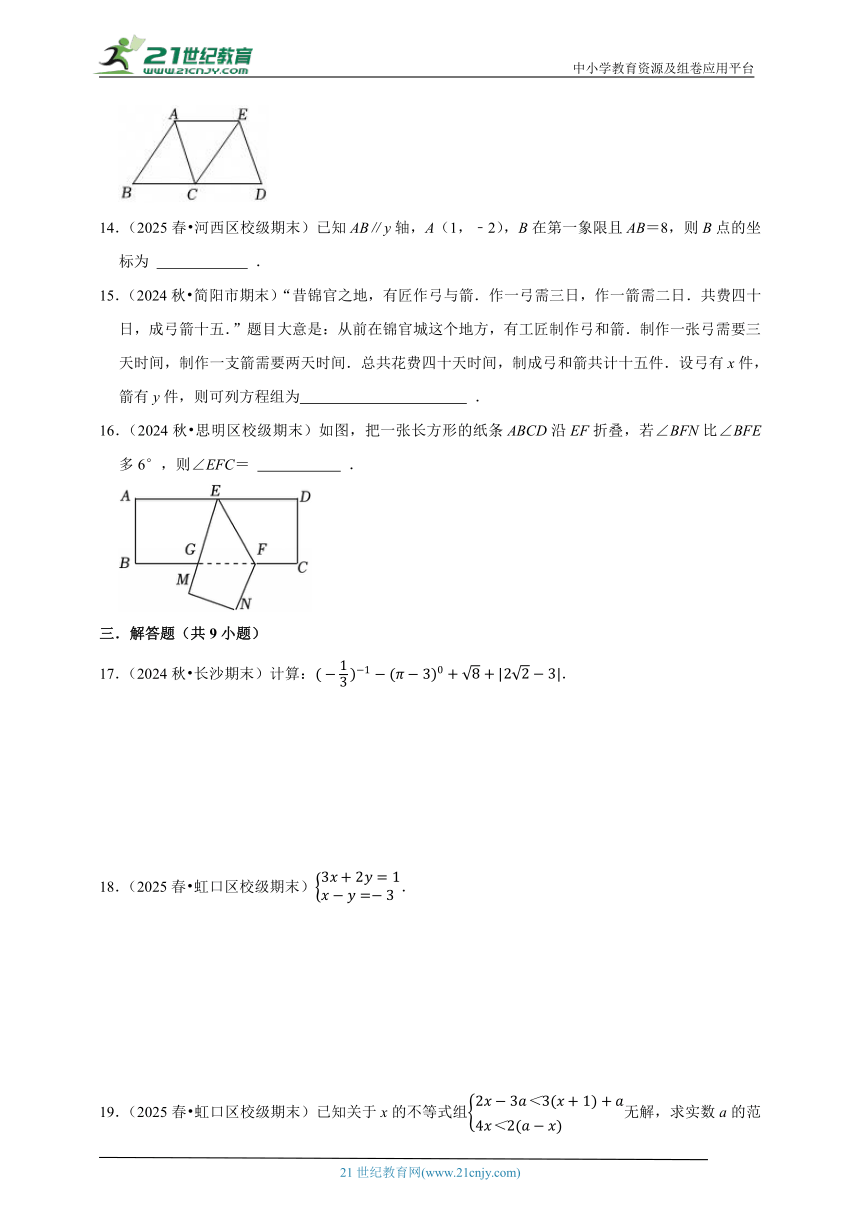
16.(2024秋 思明区校级期末)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= .
三.解答题(共9小题)
17.(2024秋 长沙期末)计算:.
18.(2025春 虹口区校级期末).
19.(2025春 虹口区校级期末)已知关于x的不等式组无解,求实数a的范围.
20.(2024秋 卫辉市期末)已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21.(2021秋 锦州期末)某初中开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢键子、篮球、跳绳、健美操四种运动项目(分别用A,B,C,D表示),为了解学生最喜欢哪一种运动项目,随机抽取了部分学生进行调查(每个被调查的学生必须选择一种且只能选择一种).并将调查结果绘制成如下两幅不完整的统计图.请结合图中的信息解答下列问题:
(1)本次共调查学生 名;
(2)请补全条形统计图,并求扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该校有1500名学生,喜欢篮球运动的学生约有多少名?
22.(2024秋 涡阳县期末)如图,△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).若△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A′B′C′,且点C的对应点坐标是C′.
(1)画出△A′B′C′,并直接写出点C′的坐标: ;
(2)若△ABC内有一点P(a,b)经过以上平移后的对应点记为P′,则点P′的坐标为 .
23.(2024秋 扬州期末)如图,∠ENC+∠CMG=180°,AB∥CD.
(1)判断ED与FG的位置关系,并说明理由;
(2)∠2与∠3相等吗?为什么?
(3)若∠A=∠1+70°,∠ACB=42°,求∠B的大小.
24.(2024春 蒲城县期末)科技节是某校为学生搭建科技创新平台,展现师生科技创新形象及科学素养的重大节日.该校在科技节活动中开展了以“科技创造未来”为主题的科普知识竞赛,各班选派一名同学参加,其中某一环节共有25道题,答对一题得4分,答错或不答每题扣2分,得分不低于88分将有奖品赠送.如果参赛选手想在本环节中获得奖品,则他至少需要答对多少道题?
25.(2024秋 东海县期末)【习题再现】
(1)苏科版初中数学教材七上第194第10题:如图1,AB∥CD,点E在AB,CD之间.写出∠AEC,∠A,∠C之间的数量关系,并说明理由;
【迁移思考】
(2)小明在完成第10题的探究后,对该页的第5题又作了探究与变式思考:
①如图2,在长方体盒底部有一面平面镜,点A处有一个光源,光线的入射角等于反射角,法线OE与平面镜l垂直,即OE⊥BC,垂足为O,入射光线经过镜面发射后,恰好经过点D.小明认为,图中∠AOB=∠COD,请帮小明说明理由;
②如图3,在长方体盒子里放置4块平面镜AB,BC,CD,DA,其中AD∥CB,若光线从AD上的E处射出,在平面镜AB上经点F反射后,到达BC上的点G,…其传播路径为E→F→G→H→E→F…请判断∠EFG与∠GHE的数量关系,并说明理由.
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B C A A B C
一.选择题(共8小题)
1.(2024秋 涡阳县期末)4月23日为世界读书日,为了解七年级1400名学生的阅读时间,从中抽取70名学生进行调查,下列说法正确的是( )
A.每名学生是个体
B.样本容量是70名学生
C.70名学生是总体的一个样本
D.1400名学生的阅读时间是总体
【解答】解:A、每个学生的阅读时间是个体,故A不符合题意;
B、样本容量是70,故B不符合题意;
C、70名学生的阅读时间是总体的一个样本,故C不符合题意;
D、1400名学生的阅读时间是总体,故D符合题意;
故选:D.
2.(2023春 嘉鱼县期末)如图,数轴上表示不等式的解集为( )
A.x≥﹣1 B.x>﹣1 C.x≤﹣1 D.x<﹣1
【解答】解:如图,数轴上表示不等式的解集为x≥﹣1,
故选:A.
3.(2024春 无为市期末)如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
A.30° B.40° C.45° D.50°
【解答】解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵直线AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:B.
4.(2024春 云梦县期末)64的平方根是( )
A.±4 B.4 C.±8 D.8
【解答】解:∵±8的平方都等于64;
∴64的平方根是±8.
故选:C.
5.(2024春 沈阳期末)下列各图中,∠1=∠2的是( )
A. B.
C. D.
【解答】解:A.∠1与∠2是对顶角,故A选项符合题意;
B.∠1与∠2互为邻补角,故B选项不符合题意;
C.∠1与∠2是同位角,但是不相等,故C选项不符合题意;
D.∠1与∠2是内错角,但是不相等,故D选项不符合题意.
故选:A.
6.(2024秋 永春县期末)估计的值在( )
A.5和6之间 B.6和7之间 C.7和8之间 D.8和9之间
【解答】解:∵25<29<36,
∴,
即56,
故选:A.
7.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
【解答】解:过A作AF∥BC,
∵BC∥DE,
∴AF∥DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB﹣∠FAD=30°.
故选:B.
8.(2024秋 康平县期末)在某款游戏的周边制作中,某工厂安排工人制作手办和徽章.已知一共有60名工人参与制作,每人每天能制作手办5个或者徽章8个,且每1个手办要搭配3个徽章进行套装售卖,设安排x名工人制作手办,y名工人制作徽章,能恰好全部配成套装,下面所列方程组正确的是( )
A. B.
C. D.
【解答】解:由题意得:,
故选:C.
二.填空题(共8小题)
9.(2025春 虹口区校级期末)x|m﹣2|+(m﹣3)y=m﹣1是关于x,y的二元一次方程,则实数m= 1 .
【解答】解:根据题意得|m﹣2|=1且m﹣3≠0,
解得m=1,
故答案为:1.
10.(2025春 虹口区校级期末)关于x的不等式﹣k﹣x+6>0的解集中恰有四个非负整数,则k的范围为 2≤k<3 .
【解答】解:由不等式﹣k﹣x+6>0得,
x<﹣k+6.
因为此不等式的解集中恰有四个非负整数,
所以3<﹣k+6≤4,
解得2≤k<3.
故答案为:2≤k<3.
11.(2020秋 宁德期末)一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有 15 个.
【解答】解:设盒子中白球大约有x个,
根据题意,得:0.25,
解得x=15,
经检验x=15是分式方程的解,
所以估计盒子中白球大约有15个,
故答案为:15.
12.(2022春 仙居县期末)如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是 垂线段最短 .
【解答】解:如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是垂线段最短,
故答案为:垂线段最短.
13.(2025春 河西区校级期末)如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= 12 .
【解答】解:∵△ABC沿直线BD方向向右平移,得到△ECD,
∴,
∵BD=24
∴AE=12,
故答案为:12.
14.(2025春 河西区校级期末)已知AB∥y轴,A(1,﹣2),B在第一象限且AB=8,则B点的坐标为 (1,6) .
【解答】解:∵AB∥y轴,A(1,﹣2),
∴点B的横坐标为1,
若点B在点A的上边,则点B的纵坐标为﹣2+8=6,
若点B在点A的下边,则点B的纵坐标为﹣2﹣8=﹣10,
所以,点B的坐标为:(1,﹣10)(舍去)或(1,6).
故答案为:(1,6).
15.(2024秋 简阳市期末)“昔锦官之地,有匠作弓与箭.作一弓需三日,作一箭需二日.共费四十日,成弓箭十五.”题目大意是:从前在锦官城这个地方,有工匠制作弓和箭.制作一张弓需要三天时间,制作一支箭需要两天时间.总共花费四十天时间,制成弓和箭共计十五件.设弓有x件,箭有y件,则可列方程组为 .
【解答】解:根据题意可列方程组.
故答案为:.
16.(2024秋 思明区校级期末)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= 122° .
【解答】解:根据折叠的性质得,∠EFC=∠EFN,
∵∠BFN比∠BFE多6°,
∴∠BFN=∠BFE+6°,
∴∠EFC=∠EFN=∠BFN+∠BFE=2∠BFE+6°,
∵∠BFE+∠EFC=180°,
∴2∠BFE+6°+∠BFE=180°,
∴∠BFE=58°,
∴∠EFC=180°﹣58°=122°,
故答案为:122°.
三.解答题(共9小题)
17.(2024秋 长沙期末)计算:.
【解答】解:
=﹣3﹣1
=﹣1.
18.(2025春 虹口区校级期末).
【解答】解:,
②×2,得2x﹣2y=﹣6③,
①+③,得5x=﹣5,
解得x=﹣1,
把x=﹣1代入②,得y=2,
所以方程组的解是.
19.(2025春 虹口区校级期末)已知关于x的不等式组无解,求实数a的范围.
【解答】解:,
解不等式①得:x>﹣4a﹣3,
解不等式②得:xa,
∵不等式组无解,
∴﹣4a﹣3a,
解得:a.
20.(2024秋 卫辉市期末)已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
【解答】解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2,
又∵34,
∴的整数部分c=3,
即a=5,b=2,c=3;
(2)当a=5,b=2,c=3时,3a﹣b+c=15﹣2+3=16,
∴3a﹣b+c的平方根为±4.
21.(2021秋 锦州期末)某初中开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢键子、篮球、跳绳、健美操四种运动项目(分别用A,B,C,D表示),为了解学生最喜欢哪一种运动项目,随机抽取了部分学生进行调查(每个被调查的学生必须选择一种且只能选择一种).并将调查结果绘制成如下两幅不完整的统计图.请结合图中的信息解答下列问题:
(1)本次共调查学生 200 名;
(2)请补全条形统计图,并求扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该校有1500名学生,喜欢篮球运动的学生约有多少名?
【解答】解:(1)本次共调查学生30÷15%=200(名),
故答案为:200;
(2)B项目对应的人数为200×30%=60(名),
补全图形如下:
扇形统计图中C部分所对应的扇形圆心角的度数为360°126°;
(3)喜欢篮球运动的学生约有1500×30%=450(名).
22.(2024秋 涡阳县期末)如图,△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).若△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A′B′C′,且点C的对应点坐标是C′.
(1)画出△A′B′C′,并直接写出点C′的坐标: (5,﹣2) ;
(2)若△ABC内有一点P(a,b)经过以上平移后的对应点记为P′,则点P′的坐标为 (a+4,b﹣3) .
【解答】解:(1)如图,△A′B′C′即为所作,
由图可知C′(5,﹣2).
故答案为:C′(5,﹣2);
(2)∵P(a,b)经过以上平移后的对应点记为P′,且平移方式为向右平移4个单位长度,再向下平移3个单位长度,
∴P′(a+4,b﹣3).
故答案为:(a+4,b﹣3).
23.(2024秋 扬州期末)如图,∠ENC+∠CMG=180°,AB∥CD.
(1)判断ED与FG的位置关系,并说明理由;
(2)∠2与∠3相等吗?为什么?
(3)若∠A=∠1+70°,∠ACB=42°,求∠B的大小.
【解答】解:(1)ED∥FG,理由如下:
∵∠ENC+∠CMG=180°,∠CMG=∠FMN,
∴∠ENC+∠FMN=180°,
∴ED∥FG;
(2)∠2=∠3,理由如下:
∵ED∥FG,
∴∠2=∠D,
∵AB∥CD,
∴∠3=∠D,
∴∠2=∠3;
(3)∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=∠1+70°,∠ACB=42°,
∴(∠1+70°)+(∠1+42°)=180°,
∴∠1=34°,
∵AB∥CD,
∴∠B=∠1=34°.
24.(2024春 蒲城县期末)科技节是某校为学生搭建科技创新平台,展现师生科技创新形象及科学素养的重大节日.该校在科技节活动中开展了以“科技创造未来”为主题的科普知识竞赛,各班选派一名同学参加,其中某一环节共有25道题,答对一题得4分,答错或不答每题扣2分,得分不低于88分将有奖品赠送.如果参赛选手想在本环节中获得奖品,则他至少需要答对多少道题?
【解答】解:设他答对x道题,则答错或不答的题为(25﹣x)道,
根据题意得,4x﹣2(25﹣x)≥88,
解得x≥23,
答:他至少需要答对23道题.
25.(2024秋 东海县期末)【习题再现】
(1)苏科版初中数学教材七上第194第10题:如图1,AB∥CD,点E在AB,CD之间.写出∠AEC,∠A,∠C之间的数量关系,并说明理由;
【迁移思考】
(2)小明在完成第10题的探究后,对该页的第5题又作了探究与变式思考:
①如图2,在长方体盒底部有一面平面镜,点A处有一个光源,光线的入射角等于反射角,法线OE与平面镜l垂直,即OE⊥BC,垂足为O,入射光线经过镜面发射后,恰好经过点D.小明认为,图中∠AOB=∠COD,请帮小明说明理由;
②如图3,在长方体盒子里放置4块平面镜AB,BC,CD,DA,其中AD∥CB,若光线从AD上的E处射出,在平面镜AB上经点F反射后,到达BC上的点G,…其传播路径为E→F→G→H→E→F…请判断∠EFG与∠GHE的数量关系,并说明理由.
【解答】解:(1)∠AEC,∠A,∠C之间的数量关系是:∠AEC=∠A+∠C,理由如下:
过点E作EM∥AB,如图所示:
∵AB∥CD,
∴AB∥EM∥CD,
∴∠AEM=∠A,∠CEM=∠C,
∴∠AEM+∠CEM=∠A+∠C,
∵∠AEC=∠AEM+∠CEM,
∴∠AEC=∠A+∠C,
(2)①理由如下:
∵OE⊥BC,
∴∠EOC=∠EOD=90°,
∴∠AOE+∠AOB=∠DOE+∠COD=90°,
∵光线的入射角等于反射角,
∴∠AOE=∠DOE,
∴∠AOB=∠COD;
②∠EFG与∠GHE的数量关系是:∠EFG=∠GHE,理由如下:
由(2)的结论得:∠AEF=∠DEH,∠BGF=∠CGH,
∴∠AEF+∠BGF=∠DEH+∠CGH,
∵AD∥CB,
由(1)的结论得:∠EFG=∠AEF+∠BGF,∠EHG=∠DEH+∠CGH,
∴∠EFG=∠EHG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024秋 涡阳县期末)4月23日为世界读书日,为了解七年级1400名学生的阅读时间,从中抽取70名学生进行调查,下列说法正确的是( )
A.每名学生是个体
B.样本容量是70名学生
C.70名学生是总体的一个样本
D.1400名学生的阅读时间是总体
2.(2023春 嘉鱼县期末)如图,数轴上表示不等式的解集为( )
A.x≥﹣1 B.x>﹣1 C.x≤﹣1 D.x<﹣1
3.(2024春 无为市期末)如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
A.30° B.40° C.45° D.50°
4.(2024春 云梦县期末)64的平方根是( )
A.±4 B.4 C.±8 D.8
5.(2024春 沈阳期末)下列各图中,∠1=∠2的是( )
A. B.
C. D.
6.(2024秋 永春县期末)估计的值在( )
A.5和6之间 B.6和7之间 C.7和8之间 D.8和9之间
7.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
8.(2024秋 康平县期末)在某款游戏的周边制作中,某工厂安排工人制作手办和徽章.已知一共有60名工人参与制作,每人每天能制作手办5个或者徽章8个,且每1个手办要搭配3个徽章进行套装售卖,设安排x名工人制作手办,y名工人制作徽章,能恰好全部配成套装,下面所列方程组正确的是( )
A. B.
C. D.
二.填空题(共8小题)
9.(2025春 虹口区校级期末)x|m﹣2|+(m﹣3)y=m﹣1是关于x,y的二元一次方程,则实数m= .
10.(2025春 虹口区校级期末)关于x的不等式﹣k﹣x+6>0的解集中恰有四个非负整数,则k的范围为 .
11.(2020秋 宁德期末)一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有 个.
12.(2022春 仙居县期末)如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是 .
13.(2025春 河西区校级期末)如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= .
14.(2025春 河西区校级期末)已知AB∥y轴,A(1,﹣2),B在第一象限且AB=8,则B点的坐标为 .
15.(2024秋 简阳市期末)“昔锦官之地,有匠作弓与箭.作一弓需三日,作一箭需二日.共费四十日,成弓箭十五.”题目大意是:从前在锦官城这个地方,有工匠制作弓和箭.制作一张弓需要三天时间,制作一支箭需要两天时间.总共花费四十天时间,制成弓和箭共计十五件.设弓有x件,箭有y件,则可列方程组为 .
16.(2024秋 思明区校级期末)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= .
三.解答题(共9小题)
17.(2024秋 长沙期末)计算:.
18.(2025春 虹口区校级期末).
19.(2025春 虹口区校级期末)已知关于x的不等式组无解,求实数a的范围.
20.(2024秋 卫辉市期末)已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
21.(2021秋 锦州期末)某初中开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢键子、篮球、跳绳、健美操四种运动项目(分别用A,B,C,D表示),为了解学生最喜欢哪一种运动项目,随机抽取了部分学生进行调查(每个被调查的学生必须选择一种且只能选择一种).并将调查结果绘制成如下两幅不完整的统计图.请结合图中的信息解答下列问题:
(1)本次共调查学生 名;
(2)请补全条形统计图,并求扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该校有1500名学生,喜欢篮球运动的学生约有多少名?
22.(2024秋 涡阳县期末)如图,△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).若△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A′B′C′,且点C的对应点坐标是C′.
(1)画出△A′B′C′,并直接写出点C′的坐标: ;
(2)若△ABC内有一点P(a,b)经过以上平移后的对应点记为P′,则点P′的坐标为 .
23.(2024秋 扬州期末)如图,∠ENC+∠CMG=180°,AB∥CD.
(1)判断ED与FG的位置关系,并说明理由;
(2)∠2与∠3相等吗?为什么?
(3)若∠A=∠1+70°,∠ACB=42°,求∠B的大小.
24.(2024春 蒲城县期末)科技节是某校为学生搭建科技创新平台,展现师生科技创新形象及科学素养的重大节日.该校在科技节活动中开展了以“科技创造未来”为主题的科普知识竞赛,各班选派一名同学参加,其中某一环节共有25道题,答对一题得4分,答错或不答每题扣2分,得分不低于88分将有奖品赠送.如果参赛选手想在本环节中获得奖品,则他至少需要答对多少道题?
25.(2024秋 东海县期末)【习题再现】
(1)苏科版初中数学教材七上第194第10题:如图1,AB∥CD,点E在AB,CD之间.写出∠AEC,∠A,∠C之间的数量关系,并说明理由;
【迁移思考】
(2)小明在完成第10题的探究后,对该页的第5题又作了探究与变式思考:
①如图2,在长方体盒底部有一面平面镜,点A处有一个光源,光线的入射角等于反射角,法线OE与平面镜l垂直,即OE⊥BC,垂足为O,入射光线经过镜面发射后,恰好经过点D.小明认为,图中∠AOB=∠COD,请帮小明说明理由;
②如图3,在长方体盒子里放置4块平面镜AB,BC,CD,DA,其中AD∥CB,若光线从AD上的E处射出,在平面镜AB上经点F反射后,到达BC上的点G,…其传播路径为E→F→G→H→E→F…请判断∠EFG与∠GHE的数量关系,并说明理由.
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D A B C A A B C
一.选择题(共8小题)
1.(2024秋 涡阳县期末)4月23日为世界读书日,为了解七年级1400名学生的阅读时间,从中抽取70名学生进行调查,下列说法正确的是( )
A.每名学生是个体
B.样本容量是70名学生
C.70名学生是总体的一个样本
D.1400名学生的阅读时间是总体
【解答】解:A、每个学生的阅读时间是个体,故A不符合题意;
B、样本容量是70,故B不符合题意;
C、70名学生的阅读时间是总体的一个样本,故C不符合题意;
D、1400名学生的阅读时间是总体,故D符合题意;
故选:D.
2.(2023春 嘉鱼县期末)如图,数轴上表示不等式的解集为( )
A.x≥﹣1 B.x>﹣1 C.x≤﹣1 D.x<﹣1
【解答】解:如图,数轴上表示不等式的解集为x≥﹣1,
故选:A.
3.(2024春 无为市期末)如图,直线a∥b,直线AB⊥AC,若∠1=50°,则∠2=( )
A.30° B.40° C.45° D.50°
【解答】解:∵直线a∥b,∠1=50°,
∴∠1=∠3=50°,
∵直线AB⊥AC,
∴∠2+∠3=90°.
∴∠2=40°.
故选:B.
4.(2024春 云梦县期末)64的平方根是( )
A.±4 B.4 C.±8 D.8
【解答】解:∵±8的平方都等于64;
∴64的平方根是±8.
故选:C.
5.(2024春 沈阳期末)下列各图中,∠1=∠2的是( )
A. B.
C. D.
【解答】解:A.∠1与∠2是对顶角,故A选项符合题意;
B.∠1与∠2互为邻补角,故B选项不符合题意;
C.∠1与∠2是同位角,但是不相等,故C选项不符合题意;
D.∠1与∠2是内错角,但是不相等,故D选项不符合题意.
故选:A.
6.(2024秋 永春县期末)估计的值在( )
A.5和6之间 B.6和7之间 C.7和8之间 D.8和9之间
【解答】解:∵25<29<36,
∴,
即56,
故选:A.
7.(2024秋 中牟县期末)为增强学生体质,感受中国传统文化,某初中将国家级非物质文化遗产“抖空竹”引入阳光特色大课间.如图①是某同学“抖空竹”时的一个瞬间,小玲把它抽象成图②的数学问题:已知BC∥DE,∠ADE=80°,∠ABC=110°,则∠A的度数是( )
A.40° B.30° C.20° D.10°
【解答】解:过A作AF∥BC,
∵BC∥DE,
∴AF∥DE,
∴∠FAD=∠ADE=80°,∠FAB=∠ABC=110°,
∴∠BAD=∠FAB﹣∠FAD=30°.
故选:B.
8.(2024秋 康平县期末)在某款游戏的周边制作中,某工厂安排工人制作手办和徽章.已知一共有60名工人参与制作,每人每天能制作手办5个或者徽章8个,且每1个手办要搭配3个徽章进行套装售卖,设安排x名工人制作手办,y名工人制作徽章,能恰好全部配成套装,下面所列方程组正确的是( )
A. B.
C. D.
【解答】解:由题意得:,
故选:C.
二.填空题(共8小题)
9.(2025春 虹口区校级期末)x|m﹣2|+(m﹣3)y=m﹣1是关于x,y的二元一次方程,则实数m= 1 .
【解答】解:根据题意得|m﹣2|=1且m﹣3≠0,
解得m=1,
故答案为:1.
10.(2025春 虹口区校级期末)关于x的不等式﹣k﹣x+6>0的解集中恰有四个非负整数,则k的范围为 2≤k<3 .
【解答】解:由不等式﹣k﹣x+6>0得,
x<﹣k+6.
因为此不等式的解集中恰有四个非负整数,
所以3<﹣k+6≤4,
解得2≤k<3.
故答案为:2≤k<3.
11.(2020秋 宁德期末)一个盒子中有5个红球和若干个白球,它们除颜色外都相同,从中随机摸出一个球,记下它的颜色后再放回盒子中.不断重复这个过程,共摸了100次球,发现有25次摸到红球,请估计盒子中白球大约有 15 个.
【解答】解:设盒子中白球大约有x个,
根据题意,得:0.25,
解得x=15,
经检验x=15是分式方程的解,
所以估计盒子中白球大约有15个,
故答案为:15.
12.(2022春 仙居县期末)如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是 垂线段最短 .
【解答】解:如图,小华同学的家在点P处,他想尽快到公路边,所以选择沿线段PC去公路边,那么他的这一选择体现的数学基本事实是垂线段最短,
故答案为:垂线段最短.
13.(2025春 河西区校级期末)如图,将△ABC沿直线BD方向向右平移,得到△ECD,若BD=24,则AE= 12 .
【解答】解:∵△ABC沿直线BD方向向右平移,得到△ECD,
∴,
∵BD=24
∴AE=12,
故答案为:12.
14.(2025春 河西区校级期末)已知AB∥y轴,A(1,﹣2),B在第一象限且AB=8,则B点的坐标为 (1,6) .
【解答】解:∵AB∥y轴,A(1,﹣2),
∴点B的横坐标为1,
若点B在点A的上边,则点B的纵坐标为﹣2+8=6,
若点B在点A的下边,则点B的纵坐标为﹣2﹣8=﹣10,
所以,点B的坐标为:(1,﹣10)(舍去)或(1,6).
故答案为:(1,6).
15.(2024秋 简阳市期末)“昔锦官之地,有匠作弓与箭.作一弓需三日,作一箭需二日.共费四十日,成弓箭十五.”题目大意是:从前在锦官城这个地方,有工匠制作弓和箭.制作一张弓需要三天时间,制作一支箭需要两天时间.总共花费四十天时间,制成弓和箭共计十五件.设弓有x件,箭有y件,则可列方程组为 .
【解答】解:根据题意可列方程组.
故答案为:.
16.(2024秋 思明区校级期末)如图,把一张长方形的纸条ABCD沿EF折叠,若∠BFN比∠BFE多6°,则∠EFC= 122° .
【解答】解:根据折叠的性质得,∠EFC=∠EFN,
∵∠BFN比∠BFE多6°,
∴∠BFN=∠BFE+6°,
∴∠EFC=∠EFN=∠BFN+∠BFE=2∠BFE+6°,
∵∠BFE+∠EFC=180°,
∴2∠BFE+6°+∠BFE=180°,
∴∠BFE=58°,
∴∠EFC=180°﹣58°=122°,
故答案为:122°.
三.解答题(共9小题)
17.(2024秋 长沙期末)计算:.
【解答】解:
=﹣3﹣1
=﹣1.
18.(2025春 虹口区校级期末).
【解答】解:,
②×2,得2x﹣2y=﹣6③,
①+③,得5x=﹣5,
解得x=﹣1,
把x=﹣1代入②,得y=2,
所以方程组的解是.
19.(2025春 虹口区校级期末)已知关于x的不等式组无解,求实数a的范围.
【解答】解:,
解不等式①得:x>﹣4a﹣3,
解不等式②得:xa,
∵不等式组无解,
∴﹣4a﹣3a,
解得:a.
20.(2024秋 卫辉市期末)已知5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
(1)求a,b,c的值;
(2)求3a﹣b+c的平方根.
【解答】解:(1)∵5a+2的立方根是3,3a+b﹣1的算术平方根是4,c是的整数部分;
∴5a+2=27,3a+b﹣1=16,
∴a=5,b=2,
又∵34,
∴的整数部分c=3,
即a=5,b=2,c=3;
(2)当a=5,b=2,c=3时,3a﹣b+c=15﹣2+3=16,
∴3a﹣b+c的平方根为±4.
21.(2021秋 锦州期末)某初中开展“阳光体育一小时”活动,根据学校实际情况,决定开设踢键子、篮球、跳绳、健美操四种运动项目(分别用A,B,C,D表示),为了解学生最喜欢哪一种运动项目,随机抽取了部分学生进行调查(每个被调查的学生必须选择一种且只能选择一种).并将调查结果绘制成如下两幅不完整的统计图.请结合图中的信息解答下列问题:
(1)本次共调查学生 200 名;
(2)请补全条形统计图,并求扇形统计图中C部分所对应的扇形圆心角的度数;
(3)若该校有1500名学生,喜欢篮球运动的学生约有多少名?
【解答】解:(1)本次共调查学生30÷15%=200(名),
故答案为:200;
(2)B项目对应的人数为200×30%=60(名),
补全图形如下:
扇形统计图中C部分所对应的扇形圆心角的度数为360°126°;
(3)喜欢篮球运动的学生约有1500×30%=450(名).
22.(2024秋 涡阳县期末)如图,△ABC的顶点A(﹣1,4),B(﹣4,﹣1),C(1,1).若△ABC向右平移4个单位长度,再向下平移3个单位长度得到△A′B′C′,且点C的对应点坐标是C′.
(1)画出△A′B′C′,并直接写出点C′的坐标: (5,﹣2) ;
(2)若△ABC内有一点P(a,b)经过以上平移后的对应点记为P′,则点P′的坐标为 (a+4,b﹣3) .
【解答】解:(1)如图,△A′B′C′即为所作,
由图可知C′(5,﹣2).
故答案为:C′(5,﹣2);
(2)∵P(a,b)经过以上平移后的对应点记为P′,且平移方式为向右平移4个单位长度,再向下平移3个单位长度,
∴P′(a+4,b﹣3).
故答案为:(a+4,b﹣3).
23.(2024秋 扬州期末)如图,∠ENC+∠CMG=180°,AB∥CD.
(1)判断ED与FG的位置关系,并说明理由;
(2)∠2与∠3相等吗?为什么?
(3)若∠A=∠1+70°,∠ACB=42°,求∠B的大小.
【解答】解:(1)ED∥FG,理由如下:
∵∠ENC+∠CMG=180°,∠CMG=∠FMN,
∴∠ENC+∠FMN=180°,
∴ED∥FG;
(2)∠2=∠3,理由如下:
∵ED∥FG,
∴∠2=∠D,
∵AB∥CD,
∴∠3=∠D,
∴∠2=∠3;
(3)∵AB∥CD,
∴∠A+∠ACD=180°,
∵∠A=∠1+70°,∠ACB=42°,
∴(∠1+70°)+(∠1+42°)=180°,
∴∠1=34°,
∵AB∥CD,
∴∠B=∠1=34°.
24.(2024春 蒲城县期末)科技节是某校为学生搭建科技创新平台,展现师生科技创新形象及科学素养的重大节日.该校在科技节活动中开展了以“科技创造未来”为主题的科普知识竞赛,各班选派一名同学参加,其中某一环节共有25道题,答对一题得4分,答错或不答每题扣2分,得分不低于88分将有奖品赠送.如果参赛选手想在本环节中获得奖品,则他至少需要答对多少道题?
【解答】解:设他答对x道题,则答错或不答的题为(25﹣x)道,
根据题意得,4x﹣2(25﹣x)≥88,
解得x≥23,
答:他至少需要答对23道题.
25.(2024秋 东海县期末)【习题再现】
(1)苏科版初中数学教材七上第194第10题:如图1,AB∥CD,点E在AB,CD之间.写出∠AEC,∠A,∠C之间的数量关系,并说明理由;
【迁移思考】
(2)小明在完成第10题的探究后,对该页的第5题又作了探究与变式思考:
①如图2,在长方体盒底部有一面平面镜,点A处有一个光源,光线的入射角等于反射角,法线OE与平面镜l垂直,即OE⊥BC,垂足为O,入射光线经过镜面发射后,恰好经过点D.小明认为,图中∠AOB=∠COD,请帮小明说明理由;
②如图3,在长方体盒子里放置4块平面镜AB,BC,CD,DA,其中AD∥CB,若光线从AD上的E处射出,在平面镜AB上经点F反射后,到达BC上的点G,…其传播路径为E→F→G→H→E→F…请判断∠EFG与∠GHE的数量关系,并说明理由.
【解答】解:(1)∠AEC,∠A,∠C之间的数量关系是:∠AEC=∠A+∠C,理由如下:
过点E作EM∥AB,如图所示:
∵AB∥CD,
∴AB∥EM∥CD,
∴∠AEM=∠A,∠CEM=∠C,
∴∠AEM+∠CEM=∠A+∠C,
∵∠AEC=∠AEM+∠CEM,
∴∠AEC=∠A+∠C,
(2)①理由如下:
∵OE⊥BC,
∴∠EOC=∠EOD=90°,
∴∠AOE+∠AOB=∠DOE+∠COD=90°,
∵光线的入射角等于反射角,
∴∠AOE=∠DOE,
∴∠AOB=∠COD;
②∠EFG与∠GHE的数量关系是:∠EFG=∠GHE,理由如下:
由(2)的结论得:∠AEF=∠DEH,∠BGF=∠CGH,
∴∠AEF+∠BGF=∠DEH+∠CGH,
∵AD∥CB,
由(1)的结论得:∠EFG=∠AEF+∠BGF,∠EHG=∠DEH+∠CGH,
∴∠EFG=∠EHG.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
