人教版六年级下册数学期末专项训练:作图题(含解析)
文档属性
| 名称 | 人教版六年级下册数学期末专项训练:作图题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 14:57:11 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
人教版六年级下册数学期末专项训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
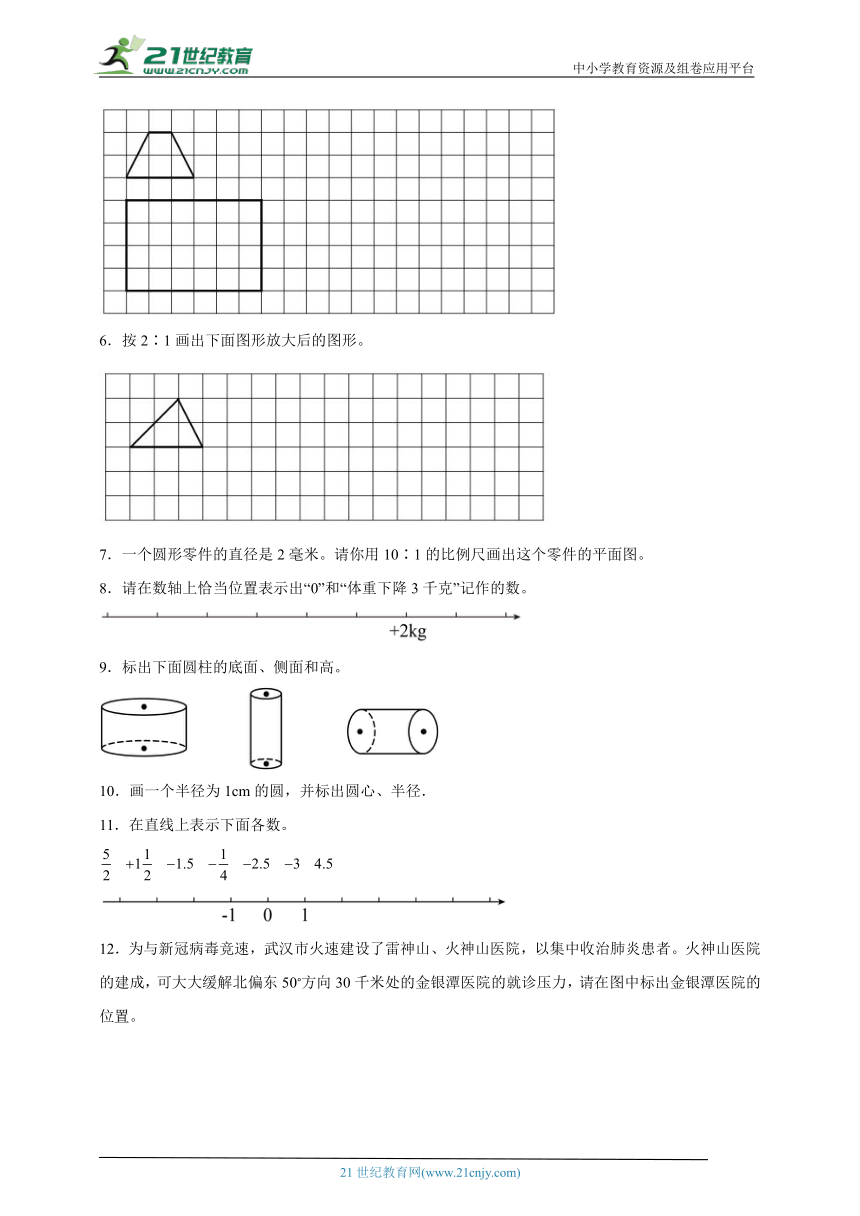
1.把下面图1的图形每边放大到原来的2倍,把图2的图形每边缩小到原来的.
2.先按4∶1把下面的三角形放大,再把放大后的图形按1∶2缩小。
3.按1∶4画出三角形缩小后的图形。
4.用圆规和三角尺画出下面的图案。你还能设计什么图案?
5.按2∶1画出梯形放大后的图形,按1∶2画出长方形缩小后的图形。
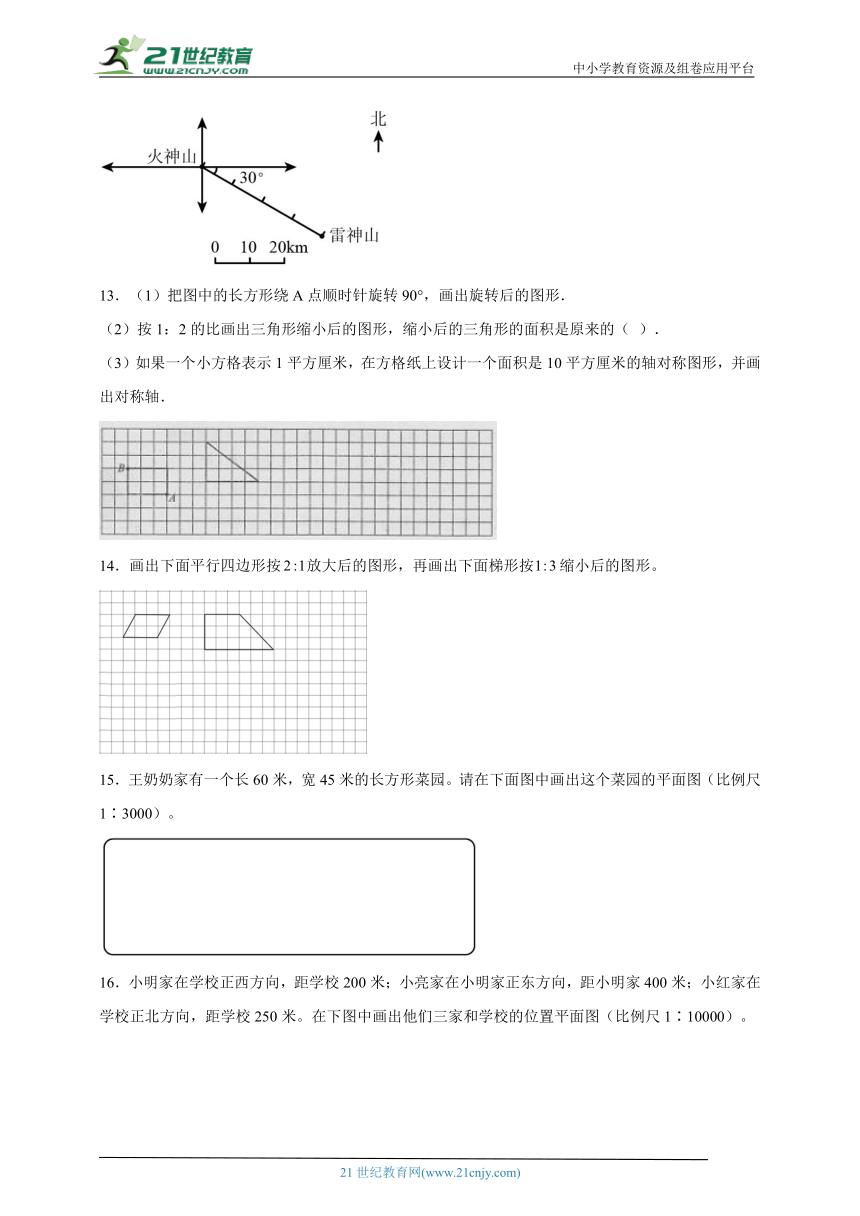
6.按2∶1画出下面图形放大后的图形。
7.一个圆形零件的直径是2毫米。请你用10∶1的比例尺画出这个零件的平面图。
8.请在数轴上恰当位置表示出“0”和“体重下降3千克”记作的数。
9.标出下面圆柱的底面、侧面和高。
10.画一个半径为1cm的圆,并标出圆心、半径.
11.在直线上表示下面各数。
12.为与新冠病毒竞速,武汉市火速建设了雷神山、火神山医院,以集中收治肺炎患者。火神山医院的建成,可大大缓解北偏东50 方向30千米处的金银潭医院的就诊压力,请在图中标出金银潭医院的位置。
13.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( ).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴.
14.画出下面平行四边形按放大后的图形,再画出下面梯形按缩小后的图形。
15.王奶奶家有一个长60米,宽45米的长方形菜园。请在下面图中画出这个菜园的平面图(比例尺1∶3000)。
16.小明家在学校正西方向,距学校200米;小亮家在小明家正东方向,距小明家400米;小红家在学校正北方向,距学校250米。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
想:先求出每家到学校的图上距离。根据“”,得到“图上距离=实际距离×比例尺”。
200米=20000厘米,400米=40000厘米,250米=25000厘米
小明家到学校的图上距离:(厘米)
小亮家到学校的图上距离:(厘米)
小红家到学校的图上距离:(厘米)
17.直线上每格代表100m,小乌龟的家在﹢1处。
①小乌龟从家出发,先走了﹢200m,之后又走了﹣500m到达了大象家。请用“△”标出大象家的位置。
②小乌龟又从大象家出发,先走了﹣200m,之后又走了﹢900m到达小狗家。请用“○”标出小狗家的位置。
18.按要求画图。
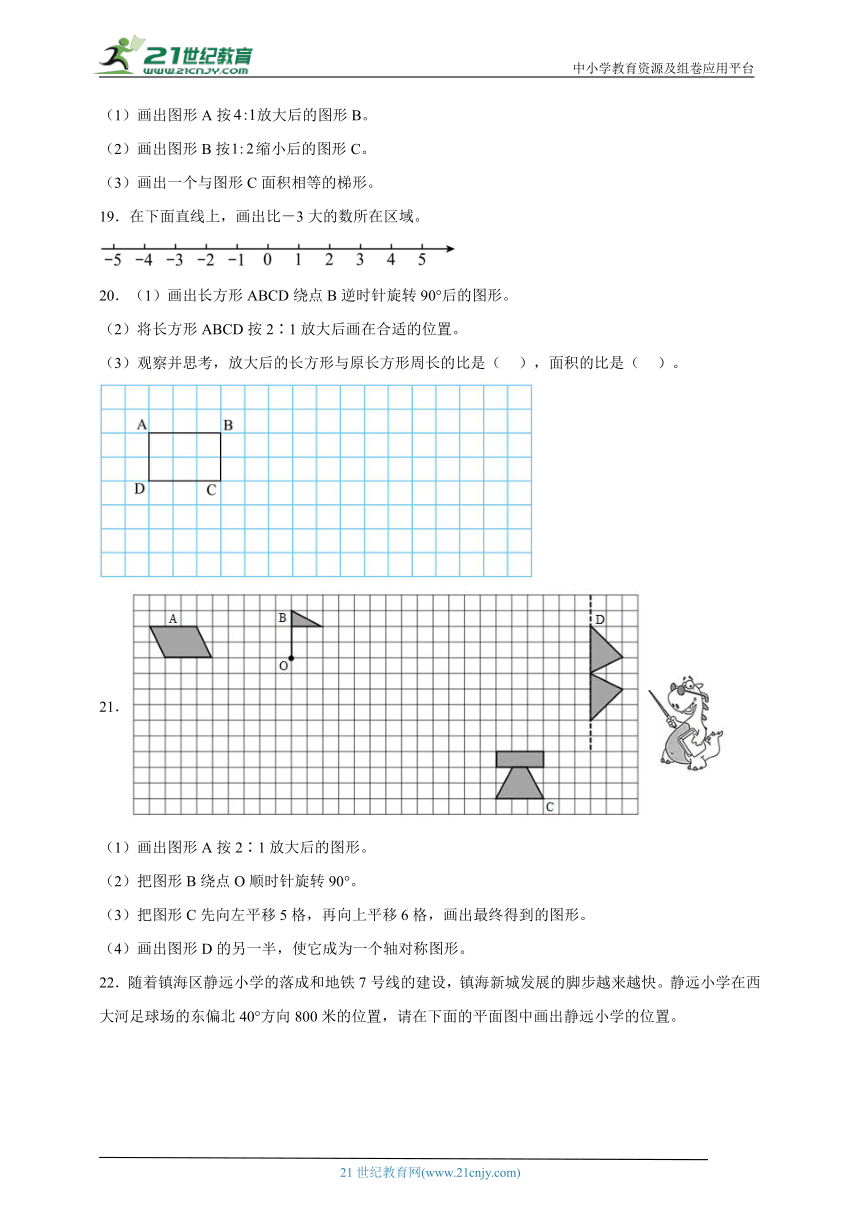
(1)画出图形A按放大后的图形B。
(2)画出图形B按缩小后的图形C。
(3)画出一个与图形C面积相等的梯形。
19.在下面直线上,画出比-3大的数所在区域。
20.(1)画出长方形ABCD绕点B逆时针旋转90°后的图形。
(2)将长方形ABCD按2∶1放大后画在合适的位置。
(3)观察并思考,放大后的长方形与原长方形周长的比是( ),面积的比是( )。
21.
(1)画出图形A按2∶1放大后的图形。
(2)把图形B绕点O顺时针旋转90°。
(3)把图形C先向左平移5格,再向上平移6格,画出最终得到的图形。
(4)画出图形D的另一半,使它成为一个轴对称图形。
22.随着镇海区静远小学的落成和地铁7号线的建设,镇海新城发展的脚步越来越快。静远小学在西大河足球场的东偏北40°方向800米的位置,请在下面的平面图中画出静远小学的位置。
23.操作。
(1)以O点为中心,按3∶1的比画出放大后的图形。
(2)放大前与放大后两个圆的面积比是( )。
(3)放大前与放大后两个圆的周长比是( )。
24.小红用若干个相同的小正方体摆了一个立体图形(如下图),在下面方格纸上分别画出从它的正面、上面和左面看到的形状。
25.按要求完成下面各题。
(1)画出图A的另一半,使它成为一个轴对称图形。
(2)把图B向右平移5格,再向上平移3格。
(3)把图C绕点O逆时针旋转90°。
(4)把图D按3∶1放大。
26.按的比画出下面图形放大后的图形。
27.指出下面圆锥的底面、侧面和高。
28.写出点A、B、C表示的数。
29.画出下面各个图形指定底边上的高.
30.将方格里的梯形面积按1:2:3分成三个三角形.
31.按3:1画出下面三个图形放大后的图形.
32.某市新建一个长方形运动场,长240m,宽120m,请在下面图中画出运动场的平面图.(比例尺:1:4000)
33.按要求完成。
(1)在如图中描出下面各点,并依此连成一个三角形;A(2,7)、B(6,7)、C(4,9)
(2)画出三角形向下平移5格后的图形;
(3)将三角形缩小为原来的,画在右边,要求点A画在A′上;
(4)画出正方形绕O点顺时针旋转180°后的图形,这时两个正方形组成了一个新图形,画出新图形的其中一条对称轴。
34.根据要求在下图中操作,并回答问题。
一只蚂蚁从点A沿东北方向爬到点B,又沿正南方向到点C,最后沿正西方向返回到A点。
(1)用数对表示A( )、B( )、C( )的位置。
(2)将三角形ABC沿点C顺时针方向旋转180度,画出旋转后的图形。
(3)画出旋转后按2∶1扩大的图形。
35.画一个圆锥,标出它的底面半径和高.
36.在下图中标出他们两家的位置。
37.指出下面圆柱的底面、侧面和高。
38.实验小学大门在教学楼的正南方向50米处,图书馆在教学楼的北偏东60°方向100米处.在下图中表示出大门和图书馆的位置.
39.(1)琪琪家在学校西偏北40°方向,距离学校1千米,请在下图中用“●”表示出琪琪家的位置。
(2)在下图中画出琪琪家到畅家巷的最短线段。
40.下面是仪征城区的平面图,请在图中画出有关街道和场所的位置。
(1)市政府东面300米的处有一条健康路,它与工农路平行。
(2)育才小学在市政府北偏西75°方向400米处。
41.下面三角形图中8个字.请你用笔画上6条线,将八卦巧分8块,每块形状是大小相等的三角形。
《人教版六年级下册数学期末专项训练:作图题》参考答案
1.
【详解】解:
分析:(1)把图①中各条边的长度扩大2倍,据此画出;
(2)把图②中各条边的长度缩小2倍,据此画出.
2.
【分析】按4∶1放大,就是把新图形的每条边长扩大到原来的4倍;按1∶2缩小,就是把新图形的每条边长缩小为原来的。
【详解】这是一个直角三角形,底2高1,按4∶1扩大后,底8高4;再按1∶2缩小,就是底4高2。
【点睛】通常把比例尺写成前项(或后项)为1的比,图上距离为前项,实际距离为后项,掌握好这些,作图就不难了。
3.见详解
【分析】把三角形按1∶4缩小,即三角形的每一条边缩小到原来的,原三角形的底和高分别除以4,得出缩小后三角形的底和高,据此画出缩小后的图形。
【详解】如图:
【点睛】本题考查图形的放大或缩小,明确放大或缩小的是图形的各个边长,图形的形状不变是解题的关键。
4.见详解
【分析】画图(1)只需要圆规:首先确定大圆圆心的位置,再以2厘米(不唯一)作为半径画出大圆,然后在大圆中画出两条互相垂直的直径(共4条半径),在每条半径的中点以1厘米(大圆半径的一半)为半径分别画出4个小圆。
画图(2)需要用到圆规和三角尺:同样先确定大圆的圆心,以2厘米(不唯一)为半径画出大圆,在大圆中画出三条直径,直径两两之间的夹角为60度,此时直径与圆形成6个交点,将其中三个相间隔的交点两两连接。
图案设计可自由发挥,合理即可。
【详解】画上图:
设计图案(答案不唯一):
5.见详解
【分析】把梯形按2∶1扩大,即梯形的每一条边扩大到原来的2倍,原梯形的上底、下底和高分别乘2,得出扩大后梯形的上底、下底和高,据此画出扩大后的图形。
把长方形按1∶2缩小,即长方形的每一条边缩小到原来的,原长方形的长和宽分别除以2,得出缩小后长方形的长和宽,据此画出缩小后的图形。
【详解】如图:
【点睛】此题主要考查图形的放大与缩小,明确放大或缩小的是图形的各个边长,图形的形状不变是解题的关键。
6.见详解
【分析】三角形按2∶1放大,则把原来三角形的底和高扩大到原来的2倍,已知原来底和高分别是3格和2格,分别用3×2和2×2即可求出扩大后的底和高,据此画图。
【详解】原来底和高分别是3格和2格,
3×2=6(格)
2×2=4(格)
如图:
【点睛】本题主要考查了图形的放大,明确图形的放大只改变图形的大小,不改变图形的形状。
7.见解析
【分析】根据图上距离∶实际距离=比例尺,可得:图上距离=实际距离×比例尺。
【详解】2×10=20(毫米)
【点睛】本题主要考查了比例尺的意义的灵活应用,注意单位的换算。
8.见详解
【分析】图中已经标出向右为正方向以及2千克所在位置。2千克是正数,位于原点右边,所以原点位于2千克左边,相差2个单位长度:即“0”位于2千克向左数两格处;
“体重下降3千克”可以用“﹣3千克表示”,应位于“0”再向左数3格处。
【详解】
9.见详解
【分析】圆柱是由3个面围成的,圆柱的上、下两个面叫做底面,圆柱周围的面(上、下底面除外)叫做侧面,圆柱两个底面之间的距离叫做高,据此解答。
【详解】分析可知:
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
10.
【详解】略
11.见详解
【分析】数轴的定义,规定了原点、正方向和长度单位的直线就是数轴。
原点左边的为负数,原点右边的为正数,在数轴上的数从左到右依次变大。
就是将0到1之间的距离看成单位“1”分成4份,取其中1份。也就是1到2中间。也就是2到3中间。
【详解】
12.见详解
【分析】根据图中线段比例尺,在火神山医院北偏东50 方向截取30÷10=3个单位长度,标出角度,终点处标注出金银潭医院的位置即可。
【详解】由分析可得:
【点睛】本题考查比例尺,掌握根据方向、角度、距离确定位置的方法是解题的关键。
13.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
【详解】本题考查图形的变换、图形的缩放及轴对称图形.图形旋转注意三点:旋转点、方向和角度;图形放大和缩小关键点是对应边的放大和缩小;轴对称关键是找对称点.
(1)根据旋转的性质,先将长方形由点A引出的两条边顺时针旋转90度,由此即可确定旋转后的图形的位置与大小.(2)根据放大和缩小的性质,先把两条直角边分别缩小2倍,即可画出缩小后的三角形.(3)根据轴对称图形的定义和画指定面积的图形的方法,这里可以画一个长是10厘米、高是2厘米的等腰三角形,并画出它的对称轴.如图所示:
14.见详解
【分析】把图形按照2∶1放大,就是将图形的每一条边放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1;把图形按照1∶3缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶3。
【详解】图形如下:
15.见详解
【分析】先利用1米=100厘米,把长和宽换算单位后,再根据实际距离×比例尺=图上距离,代入数据分别求出在图上长方形菜园的长和宽,据此完成作图即可。
【详解】60米=6000厘米
45米=4500厘米
长:6000×=2(厘米)
宽:4500×=1.5(厘米)
如图:
【点睛】此题的解题关键是掌握图上距离和实际距离之间的换算。
16.见详解
【分析】根据“上北下南,左西右东”先找出学校的正西方向,小明家在此方向上的2厘米处;
小明家在学校正西方向,距学校200米,小亮家在小明家正东方向,距小明家400米,说明小亮家在学校的正东方向200米处。据此,找出学校的正东方向,小亮家在此方向上的2厘米处;
最后找到学校的正北方向,小红家在此方向上的2.5厘米处。据此作图。
【详解】如图:
17.见详解
【分析】原点左边的为负数,原点右边的为正数。小乌龟从家出发,先走了﹢200m,即向右走2格,这时小乌龟到了﹢3处,之后又走了﹣500m到达了大象家,即又向左走5格,则大象家是﹣2处;小乌龟又从大象家出发,先走了﹣200m,即向左走2格,之后又走了﹢900m,即又向右走9格,则小狗家在﹢5处。据此作图。
【详解】
18.答案见详解。
【分析】将图形按放大,就是将图形的各边分别放大到原来的4倍,将图形按缩小,就是将图形的各边分别缩小到原来的,无论是放大还是缩小,均不改变图形的形状。画出图形C后,可以通过三角形的面积公式计算出图形C的面积,再在图上画出一个与图形C面积相等的梯形即可。
【详解】
【点睛】本题主要考查了图形的放大与缩小。明确比例表示的意义是解题的关键。比如:图形A按放大,就是把图形A放大到原来的4倍;图形B按缩小,就是将图形的各边分别缩小到原来的。只有准确了解比例的意思,才能进行正确作图。
19.
【分析】根据数轴上各数的特点:右边的数总比左边的数大,据此解答。
【详解】在数轴上,比﹣3大的数都在﹣3的右边。因此画图如下:
【点睛】考查了数轴的认识,解答此题要明确:数轴上的点表示的数,右边的数总比左边的数大。
20.(1)图见详解
(2)图见详解
(3)2∶1;4∶1
【分析】(1)根据旋转的特征,将长方形ABCD绕点B逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)将长方形ABCD按2∶1放大,则原来长方形的长、宽分别乘2,据此画出放大后的长方形。
(3)根据长方形的周长=(长+宽)×2,长方形的面积=长×宽,分别求出原来和放大后长方形的周长、面积,再根据比的意义,求出放大后的长方形与原长方形周长的比、面积的比,并化简比。
【详解】(1)画出长方形ABCD绕点B逆时针旋转90°后的图形,如下图。
(2)放大后长方形的长:3×2=6
放大后长方形的宽:2×2=4
画一个长为6、宽为4的长方形,如下图。
(3)原来长方形的周长:
(3+2)×2
=5×2
=10
放大后长方形的周长:
(6+4)×2
=10×2
=20
原来长方形的面积:3×2=6
放大后长方形的面积:6×4=24
20∶10=(20÷10)∶(10÷10)=2∶1
24∶6=(24÷6)∶(6÷6)=4∶1
放大后的长方形与原长方形周长的比是2∶1,面积的比是4∶1。
21.见详解
【分析】(1)图A是平行四边形,将它的底和高按照2∶1的比例放大2倍画图即可;
(2)将图B的所有顶点,以点O为圆心,顺时针旋转90度画图;
(3)将图形C的所有点向左平移5格,再向上平移6格,连线即可;
(4)以对称轴为中线,左右对称画出左边的一半。
【详解】如下图:
【点睛】此题主要考查学生对图形放大、图形旋转、平移和对称的实际应用。
22.图见详解
【分析】根据“上北下南、左西右东”可确定图示的方向,实际距离已知,结合图上比例尺,即可求出两地的图上距离,再根据两地的方向关系,即可标出静远小学的位置。
【详解】由图可知,图上距离1厘米表示实际距离200米,
800÷200=4(厘米)
作图如下:
【点睛】此题主要考查依据方向(角度)和距离判定物体位置的方法,以及线段比例尺的意义。
23.(1)见详解
(2)1∶9
(3)1∶3
【分析】(1)图中圆的半径是1格,根据图形放大与缩小的意义,按3∶1放大后的圆的半径是3格,据此画图即可;
(2)根据圆的面积公式S=πr2分别求放大前、后圆的面积,再根据比的意义写出比,然后再化简;
(3)根据圆的周长公式C=πd分别求放大前、后圆的周长,再根据比的意义写出比,然后再化简。
【详解】(1)半径占1格,放大后占3格。如下图:
(2)(3.14×12)∶(3.14×32)
=3.14×1∶(3.14×9)
=1∶9
所以放大前与放大后两个圆的面积比是1∶9。
(3)[3.14×(1×2)]∶[3.14×(3×2)]
=[3.14×2]∶[3.14×6]
=2∶6
=(2÷2)∶(6÷2)
=1∶3
所以放大前与放大后两个圆的周长比是1∶3。
24.见详解
【分析】从正面看分为两层,底层有三个小正方形,上层有两个小正方形,分别在左右两边;
从上面看分为两排,第一排有三个小正方形,第二排有两个小正方形,靠左;
从左面看有两列,每列各有两个小正方形,据此画图即可。
【详解】
【点睛】画图时要认真观察,注意两个方面:
一要数一数看到了几个小正方形;
二要看一看这些小正方形的排列方式。
观察清楚后再在方格纸上画出来。
25.见详解
【分析】(1)先从原图形上找到关键点,再根据每个点到对称轴的距离,找到这些点关于对称轴的对称点,最后把这些点依次连接起来;
(2)找出构成图形的关键点,确定平移方向(先向右,再向上)和平移距离(先5格,再3格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点;
(3)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形;
(4)原来梯形的上底是3格,放大后上底是3×3=9格,原来梯形的下底是4格,放大后下底是4×3=12格,原来梯形的高是2格,放大后高是2×3=6格,据此作图。
【详解】作图如下:
【点睛】掌握轴对称、平移、旋转图形的作图方法并求出放大后梯形各边的格数是解答题目的关键。
26.见详解
【分析】长方形按放大,只需要数出长方形的长与宽的格数,再乘2即可画出;
三角形按放大,只要数出底与高各自的格数,然后分别乘2画出即可。
【详解】原长方形的长与宽分别是3格、2格,扩大后的长方形的长与宽分别是(格),(格)
原三角形的底和高分别是2格、2格,扩大后的三角形的底和高分别是(格),(格)
据此画图如下:
【点睛】解答本题关键是注意按放大就是把原图形的边长分别扩大2倍。
27.见详解
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。 垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高,据此分析。
【详解】
28.答案见详解。
【分析】由图意知:每一格代表1个单位。A点在负4的左边,,紧贴负4,那就是负5;B点在0和负2之间,那就是负1;C在2和4之间,那就是3。据此解答。
【详解】
【点睛】本题主要考查负数和正数的认识。能根据数轴提供的信息确定每一格代表的数量及其数的正负,是解答本题的关键。
29.
【详解】略
30.见解析
【详解】试题分析:根据高一定时,三角形的面积与底成正比的关系,把三角形的高定为梯形的高,底按照1:2:3进行划分即可解答.
解:根据题干分析,可将这个梯形划分为如图所示的三个三角形,使它们的面积之比为1:2:3,
.
点评:此题考查了高一定时,三角形的面积与高成正比关系的灵活应用.
31.
【详解】略
32.
【详解】240m=24000cm,120m=12000cm
24000×=6(cm)
12000×=3(cm)
即画长方形运动场的长是6cm,宽是3cm.
33.如图
【分析】(1)根据数对表示位置的方法,先在平面图中标出各点的位置,再依次连接起来得出三角形ABC;
(2)根据图形平移的方法,把三角形ABC的三个顶点分别向下平移5格,再依次连接起来即可得出平移后的三角形1;
(3)根据图形缩小的方法,先数出原三角形的底是4格,高是2格,再把它们除以2,即可得出缩小的三角形的底是2格,高是1格,据此以点A′为顶点,即可画出缩小后的三角形2;
(4)根据图形旋转的方法,把正方形的另外三个顶点,分别绕点O顺时针旋转180°后得出旋转后的三个对应顶点,再依次连接起来得出旋转后的正方形与原正方形组成一个轴对称图形,再根据轴对称图形的性质,即可画出它们的对称轴。
【详解】根据题干分析,画图如下:
【点睛】此题主要考查数对表示位置的方法和利用图形的旋转、平移、放大与缩小、以及轴对称图形的性质,进行图形变换的方法的灵活应用。
34.(1)A(0,4)、B(2,6)、C(2,4)
(2)图见详解;
(3)图见详解;
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对表示A、B、C三点的位置。
(2)根据旋转的特征,三角形ABC绕点C顺时针旋转180度,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)由于直角三角形两直角边即可确定其形状,根据图形放大的意义,把这个三角形两直角边均放大到原来的2倍,所得到的图形就是旋转后按2∶1扩大后的图形。
【详解】(1)A(0,4)、B(2,6)、C(2,4)
(2)如图:
(3)如图:
【点睛】此题考查了数对与位置、作旋转一定度数后的图形、图形的放大与缩小。
35.如下图:
【详解】略
36.见详解
【分析】根据图上距离=实际距离×比例尺,代入数据,分别求出小梅家到学校的图上距离;小方家到学校的距离,再根据地图上方向的规定“上北下南,左西右东”,以学校为观测点,画出小梅家和小方家位置,即可解答。
【详解】300米=30000厘米
400米=40000厘米
30000÷20000=1.5(厘米)
40000÷20000=2(厘米)
如题:
37.见详解
【分析】圆柱是由3个面围成的,圆柱的上、下两个面叫做底面,圆柱周围的面(上、下底面除外)叫做侧面,圆柱两个底面之间的距离叫做高,据此解答。
【详解】如图所示:
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
38.
【详解】观察图可知,图中是按“上北下南,左西右东”来规定方向的,图中1厘米表示实际距离50米,以教学楼为观测点,根据方向和距离找到大门和图书馆的位置,据此作图.
39.见详解
【分析】(1)20000厘米=200米,先把数值比例尺转化为线段比例尺,图上1厘米代表实际距离200米,1千米=1000米,再以学校为观测点,在学校正西方向偏北40°上截取1000÷200=5厘米,标出角度,终点处标注琪琪家;
(2)直线外一点到直线的连线中垂线段最短,把三角尺的一条直角边与畅家巷所在的直线重合,沿着直线移动三角尺,使琪琪家在三角尺的另一条直角边上,沿三角尺的另一条直角边画出最短线段,并画出垂直符号,据此解答。
【详解】(1)(2)分析可知:
【点睛】掌握根据方向、角度、距离确定物体位置的方法和过直线外一点作已知直线的垂线的方法是解答题目的关键。
40.
【分析】
方向和距离两个条件才能确定物体的位置,要画图首先要根据图形确定比例尺为1:10000,和方向上北下南左西右东。(1)健康路在市政府东面,可确定其方向,根据图上距=实际距离×比例尺,求出市政府到健康路图上距离。(2)育才小学在市政府北偏西75°,可确定其方向,再根据图上距离=实际距离×比例尺,可求出其图上距离,据此画图解答.本题的关键是确定比例尺和方向后,根据图上距离=实际距离×比例尺,求出图上距离,再画图解答。
【详解】(1)健康路到市政府的图上距离是:
300米=30000厘米
30000× =3(厘米)
(2)育才小学到市政府的图上距离是:
400米=40000厘米
40000× =4(厘米)
画图如下:
41.
【详解】先找到大三角形底边的中点,顶点和中点相连;再找到大三角形左右两边的中点,底边的中点和左右两边的中点相连,总之,图中线段中间的点,都是中点。这样分出的三角形等底等高,面积都相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
人教版六年级下册数学期末专项训练:作图题
学校:___________姓名:___________班级:___________考号:___________
一、作图题
1.把下面图1的图形每边放大到原来的2倍,把图2的图形每边缩小到原来的.
2.先按4∶1把下面的三角形放大,再把放大后的图形按1∶2缩小。
3.按1∶4画出三角形缩小后的图形。
4.用圆规和三角尺画出下面的图案。你还能设计什么图案?
5.按2∶1画出梯形放大后的图形,按1∶2画出长方形缩小后的图形。
6.按2∶1画出下面图形放大后的图形。
7.一个圆形零件的直径是2毫米。请你用10∶1的比例尺画出这个零件的平面图。
8.请在数轴上恰当位置表示出“0”和“体重下降3千克”记作的数。
9.标出下面圆柱的底面、侧面和高。
10.画一个半径为1cm的圆,并标出圆心、半径.
11.在直线上表示下面各数。
12.为与新冠病毒竞速,武汉市火速建设了雷神山、火神山医院,以集中收治肺炎患者。火神山医院的建成,可大大缓解北偏东50 方向30千米处的金银潭医院的就诊压力,请在图中标出金银潭医院的位置。
13.(1)把图中的长方形绕A点顺时针旋转90°,画出旋转后的图形.
(2)按1:2的比画出三角形缩小后的图形,缩小后的三角形的面积是原来的( ).
(3)如果一个小方格表示1平方厘米,在方格纸上设计一个面积是10平方厘米的轴对称图形,并画出对称轴.
14.画出下面平行四边形按放大后的图形,再画出下面梯形按缩小后的图形。
15.王奶奶家有一个长60米,宽45米的长方形菜园。请在下面图中画出这个菜园的平面图(比例尺1∶3000)。
16.小明家在学校正西方向,距学校200米;小亮家在小明家正东方向,距小明家400米;小红家在学校正北方向,距学校250米。在下图中画出他们三家和学校的位置平面图(比例尺1∶10000)。
想:先求出每家到学校的图上距离。根据“”,得到“图上距离=实际距离×比例尺”。
200米=20000厘米,400米=40000厘米,250米=25000厘米
小明家到学校的图上距离:(厘米)
小亮家到学校的图上距离:(厘米)
小红家到学校的图上距离:(厘米)
17.直线上每格代表100m,小乌龟的家在﹢1处。
①小乌龟从家出发,先走了﹢200m,之后又走了﹣500m到达了大象家。请用“△”标出大象家的位置。
②小乌龟又从大象家出发,先走了﹣200m,之后又走了﹢900m到达小狗家。请用“○”标出小狗家的位置。
18.按要求画图。
(1)画出图形A按放大后的图形B。
(2)画出图形B按缩小后的图形C。
(3)画出一个与图形C面积相等的梯形。
19.在下面直线上,画出比-3大的数所在区域。
20.(1)画出长方形ABCD绕点B逆时针旋转90°后的图形。
(2)将长方形ABCD按2∶1放大后画在合适的位置。
(3)观察并思考,放大后的长方形与原长方形周长的比是( ),面积的比是( )。
21.
(1)画出图形A按2∶1放大后的图形。
(2)把图形B绕点O顺时针旋转90°。
(3)把图形C先向左平移5格,再向上平移6格,画出最终得到的图形。
(4)画出图形D的另一半,使它成为一个轴对称图形。
22.随着镇海区静远小学的落成和地铁7号线的建设,镇海新城发展的脚步越来越快。静远小学在西大河足球场的东偏北40°方向800米的位置,请在下面的平面图中画出静远小学的位置。
23.操作。
(1)以O点为中心,按3∶1的比画出放大后的图形。
(2)放大前与放大后两个圆的面积比是( )。
(3)放大前与放大后两个圆的周长比是( )。
24.小红用若干个相同的小正方体摆了一个立体图形(如下图),在下面方格纸上分别画出从它的正面、上面和左面看到的形状。
25.按要求完成下面各题。
(1)画出图A的另一半,使它成为一个轴对称图形。
(2)把图B向右平移5格,再向上平移3格。
(3)把图C绕点O逆时针旋转90°。
(4)把图D按3∶1放大。
26.按的比画出下面图形放大后的图形。
27.指出下面圆锥的底面、侧面和高。
28.写出点A、B、C表示的数。
29.画出下面各个图形指定底边上的高.
30.将方格里的梯形面积按1:2:3分成三个三角形.
31.按3:1画出下面三个图形放大后的图形.
32.某市新建一个长方形运动场,长240m,宽120m,请在下面图中画出运动场的平面图.(比例尺:1:4000)
33.按要求完成。
(1)在如图中描出下面各点,并依此连成一个三角形;A(2,7)、B(6,7)、C(4,9)
(2)画出三角形向下平移5格后的图形;
(3)将三角形缩小为原来的,画在右边,要求点A画在A′上;
(4)画出正方形绕O点顺时针旋转180°后的图形,这时两个正方形组成了一个新图形,画出新图形的其中一条对称轴。
34.根据要求在下图中操作,并回答问题。
一只蚂蚁从点A沿东北方向爬到点B,又沿正南方向到点C,最后沿正西方向返回到A点。
(1)用数对表示A( )、B( )、C( )的位置。
(2)将三角形ABC沿点C顺时针方向旋转180度,画出旋转后的图形。
(3)画出旋转后按2∶1扩大的图形。
35.画一个圆锥,标出它的底面半径和高.
36.在下图中标出他们两家的位置。
37.指出下面圆柱的底面、侧面和高。
38.实验小学大门在教学楼的正南方向50米处,图书馆在教学楼的北偏东60°方向100米处.在下图中表示出大门和图书馆的位置.
39.(1)琪琪家在学校西偏北40°方向,距离学校1千米,请在下图中用“●”表示出琪琪家的位置。
(2)在下图中画出琪琪家到畅家巷的最短线段。
40.下面是仪征城区的平面图,请在图中画出有关街道和场所的位置。
(1)市政府东面300米的处有一条健康路,它与工农路平行。
(2)育才小学在市政府北偏西75°方向400米处。
41.下面三角形图中8个字.请你用笔画上6条线,将八卦巧分8块,每块形状是大小相等的三角形。
《人教版六年级下册数学期末专项训练:作图题》参考答案
1.
【详解】解:
分析:(1)把图①中各条边的长度扩大2倍,据此画出;
(2)把图②中各条边的长度缩小2倍,据此画出.
2.
【分析】按4∶1放大,就是把新图形的每条边长扩大到原来的4倍;按1∶2缩小,就是把新图形的每条边长缩小为原来的。
【详解】这是一个直角三角形,底2高1,按4∶1扩大后,底8高4;再按1∶2缩小,就是底4高2。
【点睛】通常把比例尺写成前项(或后项)为1的比,图上距离为前项,实际距离为后项,掌握好这些,作图就不难了。
3.见详解
【分析】把三角形按1∶4缩小,即三角形的每一条边缩小到原来的,原三角形的底和高分别除以4,得出缩小后三角形的底和高,据此画出缩小后的图形。
【详解】如图:
【点睛】本题考查图形的放大或缩小,明确放大或缩小的是图形的各个边长,图形的形状不变是解题的关键。
4.见详解
【分析】画图(1)只需要圆规:首先确定大圆圆心的位置,再以2厘米(不唯一)作为半径画出大圆,然后在大圆中画出两条互相垂直的直径(共4条半径),在每条半径的中点以1厘米(大圆半径的一半)为半径分别画出4个小圆。
画图(2)需要用到圆规和三角尺:同样先确定大圆的圆心,以2厘米(不唯一)为半径画出大圆,在大圆中画出三条直径,直径两两之间的夹角为60度,此时直径与圆形成6个交点,将其中三个相间隔的交点两两连接。
图案设计可自由发挥,合理即可。
【详解】画上图:
设计图案(答案不唯一):
5.见详解
【分析】把梯形按2∶1扩大,即梯形的每一条边扩大到原来的2倍,原梯形的上底、下底和高分别乘2,得出扩大后梯形的上底、下底和高,据此画出扩大后的图形。
把长方形按1∶2缩小,即长方形的每一条边缩小到原来的,原长方形的长和宽分别除以2,得出缩小后长方形的长和宽,据此画出缩小后的图形。
【详解】如图:
【点睛】此题主要考查图形的放大与缩小,明确放大或缩小的是图形的各个边长,图形的形状不变是解题的关键。
6.见详解
【分析】三角形按2∶1放大,则把原来三角形的底和高扩大到原来的2倍,已知原来底和高分别是3格和2格,分别用3×2和2×2即可求出扩大后的底和高,据此画图。
【详解】原来底和高分别是3格和2格,
3×2=6(格)
2×2=4(格)
如图:
【点睛】本题主要考查了图形的放大,明确图形的放大只改变图形的大小,不改变图形的形状。
7.见解析
【分析】根据图上距离∶实际距离=比例尺,可得:图上距离=实际距离×比例尺。
【详解】2×10=20(毫米)
【点睛】本题主要考查了比例尺的意义的灵活应用,注意单位的换算。
8.见详解
【分析】图中已经标出向右为正方向以及2千克所在位置。2千克是正数,位于原点右边,所以原点位于2千克左边,相差2个单位长度:即“0”位于2千克向左数两格处;
“体重下降3千克”可以用“﹣3千克表示”,应位于“0”再向左数3格处。
【详解】
9.见详解
【分析】圆柱是由3个面围成的,圆柱的上、下两个面叫做底面,圆柱周围的面(上、下底面除外)叫做侧面,圆柱两个底面之间的距离叫做高,据此解答。
【详解】分析可知:
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
10.
【详解】略
11.见详解
【分析】数轴的定义,规定了原点、正方向和长度单位的直线就是数轴。
原点左边的为负数,原点右边的为正数,在数轴上的数从左到右依次变大。
就是将0到1之间的距离看成单位“1”分成4份,取其中1份。也就是1到2中间。也就是2到3中间。
【详解】
12.见详解
【分析】根据图中线段比例尺,在火神山医院北偏东50 方向截取30÷10=3个单位长度,标出角度,终点处标注出金银潭医院的位置即可。
【详解】由分析可得:
【点睛】本题考查比例尺,掌握根据方向、角度、距离确定位置的方法是解题的关键。
13.(1)
(2)如图,﹙2×1.5÷2﹚÷﹙4×3÷2﹚=
(3)如图,答案不唯一.
【详解】本题考查图形的变换、图形的缩放及轴对称图形.图形旋转注意三点:旋转点、方向和角度;图形放大和缩小关键点是对应边的放大和缩小;轴对称关键是找对称点.
(1)根据旋转的性质,先将长方形由点A引出的两条边顺时针旋转90度,由此即可确定旋转后的图形的位置与大小.(2)根据放大和缩小的性质,先把两条直角边分别缩小2倍,即可画出缩小后的三角形.(3)根据轴对称图形的定义和画指定面积的图形的方法,这里可以画一个长是10厘米、高是2厘米的等腰三角形,并画出它的对称轴.如图所示:
14.见详解
【分析】把图形按照2∶1放大,就是将图形的每一条边放大到原来的2倍,放大后图形与原图形对应边长的比是2∶1;把图形按照1∶3缩小,就是将图形的每一条边缩小到原来的,缩小后图形与原图形对应边长的比是1∶3。
【详解】图形如下:
15.见详解
【分析】先利用1米=100厘米,把长和宽换算单位后,再根据实际距离×比例尺=图上距离,代入数据分别求出在图上长方形菜园的长和宽,据此完成作图即可。
【详解】60米=6000厘米
45米=4500厘米
长:6000×=2(厘米)
宽:4500×=1.5(厘米)
如图:
【点睛】此题的解题关键是掌握图上距离和实际距离之间的换算。
16.见详解
【分析】根据“上北下南,左西右东”先找出学校的正西方向,小明家在此方向上的2厘米处;
小明家在学校正西方向,距学校200米,小亮家在小明家正东方向,距小明家400米,说明小亮家在学校的正东方向200米处。据此,找出学校的正东方向,小亮家在此方向上的2厘米处;
最后找到学校的正北方向,小红家在此方向上的2.5厘米处。据此作图。
【详解】如图:
17.见详解
【分析】原点左边的为负数,原点右边的为正数。小乌龟从家出发,先走了﹢200m,即向右走2格,这时小乌龟到了﹢3处,之后又走了﹣500m到达了大象家,即又向左走5格,则大象家是﹣2处;小乌龟又从大象家出发,先走了﹣200m,即向左走2格,之后又走了﹢900m,即又向右走9格,则小狗家在﹢5处。据此作图。
【详解】
18.答案见详解。
【分析】将图形按放大,就是将图形的各边分别放大到原来的4倍,将图形按缩小,就是将图形的各边分别缩小到原来的,无论是放大还是缩小,均不改变图形的形状。画出图形C后,可以通过三角形的面积公式计算出图形C的面积,再在图上画出一个与图形C面积相等的梯形即可。
【详解】
【点睛】本题主要考查了图形的放大与缩小。明确比例表示的意义是解题的关键。比如:图形A按放大,就是把图形A放大到原来的4倍;图形B按缩小,就是将图形的各边分别缩小到原来的。只有准确了解比例的意思,才能进行正确作图。
19.
【分析】根据数轴上各数的特点:右边的数总比左边的数大,据此解答。
【详解】在数轴上,比﹣3大的数都在﹣3的右边。因此画图如下:
【点睛】考查了数轴的认识,解答此题要明确:数轴上的点表示的数,右边的数总比左边的数大。
20.(1)图见详解
(2)图见详解
(3)2∶1;4∶1
【分析】(1)根据旋转的特征,将长方形ABCD绕点B逆时针旋转90°,点B位置不变,其余各部分均绕此点按相同方向旋转相同度数,即可画出旋转后的图形。
(2)将长方形ABCD按2∶1放大,则原来长方形的长、宽分别乘2,据此画出放大后的长方形。
(3)根据长方形的周长=(长+宽)×2,长方形的面积=长×宽,分别求出原来和放大后长方形的周长、面积,再根据比的意义,求出放大后的长方形与原长方形周长的比、面积的比,并化简比。
【详解】(1)画出长方形ABCD绕点B逆时针旋转90°后的图形,如下图。
(2)放大后长方形的长:3×2=6
放大后长方形的宽:2×2=4
画一个长为6、宽为4的长方形,如下图。
(3)原来长方形的周长:
(3+2)×2
=5×2
=10
放大后长方形的周长:
(6+4)×2
=10×2
=20
原来长方形的面积:3×2=6
放大后长方形的面积:6×4=24
20∶10=(20÷10)∶(10÷10)=2∶1
24∶6=(24÷6)∶(6÷6)=4∶1
放大后的长方形与原长方形周长的比是2∶1,面积的比是4∶1。
21.见详解
【分析】(1)图A是平行四边形,将它的底和高按照2∶1的比例放大2倍画图即可;
(2)将图B的所有顶点,以点O为圆心,顺时针旋转90度画图;
(3)将图形C的所有点向左平移5格,再向上平移6格,连线即可;
(4)以对称轴为中线,左右对称画出左边的一半。
【详解】如下图:
【点睛】此题主要考查学生对图形放大、图形旋转、平移和对称的实际应用。
22.图见详解
【分析】根据“上北下南、左西右东”可确定图示的方向,实际距离已知,结合图上比例尺,即可求出两地的图上距离,再根据两地的方向关系,即可标出静远小学的位置。
【详解】由图可知,图上距离1厘米表示实际距离200米,
800÷200=4(厘米)
作图如下:
【点睛】此题主要考查依据方向(角度)和距离判定物体位置的方法,以及线段比例尺的意义。
23.(1)见详解
(2)1∶9
(3)1∶3
【分析】(1)图中圆的半径是1格,根据图形放大与缩小的意义,按3∶1放大后的圆的半径是3格,据此画图即可;
(2)根据圆的面积公式S=πr2分别求放大前、后圆的面积,再根据比的意义写出比,然后再化简;
(3)根据圆的周长公式C=πd分别求放大前、后圆的周长,再根据比的意义写出比,然后再化简。
【详解】(1)半径占1格,放大后占3格。如下图:
(2)(3.14×12)∶(3.14×32)
=3.14×1∶(3.14×9)
=1∶9
所以放大前与放大后两个圆的面积比是1∶9。
(3)[3.14×(1×2)]∶[3.14×(3×2)]
=[3.14×2]∶[3.14×6]
=2∶6
=(2÷2)∶(6÷2)
=1∶3
所以放大前与放大后两个圆的周长比是1∶3。
24.见详解
【分析】从正面看分为两层,底层有三个小正方形,上层有两个小正方形,分别在左右两边;
从上面看分为两排,第一排有三个小正方形,第二排有两个小正方形,靠左;
从左面看有两列,每列各有两个小正方形,据此画图即可。
【详解】
【点睛】画图时要认真观察,注意两个方面:
一要数一数看到了几个小正方形;
二要看一看这些小正方形的排列方式。
观察清楚后再在方格纸上画出来。
25.见详解
【分析】(1)先从原图形上找到关键点,再根据每个点到对称轴的距离,找到这些点关于对称轴的对称点,最后把这些点依次连接起来;
(2)找出构成图形的关键点,确定平移方向(先向右,再向上)和平移距离(先5格,再3格),由平移的距离确定关键点平移后的对应点的位置,依次连接各对应点;
(3)根据题目要求确定旋转中心(点O)、旋转方向(逆时针)、旋转角度(90°),分析所作图形,找出构成图形的关键边,按一定的方向和角度分别找出各关键边的对应边,最后依次连接组成封闭图形;
(4)原来梯形的上底是3格,放大后上底是3×3=9格,原来梯形的下底是4格,放大后下底是4×3=12格,原来梯形的高是2格,放大后高是2×3=6格,据此作图。
【详解】作图如下:
【点睛】掌握轴对称、平移、旋转图形的作图方法并求出放大后梯形各边的格数是解答题目的关键。
26.见详解
【分析】长方形按放大,只需要数出长方形的长与宽的格数,再乘2即可画出;
三角形按放大,只要数出底与高各自的格数,然后分别乘2画出即可。
【详解】原长方形的长与宽分别是3格、2格,扩大后的长方形的长与宽分别是(格),(格)
原三角形的底和高分别是2格、2格,扩大后的三角形的底和高分别是(格),(格)
据此画图如下:
【点睛】解答本题关键是注意按放大就是把原图形的边长分别扩大2倍。
27.见详解
【分析】以直角三角形的直角边所在直线为旋转轴,其余两边旋转360度而成的曲面所围成的几何体叫做圆锥。旋转轴叫做圆锥的轴。 垂直于轴的边旋转而成的曲面叫做圆锥的底面。不垂直于轴的边旋转而成的曲面叫做圆锥的侧面。圆锥的顶点到圆锥的底面圆心之间的最短距离叫做圆锥的高,据此分析。
【详解】
28.答案见详解。
【分析】由图意知:每一格代表1个单位。A点在负4的左边,,紧贴负4,那就是负5;B点在0和负2之间,那就是负1;C在2和4之间,那就是3。据此解答。
【详解】
【点睛】本题主要考查负数和正数的认识。能根据数轴提供的信息确定每一格代表的数量及其数的正负,是解答本题的关键。
29.
【详解】略
30.见解析
【详解】试题分析:根据高一定时,三角形的面积与底成正比的关系,把三角形的高定为梯形的高,底按照1:2:3进行划分即可解答.
解:根据题干分析,可将这个梯形划分为如图所示的三个三角形,使它们的面积之比为1:2:3,
.
点评:此题考查了高一定时,三角形的面积与高成正比关系的灵活应用.
31.
【详解】略
32.
【详解】240m=24000cm,120m=12000cm
24000×=6(cm)
12000×=3(cm)
即画长方形运动场的长是6cm,宽是3cm.
33.如图
【分析】(1)根据数对表示位置的方法,先在平面图中标出各点的位置,再依次连接起来得出三角形ABC;
(2)根据图形平移的方法,把三角形ABC的三个顶点分别向下平移5格,再依次连接起来即可得出平移后的三角形1;
(3)根据图形缩小的方法,先数出原三角形的底是4格,高是2格,再把它们除以2,即可得出缩小的三角形的底是2格,高是1格,据此以点A′为顶点,即可画出缩小后的三角形2;
(4)根据图形旋转的方法,把正方形的另外三个顶点,分别绕点O顺时针旋转180°后得出旋转后的三个对应顶点,再依次连接起来得出旋转后的正方形与原正方形组成一个轴对称图形,再根据轴对称图形的性质,即可画出它们的对称轴。
【详解】根据题干分析,画图如下:
【点睛】此题主要考查数对表示位置的方法和利用图形的旋转、平移、放大与缩小、以及轴对称图形的性质,进行图形变换的方法的灵活应用。
34.(1)A(0,4)、B(2,6)、C(2,4)
(2)图见详解;
(3)图见详解;
【分析】(1)根据用数对表示点的位置的方法,第一个数字表示列,第二个数字表示行,即可用数对表示A、B、C三点的位置。
(2)根据旋转的特征,三角形ABC绕点C顺时针旋转180度,点C的位置不动,这个图形的各部分均绕此点按相同方向旋转相同的度数即可画出旋转后的图形。
(3)由于直角三角形两直角边即可确定其形状,根据图形放大的意义,把这个三角形两直角边均放大到原来的2倍,所得到的图形就是旋转后按2∶1扩大后的图形。
【详解】(1)A(0,4)、B(2,6)、C(2,4)
(2)如图:
(3)如图:
【点睛】此题考查了数对与位置、作旋转一定度数后的图形、图形的放大与缩小。
35.如下图:
【详解】略
36.见详解
【分析】根据图上距离=实际距离×比例尺,代入数据,分别求出小梅家到学校的图上距离;小方家到学校的距离,再根据地图上方向的规定“上北下南,左西右东”,以学校为观测点,画出小梅家和小方家位置,即可解答。
【详解】300米=30000厘米
400米=40000厘米
30000÷20000=1.5(厘米)
40000÷20000=2(厘米)
如题:
37.见详解
【分析】圆柱是由3个面围成的,圆柱的上、下两个面叫做底面,圆柱周围的面(上、下底面除外)叫做侧面,圆柱两个底面之间的距离叫做高,据此解答。
【详解】如图所示:
【点睛】本题主要考查圆柱的认识,掌握圆柱的特征是解答题目的关键。
38.
【详解】观察图可知,图中是按“上北下南,左西右东”来规定方向的,图中1厘米表示实际距离50米,以教学楼为观测点,根据方向和距离找到大门和图书馆的位置,据此作图.
39.见详解
【分析】(1)20000厘米=200米,先把数值比例尺转化为线段比例尺,图上1厘米代表实际距离200米,1千米=1000米,再以学校为观测点,在学校正西方向偏北40°上截取1000÷200=5厘米,标出角度,终点处标注琪琪家;
(2)直线外一点到直线的连线中垂线段最短,把三角尺的一条直角边与畅家巷所在的直线重合,沿着直线移动三角尺,使琪琪家在三角尺的另一条直角边上,沿三角尺的另一条直角边画出最短线段,并画出垂直符号,据此解答。
【详解】(1)(2)分析可知:
【点睛】掌握根据方向、角度、距离确定物体位置的方法和过直线外一点作已知直线的垂线的方法是解答题目的关键。
40.
【分析】
方向和距离两个条件才能确定物体的位置,要画图首先要根据图形确定比例尺为1:10000,和方向上北下南左西右东。(1)健康路在市政府东面,可确定其方向,根据图上距=实际距离×比例尺,求出市政府到健康路图上距离。(2)育才小学在市政府北偏西75°,可确定其方向,再根据图上距离=实际距离×比例尺,可求出其图上距离,据此画图解答.本题的关键是确定比例尺和方向后,根据图上距离=实际距离×比例尺,求出图上距离,再画图解答。
【详解】(1)健康路到市政府的图上距离是:
300米=30000厘米
30000× =3(厘米)
(2)育才小学到市政府的图上距离是:
400米=40000厘米
40000× =4(厘米)
画图如下:
41.
【详解】先找到大三角形底边的中点,顶点和中点相连;再找到大三角形左右两边的中点,底边的中点和左右两边的中点相连,总之,图中线段中间的点,都是中点。这样分出的三角形等底等高,面积都相等。
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
