【期末章节复习】分式(含答案)-2024-2025学年数学八年级下册苏科版
文档属性
| 名称 | 【期末章节复习】分式(含答案)-2024-2025学年数学八年级下册苏科版 |  | |
| 格式 | docx | ||
| 文件大小 | 401.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 18:10:48 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末章节复习】分式-2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2025 中山市三模)若分式的值等于0,则a的值为( )
A.±1 B.0 C.﹣1 D.1
2.(2024秋 长沙期末)把分式中的x,y的值都扩大为原来的3倍,则分式的值( )
A.缩小为原来的 B.不变
C.扩大为原来的6倍 D.扩大为原来的3倍
3.(2025春 小店区校级月考)下列各式中最简分式是( )
A. B.
C. D.
4.(2025春 郑州月考)若关于x的分式方程有增根,则a的值为( )
A.1 B.2 C.3 D.4
5.(2025春 万州区月考)如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A.扩大到原来的2倍 B.扩大到原来的4倍
C.不变 D.缩小到原来的
6.(2025 福田区校级三模)我国古代数学著作《九章算术》中有一道关于“驿站送信”的题目,其大意为:把一封信送到800里外的地方,若用慢马送,则晚1天送达;若用快马送则早3天送达,已知快马的速度是慢马速度的2倍,问规定的时间为多少天?快马的速度为多少?下列说法错误的是( )
A.设规定的时间为x天,所列方程为
B.规定的时间为7天
C.设慢马的速度为y里/天,所列方程为
D.快马速度是200里/天
7.(2025 福建模拟)随着无人机技术的发展,无人机表演越来越受欢迎.在一次无人机表演排练时,A无人机落后B无人机30米,已知B无人机的飞行速度为3米/秒,若A无人机飞行200米刚好追上B无人机,设A无人机接下来的飞行速度为x米/秒,则下列方程正确的是( )
A. B.
C. D.
8.(2025春 小店区校级月考)某地响应“绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”打造美好家园.某工程队承接了60万平方米的荒山绿化工程,由于情况有变…设原计划每天绿化的面积为x万平方米,列方程为.根据方程在题干中省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了25%,结果延误8天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了25%,结果延误8天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了25%,结果提前8天完成了这一任务
二.填空题(共6小题)
9.(2025 南京三模)使式子有意义的x的取值范围是 .
10.(2025 福建模拟)已知非零实数a,b满足,且a≠b,则的值等于 .
11.(2025 凉山州)若关于x的分式方程3无解,则m= .
12.(2025春 温江区校级月考)已知:a+2b=2025,则分式 .
13.(2025春 南岸区期中)若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 .
14.(2025春 奉贤区月考)用换元法解分式方程,如果设y=x2﹣x,那么原方程可化为关于y的整式方程是 .
三.解答题(共6小题)
15.(2025 晋江市模拟)解分式方程:.
16.(2025 昭通模拟)先化简,再求值(a+2),其中a=﹣2.
17.(2025 楚雄州模拟)本着低碳出行与强身健体的理念,赵老师决定改骑共享单车上下班.通过一段时间的体验,赵老师发现每天上班所用时间只比自驾车多0.3小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是骑共享单车速度的2倍,求赵老师骑共享单车每小时行驶多少千米.
18.(2025 怒江州模拟)云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
19.(2024秋 荣昌区期末)为激励同学们参与数学阅读,罗老师准备购买两种不同的笔记本奖励给部分同学.已知A种笔记本的单价比B种笔记本单价多2元,他花50元购买A种笔记本数量与花40元购买B种笔记本数量相同.
(1)A,B两种笔记本的单价各是多少元?
(2)罗老师在购买的时候,决定对全班50名同学进行奖励,每人奖一个笔记本,A种笔记本作为一等奖奖品,B种笔记本作为二等奖奖品,一等奖人数不少于二等奖人数的一半,罗老师所带现金共440元,在使用仅有现金的情况下,他购买A,B两种笔记本共有多少种可能的方案?请写出所有可能的购买方案.
20.(2025 广州二模)
背景 随着我国科技事业的不断发展,国产无人机越来越多应用于实际生活,为人们的生活带来了便利.
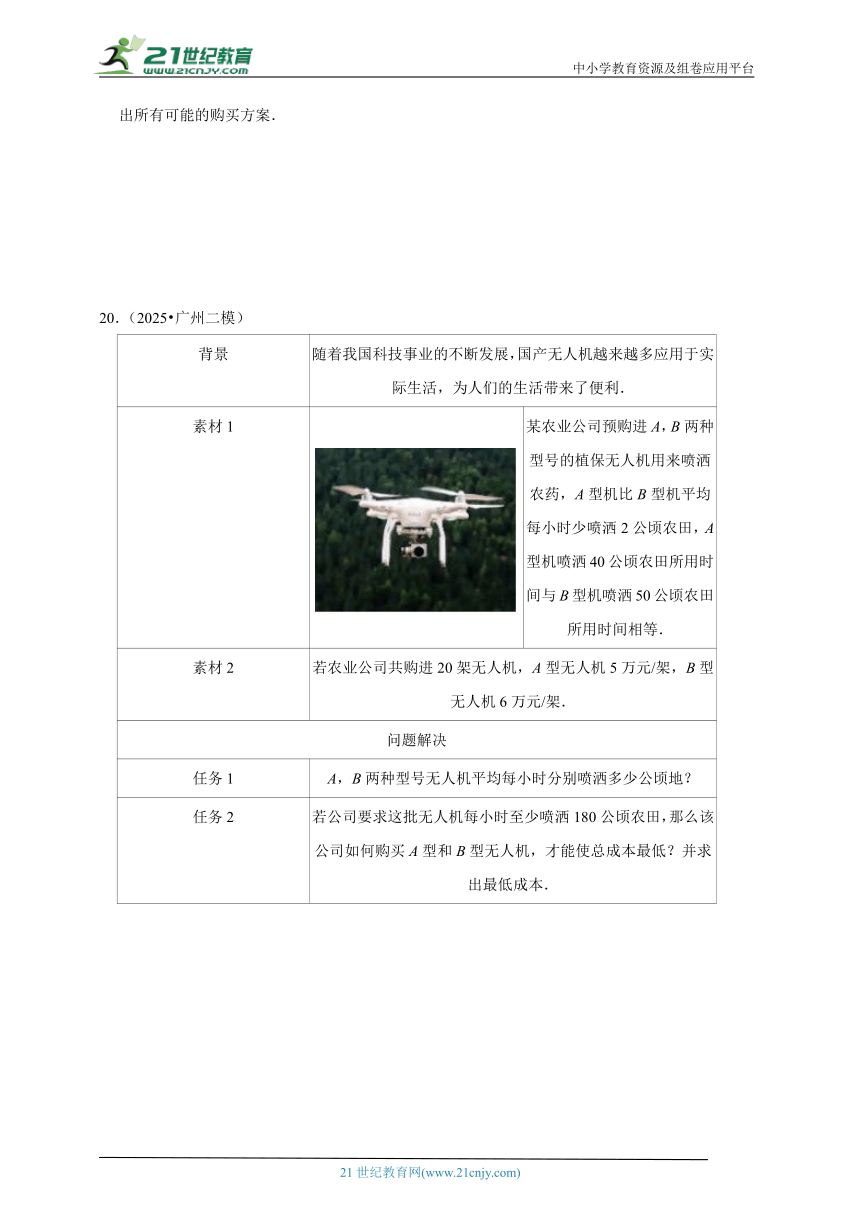
素材1
某农业公司预购进A,B两种型号的植保无人机用来喷洒农药,A型机比B型机平均每小时少喷洒2公顷农田,A型机喷洒40公顷农田所用时间与B型机喷洒50公顷农田所用时间相等.
素材2 若农业公司共购进20架无人机,A型无人机5万元/架,B型无人机6万元/架.
问题解决
任务1 A,B两种型号无人机平均每小时分别喷洒多少公顷地?
任务2 若公司要求这批无人机每小时至少喷洒180公顷农田,那么该公司如何购买A型和B型无人机,才能使总成本最低?并求出最低成本.
【期末章节复习】分式-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B D C B C A A
一.选择题(共8小题)
1.(2025 中山市三模)若分式的值等于0,则a的值为( )
A.±1 B.0 C.﹣1 D.1
【解答】解:∵分式的值等于0,
∴a﹣1=0且a+1≠0,
解得:a=1.
故选:D.
2.(2024秋 长沙期末)把分式中的x,y的值都扩大为原来的3倍,则分式的值( )
A.缩小为原来的 B.不变
C.扩大为原来的6倍 D.扩大为原来的3倍
【解答】解:由题意得:,
∴把分式中的x,y的值都扩大为原来的3倍,则分式的值不变,
故选:B.
3.(2025春 小店区校级月考)下列各式中最简分式是( )
A. B.
C. D.
【解答】解:A. ,不是最简分式,故不符合题意;
B. ,不是最简分式,故不符合题意;
C. a+1,不是最简分式,故不符合题意;
D. 是最简分式,故符合题意;
故选:D.
4.(2025春 郑州月考)若关于x的分式方程有增根,则a的值为( )
A.1 B.2 C.3 D.4
【解答】解:两边都乘以x﹣2得,a+2(x﹣2)=x+1,
由于分式方程的增根为x=2,
当x=2时,即a+0=2+1,
即a=3.
故选:C.
5.(2025春 万州区月考)如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A.扩大到原来的2倍 B.扩大到原来的4倍
C.不变 D.缩小到原来的
【解答】解:根据分式的基本性质可得:
,
∴如果把分式中的x和y都扩大为原来的4倍,那么分式的值扩大为原来的4倍,
故选:B.
6.(2025 福田区校级三模)我国古代数学著作《九章算术》中有一道关于“驿站送信”的题目,其大意为:把一封信送到800里外的地方,若用慢马送,则晚1天送达;若用快马送则早3天送达,已知快马的速度是慢马速度的2倍,问规定的时间为多少天?快马的速度为多少?下列说法错误的是( )
A.设规定的时间为x天,所列方程为
B.规定的时间为7天
C.设慢马的速度为y里/天,所列方程为
D.快马速度是200里/天
【解答】解:A、设规定时间为x天,则慢马用时(x+1)天,快马用时(x﹣3)天,
由题意得:,故选项A不符合题意;
解得:x=7,
经检验,x=7是原方程的解,且符合题意,故选项B不符合题意;
C、设慢马的速度为y里/天,则快马的速度为2y里/天,
由题意得:4,故选项C符合题意;
D、快马用了7﹣3=4天送达,速度为800÷4=200(里/天),故选项D不符合题意;
故选:C.
7.(2025 福建模拟)随着无人机技术的发展,无人机表演越来越受欢迎.在一次无人机表演排练时,A无人机落后B无人机30米,已知B无人机的飞行速度为3米/秒,若A无人机飞行200米刚好追上B无人机,设A无人机接下来的飞行速度为x米/秒,则下列方程正确的是( )
A. B.
C. D.
【解答】解:根据题意得:.
故选:A.
8.(2025春 小店区校级月考)某地响应“绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”打造美好家园.某工程队承接了60万平方米的荒山绿化工程,由于情况有变…设原计划每天绿化的面积为x万平方米,列方程为.根据方程在题干中省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了25%,结果延误8天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了25%,结果延误8天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了25%,结果提前8天完成了这一任务
【解答】解:方程为,
∴提高工作效率后比原计划提前8天完成这一任务,
∴省略的部分是:实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务.
故选:A.
二.填空题(共6小题)
9.(2025 南京三模)使式子有意义的x的取值范围是 x≠1 .
【解答】解:根据题意得x﹣1≠0,
解得x≠1,
故答案为:x≠1.
10.(2025 福建模拟)已知非零实数a,b满足,且a≠b,则的值等于 2 .
【解答】解:∵非零实数a,b满足,且a≠b,
∴2,
∴a﹣2b=2ab,
原式
=2,
故答案为:2.
11.(2025 凉山州)若关于x的分式方程3无解,则m= ﹣1 .
【解答】解:原方程去分母:方程两边同时乘以x﹣2,得:
x+m﹣1=3x﹣6,
x﹣3x=﹣6﹣m+1,
﹣2x=﹣5﹣m,
,
∵原方程无解,
∴是原方程的增根,
由x﹣2=0,x=2,
∴,
∴m=﹣1,
故答案为:﹣1.
12.(2025春 温江区校级月考)已知:a+2b=2025,则分式 .
【解答】解:∵a+2b=2025,
∴,
故答案为:.
13.(2025春 南岸区期中)若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 2 .
【解答】解:∵,
解①得:y≤9;
解②得,
∴不等式组的解集为,
∵不等式组有且只有5个奇数解,
解得:﹣3≤m<5;
∵,
解得:,
∵方程有整数解,且x≠1,﹣3≤m<5,
∴m的值为﹣2,4,
∴﹣2+4=2,
故答案为:2.
14.(2025春 奉贤区月考)用换元法解分式方程,如果设y=x2﹣x,那么原方程可化为关于y的整式方程是 y2﹣y﹣6=0 .
【解答】解:设y=x2﹣x,
则方程变形为,
方程两边同时乘y,得y2﹣y=6,即y2﹣y﹣6=0.
故答案为:y2﹣y﹣6=0.
三.解答题(共6小题)
15.(2025 晋江市模拟)解分式方程:.
【解答】解:原方程可化为:﹣3+2(x﹣4)=1﹣x,解得x=4,
把x=4代入x﹣4得,4﹣4=0,
故x=4是原分式方程的增根,原方程无解.
16.(2025 昭通模拟)先化简,再求值(a+2),其中a=﹣2.
【解答】解:原式
,
当a=﹣2时,原式.
17.(2025 楚雄州模拟)本着低碳出行与强身健体的理念,赵老师决定改骑共享单车上下班.通过一段时间的体验,赵老师发现每天上班所用时间只比自驾车多0.3小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是骑共享单车速度的2倍,求赵老师骑共享单车每小时行驶多少千米.
【解答】解:设赵老师骑共享单车每小时行驶x千米,则自驾车每小时行驶2x千米,
根据题意得:,
解得x=20,
经检验 x=20 是所列方程的解,且符合题目要求,
∴x=20,
答:赵老师骑共享单车每小时行驶20千米.
18.(2025 怒江州模拟)云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
【解答】解:设实际每天采摘鲜叶x kg,则原计划每天采摘鲜叶(x﹣300)kg,
根据题意得,,
解得x=550,
经检验,x=550是分式方程的解,
答:实际每天采摘鲜叶550kg.
19.(2024秋 荣昌区期末)为激励同学们参与数学阅读,罗老师准备购买两种不同的笔记本奖励给部分同学.已知A种笔记本的单价比B种笔记本单价多2元,他花50元购买A种笔记本数量与花40元购买B种笔记本数量相同.
(1)A,B两种笔记本的单价各是多少元?
(2)罗老师在购买的时候,决定对全班50名同学进行奖励,每人奖一个笔记本,A种笔记本作为一等奖奖品,B种笔记本作为二等奖奖品,一等奖人数不少于二等奖人数的一半,罗老师所带现金共440元,在使用仅有现金的情况下,他购买A,B两种笔记本共有多少种可能的方案?请写出所有可能的购买方案.
【解答】解:(1)设A种笔记本的单价是a元,则B种笔记本的单价是(a﹣2)元,
根据题意得:,
解得:a=10,
经检验,a=10是原方程的解,且符合题意,
∴a﹣2=10﹣2=8,
答:A种笔记本的单价是10元,B种笔记本的单价是8元;
(2)设购买A种笔记本x本,则购买B种笔记本(50﹣x)本,
根据题意得不等式组:,
解不等式组得:16x≤20,
∵x为正整数,
∴x=17或18或19或20,
∴共有4种可能的方案:
①购买A种笔记本17本,B种笔记本33本;
②购买A种笔记本18本,B种笔记本32本;
③购买A种笔记本19本,B种笔记本31本;
④购买A种笔记本20本,B种笔记本30本.
20.(2025 广州二模)
背景 随着我国科技事业的不断发展,国产无人机越来越多应用于实际生活,为人们的生活带来了便利.
素材1
某农业公司预购进A,B两种型号的植保无人机用来喷洒农药,A型机比B型机平均每小时少喷洒2公顷农田,A型机喷洒40公顷农田所用时间与B型机喷洒50公顷农田所用时间相等.
素材2 若农业公司共购进20架无人机,A型无人机5万元/架,B型无人机6万元/架.
问题解决
任务1 A,B两种型号无人机平均每小时分别喷洒多少公顷地?
任务2 若公司要求这批无人机每小时至少喷洒180公顷农田,那么该公司如何购买A型和B型无人机,才能使总成本最低?并求出最低成本.
【解答】解:(1)设A种型号无人机平均每小时喷洒x公顷地,则B种型号无人机平均每小时喷洒(x+2)公顷地,
由题意得:,
解得:x=8,
经检验,x=8是原方程的解,且符合题意,
∴x+2=8+2=10,
答:A种型号无人机平均每小时喷洒8公顷地,B种型号无人机平均每小时喷洒10公顷地;
(2)设购买A型无人机m架,则购买B型无人机(20﹣m)架,
由题意得:8m+10(20﹣m)≥180,
解得:m≤10,
∵A型无人机5万元/架,B型无人机6万元/架,
∴m取最大值时,总成本最低,
∴m=10,
∴20﹣m=20﹣10=10,
最低成本为:10×5+10×6=110(万元),
答:购买A型无人机10架,购买B型无人机10架,才能使总成本最低,最低成本为110万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末章节复习】分式-2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2025 中山市三模)若分式的值等于0,则a的值为( )
A.±1 B.0 C.﹣1 D.1
2.(2024秋 长沙期末)把分式中的x,y的值都扩大为原来的3倍,则分式的值( )
A.缩小为原来的 B.不变
C.扩大为原来的6倍 D.扩大为原来的3倍
3.(2025春 小店区校级月考)下列各式中最简分式是( )
A. B.
C. D.
4.(2025春 郑州月考)若关于x的分式方程有增根,则a的值为( )
A.1 B.2 C.3 D.4
5.(2025春 万州区月考)如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A.扩大到原来的2倍 B.扩大到原来的4倍
C.不变 D.缩小到原来的
6.(2025 福田区校级三模)我国古代数学著作《九章算术》中有一道关于“驿站送信”的题目,其大意为:把一封信送到800里外的地方,若用慢马送,则晚1天送达;若用快马送则早3天送达,已知快马的速度是慢马速度的2倍,问规定的时间为多少天?快马的速度为多少?下列说法错误的是( )
A.设规定的时间为x天,所列方程为
B.规定的时间为7天
C.设慢马的速度为y里/天,所列方程为
D.快马速度是200里/天
7.(2025 福建模拟)随着无人机技术的发展,无人机表演越来越受欢迎.在一次无人机表演排练时,A无人机落后B无人机30米,已知B无人机的飞行速度为3米/秒,若A无人机飞行200米刚好追上B无人机,设A无人机接下来的飞行速度为x米/秒,则下列方程正确的是( )
A. B.
C. D.
8.(2025春 小店区校级月考)某地响应“绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”打造美好家园.某工程队承接了60万平方米的荒山绿化工程,由于情况有变…设原计划每天绿化的面积为x万平方米,列方程为.根据方程在题干中省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了25%,结果延误8天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了25%,结果延误8天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了25%,结果提前8天完成了这一任务
二.填空题(共6小题)
9.(2025 南京三模)使式子有意义的x的取值范围是 .
10.(2025 福建模拟)已知非零实数a,b满足,且a≠b,则的值等于 .
11.(2025 凉山州)若关于x的分式方程3无解,则m= .
12.(2025春 温江区校级月考)已知:a+2b=2025,则分式 .
13.(2025春 南岸区期中)若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 .
14.(2025春 奉贤区月考)用换元法解分式方程,如果设y=x2﹣x,那么原方程可化为关于y的整式方程是 .
三.解答题(共6小题)
15.(2025 晋江市模拟)解分式方程:.
16.(2025 昭通模拟)先化简,再求值(a+2),其中a=﹣2.
17.(2025 楚雄州模拟)本着低碳出行与强身健体的理念,赵老师决定改骑共享单车上下班.通过一段时间的体验,赵老师发现每天上班所用时间只比自驾车多0.3小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是骑共享单车速度的2倍,求赵老师骑共享单车每小时行驶多少千米.
18.(2025 怒江州模拟)云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
19.(2024秋 荣昌区期末)为激励同学们参与数学阅读,罗老师准备购买两种不同的笔记本奖励给部分同学.已知A种笔记本的单价比B种笔记本单价多2元,他花50元购买A种笔记本数量与花40元购买B种笔记本数量相同.
(1)A,B两种笔记本的单价各是多少元?
(2)罗老师在购买的时候,决定对全班50名同学进行奖励,每人奖一个笔记本,A种笔记本作为一等奖奖品,B种笔记本作为二等奖奖品,一等奖人数不少于二等奖人数的一半,罗老师所带现金共440元,在使用仅有现金的情况下,他购买A,B两种笔记本共有多少种可能的方案?请写出所有可能的购买方案.
20.(2025 广州二模)
背景 随着我国科技事业的不断发展,国产无人机越来越多应用于实际生活,为人们的生活带来了便利.
素材1
某农业公司预购进A,B两种型号的植保无人机用来喷洒农药,A型机比B型机平均每小时少喷洒2公顷农田,A型机喷洒40公顷农田所用时间与B型机喷洒50公顷农田所用时间相等.
素材2 若农业公司共购进20架无人机,A型无人机5万元/架,B型无人机6万元/架.
问题解决
任务1 A,B两种型号无人机平均每小时分别喷洒多少公顷地?
任务2 若公司要求这批无人机每小时至少喷洒180公顷农田,那么该公司如何购买A型和B型无人机,才能使总成本最低?并求出最低成本.
【期末章节复习】分式-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D B D C B C A A
一.选择题(共8小题)
1.(2025 中山市三模)若分式的值等于0,则a的值为( )
A.±1 B.0 C.﹣1 D.1
【解答】解:∵分式的值等于0,
∴a﹣1=0且a+1≠0,
解得:a=1.
故选:D.
2.(2024秋 长沙期末)把分式中的x,y的值都扩大为原来的3倍,则分式的值( )
A.缩小为原来的 B.不变
C.扩大为原来的6倍 D.扩大为原来的3倍
【解答】解:由题意得:,
∴把分式中的x,y的值都扩大为原来的3倍,则分式的值不变,
故选:B.
3.(2025春 小店区校级月考)下列各式中最简分式是( )
A. B.
C. D.
【解答】解:A. ,不是最简分式,故不符合题意;
B. ,不是最简分式,故不符合题意;
C. a+1,不是最简分式,故不符合题意;
D. 是最简分式,故符合题意;
故选:D.
4.(2025春 郑州月考)若关于x的分式方程有增根,则a的值为( )
A.1 B.2 C.3 D.4
【解答】解:两边都乘以x﹣2得,a+2(x﹣2)=x+1,
由于分式方程的增根为x=2,
当x=2时,即a+0=2+1,
即a=3.
故选:C.
5.(2025春 万州区月考)如果把分式中的x和y都扩大到原来的4倍,那么分式的值( )
A.扩大到原来的2倍 B.扩大到原来的4倍
C.不变 D.缩小到原来的
【解答】解:根据分式的基本性质可得:
,
∴如果把分式中的x和y都扩大为原来的4倍,那么分式的值扩大为原来的4倍,
故选:B.
6.(2025 福田区校级三模)我国古代数学著作《九章算术》中有一道关于“驿站送信”的题目,其大意为:把一封信送到800里外的地方,若用慢马送,则晚1天送达;若用快马送则早3天送达,已知快马的速度是慢马速度的2倍,问规定的时间为多少天?快马的速度为多少?下列说法错误的是( )
A.设规定的时间为x天,所列方程为
B.规定的时间为7天
C.设慢马的速度为y里/天,所列方程为
D.快马速度是200里/天
【解答】解:A、设规定时间为x天,则慢马用时(x+1)天,快马用时(x﹣3)天,
由题意得:,故选项A不符合题意;
解得:x=7,
经检验,x=7是原方程的解,且符合题意,故选项B不符合题意;
C、设慢马的速度为y里/天,则快马的速度为2y里/天,
由题意得:4,故选项C符合题意;
D、快马用了7﹣3=4天送达,速度为800÷4=200(里/天),故选项D不符合题意;
故选:C.
7.(2025 福建模拟)随着无人机技术的发展,无人机表演越来越受欢迎.在一次无人机表演排练时,A无人机落后B无人机30米,已知B无人机的飞行速度为3米/秒,若A无人机飞行200米刚好追上B无人机,设A无人机接下来的飞行速度为x米/秒,则下列方程正确的是( )
A. B.
C. D.
【解答】解:根据题意得:.
故选:A.
8.(2025春 小店区校级月考)某地响应“绿水青山变成金山银山,用绿色杠杆撬动经济转型”发展理念,开展“美化绿色城市”打造美好家园.某工程队承接了60万平方米的荒山绿化工程,由于情况有变…设原计划每天绿化的面积为x万平方米,列方程为.根据方程在题干中省略的部分是( )
A.实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务
B.实际工作时每天的工作效率比原计划提高了25%,结果延误8天完成了这一任务
C.实际工作时每天的工作效率比原计划降低了25%,结果延误8天完成了这一任务
D.实际工作时每天的工作效率比原计划降低了25%,结果提前8天完成了这一任务
【解答】解:方程为,
∴提高工作效率后比原计划提前8天完成这一任务,
∴省略的部分是:实际工作时每天的工作效率比原计划提高了25%,结果提前8天完成了这一任务.
故选:A.
二.填空题(共6小题)
9.(2025 南京三模)使式子有意义的x的取值范围是 x≠1 .
【解答】解:根据题意得x﹣1≠0,
解得x≠1,
故答案为:x≠1.
10.(2025 福建模拟)已知非零实数a,b满足,且a≠b,则的值等于 2 .
【解答】解:∵非零实数a,b满足,且a≠b,
∴2,
∴a﹣2b=2ab,
原式
=2,
故答案为:2.
11.(2025 凉山州)若关于x的分式方程3无解,则m= ﹣1 .
【解答】解:原方程去分母:方程两边同时乘以x﹣2,得:
x+m﹣1=3x﹣6,
x﹣3x=﹣6﹣m+1,
﹣2x=﹣5﹣m,
,
∵原方程无解,
∴是原方程的增根,
由x﹣2=0,x=2,
∴,
∴m=﹣1,
故答案为:﹣1.
12.(2025春 温江区校级月考)已知:a+2b=2025,则分式 .
【解答】解:∵a+2b=2025,
∴,
故答案为:.
13.(2025春 南岸区期中)若关于y的不等式组有且只有5个奇数解,且关于x的分式方程的解为整数,则符合条件的所有整数m的值的和为 2 .
【解答】解:∵,
解①得:y≤9;
解②得,
∴不等式组的解集为,
∵不等式组有且只有5个奇数解,
解得:﹣3≤m<5;
∵,
解得:,
∵方程有整数解,且x≠1,﹣3≤m<5,
∴m的值为﹣2,4,
∴﹣2+4=2,
故答案为:2.
14.(2025春 奉贤区月考)用换元法解分式方程,如果设y=x2﹣x,那么原方程可化为关于y的整式方程是 y2﹣y﹣6=0 .
【解答】解:设y=x2﹣x,
则方程变形为,
方程两边同时乘y,得y2﹣y=6,即y2﹣y﹣6=0.
故答案为:y2﹣y﹣6=0.
三.解答题(共6小题)
15.(2025 晋江市模拟)解分式方程:.
【解答】解:原方程可化为:﹣3+2(x﹣4)=1﹣x,解得x=4,
把x=4代入x﹣4得,4﹣4=0,
故x=4是原分式方程的增根,原方程无解.
16.(2025 昭通模拟)先化简,再求值(a+2),其中a=﹣2.
【解答】解:原式
,
当a=﹣2时,原式.
17.(2025 楚雄州模拟)本着低碳出行与强身健体的理念,赵老师决定改骑共享单车上下班.通过一段时间的体验,赵老师发现每天上班所用时间只比自驾车多0.3小时.已知赵老师家距学校12千米,上下班高峰时段,自驾车的速度是骑共享单车速度的2倍,求赵老师骑共享单车每小时行驶多少千米.
【解答】解:设赵老师骑共享单车每小时行驶x千米,则自驾车每小时行驶2x千米,
根据题意得:,
解得x=20,
经检验 x=20 是所列方程的解,且符合题目要求,
∴x=20,
答:赵老师骑共享单车每小时行驶20千米.
18.(2025 怒江州模拟)云南某茶园引入自动化采茶设备,原计划每天采摘固定数量的鲜叶,启用新设备后,实际每天采摘量比原计划多300kg.实际完成2200kg采摘任务所需时间与原计划完成1000kg采摘任务所需时间相等.求实际每天采摘鲜叶多少kg?
【解答】解:设实际每天采摘鲜叶x kg,则原计划每天采摘鲜叶(x﹣300)kg,
根据题意得,,
解得x=550,
经检验,x=550是分式方程的解,
答:实际每天采摘鲜叶550kg.
19.(2024秋 荣昌区期末)为激励同学们参与数学阅读,罗老师准备购买两种不同的笔记本奖励给部分同学.已知A种笔记本的单价比B种笔记本单价多2元,他花50元购买A种笔记本数量与花40元购买B种笔记本数量相同.
(1)A,B两种笔记本的单价各是多少元?
(2)罗老师在购买的时候,决定对全班50名同学进行奖励,每人奖一个笔记本,A种笔记本作为一等奖奖品,B种笔记本作为二等奖奖品,一等奖人数不少于二等奖人数的一半,罗老师所带现金共440元,在使用仅有现金的情况下,他购买A,B两种笔记本共有多少种可能的方案?请写出所有可能的购买方案.
【解答】解:(1)设A种笔记本的单价是a元,则B种笔记本的单价是(a﹣2)元,
根据题意得:,
解得:a=10,
经检验,a=10是原方程的解,且符合题意,
∴a﹣2=10﹣2=8,
答:A种笔记本的单价是10元,B种笔记本的单价是8元;
(2)设购买A种笔记本x本,则购买B种笔记本(50﹣x)本,
根据题意得不等式组:,
解不等式组得:16x≤20,
∵x为正整数,
∴x=17或18或19或20,
∴共有4种可能的方案:
①购买A种笔记本17本,B种笔记本33本;
②购买A种笔记本18本,B种笔记本32本;
③购买A种笔记本19本,B种笔记本31本;
④购买A种笔记本20本,B种笔记本30本.
20.(2025 广州二模)
背景 随着我国科技事业的不断发展,国产无人机越来越多应用于实际生活,为人们的生活带来了便利.
素材1
某农业公司预购进A,B两种型号的植保无人机用来喷洒农药,A型机比B型机平均每小时少喷洒2公顷农田,A型机喷洒40公顷农田所用时间与B型机喷洒50公顷农田所用时间相等.
素材2 若农业公司共购进20架无人机,A型无人机5万元/架,B型无人机6万元/架.
问题解决
任务1 A,B两种型号无人机平均每小时分别喷洒多少公顷地?
任务2 若公司要求这批无人机每小时至少喷洒180公顷农田,那么该公司如何购买A型和B型无人机,才能使总成本最低?并求出最低成本.
【解答】解:(1)设A种型号无人机平均每小时喷洒x公顷地,则B种型号无人机平均每小时喷洒(x+2)公顷地,
由题意得:,
解得:x=8,
经检验,x=8是原方程的解,且符合题意,
∴x+2=8+2=10,
答:A种型号无人机平均每小时喷洒8公顷地,B种型号无人机平均每小时喷洒10公顷地;
(2)设购买A型无人机m架,则购买B型无人机(20﹣m)架,
由题意得:8m+10(20﹣m)≥180,
解得:m≤10,
∵A型无人机5万元/架,B型无人机6万元/架,
∴m取最大值时,总成本最低,
∴m=10,
∴20﹣m=20﹣10=10,
最低成本为:10×5+10×6=110(万元),
答:购买A型无人机10架,购买B型无人机10架,才能使总成本最低,最低成本为110万元.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第7章 数据的收集、整理、描述
- 7.1 普查与抽样调查
- 7.2 统计图的选用
- 7.3 频数和频率
- 7.4 频数分布表和频数分布直方图
- 第8章 认识概率
- 8.1 确定事件与随机事件
- 8.2 可能性的大小
- 8.3 频率与概率
- 第9章 中心对称图形——平行四边形
- 9.1 图形的旋转
- 9.2 中心对称与中心对称图形
- 9.3 平行四边形
- 9.4 矩形、菱形、正方形
- 9.5 三角形的中位线
- 第10章 分式
- 10.1 分式
- 10.2 分式的基本性质
- 10.3 分式的加减
- 10.4 分式的乘除
- 10.5 分式方程
- 第11章 反比例函数
- 11.1 反比例函数
- 11.2 反比例函数的图象与性质
- 11.3 用反比例函数解决问题
- 第12章 二次根式
- 12.1 二次根式
- 12.2 二次根式的乘除
- 12.3 二次根式的加减
