【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 14:33:51 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2025 宿迁模拟)已知圆锥的轴截面为正三角形,外接球的半径为1,则圆锥的体积为( )
A. B. C. D.
2.(2025 湘潭模拟)现有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,则该平面在木料上的截面面积为( )
A. B. C. D.
3.(2025 山西模拟)已知球的半径和圆锥的底面半径相等,且圆锥的侧面展开图是圆心角为的扇形,则球与圆锥的体积之比为( )
A.2 B.3 C. D.
4.(2025 鹤壁二模)在直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,若该棱柱外接球的表面积为12π,则侧面BB1C1C绕直线BB1旋转一周所得到的旋转体的体积为( )
A.12π B.16π C.20π D.24π
5.(2025春 浙江月考)圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,则四边形ABDC的面积的最大值为( )
A.72 B.144 C.150 D.156
6.(2025春 德州月考)已知球O的表面积为16π,一正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,侧面与下底面所成角的余弦值为,则该棱台的体积为( )
A. B. C. D.
7.(2025春 龙岩期中)有一个底面直径为4的圆柱形容器(不考虑该容器的厚度),该圆柱形容器盛有部分水,且水面到容器口的距离为9.现将一个半径为R的小球放入该容器中,小球全部在水面下:且水没有溢出容器,则R的最大值是( )
A.2 B. C. D.3
8.(2025春 惠州月考)紫砂壶是中国特有的手工制造陶土工艺品.如图球形的壶体可以近似看成一个半径为6cm球体,那么该壶装满茶水后全部倒入底面半径为3cm且高为4cm的圆柱形茶杯内,则需要的茶杯个数最少为( )
A.6 B.7 C.8 D.9
二.多选题(共3小题)
(多选)9.(2025春 广东月考)已知圆锥的底面半径r=2,母线长l=6,设该圆锥的侧面展开图为扇形AOB,O为扇形圆心,则( )
A.扇形AOB的圆心角α为
B.圆锥的高h为
C.圆锥的表面积为16π
D.从A点绕圆锥侧面一周回到A点的最短距离为
(多选)10.(2025春 吴中区校级月考)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,则下列结论正确的是( )
A.圆锥SO的侧面积为2π
B.三棱锥S﹣ABC体积的最大值为
C.∠SAB的取值范围是
D.若AB=BC,E为线段AB上的动点,则SE+CE的最小值为
(多选)11.(2025春 渝中区校级期中)如图,ABCD是边长为2的正方形,AA1,BB1,CC1,DD1都垂直于底面ABCD,且,点E在线段CC1上,平面BED1交线段AA1于点F,则( )
A.A1,B1,C1,D1四点不共面
B.该几何体的体积为8
C.若BC中点为G,H为CC1的四等分点(靠近C1),则AG、DC、D1H三线共点
D.截面四边形BED1F的周长的最小值为10
三.填空题(共3小题)
12.(2025春 惠州月考)若圆锥的表面积为16π,且其母线长是底面半径的3倍,则圆锥的体积为 .
13.(2025春 浙江月考)已知三棱锥P﹣ABC的底面ABC是等腰直角三角形,∠ABC=90°,且AB=BC=4.,PB=PC,则当三棱锥体积最大时,其外接球的表面积为 .
14.(2025 宁远县模拟)三棱柱ABC﹣A1B1C1的体积为1,P点为四边形BB1C1C的中心,则四面体A1﹣B1PB的体积与三棱柱ABC﹣A1B1C1的体积比为 .
四.解答题(共5小题)
15.(2025春 广东月考)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=3,AC=4,BC=5.
(1)求证:AB⊥平面ACC1A1;
(2)若异面直线BB1与A1C所成的角为30°,求三棱柱ABC﹣A1B1C1的体积.
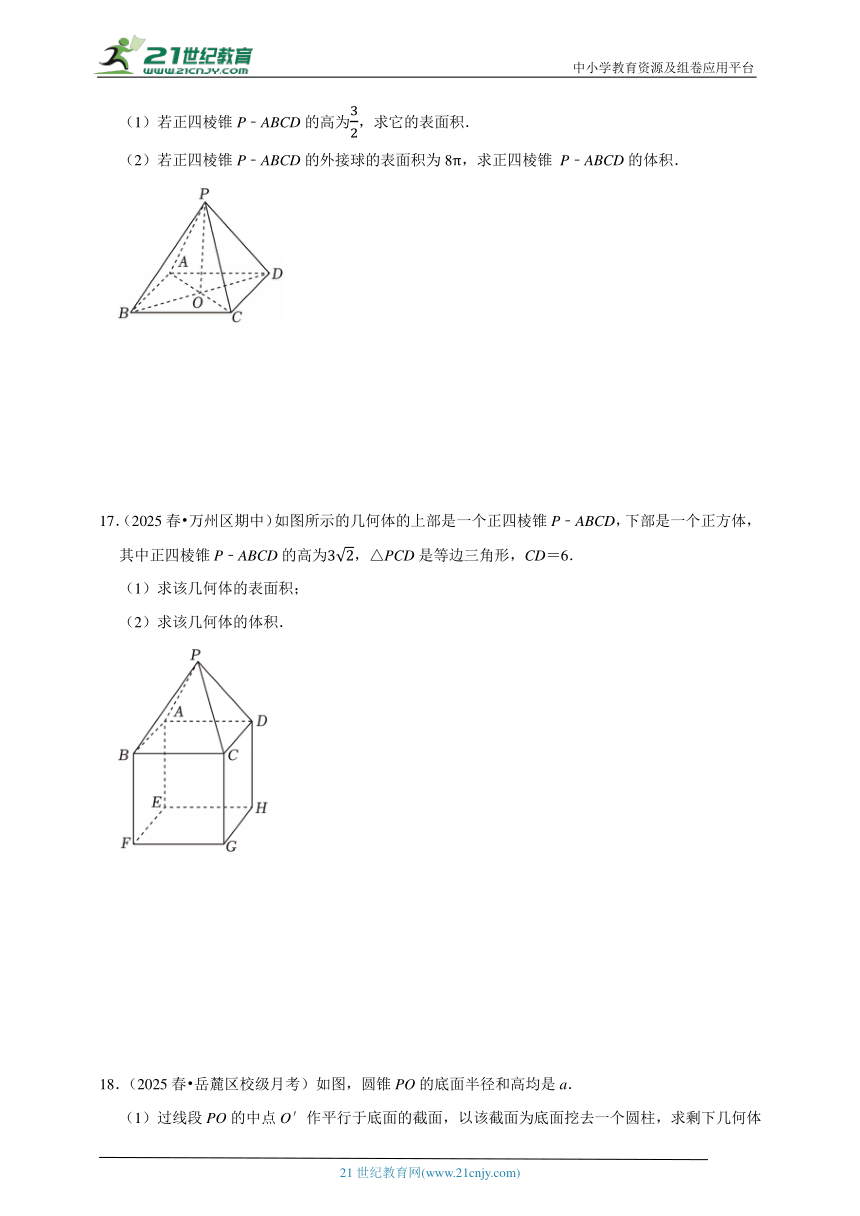
16.(2025春 浙江期中)如图,正四棱锥P﹣ABCD的底面积为3,O为正方形ABCD的中心.
(1)若正四棱锥P﹣ABCD的高为,求它的表面积.
(2)若正四棱锥P﹣ABCD的外接球的表面积为8π,求正四棱锥 P﹣ABCD的体积.
17.(2025春 万州区期中)如图所示的几何体的上部是一个正四棱锥P﹣ABCD,下部是一个正方体,其中正四棱锥P﹣ABCD的高为,△PCD是等边三角形,CD=6.
(1)求该几何体的表面积;
(2)求该几何体的体积.
18.(2025春 岳麓区校级月考)如图,圆锥PO的底面半径和高均是a.
(1)过线段PO的中点O′作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的体积.
(2)若过线段PO上的任意一点作平行于底面的截面,并以该截面为底面挖去一个圆柱,求剩下几何体的最大表面积.
19.(2025春 秀英区校级期中)刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),例如:正方体在每个顶点有3个面角,每个面角是,所以正方体在各顶点的曲率为,已知四棱锥P﹣ABCD在点A的曲率为,且PB=PD,CB=CD,.
(1)若点B的曲率为,∠PBC=∠ABC,求四棱锥P﹣ABCD的表面积;
(2)若点E在PD上,且PE:ED=2:1.试探究:在棱PC上是否存在点F,使BF∥平面AEC?证明你的结论.
【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A D C B C A A C
二.多选题(共3小题)
题号 9 10 11
答案 BCD BD BCD
一.选择题(共8小题)
1.(2025 宿迁模拟)已知圆锥的轴截面为正三角形,外接球的半径为1,则圆锥的体积为( )
A. B. C. D.
【解答】解:如图,
设圆锥的底面半径为r,由于圆锥轴截面为等边三角形,
可得圆锥的母线长为2r,圆锥外接球半径即为轴截面等边三角形的外接圆半径,
由正弦定理可得,则,
圆锥的高为,
故该圆锥的体积为.
故选:A.
2.(2025 湘潭模拟)现有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,则该平面在木料上的截面面积为( )
A. B. C. D.
【解答】解:已知有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,
由正四面体木料知,底面为边长为2的正三角形,故底面面积为,
因为平面平行于该木料底面,故该平面在木料上的截面也为正三角形,
设该正三角形与底面的相似比为k,则该平面在木料上的截面面积为,
截下部分一部分为小四面体,一部分为正三棱台,其中小四面体部分的表面积即,
正三棱台表面积为,
故,解得,所以该平面在木料上的截面面积为.
故选:D.
3.(2025 山西模拟)已知球的半径和圆锥的底面半径相等,且圆锥的侧面展开图是圆心角为的扇形,则球与圆锥的体积之比为( )
A.2 B.3 C. D.
【解答】解:因为球的半径和圆锥的底面半径相等,
设球的半径和圆锥的底面半径均为r,圆锥的母线长为l,
由圆锥的侧面展开图是圆心角为的扇形,
得,则l=3r,
所以球的体积与圆锥的体积之比为.
故选:C.
4.(2025 鹤壁二模)在直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,若该棱柱外接球的表面积为12π,则侧面BB1C1C绕直线BB1旋转一周所得到的旋转体的体积为( )
A.12π B.16π C.20π D.24π
【解答】解:由题意直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,
该棱柱外接球的表面积为12π,
可知三棱柱两个底面三角形的外接圆的圆心分别为B1C1,BC的中点,.
设外接球的半径为R,则,
所以,解得CC1=2.
侧面BB1C1C旋转后得到的几何体是底面半径为,高为2的圆柱,
其体积为.
故选:B.
5.(2025春 浙江月考)圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,则四边形ABDC的面积的最大值为( )
A.72 B.144 C.150 D.156
【解答】解:因为圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,
如图,延长BA、DC交于点P,将圆台补成的圆锥的母线长为l,
所以,解得l=20,
所以,故,
设轴截面的顶角为θ,则,
所以θ为钝角,所以0<∠BPD≤θ,
所以当PB⊥PD时,S△PBD取最大值,且其最大值为,
所以梯形ABDC面积的最大值为.
故选:C.
6.(2025春 德州月考)已知球O的表面积为16π,一正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,侧面与下底面所成角的余弦值为,则该棱台的体积为( )
A. B. C. D.
【解答】解:设球O的半径为R,
所以球O的表面积为4πR2=16π,
所以,
又正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,
所以下底面边长为,
设棱台的上底面边长为,高为h,
则,解得,
所以该棱台的体积为.
故选:A.
7.(2025春 龙岩期中)有一个底面直径为4的圆柱形容器(不考虑该容器的厚度),该圆柱形容器盛有部分水,且水面到容器口的距离为9.现将一个半径为R的小球放入该容器中,小球全部在水面下:且水没有溢出容器,则R的最大值是( )
A.2 B. C. D.3
【解答】解:设圆柱的高为h,则h>9,设R的最大值是r,r<2,
所以根据题意可得,
解得r=3>2,所以r只能取2.
故选:A.
8.(2025春 惠州月考)紫砂壶是中国特有的手工制造陶土工艺品.如图球形的壶体可以近似看成一个半径为6cm球体,那么该壶装满茶水后全部倒入底面半径为3cm且高为4cm的圆柱形茶杯内,则需要的茶杯个数最少为( )
A.6 B.7 C.8 D.9
【解答】解:设需要的茶杯个数为a,
则根据题意可得aπ×32×4,
解得a≥8.
故选:C.
二.多选题(共3小题)
(多选)9.(2025春 广东月考)已知圆锥的底面半径r=2,母线长l=6,设该圆锥的侧面展开图为扇形AOB,O为扇形圆心,则( )
A.扇形AOB的圆心角α为
B.圆锥的高h为
C.圆锥的表面积为16π
D.从A点绕圆锥侧面一周回到A点的最短距离为
【解答】解:A,根据题意可知,圆锥的底面半径r=2,母线长l=6,
设圆锥的侧面展开图所得扇形的圆心角为α,可得θ×l=2πr,
即6α=2π×2=4π,解得,所以A错误;
B,圆锥的高为,所以B正确;
C,由圆锥的侧面积为S1=πrl=π×2×6=12π,底面积为,
所以圆锥的表面积为S=S1+S2=16π,所以C正确;
D,如图所示,圆锥的侧面展开图中,可得,
即从A点绕圆锥侧面一周回到A点的最短距离为,所以D正确.
故选:BCD.
(多选)10.(2025春 吴中区校级月考)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,则下列结论正确的是( )
A.圆锥SO的侧面积为2π
B.三棱锥S﹣ABC体积的最大值为
C.∠SAB的取值范围是
D.若AB=BC,E为线段AB上的动点,则SE+CE的最小值为
【解答】解:因为AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,
所以,半径r=OC=1.
对于选项A:圆锥SO的侧面积为,故选项A错误;
对于选项B:由圆的几何性质可知AB⊥BC,由勾股定理可得AB2+BC2=AC2=4,
所以4=AB2+BC2≥2AB BC,可得AB BC≤2,
即,当且仅当时,等号成立,
则三棱锥S﹣ABC体积为,故选项B正确;
对于选项C:因为SA2+SC2=2+2=4=AC2,故,
当点B与点A重合时,∠ASB=0;当点B与点C重合时,,
又因为点B与A、C不重合,则,
又2∠SAB+∠ASB=π,可得,故选项C错误;
对于选项D:因为AB=BC,,AC=2,可得.
又,所以△SAB为等边三角形,则.
将△SAB以AB为轴旋转到与△ABC共面,
得到△S1AB,则△S1AB为等边三角形,.
如图,当S1、E、C三点共线时,SE+CE取最小值S1C.
因为,,
所以,
,故选项D正确.
故选:BD.
(多选)11.(2025春 渝中区校级期中)如图,ABCD是边长为2的正方形,AA1,BB1,CC1,DD1都垂直于底面ABCD,且,点E在线段CC1上,平面BED1交线段AA1于点F,则( )
A.A1,B1,C1,D1四点不共面
B.该几何体的体积为8
C.若BC中点为G,H为CC1的四等分点(靠近C1),则AG、DC、D1H三线共点
D.截面四边形BED1F的周长的最小值为10
【解答】解:对于选项A,取AA1中点M,取DD1靠近D1的三等分点N,
则四边形NMA1D1为平行四边形,四边形NMB1C1为平行四边形,
∴MN∥A1D1,MN∥B1C1,则B1C1∥A1D1,
∴A1,B1,C1,D1四点共面,故A选项错误;
对于选项B,由对称性知,此几何体体积是底面边长为2的正方形,高为4的长方体体积的一半,
∴该几何体的体积为,故B选项正确;
对于选项C,若BC中点为G,H为CC1的四等分点(靠近C1),
由已知CC1=2,则,
延长AG、DC,设它们交于点M,则△ABG~△MCG,
又AB=2,∴MG=2,
延长D1H、DC,设它们交于点N,则△D1DN~△HCN,
则,即,
又DD1=3,CC1=2,则,则CN=2,
∴点M与点N重合,即AG、DC、D1H三线共点,故C选项正确.
对于选项D,由题意,平面ADD1A1∥平面BCB1C1,
平面ADD1A1∩平面BED1=D1F,平面BCB1C1∩平面BED1=BE,
∴D1F∥BE,同理可得BF∥D1E,
∴四边形BED1F为平行四边形,则周长l=2(BE+ED1),
沿CC1将右面和后面相邻两面展开,
当B,E,D1三点共线时,BE+ED1最小,最小值为,
∴截面四边形BED1F的周长的最小值为10,故D选项正确.
故选:BCD.
三.填空题(共3小题)
12.(2025春 惠州月考)若圆锥的表面积为16π,且其母线长是底面半径的3倍,则圆锥的体积为 .
【解答】解:设圆锥底面半径为r,母线长为l,高为h,
则l=3r,πrl+πr2=16π,解得r=2,l=6,h4,
所以圆锥的体积为.
故答案为:.
13.(2025春 浙江月考)已知三棱锥P﹣ABC的底面ABC是等腰直角三角形,∠ABC=90°,且AB=BC=4.,PB=PC,则当三棱锥体积最大时,其外接球的表面积为 32π .
【解答】解:因为三棱锥P﹣ABC的底面ABC是等腰直角三角形,且∠ABC=90°,
又AB=BC=4.,PB=PC,
所以P在BC的中垂面上,
所以P的轨迹为BC中垂面与以A为球心,为半径的球的交线,
即P的轨迹为如图以D为圆心,2为半径的圆,且O是BC的中点,如图所示,
因为∠ABC=90°,AB=BC=4,所以由勾股定理得,
由三角形面积公式得,
若三棱锥体积最大,则P到面ABC的距离最大即可,此时P在最上面,
易得PD=2,AB=BC=DO=4,CO=2,
且由勾股定理得,此时,
则PC2+PA2=32=AC2,即AP⊥PC,
得到外接球球心为AC的中点,即球的半径为,
由球的表面积公式得球的表面积为.
故答案为:32π.
14.(2025 宁远县模拟)三棱柱ABC﹣A1B1C1的体积为1,P点为四边形BB1C1C的中心,则四面体A1﹣B1PB的体积与三棱柱ABC﹣A1B1C1的体积比为 .
【解答】解:如图,在三棱柱ABC﹣A1B1C1中,,
而四面体A1﹣ABC的体积,
所以.
故答案为:.
四.解答题(共5小题)
15.(2025春 广东月考)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=3,AC=4,BC=5.
(1)求证:AB⊥平面ACC1A1;
(2)若异面直线BB1与A1C所成的角为30°,求三棱柱ABC﹣A1B1C1的体积.
【解答】解:(1)证明:因为AA1⊥平面ABC,AB 平面ABC,
所以AA1⊥AB,
又AB=3,AC=4,BC=5,所以AB2+AC2=BC2,所以AC⊥AB.
又AA1∩AC=A,AA1,AC 平面ACC1A1,
所以AB⊥平面ACC1A1;
(2)因为BB1∥AA1,
所以异面直线BB1与A1C所成的角为∠AA1C=30°,
又AA1⊥平面ABC,AC 平面ABC,
所以AA1⊥AC,所以可得,,
所以三棱柱ABC﹣A1B1C1的体积.
16.(2025春 浙江期中)如图,正四棱锥P﹣ABCD的底面积为3,O为正方形ABCD的中心.
(1)若正四棱锥P﹣ABCD的高为,求它的表面积.
(2)若正四棱锥P﹣ABCD的外接球的表面积为8π,求正四棱锥 P﹣ABCD的体积.
【解答】解:(1)因为正四棱锥P﹣ABCD的底面积为3,
所以底面正方形的边长为,
若正四棱锥P﹣ABCD的高为,
则其斜高为,
所以该正四棱锥的表面积为9;
(2)设正四棱锥P﹣ABCD的外接球的半径为R,
若正四棱锥P﹣ABCD的外接球的表面积为8π,
则4πR2=8π,所以R,
又正方形ABCD的中心O到正方形顶点的距离为,
所以根据勾股定理可得:
球心到底面的距离为,
所以正四棱锥P﹣ABCD的高为或,
所以正四棱锥 P﹣ABCD的体积为或.
17.(2025春 万州区期中)如图所示的几何体的上部是一个正四棱锥P﹣ABCD,下部是一个正方体,其中正四棱锥P﹣ABCD的高为,△PCD是等边三角形,CD=6.
(1)求该几何体的表面积;
(2)求该几何体的体积.
【解答】解:(1)设M是CD的中点,连接PM,
因为△PCD是边长为6的正三角形,
所以PM⊥CD,且,
所以该几何体的表面积;
(2)连接AC,BD,设交点为O,连接PO,则PO是四棱锥 P﹣ABCD的高,
则,
所以,
又正方体的体积为6×6×6=216,
所以该几何体的体积.
18.(2025春 岳麓区校级月考)如图,圆锥PO的底面半径和高均是a.
(1)过线段PO的中点O′作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的体积.
(2)若过线段PO上的任意一点作平行于底面的截面,并以该截面为底面挖去一个圆柱,求剩下几何体的最大表面积.
【解答】解:(1)如图,设圆锥母线PB与圆柱交点为A,连接O′A,则PO=OB=a,
因为O′为PO中点,
所以圆柱的高OO'POa,圆柱的底面半径O′Aa,
因为圆锥内部挖去一个圆柱,
所以剩下几何体的体积Vππa3.
(2)因为圆锥PO的底面半径和高均是a,
所以圆锥的母线长为,
所以圆锥的表面积S1,
设圆柱的半径为r,高为h,
由题意知,,即,
解得h=a﹣r,
所以圆柱的侧面积S2=2πr h=2πr(a﹣r),
所以剩下几何体的表面积S=S1+S22πr(a﹣r)2π πa2=()πa2,
当且仅当r=a﹣r,即r时,等号成立,
故剩下几何体的最大表面积为()πa2.
19.(2025春 秀英区校级期中)刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),例如:正方体在每个顶点有3个面角,每个面角是,所以正方体在各顶点的曲率为,已知四棱锥P﹣ABCD在点A的曲率为,且PB=PD,CB=CD,.
(1)若点B的曲率为,∠PBC=∠ABC,求四棱锥P﹣ABCD的表面积;
(2)若点E在PD上,且PE:ED=2:1.试探究:在棱PC上是否存在点F,使BF∥平面AEC?证明你的结论.
【解答】解:(1)
由,
利用余弦定理可得:,
由∠BAD∈(0,π)可得:,利用内角和定理可得,
此时,
又因为PB=PD,PA=AB=AD,所以△PAD≌△PAB,即∠PAD=∠PAB,
根据四棱锥P﹣ABCD在点A的曲率为,
可得,
利用内角和定理可得,此时
再由点B的曲率为,∠PBC=∠ABC,可得,
因为,所以,又因为CB=CD,所以三角形CBD是等边三角形,
此时,由于,
所以,利用△PBC≌△PDC,
可知,
所以四棱锥P﹣ABCD的表面积为;
(2)证明:
取M,F分别为PE,PC的中点,AC∩BD=O,连接OE,BM,MF,BF,
利用中位线可知MF∥CE,又由CB=CD,AB=AD,可得△ABC≌△ADC,
即∠BAC=∠DAC,又可证得△ABO≌△ADO,即BO=OD,又因为E为MD中点,
所以OE∥BM,又因为OE 平面AEC,BMd平面AEC,
所以BM∥平面AEC,同理由MF∥CE,可证明MF∥平面AEC,
又因为BM∩MF=M,BM,MF 平面BMF,所以平面BMF∥平面AEC,
又因为BF 平面BMF,所以BF∥平面AEC,此时F为PC的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2025 宿迁模拟)已知圆锥的轴截面为正三角形,外接球的半径为1,则圆锥的体积为( )
A. B. C. D.
2.(2025 湘潭模拟)现有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,则该平面在木料上的截面面积为( )
A. B. C. D.
3.(2025 山西模拟)已知球的半径和圆锥的底面半径相等,且圆锥的侧面展开图是圆心角为的扇形,则球与圆锥的体积之比为( )
A.2 B.3 C. D.
4.(2025 鹤壁二模)在直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,若该棱柱外接球的表面积为12π,则侧面BB1C1C绕直线BB1旋转一周所得到的旋转体的体积为( )
A.12π B.16π C.20π D.24π
5.(2025春 浙江月考)圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,则四边形ABDC的面积的最大值为( )
A.72 B.144 C.150 D.156
6.(2025春 德州月考)已知球O的表面积为16π,一正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,侧面与下底面所成角的余弦值为,则该棱台的体积为( )
A. B. C. D.
7.(2025春 龙岩期中)有一个底面直径为4的圆柱形容器(不考虑该容器的厚度),该圆柱形容器盛有部分水,且水面到容器口的距离为9.现将一个半径为R的小球放入该容器中,小球全部在水面下:且水没有溢出容器,则R的最大值是( )
A.2 B. C. D.3
8.(2025春 惠州月考)紫砂壶是中国特有的手工制造陶土工艺品.如图球形的壶体可以近似看成一个半径为6cm球体,那么该壶装满茶水后全部倒入底面半径为3cm且高为4cm的圆柱形茶杯内,则需要的茶杯个数最少为( )
A.6 B.7 C.8 D.9
二.多选题(共3小题)
(多选)9.(2025春 广东月考)已知圆锥的底面半径r=2,母线长l=6,设该圆锥的侧面展开图为扇形AOB,O为扇形圆心,则( )
A.扇形AOB的圆心角α为
B.圆锥的高h为
C.圆锥的表面积为16π
D.从A点绕圆锥侧面一周回到A点的最短距离为
(多选)10.(2025春 吴中区校级月考)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,则下列结论正确的是( )
A.圆锥SO的侧面积为2π
B.三棱锥S﹣ABC体积的最大值为
C.∠SAB的取值范围是
D.若AB=BC,E为线段AB上的动点,则SE+CE的最小值为
(多选)11.(2025春 渝中区校级期中)如图,ABCD是边长为2的正方形,AA1,BB1,CC1,DD1都垂直于底面ABCD,且,点E在线段CC1上,平面BED1交线段AA1于点F,则( )
A.A1,B1,C1,D1四点不共面
B.该几何体的体积为8
C.若BC中点为G,H为CC1的四等分点(靠近C1),则AG、DC、D1H三线共点
D.截面四边形BED1F的周长的最小值为10
三.填空题(共3小题)
12.(2025春 惠州月考)若圆锥的表面积为16π,且其母线长是底面半径的3倍,则圆锥的体积为 .
13.(2025春 浙江月考)已知三棱锥P﹣ABC的底面ABC是等腰直角三角形,∠ABC=90°,且AB=BC=4.,PB=PC,则当三棱锥体积最大时,其外接球的表面积为 .
14.(2025 宁远县模拟)三棱柱ABC﹣A1B1C1的体积为1,P点为四边形BB1C1C的中心,则四面体A1﹣B1PB的体积与三棱柱ABC﹣A1B1C1的体积比为 .
四.解答题(共5小题)
15.(2025春 广东月考)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=3,AC=4,BC=5.
(1)求证:AB⊥平面ACC1A1;
(2)若异面直线BB1与A1C所成的角为30°,求三棱柱ABC﹣A1B1C1的体积.
16.(2025春 浙江期中)如图,正四棱锥P﹣ABCD的底面积为3,O为正方形ABCD的中心.
(1)若正四棱锥P﹣ABCD的高为,求它的表面积.
(2)若正四棱锥P﹣ABCD的外接球的表面积为8π,求正四棱锥 P﹣ABCD的体积.
17.(2025春 万州区期中)如图所示的几何体的上部是一个正四棱锥P﹣ABCD,下部是一个正方体,其中正四棱锥P﹣ABCD的高为,△PCD是等边三角形,CD=6.
(1)求该几何体的表面积;
(2)求该几何体的体积.
18.(2025春 岳麓区校级月考)如图,圆锥PO的底面半径和高均是a.
(1)过线段PO的中点O′作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的体积.
(2)若过线段PO上的任意一点作平行于底面的截面,并以该截面为底面挖去一个圆柱,求剩下几何体的最大表面积.
19.(2025春 秀英区校级期中)刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),例如:正方体在每个顶点有3个面角,每个面角是,所以正方体在各顶点的曲率为,已知四棱锥P﹣ABCD在点A的曲率为,且PB=PD,CB=CD,.
(1)若点B的曲率为,∠PBC=∠ABC,求四棱锥P﹣ABCD的表面积;
(2)若点E在PD上,且PE:ED=2:1.试探究:在棱PC上是否存在点F,使BF∥平面AEC?证明你的结论.
【期末重点专题】简单几何体的表面积与体积-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A D C B C A A C
二.多选题(共3小题)
题号 9 10 11
答案 BCD BD BCD
一.选择题(共8小题)
1.(2025 宿迁模拟)已知圆锥的轴截面为正三角形,外接球的半径为1,则圆锥的体积为( )
A. B. C. D.
【解答】解:如图,
设圆锥的底面半径为r,由于圆锥轴截面为等边三角形,
可得圆锥的母线长为2r,圆锥外接球半径即为轴截面等边三角形的外接圆半径,
由正弦定理可得,则,
圆锥的高为,
故该圆锥的体积为.
故选:A.
2.(2025 湘潭模拟)现有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,则该平面在木料上的截面面积为( )
A. B. C. D.
【解答】解:已知有一块棱长为2的正四面体木料,用平行于该木料底面的一个平面将木料截成两部分,若这两部分的表面积相等,
由正四面体木料知,底面为边长为2的正三角形,故底面面积为,
因为平面平行于该木料底面,故该平面在木料上的截面也为正三角形,
设该正三角形与底面的相似比为k,则该平面在木料上的截面面积为,
截下部分一部分为小四面体,一部分为正三棱台,其中小四面体部分的表面积即,
正三棱台表面积为,
故,解得,所以该平面在木料上的截面面积为.
故选:D.
3.(2025 山西模拟)已知球的半径和圆锥的底面半径相等,且圆锥的侧面展开图是圆心角为的扇形,则球与圆锥的体积之比为( )
A.2 B.3 C. D.
【解答】解:因为球的半径和圆锥的底面半径相等,
设球的半径和圆锥的底面半径均为r,圆锥的母线长为l,
由圆锥的侧面展开图是圆心角为的扇形,
得,则l=3r,
所以球的体积与圆锥的体积之比为.
故选:C.
4.(2025 鹤壁二模)在直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,若该棱柱外接球的表面积为12π,则侧面BB1C1C绕直线BB1旋转一周所得到的旋转体的体积为( )
A.12π B.16π C.20π D.24π
【解答】解:由题意直三棱柱ABC﹣A1B1C1中,AB=AC=2,AB⊥AC,
该棱柱外接球的表面积为12π,
可知三棱柱两个底面三角形的外接圆的圆心分别为B1C1,BC的中点,.
设外接球的半径为R,则,
所以,解得CC1=2.
侧面BB1C1C旋转后得到的几何体是底面半径为,高为2的圆柱,
其体积为.
故选:B.
5.(2025春 浙江月考)圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,则四边形ABDC的面积的最大值为( )
A.72 B.144 C.150 D.156
【解答】解:因为圆台的上下底面半径分别为8、16,AB、CD为圆台的两条母线,且AB=10,
如图,延长BA、DC交于点P,将圆台补成的圆锥的母线长为l,
所以,解得l=20,
所以,故,
设轴截面的顶角为θ,则,
所以θ为钝角,所以0<∠BPD≤θ,
所以当PB⊥PD时,S△PBD取最大值,且其最大值为,
所以梯形ABDC面积的最大值为.
故选:C.
6.(2025春 德州月考)已知球O的表面积为16π,一正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,侧面与下底面所成角的余弦值为,则该棱台的体积为( )
A. B. C. D.
【解答】解:设球O的半径为R,
所以球O的表面积为4πR2=16π,
所以,
又正四棱台的上、下底面顶点都在球O的球面上,且下底面过球心O,
所以下底面边长为,
设棱台的上底面边长为,高为h,
则,解得,
所以该棱台的体积为.
故选:A.
7.(2025春 龙岩期中)有一个底面直径为4的圆柱形容器(不考虑该容器的厚度),该圆柱形容器盛有部分水,且水面到容器口的距离为9.现将一个半径为R的小球放入该容器中,小球全部在水面下:且水没有溢出容器,则R的最大值是( )
A.2 B. C. D.3
【解答】解:设圆柱的高为h,则h>9,设R的最大值是r,r<2,
所以根据题意可得,
解得r=3>2,所以r只能取2.
故选:A.
8.(2025春 惠州月考)紫砂壶是中国特有的手工制造陶土工艺品.如图球形的壶体可以近似看成一个半径为6cm球体,那么该壶装满茶水后全部倒入底面半径为3cm且高为4cm的圆柱形茶杯内,则需要的茶杯个数最少为( )
A.6 B.7 C.8 D.9
【解答】解:设需要的茶杯个数为a,
则根据题意可得aπ×32×4,
解得a≥8.
故选:C.
二.多选题(共3小题)
(多选)9.(2025春 广东月考)已知圆锥的底面半径r=2,母线长l=6,设该圆锥的侧面展开图为扇形AOB,O为扇形圆心,则( )
A.扇形AOB的圆心角α为
B.圆锥的高h为
C.圆锥的表面积为16π
D.从A点绕圆锥侧面一周回到A点的最短距离为
【解答】解:A,根据题意可知,圆锥的底面半径r=2,母线长l=6,
设圆锥的侧面展开图所得扇形的圆心角为α,可得θ×l=2πr,
即6α=2π×2=4π,解得,所以A错误;
B,圆锥的高为,所以B正确;
C,由圆锥的侧面积为S1=πrl=π×2×6=12π,底面积为,
所以圆锥的表面积为S=S1+S2=16π,所以C正确;
D,如图所示,圆锥的侧面展开图中,可得,
即从A点绕圆锥侧面一周回到A点的最短距离为,所以D正确.
故选:BCD.
(多选)10.(2025春 吴中区校级月考)如图,AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,则下列结论正确的是( )
A.圆锥SO的侧面积为2π
B.三棱锥S﹣ABC体积的最大值为
C.∠SAB的取值范围是
D.若AB=BC,E为线段AB上的动点,则SE+CE的最小值为
【解答】解:因为AC为圆锥SO底面圆O的直径,点B是圆O上异于A、C的动点,SO=OC=1,
所以,半径r=OC=1.
对于选项A:圆锥SO的侧面积为,故选项A错误;
对于选项B:由圆的几何性质可知AB⊥BC,由勾股定理可得AB2+BC2=AC2=4,
所以4=AB2+BC2≥2AB BC,可得AB BC≤2,
即,当且仅当时,等号成立,
则三棱锥S﹣ABC体积为,故选项B正确;
对于选项C:因为SA2+SC2=2+2=4=AC2,故,
当点B与点A重合时,∠ASB=0;当点B与点C重合时,,
又因为点B与A、C不重合,则,
又2∠SAB+∠ASB=π,可得,故选项C错误;
对于选项D:因为AB=BC,,AC=2,可得.
又,所以△SAB为等边三角形,则.
将△SAB以AB为轴旋转到与△ABC共面,
得到△S1AB,则△S1AB为等边三角形,.
如图,当S1、E、C三点共线时,SE+CE取最小值S1C.
因为,,
所以,
,故选项D正确.
故选:BD.
(多选)11.(2025春 渝中区校级期中)如图,ABCD是边长为2的正方形,AA1,BB1,CC1,DD1都垂直于底面ABCD,且,点E在线段CC1上,平面BED1交线段AA1于点F,则( )
A.A1,B1,C1,D1四点不共面
B.该几何体的体积为8
C.若BC中点为G,H为CC1的四等分点(靠近C1),则AG、DC、D1H三线共点
D.截面四边形BED1F的周长的最小值为10
【解答】解:对于选项A,取AA1中点M,取DD1靠近D1的三等分点N,
则四边形NMA1D1为平行四边形,四边形NMB1C1为平行四边形,
∴MN∥A1D1,MN∥B1C1,则B1C1∥A1D1,
∴A1,B1,C1,D1四点共面,故A选项错误;
对于选项B,由对称性知,此几何体体积是底面边长为2的正方形,高为4的长方体体积的一半,
∴该几何体的体积为,故B选项正确;
对于选项C,若BC中点为G,H为CC1的四等分点(靠近C1),
由已知CC1=2,则,
延长AG、DC,设它们交于点M,则△ABG~△MCG,
又AB=2,∴MG=2,
延长D1H、DC,设它们交于点N,则△D1DN~△HCN,
则,即,
又DD1=3,CC1=2,则,则CN=2,
∴点M与点N重合,即AG、DC、D1H三线共点,故C选项正确.
对于选项D,由题意,平面ADD1A1∥平面BCB1C1,
平面ADD1A1∩平面BED1=D1F,平面BCB1C1∩平面BED1=BE,
∴D1F∥BE,同理可得BF∥D1E,
∴四边形BED1F为平行四边形,则周长l=2(BE+ED1),
沿CC1将右面和后面相邻两面展开,
当B,E,D1三点共线时,BE+ED1最小,最小值为,
∴截面四边形BED1F的周长的最小值为10,故D选项正确.
故选:BCD.
三.填空题(共3小题)
12.(2025春 惠州月考)若圆锥的表面积为16π,且其母线长是底面半径的3倍,则圆锥的体积为 .
【解答】解:设圆锥底面半径为r,母线长为l,高为h,
则l=3r,πrl+πr2=16π,解得r=2,l=6,h4,
所以圆锥的体积为.
故答案为:.
13.(2025春 浙江月考)已知三棱锥P﹣ABC的底面ABC是等腰直角三角形,∠ABC=90°,且AB=BC=4.,PB=PC,则当三棱锥体积最大时,其外接球的表面积为 32π .
【解答】解:因为三棱锥P﹣ABC的底面ABC是等腰直角三角形,且∠ABC=90°,
又AB=BC=4.,PB=PC,
所以P在BC的中垂面上,
所以P的轨迹为BC中垂面与以A为球心,为半径的球的交线,
即P的轨迹为如图以D为圆心,2为半径的圆,且O是BC的中点,如图所示,
因为∠ABC=90°,AB=BC=4,所以由勾股定理得,
由三角形面积公式得,
若三棱锥体积最大,则P到面ABC的距离最大即可,此时P在最上面,
易得PD=2,AB=BC=DO=4,CO=2,
且由勾股定理得,此时,
则PC2+PA2=32=AC2,即AP⊥PC,
得到外接球球心为AC的中点,即球的半径为,
由球的表面积公式得球的表面积为.
故答案为:32π.
14.(2025 宁远县模拟)三棱柱ABC﹣A1B1C1的体积为1,P点为四边形BB1C1C的中心,则四面体A1﹣B1PB的体积与三棱柱ABC﹣A1B1C1的体积比为 .
【解答】解:如图,在三棱柱ABC﹣A1B1C1中,,
而四面体A1﹣ABC的体积,
所以.
故答案为:.
四.解答题(共5小题)
15.(2025春 广东月考)如图,三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,AB=3,AC=4,BC=5.
(1)求证:AB⊥平面ACC1A1;
(2)若异面直线BB1与A1C所成的角为30°,求三棱柱ABC﹣A1B1C1的体积.
【解答】解:(1)证明:因为AA1⊥平面ABC,AB 平面ABC,
所以AA1⊥AB,
又AB=3,AC=4,BC=5,所以AB2+AC2=BC2,所以AC⊥AB.
又AA1∩AC=A,AA1,AC 平面ACC1A1,
所以AB⊥平面ACC1A1;
(2)因为BB1∥AA1,
所以异面直线BB1与A1C所成的角为∠AA1C=30°,
又AA1⊥平面ABC,AC 平面ABC,
所以AA1⊥AC,所以可得,,
所以三棱柱ABC﹣A1B1C1的体积.
16.(2025春 浙江期中)如图,正四棱锥P﹣ABCD的底面积为3,O为正方形ABCD的中心.
(1)若正四棱锥P﹣ABCD的高为,求它的表面积.
(2)若正四棱锥P﹣ABCD的外接球的表面积为8π,求正四棱锥 P﹣ABCD的体积.
【解答】解:(1)因为正四棱锥P﹣ABCD的底面积为3,
所以底面正方形的边长为,
若正四棱锥P﹣ABCD的高为,
则其斜高为,
所以该正四棱锥的表面积为9;
(2)设正四棱锥P﹣ABCD的外接球的半径为R,
若正四棱锥P﹣ABCD的外接球的表面积为8π,
则4πR2=8π,所以R,
又正方形ABCD的中心O到正方形顶点的距离为,
所以根据勾股定理可得:
球心到底面的距离为,
所以正四棱锥P﹣ABCD的高为或,
所以正四棱锥 P﹣ABCD的体积为或.
17.(2025春 万州区期中)如图所示的几何体的上部是一个正四棱锥P﹣ABCD,下部是一个正方体,其中正四棱锥P﹣ABCD的高为,△PCD是等边三角形,CD=6.
(1)求该几何体的表面积;
(2)求该几何体的体积.
【解答】解:(1)设M是CD的中点,连接PM,
因为△PCD是边长为6的正三角形,
所以PM⊥CD,且,
所以该几何体的表面积;
(2)连接AC,BD,设交点为O,连接PO,则PO是四棱锥 P﹣ABCD的高,
则,
所以,
又正方体的体积为6×6×6=216,
所以该几何体的体积.
18.(2025春 岳麓区校级月考)如图,圆锥PO的底面半径和高均是a.
(1)过线段PO的中点O′作平行于底面的截面,以该截面为底面挖去一个圆柱,求剩下几何体的体积.
(2)若过线段PO上的任意一点作平行于底面的截面,并以该截面为底面挖去一个圆柱,求剩下几何体的最大表面积.
【解答】解:(1)如图,设圆锥母线PB与圆柱交点为A,连接O′A,则PO=OB=a,
因为O′为PO中点,
所以圆柱的高OO'POa,圆柱的底面半径O′Aa,
因为圆锥内部挖去一个圆柱,
所以剩下几何体的体积Vππa3.
(2)因为圆锥PO的底面半径和高均是a,
所以圆锥的母线长为,
所以圆锥的表面积S1,
设圆柱的半径为r,高为h,
由题意知,,即,
解得h=a﹣r,
所以圆柱的侧面积S2=2πr h=2πr(a﹣r),
所以剩下几何体的表面积S=S1+S22πr(a﹣r)2π πa2=()πa2,
当且仅当r=a﹣r,即r时,等号成立,
故剩下几何体的最大表面积为()πa2.
19.(2025春 秀英区校级期中)刻画空间的弯曲性是几何研究的重要内容,用曲率刻画空间弯曲性,规定:多面体顶点的曲率等于2π与多面体在该点的面角之和的差(多面体的面的内角叫做多面体的面角,角度用弧度制),例如:正方体在每个顶点有3个面角,每个面角是,所以正方体在各顶点的曲率为,已知四棱锥P﹣ABCD在点A的曲率为,且PB=PD,CB=CD,.
(1)若点B的曲率为,∠PBC=∠ABC,求四棱锥P﹣ABCD的表面积;
(2)若点E在PD上,且PE:ED=2:1.试探究:在棱PC上是否存在点F,使BF∥平面AEC?证明你的结论.
【解答】解:(1)
由,
利用余弦定理可得:,
由∠BAD∈(0,π)可得:,利用内角和定理可得,
此时,
又因为PB=PD,PA=AB=AD,所以△PAD≌△PAB,即∠PAD=∠PAB,
根据四棱锥P﹣ABCD在点A的曲率为,
可得,
利用内角和定理可得,此时
再由点B的曲率为,∠PBC=∠ABC,可得,
因为,所以,又因为CB=CD,所以三角形CBD是等边三角形,
此时,由于,
所以,利用△PBC≌△PDC,
可知,
所以四棱锥P﹣ABCD的表面积为;
(2)证明:
取M,F分别为PE,PC的中点,AC∩BD=O,连接OE,BM,MF,BF,
利用中位线可知MF∥CE,又由CB=CD,AB=AD,可得△ABC≌△ADC,
即∠BAC=∠DAC,又可证得△ABO≌△ADO,即BO=OD,又因为E为MD中点,
所以OE∥BM,又因为OE 平面AEC,BMd平面AEC,
所以BM∥平面AEC,同理由MF∥CE,可证明MF∥平面AEC,
又因为BM∩MF=M,BM,MF 平面BMF,所以平面BMF∥平面AEC,
又因为BF 平面BMF,所以BF∥平面AEC,此时F为PC的中点.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
- 第六章 平面向量及其应用
- 6.1 平面向量的概念
- 6.2 平面向量的运算
- 6.3 平面向量基本定理及坐标表示
- 6.4 平面向量的应用
- 第七章 复数
- 7.1 复数的概念
- 7.2 复数的四则运算
- 7.3 * 复数的三角表示
- 第八章 立体几何初步
- 8.1 基本立体图形
- 8.2 立体图形的直观图
- 8.3 简单几何体的表面积与体积
- 8.4 空间点、直线、平面之间的位置关系
- 8.5 空间直线、平面的平行
- 8.6 空间直线、平面的垂直
- 第九章 统计
- 9.1 随机抽样
- 9.2 用样本估计总体
- 9.3 统计分析案例 公司员工
- 第十章 概率
- 10.1 随机事件与概率
- 10.2 事件的相互独立性
- 10.3 频率与概率
