第九章变量之间的关系期末单元复习题(含解析)
文档属性
| 名称 | 第九章变量之间的关系期末单元复习题(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 724.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 16:24:17 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
第九章变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一本笔记本5元,买x本共付y元,则常量和变量分别是( )
A.常量:5;变量:x B.常量:5;变量:y
C.常量:5;变量:x,y D.常量:x,y;变量:5
2.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
3.刘师傅到加油站加油,如图是所用的加油机上的数据显示牌,则其中的变量是( )
A.金额 B.单价 C.数量 D.金额和数量
4.弹簧挂上物体后会伸长,测得一弹簧的长度(cm)与所挂的物体的质量(kg)间有下面的关系:
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为4kg时,弹簧长度为12cm
C.弹簧不挂重物时的长度为0cm
D.与之间的关系式为
5.高原反应是人到达一定海拔高度后,由于机体对低压低氧环境的适应能力不足而引起的.下面是反映海拔高度与空气含氧量之间关系的一组数据:
海拔高度 0 1000 2000 3000 4000
空气含氧量
下列说法不正确的是( )
A.海拔高度是自变量,空气含氧量是因变量;
B.海拔高度每上升,空气含氧量减少;
C.在海拔高度为的地方空气含氧量是;
D.当海拔高度从上升到时,空气含氧量减少了.
6.在探究水沸腾时温度变化特点的实验中,下表记录了实验中水的温度()随时间(min)变化的数据.若温度的变化是均匀的,则时的水温是( )
时间/min 0 5 10 15 20 25
温度/℃ 10 25 40 55 70 85
A.62 B.64 C.66 D.68
7.小明想用实验的方法测量某种食用油的沸点,他找到一个秒表和一支刻度标有0—100℃的温度计.他在锅中加入一定量的这种食用油,在煤气灶上加热,并且每隔10秒测一次温度,他发现加热到第100秒时,油沸腾了.以下是他的测量数据:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
下面说法不正确的是( )
A.加热到30秒时油温是70℃
B.估计这种食用油的沸点温度是210℃
C.在这个问题中,时间和油温都是变量,其中油温是自变量
D.在一定范围内,每加热10秒,油温上升20℃
8.在实验课上,小亮利用同一块木板测得小车从不同高度()与下滑的时间()的关系如下表:
支撑物高 10 20 30 40 50 …
下滑时间 3.25 3.01 2.81 2.66 2.56 …
以下结论错误的是( )
A.当时,约2.66秒
B.随高度增加,下滑时间越来越短
C.估计当时,一定小于2.56秒
D.高度每增加,时间就会减少0.24秒
9.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下:
温度(℃) 0 10 20 30
声速() 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越低,声速越慢
C.当温度每升高时,声速增加
D.当空气温度为时,声音可以传播
10.某超市苹果的单价是3元/斤,若购买x斤苹果的总价是y元,则其中的常量是( )
A.3 B.x C.y D.不确定
11.清明假期,刘老师乘车从学校到井冈山观赏映山红,缅怀革命先烈.已知学校距离井冈山,车行驶的平均速度为,后刘老师距离井冈山,则与之间的关系式是( )
A. B.
C. D.
12.某种气体在时的体积为,温度每升高,它的体积增加,则该气体的体积与温度之间的函数表达式是( )
A. B.
C. D.
二、填空题
13.已知,变量x、y满足,用x的代数式表示y得 .
14.一个水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
据估计这种上涨规律还会持续2h,预测再过2h水位高度将为 m.
15.以固定的速度(米秒)向上抛一个小球,小球的高度(米)与小球的运动时间(秒)之间的关系是,在这个关系式中,常量是 ,变量是 .
16.如图,若用n表示正方形个数,y表示摆放正方形所用火柴棒根数,则y与n之间的关系式为 .
17.某汽车生产厂对其生产的A型汽车进行油耗试验(油箱已加满),试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时) 0 1 2 3
y(升) 80 72 64 56
如果此辆汽车在行驶6小时后加油一次,将油箱加满,此后继续行驶,由表格中y与t的关系可知,当汽车行驶10小时时:油箱的余油量为 升.
三、解答题
18.下表是某河流在汛期一天中涨水的情况,警戒水位为米.
时间/时 0 4 8
超警戒水位/米
(1)上表反映了________与时间之间的关系,其中____是自变量,______是因变量;
(2)估计上午时的水位是_______;
(3)从0时到时,水位从_______上升到_____;
(4)从__时到__时,水位上升最快;
(5)假设第二天持续下雨(基本与当天降水量一样),则第二天12时超警戒水位__米.
19.圆周长C与圆的半径r之间的关系为.对于各种不同大小的圆.指出中的变量和常量.
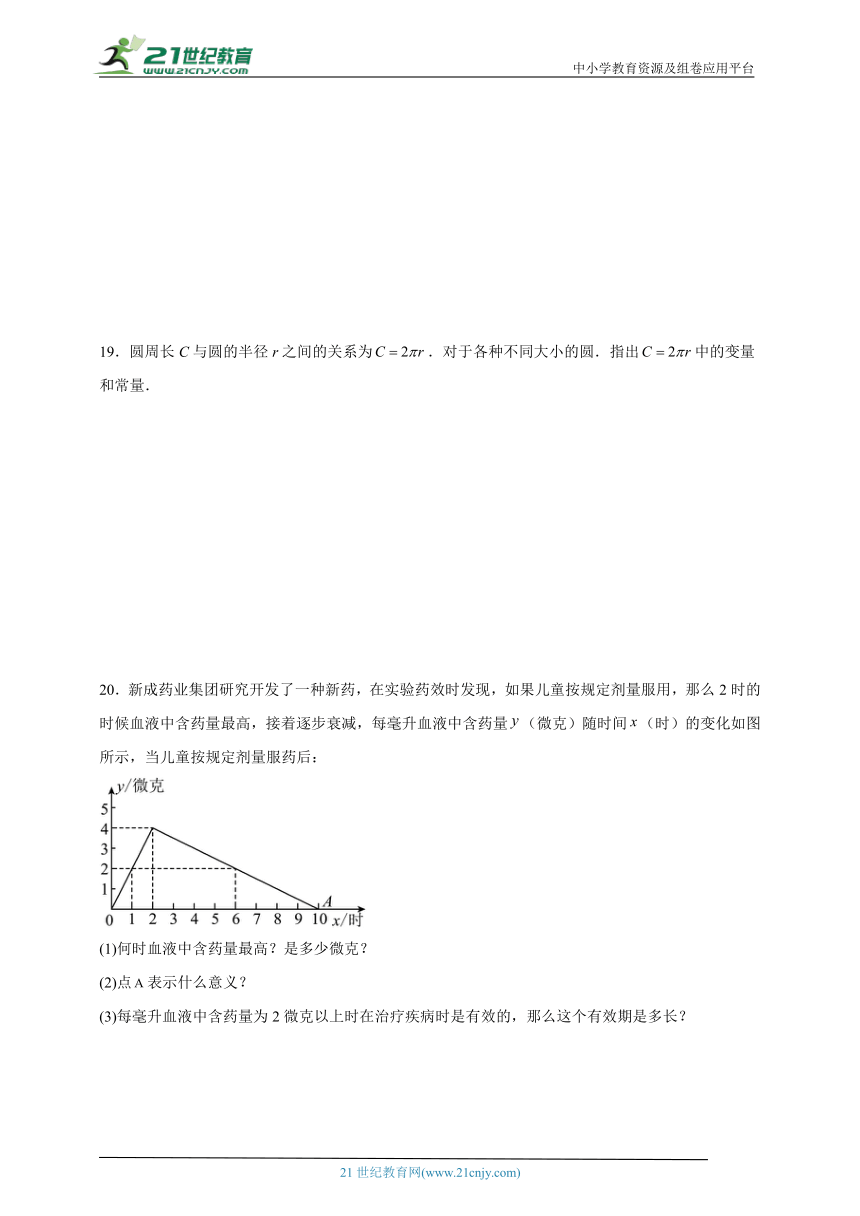
20.新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量(微克)随时间(时)的变化如图所示,当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)点表示什么意义?
(3)每毫升血液中含药量为2微克以上时在治疗疾病时是有效的,那么这个有效期是多长?
21.某水果店橘子的单价为4.5元/千克,记买k千克橘子的总价为s元.说出其中的常量和变量.
22.下表记录的是某橘农去年橘子的销售额(元)随橘子销量(千克)变化的有关数据,请根据表中数据回答下列问题:
销量(千克) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)表格反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当销量是5千克时,销售额是多少?
(3)估计当销量是50千克时,销售额是多少?
23.下表是某同学做的“观察水的沸腾”实验时所记录的数据,实验过程共加热15分钟:
时间(分) 0 1 2 3 4 5 6 7 8 9 10 11
温度(℃) 20 30 40 50 60 70 80 90 100 100 100 100
(1)上表反映了哪两个变量之间的关系?
(2)根据表格,你认为12分钟、13分钟时,水的温度是多少?
(3)为了节约能源,你认为烧开水的时候应该在大约几分钟关闭煤气?
24.如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.8厘米,每个铁环长5厘米,设铁环间处于最大限度的拉伸状态.
求:(1)2个、3个、4个铁环组成的链条长分别有多少.
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.09米长的链条,需要多少个铁环?
《第九章变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C B B C D D A
题号 11 12
答案 A A
1.C
【分析】在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,所以5是常量,、是变量,据此判断即可.
【详解】解:一本笔记本5元,买本共付元,则5是常量,、是变量.
故选:C.
【点睛】此题主要考查了常量与变量问题,解题的关键是要明确:常量与变量必须存在于同一个变化过程中,判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化.
2.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
3.D
【分析】本题考查了常量和变量.根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量即可求解.
【详解】解:在金额、数量和单价中,金额和数量是变量,单价是常量.
故选:D.
4.C
【分析】根据挂重物与弹簧伸长的长度,可得答案.
【详解】解:A、x和y都是变量,且x是自变量,y是因变量,故A正确;
B、当时,,故B正确;
C、当时,,故C错误;
D、由挂重物与弹簧伸长的长度,得,故D正确;
故选:C.
【点睛】本题考查了函数关系式,利用挂重物与弹簧伸长的长度得出函数关系式是解题关键.
5.B
【分析】本题主要考查了用表格表示变量,解题的关键是,熟练掌握自变量和因变量,表中数据及变化.
根据题目中表格给出的数据逐一判断,即可.
【详解】A.海拔高度是自变量,空气含氧量是因变量;
∵海拔高度是自变量,空气含氧量是因变量,
∴A正确,不符合题意;
B.海拔高度每上升,空气含氧量减少;
∵,,,,
∴海拔高度每上升,空气含氧量减少值不都是,
∴B错误,符合题意.
C.在海拔高度为的地方空气含氧量是;
∵在海拔高度为的地方空气含氧量是,
∴C正确,不符合题意;
D.当海拔高度从上升到时,空气含氧量减少了;
由B知,当海拔高度从上升到时,空气含氧量减少了,
∴D正确,不符合题意.
故选:B.
6.B
【分析】本题考查了函数关系的应用;
根据表格求出时间每增加,水温上升,再根据时水温是55进行计算即可.
【详解】解:由表格知:时间每增加,水温上升15,
∴时间每增加,水温上升,
∵时水温是55,
∴时的水温是,
故选:B.
7.C
【分析】根据表格中两个变量的变化关系以及对应值逐项进行判断即可.
【详解】解:A.由表格中的数据可知,当时间为30秒时,所对应的油温是70℃,说法正确,不符合题意;
B.根据表格中油温随时间的变化规律可得,当时间为100秒时,所对应的油温为10+20×=210℃,说法正确,不符合题意;
C.由题意可知,在这个问题中,时间和油温都是变量,其中时间是自变量,油温是因变量,原说法错误,符合题意;
D.由表格中的两个变量变化的对应值可得,在一定范围内,每加热10秒,油温上升20℃,说法正确,不符合题意;
故选:C.
【点睛】本题考查变量与常量,函数的表示方法,理解表格中油温随时间的变化规律是正确判断的前提.
8.D
【分析】根据表格的数据,逐项分析即可得到答案.
【详解】解:A、由表格可知:当时,约2.66秒,故A选项正确,不符合题意;
B、由表格可知:当由10逐渐增大到50时,的值由3.25逐渐减小到2.56,因此随高度增加,下滑时间越来越短,故B选项正确,不符合题意;
C、由B可知:随高度增加,下滑时间越来越短,且当时,,所以估计当时,一定小于2.56秒,故C选项正确,不符合题意;
D、由表格可知:时间的减少是不均匀的,故D选项错误,符合题意;
故选:D.
【点睛】本题主要考查了用表格表示变量间的关系,依据表格反映的规律回答问题是解题的关键.
9.D
【分析】本题考查用表格表示变量之间的关系,从表格中获取信息,逐一进行分析即可.
【详解】解:A.∵在这个变化中,自变量是温度,因变量是声速,∴说法正确,不符合题意;
B.∵根据表中数据,可得温度越低,声速越慢,∴说法正确,不符合题意;
C.∵,,,,,
∴当温度每升高,声速增加,∴说法正确,不符合题意;
D.∵,
∴当空气温度为时,声音可以传播,∴说法错误,符合题意.
故选:D.
10.A
【分析】本题主要考查了常量与变量的区别,常量就是数值始终不变的量,变量是数值发生变化的量,根据总价=单价×数量列式,再根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量解答.
【详解】解: 某超市苹果的单价是3元/斤,若购买x斤苹果的总价是y元,则其中的常量是3,
故选:A.
11.A
【分析】本题考查用关系式表示变量间的关系,根据“路程、速度、时间”之间的关系解答即可;
【详解】解:根据题意有:,
故选:A.
12.A
【分析】本题主要考查了列函数关系式,该气体的体积等于温度为时的体积加上在的基础上上升的温度乘以即可得到体积与温度之间的函数表达式.
【详解】解:由题意得,,
故选:A.
13.///
【分析】根据等式的性质进行化简即可求出答案.
【详解】解:,
,
,
,
故答案为:.
【点睛】本题考查变量之间的关系.解题的关键是熟练运用等式的性质,本题属于基础题型.
14.5.1
【分析】由题意可得到水位随时间上涨的速度,即可求出再过2h水位高度.
【详解】由表格可知,每小时水库的水位上涨0.3m,
所以2h水库的水位上涨m,
m.
故答案为:5.1.
【点睛】此题考查了变量之间的关系,解题的关键是分析出题目中变量之间的关系.
15. , ,
【分析】本题考查了常量与变量,熟练掌握常量与变量的定义是解题的关键:在一个变化过程中,数值始终不变的量称为常量;在某一变化过程中,数值发生变化的量称为变量.
根据常量与变量的定义即可直接得出答案.
【详解】解:由常量与变量的定义可知:
在关系式中,常量是,,变量是,,
故答案为:,;,.
16.
【分析】根据“所用火柴棒的根数”与“所摆正方形的个数”之间的变化关系,得出答案.
【详解】第1个图形需要火柴棒根数为,
第2个图形需要火柴棒根数为,
第3个图形需要火柴棒根数为,
……
第n个图形需要火柴棒根数为,
y与n之间的关系式为,
故答案为:.
【点睛】本题考查函数关系式,图形的变化类,理解函数的定义,发现“所用火柴棒的根数与所摆正方形的个数”之间的变化规律是解决问题的前提.
17.48
【分析】由表格中的数据可得:汽车每行驶1小时,耗油8升,由于汽车已经行驶了6小时,油箱加满后,只要再计算出汽车行驶4小时的耗油量,即得剩余油量.
【详解】解:由表格中的数据可得:汽车每行驶1小时,耗油8升,
此辆汽车在行驶6小时后加油一次,将油箱加满,此时油箱中有油80升,
所以,当汽车行驶10小时时,即再行驶4小时,耗油升,则油箱的余油量为升;
故答案为:48.
【点睛】本题考查了列表法表示变量之间的关系,正确理解题意是关键.
18.(1)超警戒水位,时间,超警戒水位
(2)米
(3)米,米
(4),
(5)
【分析】(1)上表反映了超警戒水位与时间之间的关系,其中时间是自变量,超警戒水位是因变量;
(2)由表格数据即可得;
(3)观察表格,计算出0时水位,时水位即可得;
(4)借助表格,算出在4至8时,警戒水位上升,在8至时,警戒水位上升,从时到时,在至时,警戒水位上升,在至时,警戒水位上升,在至时,警戒水位上升,即可得;
(5)观察表格得,第一天时超警戒水位米,时警戒水位米,假若第二天持续下雨(基本与第一天降水情况一样),则估计第二天时超警戒水位米.
【详解】(1)解:上表反映了超警戒水位随着时间的变化而变化,其中时间是自变量,超警戒水位是因变量;
(2)解:估计上午时超警戒水位米,
则估计上午时的水位是: (米),
故答案为:米;
(3)解:0时水位:(米)
时水位:(米),
即从0时到时,水位从米上升到米,
故答案为:米,米;
(4)解:观察表格得,在0至4时,警戒水位上升:(米),
在4至8时,警戒水位上升:(米),
在8至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
即从时到时,水位上升的最快,
故答案为:,;
(5)解:观察表格得,第一天时超警戒水位米,时警戒水位米,
假若第二天持续下雨(基本与第一天降水情况一样),
则估计第二天时超警戒水位(米),
故答案为:.
【点睛】本题考查了常量与变量,有理数的加减法,解题的关键是掌握这些知识点,正确计算.
19.变量为C与r,常量为
【分析】一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有为一得值与其对应,那么我们就说x是自变量,所以上述过程中,自变量是半径.
【详解】解:根据题意得:中的变量为C与r,常量为.
【点睛】本题主要考查了常量与变量问题,熟练掌握常量与变量必须存在于同一个变化过程中,判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化是解题的关键.
20.(1)服药后2时;4微克
(2)服药后10时,每毫升血液中不含此药
(3)5小时
【分析】本题考查用图象表示变量之间的关系,解题的关键在于根据图象获取需要的信息求解.
(1)根据图中信息回答即可;
(2) 根据图中信息回答即可;
(3)服药后每毫升血液中含药量达到2微克的时间是1时,衰减到2微克的时间是6时,据此计算出有效时间即可.
【详解】(1)解:由图可知,服药后2时血液中含药量最高,是4微克;
(2)解:点表示当时间为10时,每毫升血液中含药量为0微克,即服药后10时,每毫升血液中不含此药;
(3)解:由图知,这个有效期为(时),
这个有效期为5小时.
21.变量:k,s,常量:4.5.
【分析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可直接得到答案.
【详解】由题意得:s=4.5k,
变量:k,s,常量:4.5.
【点睛】本题考查了函数关系式的求法与常量和变量的定义,常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.
22.(1)表格反映了橘子的销量与销售额之间的关系,橘子的销量是自变量,销售额是因变量
(2)当销量是5千克时,销售额是10元
(3)当销量是50千克时,销售额是100元
【分析】本题主要考查自变量与因变量的关系,理解表示信息,确定销量与销售额的关系是解题的关键.
(1)根据销量与销售额的变化情况分析即可;
(2)由表格信息即可求解;
(3)根据表格信息得到销量与销售额的关系即可求解.
【详解】(1)解:根据题意,销量在增加,销售额随之增大,
∴表格反映了橘子的销量与销售额之间的关系,橘子的销量是自变量,销售额是因变量;
(2)解:根据表格信息可得,当销量是5千克时,销售额是10元;
(3)解:根据题意,销售额是销量的2倍,
∴当销量是50千克时,销售额是100元.
23.(1)水的温度与时间的关系
(2)
(3)8分钟
【分析】此题主要考查了常量与变量,根据表格中数据分别分析得出是解题关键.
(1)在函数中,给一个变量x一个值,另一个变量y就有唯一对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度,进而可得出时间为12、13分钟时,水的温度;
(3)根据表格中数据得出答案即可.
【详解】(1)解:上表反映了水的温度与时间的关系;
(2)解:根据表格,可得:时间为12分钟和13分钟时,水的温度是;
(3)解:为了节约能源,烧开水的时候应该在大约8分钟关闭煤气.
24.(1)2个铁环组成的链条长,3个铁环组成的链条长为,4个铁环组成的链条长;(2);(3)需要61个铁环
【分析】(1)根据铁环粗0.8厘米,每个铁环长5厘米,进而得出2个、3个、4个铁环组成的链条长;
(2)根据铁环与环长之间的关系进而得出y与n的关系式;
(3)由(2)得,3.4n+1.6=209,进而求出即可.
【详解】解:(1)由题意可得:,
,
.
故2个铁环组成的链条长,3个铁环组成的链条长为,4个铁环组成的链条长;
(2)由题意得:n个铁环一共有n-1个相接的地方,
∴,
即;
(3)∵2.09米
∴据题意有,
解得:,
答:需要61个铁环.
【点睛】本题主要考查了用关系式表示的变量之间的关系,利用链条结构得出链条长的变化规律是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第九章变量之间的关系
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.一本笔记本5元,买x本共付y元,则常量和变量分别是( )
A.常量:5;变量:x B.常量:5;变量:y
C.常量:5;变量:x,y D.常量:x,y;变量:5
2.甲、乙两车沿同一条路从地出发匀速行驶至相距的地,甲出发1小时后乙再出发,如图表示甲、乙两车离开地的距离与乙出发的时间之间的关系,下列结论错误的是( )
A.甲车的速度是 B.乙车的速度是
C.的值为60,的值为4 D.甲车出发后被乙车追上
3.刘师傅到加油站加油,如图是所用的加油机上的数据显示牌,则其中的变量是( )
A.金额 B.单价 C.数量 D.金额和数量
4.弹簧挂上物体后会伸长,测得一弹簧的长度(cm)与所挂的物体的质量(kg)间有下面的关系:
0 1 2 3 4 5
10 10.5 11 11.5 12 12.5
下列说法不正确的是( )
A.与都是变量,且是自变量,是因变量
B.所挂物体质量为4kg时,弹簧长度为12cm
C.弹簧不挂重物时的长度为0cm
D.与之间的关系式为
5.高原反应是人到达一定海拔高度后,由于机体对低压低氧环境的适应能力不足而引起的.下面是反映海拔高度与空气含氧量之间关系的一组数据:
海拔高度 0 1000 2000 3000 4000
空气含氧量
下列说法不正确的是( )
A.海拔高度是自变量,空气含氧量是因变量;
B.海拔高度每上升,空气含氧量减少;
C.在海拔高度为的地方空气含氧量是;
D.当海拔高度从上升到时,空气含氧量减少了.
6.在探究水沸腾时温度变化特点的实验中,下表记录了实验中水的温度()随时间(min)变化的数据.若温度的变化是均匀的,则时的水温是( )
时间/min 0 5 10 15 20 25
温度/℃ 10 25 40 55 70 85
A.62 B.64 C.66 D.68
7.小明想用实验的方法测量某种食用油的沸点,他找到一个秒表和一支刻度标有0—100℃的温度计.他在锅中加入一定量的这种食用油,在煤气灶上加热,并且每隔10秒测一次温度,他发现加热到第100秒时,油沸腾了.以下是他的测量数据:
时间t/s 0 10 20 30 40
油温y/℃ 10 30 50 70 90
下面说法不正确的是( )
A.加热到30秒时油温是70℃
B.估计这种食用油的沸点温度是210℃
C.在这个问题中,时间和油温都是变量,其中油温是自变量
D.在一定范围内,每加热10秒,油温上升20℃
8.在实验课上,小亮利用同一块木板测得小车从不同高度()与下滑的时间()的关系如下表:
支撑物高 10 20 30 40 50 …
下滑时间 3.25 3.01 2.81 2.66 2.56 …
以下结论错误的是( )
A.当时,约2.66秒
B.随高度增加,下滑时间越来越短
C.估计当时,一定小于2.56秒
D.高度每增加,时间就会减少0.24秒
9.某科研小组在网上获取了声音在空气中传播的速度与空气温度关系的一些数据如下:
温度(℃) 0 10 20 30
声速() 318 324 330 336 342 348
下列说法错误的是( )
A.在这个变化中,自变量是温度,因变量是声速
B.温度越低,声速越慢
C.当温度每升高时,声速增加
D.当空气温度为时,声音可以传播
10.某超市苹果的单价是3元/斤,若购买x斤苹果的总价是y元,则其中的常量是( )
A.3 B.x C.y D.不确定
11.清明假期,刘老师乘车从学校到井冈山观赏映山红,缅怀革命先烈.已知学校距离井冈山,车行驶的平均速度为,后刘老师距离井冈山,则与之间的关系式是( )
A. B.
C. D.
12.某种气体在时的体积为,温度每升高,它的体积增加,则该气体的体积与温度之间的函数表达式是( )
A. B.
C. D.
二、填空题
13.已知,变量x、y满足,用x的代数式表示y得 .
14.一个水库的水位在最近5h内持续上涨,下表记录了这5h内6个时间点的水位高度,其中t表示时间,y表示水位高度.
t/h 0 1 2 3 4 5
y/m 3 3.3 3.6 3.9 4.2 4.5
据估计这种上涨规律还会持续2h,预测再过2h水位高度将为 m.
15.以固定的速度(米秒)向上抛一个小球,小球的高度(米)与小球的运动时间(秒)之间的关系是,在这个关系式中,常量是 ,变量是 .
16.如图,若用n表示正方形个数,y表示摆放正方形所用火柴棒根数,则y与n之间的关系式为 .
17.某汽车生产厂对其生产的A型汽车进行油耗试验(油箱已加满),试验中汽车为匀速行驶,在行驶过程中,油箱的余油量y(升)与行驶时间t(小时)之间的关系如下表:
t(小时) 0 1 2 3
y(升) 80 72 64 56
如果此辆汽车在行驶6小时后加油一次,将油箱加满,此后继续行驶,由表格中y与t的关系可知,当汽车行驶10小时时:油箱的余油量为 升.
三、解答题
18.下表是某河流在汛期一天中涨水的情况,警戒水位为米.
时间/时 0 4 8
超警戒水位/米
(1)上表反映了________与时间之间的关系,其中____是自变量,______是因变量;
(2)估计上午时的水位是_______;
(3)从0时到时,水位从_______上升到_____;
(4)从__时到__时,水位上升最快;
(5)假设第二天持续下雨(基本与当天降水量一样),则第二天12时超警戒水位__米.
19.圆周长C与圆的半径r之间的关系为.对于各种不同大小的圆.指出中的变量和常量.
20.新成药业集团研究开发了一种新药,在实验药效时发现,如果儿童按规定剂量服用,那么2时的时候血液中含药量最高,接着逐步衰减,每毫升血液中含药量(微克)随时间(时)的变化如图所示,当儿童按规定剂量服药后:
(1)何时血液中含药量最高?是多少微克?
(2)点表示什么意义?
(3)每毫升血液中含药量为2微克以上时在治疗疾病时是有效的,那么这个有效期是多长?
21.某水果店橘子的单价为4.5元/千克,记买k千克橘子的总价为s元.说出其中的常量和变量.
22.下表记录的是某橘农去年橘子的销售额(元)随橘子销量(千克)变化的有关数据,请根据表中数据回答下列问题:
销量(千克) 1 2 3 4 5 6 7 8 9
销售额(元) 2 4 6 8 10 12 14 16 18
(1)表格反映了哪两个变量之间的关系?哪个是自变量?哪个是因变量?
(2)当销量是5千克时,销售额是多少?
(3)估计当销量是50千克时,销售额是多少?
23.下表是某同学做的“观察水的沸腾”实验时所记录的数据,实验过程共加热15分钟:
时间(分) 0 1 2 3 4 5 6 7 8 9 10 11
温度(℃) 20 30 40 50 60 70 80 90 100 100 100 100
(1)上表反映了哪两个变量之间的关系?
(2)根据表格,你认为12分钟、13分钟时,水的温度是多少?
(3)为了节约能源,你认为烧开水的时候应该在大约几分钟关闭煤气?
24.如图,是若干个粗细均匀的铁环最大限度的拉伸组成的链条,已知铁环粗0.8厘米,每个铁环长5厘米,设铁环间处于最大限度的拉伸状态.
求:(1)2个、3个、4个铁环组成的链条长分别有多少.
(2)设n个铁环长为y厘米,请用含n的式子表示y;
(3)若要组成2.09米长的链条,需要多少个铁环?
《第九章变量之间的关系》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C D D C B B C D D A
题号 11 12
答案 A A
1.C
【分析】在一个变化的过程中,数值发生变化的量称为变量,数值始终不变的量称为常量,所以5是常量,、是变量,据此判断即可.
【详解】解:一本笔记本5元,买本共付元,则5是常量,、是变量.
故选:C.
【点睛】此题主要考查了常量与变量问题,解题的关键是要明确:常量与变量必须存在于同一个变化过程中,判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化.
2.D
【分析】根据图象,列出关于a,b的方程,求出a,b的值,从而即可逐一判断各个选项.
【详解】解:根据图象可知,(300-a)÷b=(240-a)÷3=a÷1,
解得:a=60,b=4,
甲车的速度=60÷1=60km/h,乙车的速度=300÷3=100km/h,
故A,B,C正确,不符合题意;
∵60÷(100-60)=1.5,1.5+1=2.5h,
∴甲车出发后被乙车追上,
故D错误,符合题意,
故选D.
【点睛】本题考查了用图像表示的变量间关系,理解图象以及分别求出甲、乙两人的速度是解题的关键.
3.D
【分析】本题考查了常量和变量.根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量即可求解.
【详解】解:在金额、数量和单价中,金额和数量是变量,单价是常量.
故选:D.
4.C
【分析】根据挂重物与弹簧伸长的长度,可得答案.
【详解】解:A、x和y都是变量,且x是自变量,y是因变量,故A正确;
B、当时,,故B正确;
C、当时,,故C错误;
D、由挂重物与弹簧伸长的长度,得,故D正确;
故选:C.
【点睛】本题考查了函数关系式,利用挂重物与弹簧伸长的长度得出函数关系式是解题关键.
5.B
【分析】本题主要考查了用表格表示变量,解题的关键是,熟练掌握自变量和因变量,表中数据及变化.
根据题目中表格给出的数据逐一判断,即可.
【详解】A.海拔高度是自变量,空气含氧量是因变量;
∵海拔高度是自变量,空气含氧量是因变量,
∴A正确,不符合题意;
B.海拔高度每上升,空气含氧量减少;
∵,,,,
∴海拔高度每上升,空气含氧量减少值不都是,
∴B错误,符合题意.
C.在海拔高度为的地方空气含氧量是;
∵在海拔高度为的地方空气含氧量是,
∴C正确,不符合题意;
D.当海拔高度从上升到时,空气含氧量减少了;
由B知,当海拔高度从上升到时,空气含氧量减少了,
∴D正确,不符合题意.
故选:B.
6.B
【分析】本题考查了函数关系的应用;
根据表格求出时间每增加,水温上升,再根据时水温是55进行计算即可.
【详解】解:由表格知:时间每增加,水温上升15,
∴时间每增加,水温上升,
∵时水温是55,
∴时的水温是,
故选:B.
7.C
【分析】根据表格中两个变量的变化关系以及对应值逐项进行判断即可.
【详解】解:A.由表格中的数据可知,当时间为30秒时,所对应的油温是70℃,说法正确,不符合题意;
B.根据表格中油温随时间的变化规律可得,当时间为100秒时,所对应的油温为10+20×=210℃,说法正确,不符合题意;
C.由题意可知,在这个问题中,时间和油温都是变量,其中时间是自变量,油温是因变量,原说法错误,符合题意;
D.由表格中的两个变量变化的对应值可得,在一定范围内,每加热10秒,油温上升20℃,说法正确,不符合题意;
故选:C.
【点睛】本题考查变量与常量,函数的表示方法,理解表格中油温随时间的变化规律是正确判断的前提.
8.D
【分析】根据表格的数据,逐项分析即可得到答案.
【详解】解:A、由表格可知:当时,约2.66秒,故A选项正确,不符合题意;
B、由表格可知:当由10逐渐增大到50时,的值由3.25逐渐减小到2.56,因此随高度增加,下滑时间越来越短,故B选项正确,不符合题意;
C、由B可知:随高度增加,下滑时间越来越短,且当时,,所以估计当时,一定小于2.56秒,故C选项正确,不符合题意;
D、由表格可知:时间的减少是不均匀的,故D选项错误,符合题意;
故选:D.
【点睛】本题主要考查了用表格表示变量间的关系,依据表格反映的规律回答问题是解题的关键.
9.D
【分析】本题考查用表格表示变量之间的关系,从表格中获取信息,逐一进行分析即可.
【详解】解:A.∵在这个变化中,自变量是温度,因变量是声速,∴说法正确,不符合题意;
B.∵根据表中数据,可得温度越低,声速越慢,∴说法正确,不符合题意;
C.∵,,,,,
∴当温度每升高,声速增加,∴说法正确,不符合题意;
D.∵,
∴当空气温度为时,声音可以传播,∴说法错误,符合题意.
故选:D.
10.A
【分析】本题主要考查了常量与变量的区别,常量就是数值始终不变的量,变量是数值发生变化的量,根据总价=单价×数量列式,再根据在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量解答.
【详解】解: 某超市苹果的单价是3元/斤,若购买x斤苹果的总价是y元,则其中的常量是3,
故选:A.
11.A
【分析】本题考查用关系式表示变量间的关系,根据“路程、速度、时间”之间的关系解答即可;
【详解】解:根据题意有:,
故选:A.
12.A
【分析】本题主要考查了列函数关系式,该气体的体积等于温度为时的体积加上在的基础上上升的温度乘以即可得到体积与温度之间的函数表达式.
【详解】解:由题意得,,
故选:A.
13.///
【分析】根据等式的性质进行化简即可求出答案.
【详解】解:,
,
,
,
故答案为:.
【点睛】本题考查变量之间的关系.解题的关键是熟练运用等式的性质,本题属于基础题型.
14.5.1
【分析】由题意可得到水位随时间上涨的速度,即可求出再过2h水位高度.
【详解】由表格可知,每小时水库的水位上涨0.3m,
所以2h水库的水位上涨m,
m.
故答案为:5.1.
【点睛】此题考查了变量之间的关系,解题的关键是分析出题目中变量之间的关系.
15. , ,
【分析】本题考查了常量与变量,熟练掌握常量与变量的定义是解题的关键:在一个变化过程中,数值始终不变的量称为常量;在某一变化过程中,数值发生变化的量称为变量.
根据常量与变量的定义即可直接得出答案.
【详解】解:由常量与变量的定义可知:
在关系式中,常量是,,变量是,,
故答案为:,;,.
16.
【分析】根据“所用火柴棒的根数”与“所摆正方形的个数”之间的变化关系,得出答案.
【详解】第1个图形需要火柴棒根数为,
第2个图形需要火柴棒根数为,
第3个图形需要火柴棒根数为,
……
第n个图形需要火柴棒根数为,
y与n之间的关系式为,
故答案为:.
【点睛】本题考查函数关系式,图形的变化类,理解函数的定义,发现“所用火柴棒的根数与所摆正方形的个数”之间的变化规律是解决问题的前提.
17.48
【分析】由表格中的数据可得:汽车每行驶1小时,耗油8升,由于汽车已经行驶了6小时,油箱加满后,只要再计算出汽车行驶4小时的耗油量,即得剩余油量.
【详解】解:由表格中的数据可得:汽车每行驶1小时,耗油8升,
此辆汽车在行驶6小时后加油一次,将油箱加满,此时油箱中有油80升,
所以,当汽车行驶10小时时,即再行驶4小时,耗油升,则油箱的余油量为升;
故答案为:48.
【点睛】本题考查了列表法表示变量之间的关系,正确理解题意是关键.
18.(1)超警戒水位,时间,超警戒水位
(2)米
(3)米,米
(4),
(5)
【分析】(1)上表反映了超警戒水位与时间之间的关系,其中时间是自变量,超警戒水位是因变量;
(2)由表格数据即可得;
(3)观察表格,计算出0时水位,时水位即可得;
(4)借助表格,算出在4至8时,警戒水位上升,在8至时,警戒水位上升,从时到时,在至时,警戒水位上升,在至时,警戒水位上升,在至时,警戒水位上升,即可得;
(5)观察表格得,第一天时超警戒水位米,时警戒水位米,假若第二天持续下雨(基本与第一天降水情况一样),则估计第二天时超警戒水位米.
【详解】(1)解:上表反映了超警戒水位随着时间的变化而变化,其中时间是自变量,超警戒水位是因变量;
(2)解:估计上午时超警戒水位米,
则估计上午时的水位是: (米),
故答案为:米;
(3)解:0时水位:(米)
时水位:(米),
即从0时到时,水位从米上升到米,
故答案为:米,米;
(4)解:观察表格得,在0至4时,警戒水位上升:(米),
在4至8时,警戒水位上升:(米),
在8至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
在至时,警戒水位上升:(米),
即从时到时,水位上升的最快,
故答案为:,;
(5)解:观察表格得,第一天时超警戒水位米,时警戒水位米,
假若第二天持续下雨(基本与第一天降水情况一样),
则估计第二天时超警戒水位(米),
故答案为:.
【点睛】本题考查了常量与变量,有理数的加减法,解题的关键是掌握这些知识点,正确计算.
19.变量为C与r,常量为
【分析】一般地,在一个变化过程中,如果有两个变量x与y,并且对于x的每一个确定的值,y都有为一得值与其对应,那么我们就说x是自变量,所以上述过程中,自变量是半径.
【详解】解:根据题意得:中的变量为C与r,常量为.
【点睛】本题主要考查了常量与变量问题,熟练掌握常量与变量必须存在于同一个变化过程中,判断一个量是常量还是变量,需要看两个方面:一是它是否在一个变化过程中;二是看它在这个变化过程中的取值情况是否发生变化是解题的关键.
20.(1)服药后2时;4微克
(2)服药后10时,每毫升血液中不含此药
(3)5小时
【分析】本题考查用图象表示变量之间的关系,解题的关键在于根据图象获取需要的信息求解.
(1)根据图中信息回答即可;
(2) 根据图中信息回答即可;
(3)服药后每毫升血液中含药量达到2微克的时间是1时,衰减到2微克的时间是6时,据此计算出有效时间即可.
【详解】(1)解:由图可知,服药后2时血液中含药量最高,是4微克;
(2)解:点表示当时间为10时,每毫升血液中含药量为0微克,即服药后10时,每毫升血液中不含此药;
(3)解:由图知,这个有效期为(时),
这个有效期为5小时.
21.变量:k,s,常量:4.5.
【分析】根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可直接得到答案.
【详解】由题意得:s=4.5k,
变量:k,s,常量:4.5.
【点睛】本题考查了函数关系式的求法与常量和变量的定义,常量就是在变化过程中不变的量,变量就是可以取到不同数值的量.
22.(1)表格反映了橘子的销量与销售额之间的关系,橘子的销量是自变量,销售额是因变量
(2)当销量是5千克时,销售额是10元
(3)当销量是50千克时,销售额是100元
【分析】本题主要考查自变量与因变量的关系,理解表示信息,确定销量与销售额的关系是解题的关键.
(1)根据销量与销售额的变化情况分析即可;
(2)由表格信息即可求解;
(3)根据表格信息得到销量与销售额的关系即可求解.
【详解】(1)解:根据题意,销量在增加,销售额随之增大,
∴表格反映了橘子的销量与销售额之间的关系,橘子的销量是自变量,销售额是因变量;
(2)解:根据表格信息可得,当销量是5千克时,销售额是10元;
(3)解:根据题意,销售额是销量的2倍,
∴当销量是50千克时,销售额是100元.
23.(1)水的温度与时间的关系
(2)
(3)8分钟
【分析】此题主要考查了常量与变量,根据表格中数据分别分析得出是解题关键.
(1)在函数中,给一个变量x一个值,另一个变量y就有唯一对应的值,则x是自变量,y是因变量,据此即可判断;
(2)根据表格中数据得出水的温度,进而可得出时间为12、13分钟时,水的温度;
(3)根据表格中数据得出答案即可.
【详解】(1)解:上表反映了水的温度与时间的关系;
(2)解:根据表格,可得:时间为12分钟和13分钟时,水的温度是;
(3)解:为了节约能源,烧开水的时候应该在大约8分钟关闭煤气.
24.(1)2个铁环组成的链条长,3个铁环组成的链条长为,4个铁环组成的链条长;(2);(3)需要61个铁环
【分析】(1)根据铁环粗0.8厘米,每个铁环长5厘米,进而得出2个、3个、4个铁环组成的链条长;
(2)根据铁环与环长之间的关系进而得出y与n的关系式;
(3)由(2)得,3.4n+1.6=209,进而求出即可.
【详解】解:(1)由题意可得:,
,
.
故2个铁环组成的链条长,3个铁环组成的链条长为,4个铁环组成的链条长;
(2)由题意得:n个铁环一共有n-1个相接的地方,
∴,
即;
(3)∵2.09米
∴据题意有,
解得:,
答:需要61个铁环.
【点睛】本题主要考查了用关系式表示的变量之间的关系,利用链条结构得出链条长的变化规律是解题的关键.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
