第二十章函数期末单元复习题(含解析)
文档属性
| 名称 | 第二十章函数期末单元复习题(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 984.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 16:39:03 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
第二十章函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.王华积极响应《体质管理通知》中的规定:每天坚持校外1小时体育活动时间.已知王华家、体育场、文具店在同一直线上.下图所反映的过程是:王华从家跑步去体育场,锻炼了一阵后,又走到文具店买笔,然后步行回家.图中x表示时间,y表示王华离家的距离.下列说法正确的是( )
A.王华在体育场锻炼的时间和在文具店退留的时间相同
B.体育场与文具店的距离为
C.王华的跑步速度是
D.王华从体育场步行去文具店的速度比从文具店步行回家的速度快
2.使函数y=有意义的自变量x的取值范围是( )
A.x≥6 B.x≥0 C.x≤6 D.x≤0
3.笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量.
上述判断正确的有( )
A.1个 B.2个 C.3个 D.4个
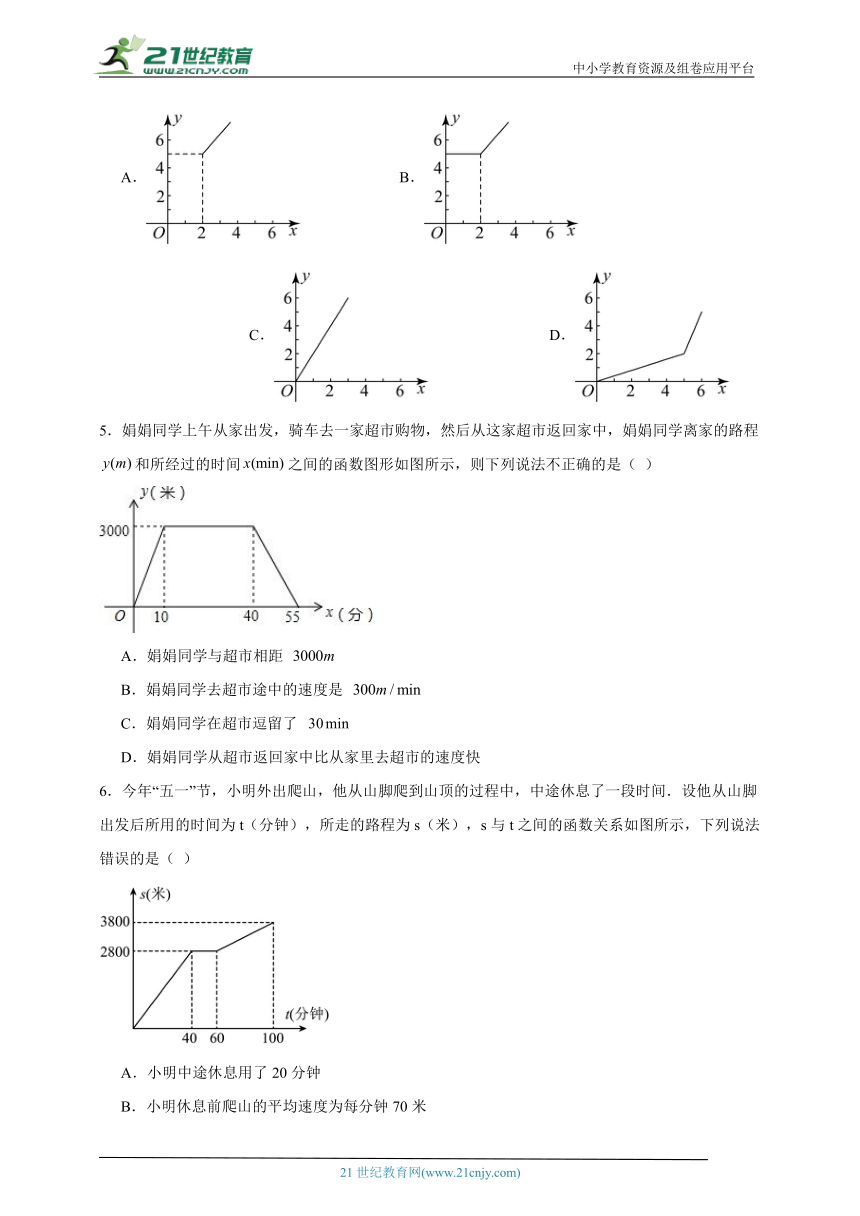
4.某市运货的摩托车的运输价格为:路程2km内运费5元;超过2km后,每1km增加运费1元,那么运费y(单位:元)与路程x(单位:km)的函数图象是( )
A. B. C. D.
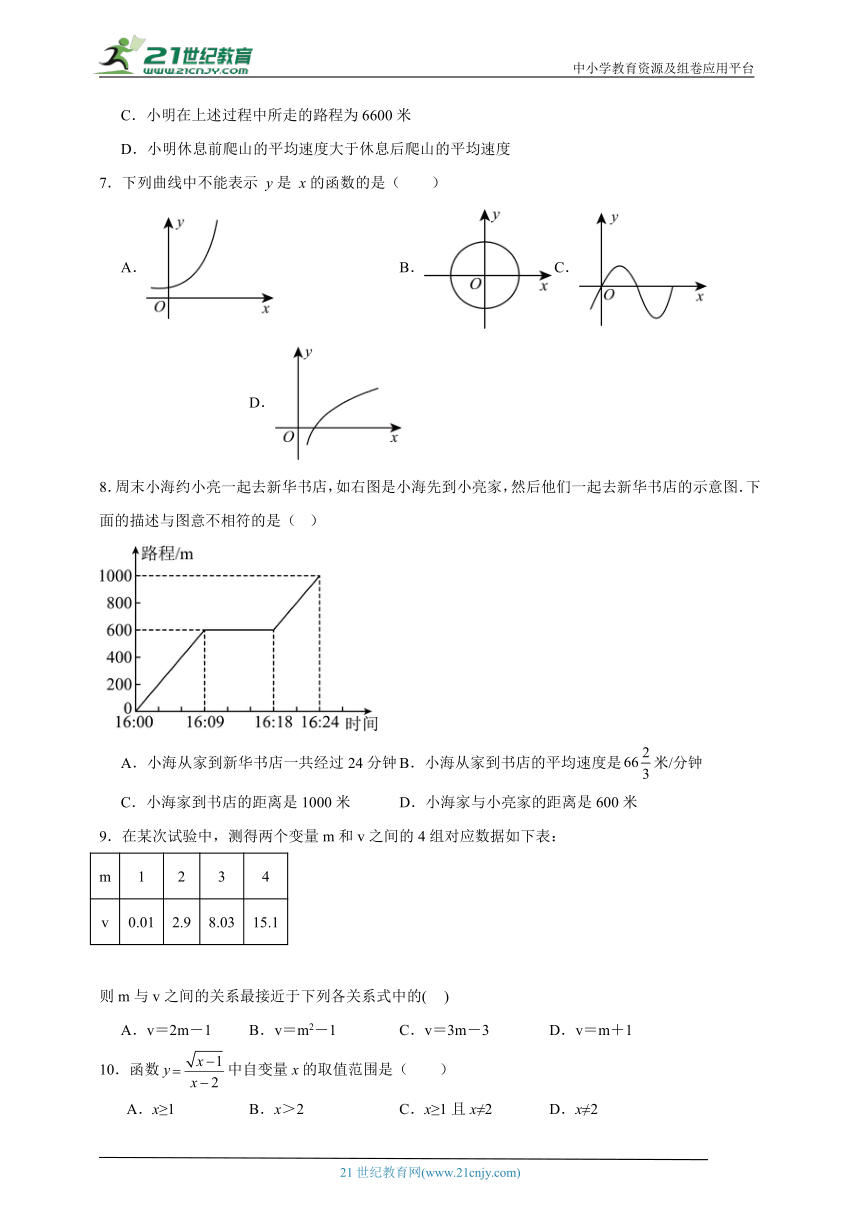
5.娟娟同学上午从家出发,骑车去一家超市购物,然后从这家超市返回家中,娟娟同学离家的路程和所经过的时间之间的函数图形如图所示,则下列说法不正确的是( )
A.娟娟同学与超市相距
B.娟娟同学去超市途中的速度是
C.娟娟同学在超市逗留了
D.娟娟同学从超市返回家中比从家里去超市的速度快
6.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
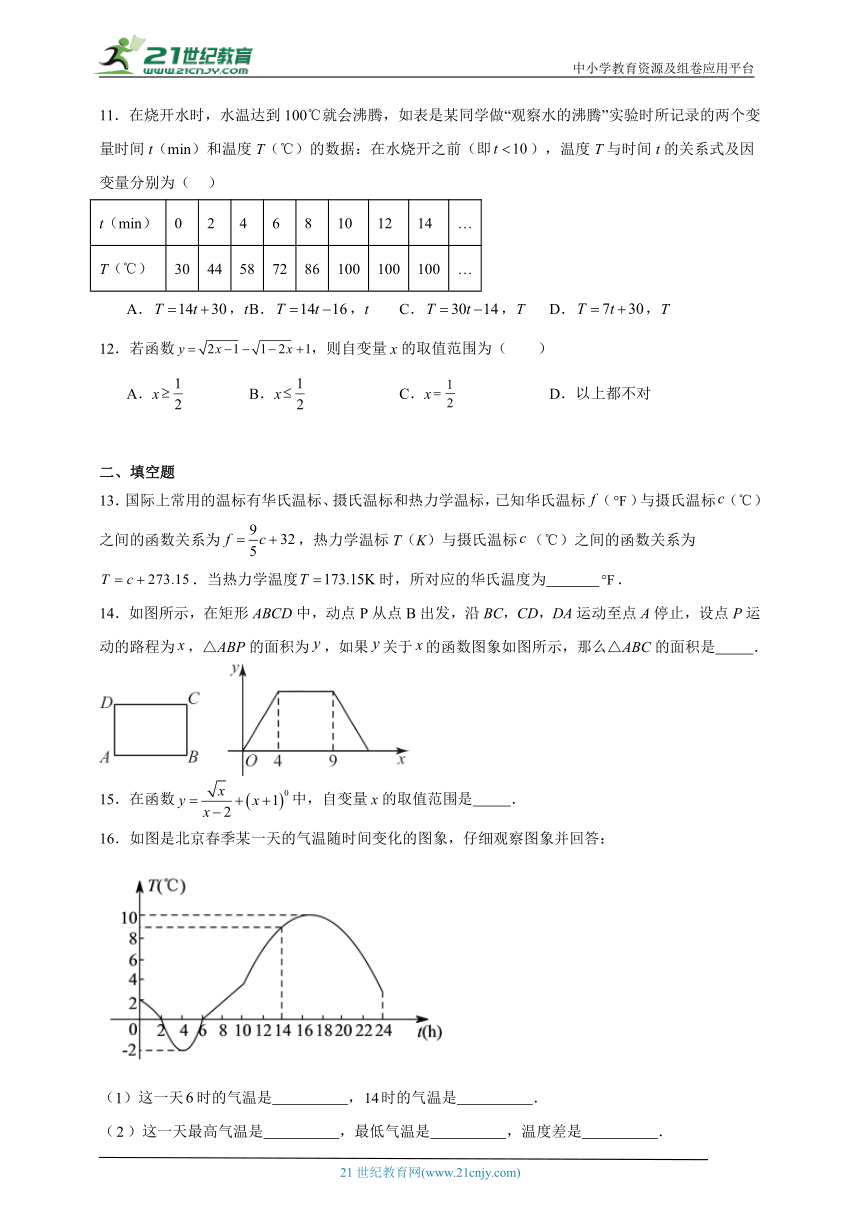
7.下列曲线中不能表示 y是 x的函数的是( )
A. B. C. D.
8.周末小海约小亮一起去新华书店,如右图是小海先到小亮家,然后他们一起去新华书店的示意图.下面的描述与图意不相符的是( )
A.小海从家到新华书店一共经过24分钟 B.小海从家到书店的平均速度是米/分钟
C.小海家到书店的距离是1000米 D.小海家与小亮家的距离是600米
9.在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
m 1 2 3 4
v 0.01 2.9 8.03 15.1
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m-1 B.v=m2-1 C.v=3m-3 D.v=m+1
10.函数y中自变量x的取值范围是( )
A.x≥1 B.x>2 C.x≥1且x≠2 D.x≠2
11.在烧开水时,水温达到100℃就会沸腾,如表是某同学做“观察水的沸腾”实验时所记录的两个变量时间t(min)和温度T(℃)的数据:在水烧开之前(即),温度T与时间t的关系式及因变量分别为( )
t(min) 0 2 4 6 8 10 12 14 …
T(℃) 30 44 58 72 86 100 100 100 …
A.,t B.,t C.,T D.,T
12.若函数,则自变量x的取值范围为( )
A.x B.x C.x D.以上都不对
二、填空题
13.国际上常用的温标有华氏温标、摄氏温标和热力学温标,已知华氏温标()与摄氏温标(℃)之间的函数关系为,热力学温标T(K)与摄氏温标(℃)之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
14.如图所示,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为,△ABP的面积为,如果关于的函数图象如图所示,那么△ABC的面积是 .
15.在函数中,自变量x的取值范围是 .
16.如图是北京春季某一天的气温随时间变化的图象,仔细观察图象并回答:
()这一天时的气温是 ,时的气温是 .
()这一天最高气温是 ,最低气温是 ,温度差是 .
17.2024年3月14日森林学校举行了以为主题的数学节,小兔和小龟进行了新型的“龟兔赛跑”比赛,它们在校园的型跑道(图1)进行赛跑,小兔以A为起点,沿着的线路到达终点D,小龟以B为起点,沿着的线路到达终点C.小龟提前出发,小兔和小龟在经过线路中的大树E时都休息了2分钟,再以原速度继续比赛,最终小兔和小龟同时到达各自的终点.设小兔所跑的时间为x分钟(),小龟所跑的路程与小兔所跑的路程差为y米,,图2是y与x的函数关系图象,则下列说法正确的是 (填写正确的序号).
①小龟跑了500米后小兔出发;
②当时,小龟到达大树E开始休息;
③小兔的速度为100米/分钟,大树E距离小兔的起点A800米.
三、解答题
18.当蜡烛被点燃后,蜡烛的长度会随燃烧时间发生变化.研究表明,在蜡烛可燃烧长度内,蜡烛剩余的长度y()与燃烧时间x()之间为一次函数关系,某实验小组将得到的数据绘制成如下表格.
燃烧时间x() 0 1 2 3
剩余长度y() 20 17 14 11
(1)求蜡烛剩余长度y()与燃烧时间x()之间的函数表达式,并写出自变量的取值范围;
(2)当蜡烛燃烧5后,求蜡烛剩余的长度.
19.如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)试写出点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
20.如图1,长方形中,,点从B出发,沿方向运动,经过D,C,到B停止,点的速度为每秒,秒时点改变速度,变为每秒,图2是点出发t秒后的面积与t(秒)的关系图象.
(1)直接写出 , , ;
(2)设点离开点B的路程为,求出路程与运动时间t(秒)的关系式;
(3)直接写出,当点出发多少秒后,.
21.完成以下问题:
(1)某人持续以a(m/min)的速度在t(min)内跑了s(m),其中常量是____,变量是____.
(2)在t(min)内,不同的人以不同的速度a(m/min)跑了s(m),其中常量是___,变量是____.
(3)s(m)的路程,不同的人以不同的速度a(m/min)各需跑t(min),其中常量是____,变量是____.
(4)根据以上叙述,写一句关于常量与变量的结论:__________.
22.某厂现有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件.已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需甲种原料4kg,乙种原料10kg,可获利润1200元.现设生产A种产品x件.
(1)请用x的式子分别表示生产A,B两种产品共需要_______kg甲种原料,_____kg乙种原料.
(2)设生产A,B两种产品获得的总利润是y(元),试写出y与x之间的表达式.
23.“人间四月芳菲尽,山寺桃花始盛开”,是说因为气温随地势的上升而降低这一特点,才造成了山上、山下的桃花花期早迟不一这种地理现象.下面是小明对某地某一时刻距离地面的高度 与温度 测量得到的表格.
距离地面高度(千米)
温度(℃)
请回答下列问题:
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)与之间的关系式是 .
(3)你能估计温度为时,距离地面的高度是多少吗
24.写出下列各个过程中的变量与常量:
(1)我国第一颗人造地球卫星绕地球1周需内卫星绕地球的周数为N,;
(2)长方形的长为2,它的面积S与宽a的关系式为.
《第二十章函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B B D C B B B C
题号 11 12
答案 D C
1.D
【分析】根据图象信息,逐项判断即可.
【详解】解:A、王华在体育场锻炼的时间为:30-15=15(min),在文具店退留的时间为:65-45=20(min),所以原结论错误,故本选项不合题意;
B、体育场与文具店的距离为2.5-1.5=1(km),所以原结论错误,故本选项不合题意;
C、王华的跑步速度是:2.5÷15=( km/min),所以原结论错误,故本选项不合题意;
D、王华从体育场步行去文具店的速度为:1÷(45-30)=( km/min),
从文具店步行回家的速度为:1.5÷(100-65)=( km/min),
∵=>,
∴王华从体育场步行去文具店的速度比从文具店步行回家的速度快,
故原结论正确,故本选项符合题意.
故选:D.
【点睛】本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
2.C
【分析】根据被开方式是非负数列式求解即可.
【详解】解:由题意,得
6﹣x≥0,
解得x≤6,
故选C.
【点睛】本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:①当函数解析式是整式时,字母可取全体实数;②当函数解析式是分式时,考虑分式的分母不能为0;③当函数解析式是二次根式时,被开方数为非负数.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
3.B
【详解】由题意得:y=3a,
此问题中a、y都是变量,3是常量,或a,y都是常量,则③④,
故选B.
4.B
【分析】根据题意,可知图象分两段,第一段为常数函数,第二段时,x每增加1,y随之增加1,据此判断即可.
【详解】解:∵路程2km内运费5元,
∴2km内运费不变,为5元,
当时,每增加1千米,运费就增加1元,
故选:B.
【点睛】本题考查了用函数图象表示变量之间的关系,准确理解题意是解题的关键.
5.D
【分析】仔细观察图象的横纵坐标所表示的量的意义,从而进行判断.
【详解】A、娟娟同学与超市相距3000m,正确;
B、娟娟同学去超市途中的速度是=300m/min,正确;
C、娟娟同学在超市逗留了40-10=30min,正确;
D、娟娟同学从超市返回家比从家里去超市的速度慢,错误;
故选:D.
【点睛】此题考查函数的图象,能够仔细读图并从中整理出进一步解题的有关信息是解题的关键,难度不大.
6.C
【分析】根据图像,结合行程问题的数量关系逐项分析可得出答案.
【详解】从图象来看,小明在第40分钟时开始休息,第60分钟时结束休息,故休息用了20分钟,A正确;
小明休息前爬山的平均速度为:(米/分),B正确;
小明在上述过程中所走的路程为3800米,C错误;
小明休息前爬山的平均速度为:70米/分,大于休息后爬山的平均速度:米/分,D正确.
故选:C.
考点:函数的图象、行程问题.
7.B
【分析】本题考查了函数的定义,掌握函数的定义是解题关键.
根据函数的定义,对于x的每一个确定的值,y都有唯一的值与其对应,确定正确的选项.
【详解】解:选项ACD中,对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A、C、D均不符合题意;
B、对于自变量x的值,因变量y不是唯一的值与它对应,所以y是x的函数,故B不符合题意;
故选:B.
8.B
【分析】本题考查的是从图象中获取信息,根据图象的含义结合速度,时间,路程的关系逐一判断即可.
【详解】解:由图象可知,小海从家到新华书店一共经过分钟,故A不符合题意;
小海从家到书店的平均速度是(米/分钟),故B符合题意;
小海家到书店的距离是米,故C不符合题意;
小海家与小亮家的距离是600米,故D不符合题意;
故选:B.
9.B
【分析】一般情况下是把最大的一对数据代入函数关系式后通过比较得出最接近的关系式.
【详解】解:当m=4时,
A、v=2m-2=6;B、v=m2-1=15;
C、v=3m-3=9;D、v=m+1=5.
故选B.
【点睛】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量;解题关键是分别把数据代入下列函数,通过比较找到最符合的函数关系式.
10.C
【分析】本题考查代数式有意义的条件:(1)分母不为0;(2)二次被开方数大于等于0. 据此列出不等式组再求解即可.
【详解】运用分析中的两个条件,可列不等式组:
,解得:x≥1且x≠2.
故选:C.
【点睛】明确分析中两个条件的依据,是掌握代数式有意义的条件的关键.
11.D
【分析】由表知开始时温度为30℃,再每增加2分钟,温度增加14℃,即每增加1分钟,温度增加7℃,可得温度T与时间t的关系式.
【详解】解:∵开始时温度为30℃,每增加1分钟,温度增加7℃,
∴温度T与时间t的关系式为:,
因变量为T,
故选:D.
【点睛】本题考查了求函数的关系式,关键是得出开始时温度为30℃,每增加1分钟,温度增加7℃.
12.C
【分析】要使式子有意义,被开方数要大于等于0,列不等式组求解.
【详解】解:要使二次根式有意义,
则,
解得,
故选:C.
【点睛】本题主要考查二次根式有意义的条件,解题的关键是掌握被开方数为非负数.
13.
【分析】本题考查了方程的应用和函数关系式,解题关键是根据题意代入求出c,再代入c,通过解方程求解.
【详解】解:把代入得,
,
解得,
把代入得,
,
故答案为:.
14.10
【详解】解:根据题意可得:AB=5,BC=4,
∴△ABC的面积是:×4×5=10.
故答案为10
15.且
【分析】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.根据被开方数大于等于0,分母不等于0,零指数幂的底数不等于0列式计算即可得解.
【详解】解:由题意得,且,,
解得且,,
所以,且,
故答案为:且.
16. ℃ ℃ ℃ ℃ ℃
【详解】试题分析:(1)观察函数的图象,找出6时,14时的气温即可;
(2)在函数的图象上找出最高气温、最低气温,通过计算求得温差即可.
试题解析:(1)由图可知这天的6时气温为0℃,14时气温为9℃,
故答案为0℃,9℃;
(2)从图中看出最高气温是10℃,最低气温是-2℃,温差为:12-(-2)=14℃,
故答案为10℃,-2℃,14℃.
【点睛】本题考查了函数的图象,本题比较简单,关键是能读懂函数图象,从函数图象中获得有关信息.
17.①③/③①
【分析】本题主要考查了从函数图象获取信息,根据当时,,即可判断①;在第7分钟时,,则在兔子出发7分钟后兔子和乌龟的路程相同,继续运动到第8秒后,兔子所走的路程比乌龟大,在第8分钟到第10分钟,兔子和乌龟的路程差值减小,则此过程兔子在休息,乌龟在继续运动,据此可判断②;第8分到第10分钟,只有乌龟在比赛;第10分钟到第12分钟,每分钟内兔子和乌龟的路程差为米,而在前 7分钟,每分钟的路程差为米,据此可得第10分钟到第12分钟内乌龟休息,兔子运动,据此求出兔子的速度,进而求出兔子与大树E的距离,即可判断③.
【详解】解:①当时,.
∵小龟所跑的路程与小兔所跑的路程差为y米,,,
∴小龟跑了500米后小兔出发.故①正确;
②在第7分钟时,,则在兔子出发7分钟后兔子和乌龟的路程相同,继续运动到第8秒后,兔子所走的路程比乌龟大,在第8分钟到第10分钟,兔子和乌龟的路程差值减小,因此此过程兔子在休息,乌龟在继续运动,故②错误;
③第8分到第10分钟,只有乌龟在比赛;第10分钟到第12分钟,每分钟内兔子和乌龟的路程差为米,而在前 7分钟,每分钟的路程差为米,而在两只动物运动过程中速度不变,那么在同时运动过程中二者每分钟的路程差是不变的,
∴第10分钟到第12分钟内乌龟休息,兔子运动,
∴兔子的运动速度为每分钟100米,
∴兔子与大树E的距离为米故③正确.
故答案为:①③.
18.(1)函数表达式为();
(2)当蜡烛燃烧5后,蜡烛剩余长度为5.
【分析】本题考查用数学式子表示函数解析式、实际问题中函数自变量的取值范围、以及函数值,解题的关键在于根据表中数量关系得出函数解析式.
(1)根据表格中自变量和因变量的等量关系,列出函数解析式,再根据实际问题中蜡烛最长和最短的情况,即可得到自变量的取值范围;
(2)根据题意得到自变量为,再根据函数解析式求其函数值,即可解题.
【详解】(1)解:观察表中数据可得蜡烛初始长度为20,每燃烧1蜡烛减少3,
函数表达式为.
当蜡烛燃烧完,即时,,
自变量的取值范围为.
(2)解:当时,.
答:当蜡烛燃烧5后,蜡烛剩余长度为5.
19.(1)
(2)3秒或秒或11秒或13秒
【分析】(1)因为A以每秒2厘米的速度自左向右运动,所以此题要分两种情况讨论:当点A在点B的左侧时,圆心距等于11减去点A所走的路程;当点A在点B的右侧时,圆心距等于点A走的路程减去11;
(2)根据两圆相切时,两圆的半径与圆心距的关系,分4种情况讨论,即可求解.
【详解】(1)解:根据题意得∶当时,点A在点B的左侧,此时函数表达式为;
当时,点A在点B的右侧,此时函数表达式为.
所以点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式为;
(2)解:两圆相切可分为如下四种情况:
①当两圆第一次外切,由题意得,
解得;
②当两圆第一次内切,由题意得,
解得;
③当两圆第二次内切,由题意得,
解得;
④当两圆第二次外切,由题意得,
解得.
所以,点A出发后3秒或秒或11秒或13秒两圆相切.
【点睛】本题考查了圆与圆的位置关系,解题的关键是能够将移动的过程中两圆的位置关系全部考虑到,难度不大.
20.(1)5;;4
(2)
(3)或
【分析】本题考查动点问题的函数图象,一元一次方程的实际应用,从函数图象获取信息是解题的关键.
(1)根据a秒时的面积可求a的值,由6.5秒时,点P与点D重合,利用路程速度时间,即可求出k的值,由时间路程速度即可求出b的值;
(2)分为点P速度为每秒和点P速度为每秒,两种情况由路程速度时间,列出关系式即可;
(3)分为点P在上和点P在上,两种情况讨论即可.
【详解】(1)解:根据图象可得:a秒时的面积为12,即,
,
,
;
6.5秒时,点P与点D重合,
;
点P从点D运动到点B的速度为每秒,
,
长方形中,,
;
(2)解:点P速度为每秒时:;
点P速度为每秒时:;
综上,;
(3)解:点P在上时,
当点P加速前:
,
(舍去,不符合题意),
当点P加速后:
,
;
当点P运动到点C时,所需时间为:(秒),
点P在上时,,
,
,
综上,当点出发或时,.
21. a t,s t a,s s a,t 在不同条件下,常量与变量是相对的
【详解】试题分析:根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可直接得到答案.
试题解析:(1)某人持续以a米/分钟的速度t分钟内跑了s米,其中常量是a,变量是t,s;
(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是t,变量是a,s;
(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是s,变量是a,t;
(4)根据以上叙述,写一句关于常量与变量的结论:在不同条件下,常量与变量是相对的.
22.(1)200+5x,500-7x;(2)y=60000-500x
【分析】(1)由A、B一共生产50件可得,B生产(50-x)件,再根据生产A、B两种产品各需原料即可得出结论;
(2)由A一件可获利700元,生产一件B种产品获利1200元可得关系式.
【详解】(1)因为A、B一共生产50件,现设生产A种产品x件,
所以B产品生产(50-x)件,
又因为已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg;生产一件B种产品,需甲种原料4kg,乙种原料10kg,
所以共需要9x+4(50-x)=(200+5x)kg甲种原料,3x+10(50-x)=(500-7x)kg乙种原料;
(2)因为A一件可获利700元,生产一件B种产品获利1200元,
所以y=700x+1200(50-x)=60000-500x.
【点睛】考查了列一次函数,解题关键抓住题中的等量关系进行解题.
23.(1)上表反映了温度和距离地面高度之间的关系,距离地面高度是自变量,温度是因变量
(2)
(3)温度为时,距离地面的高度是千米
【分析】本题考查函数的定义,表格表示函数关系,求函数值;
(1)根据函数的定义即可求解;
(2)由表格可知当高度每上升时,温度下降,然后计算即可;
(3)将代入解析式,即可求解.
【详解】(1)解:上表反映了温度和距离地面高度之间的关系,距离地面高度是自变量,温度是因变量.
(2)根据表格数据知当高度每上升时,温度下降,
∴;
(3)将代入 ,
可得:,
解得 ,
答:温度为时,距离地面的高度是千米.
24.(1)N和t是变量,114是常量
(2)S和a是变量,2是常量
【分析】本题主要考查了常量与变量,熟练掌握常量与变量的定义是解题的关键.
(1)根据在这一变化过程中,是保持不变的量;和是可以取不同数值的量分析判断即可得解;
(2)根据在这一变化过程中,是保持不变的量;和是可以取不同数值的量分析判断即可得解.
【详解】(1)解:和是变量,是常量;
(2)解:和是变量,是常量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
第二十章函数
学校:___________姓名:___________班级:___________考号:___________
一、单选题
1.王华积极响应《体质管理通知》中的规定:每天坚持校外1小时体育活动时间.已知王华家、体育场、文具店在同一直线上.下图所反映的过程是:王华从家跑步去体育场,锻炼了一阵后,又走到文具店买笔,然后步行回家.图中x表示时间,y表示王华离家的距离.下列说法正确的是( )
A.王华在体育场锻炼的时间和在文具店退留的时间相同
B.体育场与文具店的距离为
C.王华的跑步速度是
D.王华从体育场步行去文具店的速度比从文具店步行回家的速度快
2.使函数y=有意义的自变量x的取值范围是( )
A.x≥6 B.x≥0 C.x≤6 D.x≤0
3.笔记本每本a元,买3本笔记本共支出y元,在这个问题中:
①a是常量时,y是变量;
②a是变量时,y是常量;
③a是变量时,y也是变量;
④a,y可以都是常量或都是变量.
上述判断正确的有( )
A.1个 B.2个 C.3个 D.4个
4.某市运货的摩托车的运输价格为:路程2km内运费5元;超过2km后,每1km增加运费1元,那么运费y(单位:元)与路程x(单位:km)的函数图象是( )
A. B. C. D.
5.娟娟同学上午从家出发,骑车去一家超市购物,然后从这家超市返回家中,娟娟同学离家的路程和所经过的时间之间的函数图形如图所示,则下列说法不正确的是( )
A.娟娟同学与超市相距
B.娟娟同学去超市途中的速度是
C.娟娟同学在超市逗留了
D.娟娟同学从超市返回家中比从家里去超市的速度快
6.今年“五一”节,小明外出爬山,他从山脚爬到山顶的过程中,中途休息了一段时间.设他从山脚出发后所用的时间为t(分钟),所走的路程为s(米),s与t之间的函数关系如图所示,下列说法错误的是( )
A.小明中途休息用了20分钟
B.小明休息前爬山的平均速度为每分钟70米
C.小明在上述过程中所走的路程为6600米
D.小明休息前爬山的平均速度大于休息后爬山的平均速度
7.下列曲线中不能表示 y是 x的函数的是( )
A. B. C. D.
8.周末小海约小亮一起去新华书店,如右图是小海先到小亮家,然后他们一起去新华书店的示意图.下面的描述与图意不相符的是( )
A.小海从家到新华书店一共经过24分钟 B.小海从家到书店的平均速度是米/分钟
C.小海家到书店的距离是1000米 D.小海家与小亮家的距离是600米
9.在某次试验中,测得两个变量m和v之间的4组对应数据如下表:
m 1 2 3 4
v 0.01 2.9 8.03 15.1
则m与v之间的关系最接近于下列各关系式中的( )
A.v=2m-1 B.v=m2-1 C.v=3m-3 D.v=m+1
10.函数y中自变量x的取值范围是( )
A.x≥1 B.x>2 C.x≥1且x≠2 D.x≠2
11.在烧开水时,水温达到100℃就会沸腾,如表是某同学做“观察水的沸腾”实验时所记录的两个变量时间t(min)和温度T(℃)的数据:在水烧开之前(即),温度T与时间t的关系式及因变量分别为( )
t(min) 0 2 4 6 8 10 12 14 …
T(℃) 30 44 58 72 86 100 100 100 …
A.,t B.,t C.,T D.,T
12.若函数,则自变量x的取值范围为( )
A.x B.x C.x D.以上都不对
二、填空题
13.国际上常用的温标有华氏温标、摄氏温标和热力学温标,已知华氏温标()与摄氏温标(℃)之间的函数关系为,热力学温标T(K)与摄氏温标(℃)之间的函数关系为.当热力学温度时,所对应的华氏温度为 .
14.如图所示,在矩形ABCD中,动点P从点B出发,沿BC,CD,DA运动至点A停止,设点P运动的路程为,△ABP的面积为,如果关于的函数图象如图所示,那么△ABC的面积是 .
15.在函数中,自变量x的取值范围是 .
16.如图是北京春季某一天的气温随时间变化的图象,仔细观察图象并回答:
()这一天时的气温是 ,时的气温是 .
()这一天最高气温是 ,最低气温是 ,温度差是 .
17.2024年3月14日森林学校举行了以为主题的数学节,小兔和小龟进行了新型的“龟兔赛跑”比赛,它们在校园的型跑道(图1)进行赛跑,小兔以A为起点,沿着的线路到达终点D,小龟以B为起点,沿着的线路到达终点C.小龟提前出发,小兔和小龟在经过线路中的大树E时都休息了2分钟,再以原速度继续比赛,最终小兔和小龟同时到达各自的终点.设小兔所跑的时间为x分钟(),小龟所跑的路程与小兔所跑的路程差为y米,,图2是y与x的函数关系图象,则下列说法正确的是 (填写正确的序号).
①小龟跑了500米后小兔出发;
②当时,小龟到达大树E开始休息;
③小兔的速度为100米/分钟,大树E距离小兔的起点A800米.
三、解答题
18.当蜡烛被点燃后,蜡烛的长度会随燃烧时间发生变化.研究表明,在蜡烛可燃烧长度内,蜡烛剩余的长度y()与燃烧时间x()之间为一次函数关系,某实验小组将得到的数据绘制成如下表格.
燃烧时间x() 0 1 2 3
剩余长度y() 20 17 14 11
(1)求蜡烛剩余长度y()与燃烧时间x()之间的函数表达式,并写出自变量的取值范围;
(2)当蜡烛燃烧5后,求蜡烛剩余的长度.
19.如图,点A,B在直线MN上,AB=11厘米,⊙A,⊙B的半径均为1厘米.⊙A以每秒2厘米的速度自左向右运动,与此同时,⊙B的半径也不断增大,其半径r(厘米)与时间t(秒)之间的关系式为r=1+t(t≥0).
(1)试写出点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式;
(2)问点A出发后多少秒两圆相切?
20.如图1,长方形中,,点从B出发,沿方向运动,经过D,C,到B停止,点的速度为每秒,秒时点改变速度,变为每秒,图2是点出发t秒后的面积与t(秒)的关系图象.
(1)直接写出 , , ;
(2)设点离开点B的路程为,求出路程与运动时间t(秒)的关系式;
(3)直接写出,当点出发多少秒后,.
21.完成以下问题:
(1)某人持续以a(m/min)的速度在t(min)内跑了s(m),其中常量是____,变量是____.
(2)在t(min)内,不同的人以不同的速度a(m/min)跑了s(m),其中常量是___,变量是____.
(3)s(m)的路程,不同的人以不同的速度a(m/min)各需跑t(min),其中常量是____,变量是____.
(4)根据以上叙述,写一句关于常量与变量的结论:__________.
22.某厂现有甲种原料360kg,乙种原料290kg,计划用这两种原料生产A、B两种产品共50件.已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg,可获利润700元;生产一件B种产品,需甲种原料4kg,乙种原料10kg,可获利润1200元.现设生产A种产品x件.
(1)请用x的式子分别表示生产A,B两种产品共需要_______kg甲种原料,_____kg乙种原料.
(2)设生产A,B两种产品获得的总利润是y(元),试写出y与x之间的表达式.
23.“人间四月芳菲尽,山寺桃花始盛开”,是说因为气温随地势的上升而降低这一特点,才造成了山上、山下的桃花花期早迟不一这种地理现象.下面是小明对某地某一时刻距离地面的高度 与温度 测量得到的表格.
距离地面高度(千米)
温度(℃)
请回答下列问题:
(1)上表反映了哪两个变量之间的关系 哪个是自变量 哪个是因变量
(2)与之间的关系式是 .
(3)你能估计温度为时,距离地面的高度是多少吗
24.写出下列各个过程中的变量与常量:
(1)我国第一颗人造地球卫星绕地球1周需内卫星绕地球的周数为N,;
(2)长方形的长为2,它的面积S与宽a的关系式为.
《第二十章函数》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 D C B B D C B B B C
题号 11 12
答案 D C
1.D
【分析】根据图象信息,逐项判断即可.
【详解】解:A、王华在体育场锻炼的时间为:30-15=15(min),在文具店退留的时间为:65-45=20(min),所以原结论错误,故本选项不合题意;
B、体育场与文具店的距离为2.5-1.5=1(km),所以原结论错误,故本选项不合题意;
C、王华的跑步速度是:2.5÷15=( km/min),所以原结论错误,故本选项不合题意;
D、王华从体育场步行去文具店的速度为:1÷(45-30)=( km/min),
从文具店步行回家的速度为:1.5÷(100-65)=( km/min),
∵=>,
∴王华从体育场步行去文具店的速度比从文具店步行回家的速度快,
故原结论正确,故本选项符合题意.
故选:D.
【点睛】本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.本题考查了函数图象,正确理解函数图象横纵坐标表示的意义,理解问题的过程,就能够通过图象得到函数问题的相应解决.需注意计算单位的统一.
2.C
【分析】根据被开方式是非负数列式求解即可.
【详解】解:由题意,得
6﹣x≥0,
解得x≤6,
故选C.
【点睛】本题考查了函数自变量的取值范围,函数有意义时字母的取值范围一般从几个方面考虑:①当函数解析式是整式时,字母可取全体实数;②当函数解析式是分式时,考虑分式的分母不能为0;③当函数解析式是二次根式时,被开方数为非负数.④对于实际问题中的函数关系式,自变量的取值除必须使表达式有意义外,还要保证实际问题有意义.
3.B
【详解】由题意得:y=3a,
此问题中a、y都是变量,3是常量,或a,y都是常量,则③④,
故选B.
4.B
【分析】根据题意,可知图象分两段,第一段为常数函数,第二段时,x每增加1,y随之增加1,据此判断即可.
【详解】解:∵路程2km内运费5元,
∴2km内运费不变,为5元,
当时,每增加1千米,运费就增加1元,
故选:B.
【点睛】本题考查了用函数图象表示变量之间的关系,准确理解题意是解题的关键.
5.D
【分析】仔细观察图象的横纵坐标所表示的量的意义,从而进行判断.
【详解】A、娟娟同学与超市相距3000m,正确;
B、娟娟同学去超市途中的速度是=300m/min,正确;
C、娟娟同学在超市逗留了40-10=30min,正确;
D、娟娟同学从超市返回家比从家里去超市的速度慢,错误;
故选:D.
【点睛】此题考查函数的图象,能够仔细读图并从中整理出进一步解题的有关信息是解题的关键,难度不大.
6.C
【分析】根据图像,结合行程问题的数量关系逐项分析可得出答案.
【详解】从图象来看,小明在第40分钟时开始休息,第60分钟时结束休息,故休息用了20分钟,A正确;
小明休息前爬山的平均速度为:(米/分),B正确;
小明在上述过程中所走的路程为3800米,C错误;
小明休息前爬山的平均速度为:70米/分,大于休息后爬山的平均速度:米/分,D正确.
故选:C.
考点:函数的图象、行程问题.
7.B
【分析】本题考查了函数的定义,掌握函数的定义是解题关键.
根据函数的定义,对于x的每一个确定的值,y都有唯一的值与其对应,确定正确的选项.
【详解】解:选项ACD中,对于自变量x的每一个值,因变量y都有唯一的值与它对应,所以y是x的函数,故A、C、D均不符合题意;
B、对于自变量x的值,因变量y不是唯一的值与它对应,所以y是x的函数,故B不符合题意;
故选:B.
8.B
【分析】本题考查的是从图象中获取信息,根据图象的含义结合速度,时间,路程的关系逐一判断即可.
【详解】解:由图象可知,小海从家到新华书店一共经过分钟,故A不符合题意;
小海从家到书店的平均速度是(米/分钟),故B符合题意;
小海家到书店的距离是米,故C不符合题意;
小海家与小亮家的距离是600米,故D不符合题意;
故选:B.
9.B
【分析】一般情况下是把最大的一对数据代入函数关系式后通过比较得出最接近的关系式.
【详解】解:当m=4时,
A、v=2m-2=6;B、v=m2-1=15;
C、v=3m-3=9;D、v=m+1=5.
故选B.
【点睛】主要考查了函数的定义.函数的定义:在一个变化过程中,有两个变量x,y,对于x的每一个取值,y都有唯一确定的值与之对应,则y是x的函数,x叫自变量;解题关键是分别把数据代入下列函数,通过比较找到最符合的函数关系式.
10.C
【分析】本题考查代数式有意义的条件:(1)分母不为0;(2)二次被开方数大于等于0. 据此列出不等式组再求解即可.
【详解】运用分析中的两个条件,可列不等式组:
,解得:x≥1且x≠2.
故选:C.
【点睛】明确分析中两个条件的依据,是掌握代数式有意义的条件的关键.
11.D
【分析】由表知开始时温度为30℃,再每增加2分钟,温度增加14℃,即每增加1分钟,温度增加7℃,可得温度T与时间t的关系式.
【详解】解:∵开始时温度为30℃,每增加1分钟,温度增加7℃,
∴温度T与时间t的关系式为:,
因变量为T,
故选:D.
【点睛】本题考查了求函数的关系式,关键是得出开始时温度为30℃,每增加1分钟,温度增加7℃.
12.C
【分析】要使式子有意义,被开方数要大于等于0,列不等式组求解.
【详解】解:要使二次根式有意义,
则,
解得,
故选:C.
【点睛】本题主要考查二次根式有意义的条件,解题的关键是掌握被开方数为非负数.
13.
【分析】本题考查了方程的应用和函数关系式,解题关键是根据题意代入求出c,再代入c,通过解方程求解.
【详解】解:把代入得,
,
解得,
把代入得,
,
故答案为:.
14.10
【详解】解:根据题意可得:AB=5,BC=4,
∴△ABC的面积是:×4×5=10.
故答案为10
15.且
【分析】本题考查了函数自变量的范围,一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.根据被开方数大于等于0,分母不等于0,零指数幂的底数不等于0列式计算即可得解.
【详解】解:由题意得,且,,
解得且,,
所以,且,
故答案为:且.
16. ℃ ℃ ℃ ℃ ℃
【详解】试题分析:(1)观察函数的图象,找出6时,14时的气温即可;
(2)在函数的图象上找出最高气温、最低气温,通过计算求得温差即可.
试题解析:(1)由图可知这天的6时气温为0℃,14时气温为9℃,
故答案为0℃,9℃;
(2)从图中看出最高气温是10℃,最低气温是-2℃,温差为:12-(-2)=14℃,
故答案为10℃,-2℃,14℃.
【点睛】本题考查了函数的图象,本题比较简单,关键是能读懂函数图象,从函数图象中获得有关信息.
17.①③/③①
【分析】本题主要考查了从函数图象获取信息,根据当时,,即可判断①;在第7分钟时,,则在兔子出发7分钟后兔子和乌龟的路程相同,继续运动到第8秒后,兔子所走的路程比乌龟大,在第8分钟到第10分钟,兔子和乌龟的路程差值减小,则此过程兔子在休息,乌龟在继续运动,据此可判断②;第8分到第10分钟,只有乌龟在比赛;第10分钟到第12分钟,每分钟内兔子和乌龟的路程差为米,而在前 7分钟,每分钟的路程差为米,据此可得第10分钟到第12分钟内乌龟休息,兔子运动,据此求出兔子的速度,进而求出兔子与大树E的距离,即可判断③.
【详解】解:①当时,.
∵小龟所跑的路程与小兔所跑的路程差为y米,,,
∴小龟跑了500米后小兔出发.故①正确;
②在第7分钟时,,则在兔子出发7分钟后兔子和乌龟的路程相同,继续运动到第8秒后,兔子所走的路程比乌龟大,在第8分钟到第10分钟,兔子和乌龟的路程差值减小,因此此过程兔子在休息,乌龟在继续运动,故②错误;
③第8分到第10分钟,只有乌龟在比赛;第10分钟到第12分钟,每分钟内兔子和乌龟的路程差为米,而在前 7分钟,每分钟的路程差为米,而在两只动物运动过程中速度不变,那么在同时运动过程中二者每分钟的路程差是不变的,
∴第10分钟到第12分钟内乌龟休息,兔子运动,
∴兔子的运动速度为每分钟100米,
∴兔子与大树E的距离为米故③正确.
故答案为:①③.
18.(1)函数表达式为();
(2)当蜡烛燃烧5后,蜡烛剩余长度为5.
【分析】本题考查用数学式子表示函数解析式、实际问题中函数自变量的取值范围、以及函数值,解题的关键在于根据表中数量关系得出函数解析式.
(1)根据表格中自变量和因变量的等量关系,列出函数解析式,再根据实际问题中蜡烛最长和最短的情况,即可得到自变量的取值范围;
(2)根据题意得到自变量为,再根据函数解析式求其函数值,即可解题.
【详解】(1)解:观察表中数据可得蜡烛初始长度为20,每燃烧1蜡烛减少3,
函数表达式为.
当蜡烛燃烧完,即时,,
自变量的取值范围为.
(2)解:当时,.
答:当蜡烛燃烧5后,蜡烛剩余长度为5.
19.(1)
(2)3秒或秒或11秒或13秒
【分析】(1)因为A以每秒2厘米的速度自左向右运动,所以此题要分两种情况讨论:当点A在点B的左侧时,圆心距等于11减去点A所走的路程;当点A在点B的右侧时,圆心距等于点A走的路程减去11;
(2)根据两圆相切时,两圆的半径与圆心距的关系,分4种情况讨论,即可求解.
【详解】(1)解:根据题意得∶当时,点A在点B的左侧,此时函数表达式为;
当时,点A在点B的右侧,此时函数表达式为.
所以点A,B之间的距离d(厘米)与时间t(秒)之间的函数表达式为;
(2)解:两圆相切可分为如下四种情况:
①当两圆第一次外切,由题意得,
解得;
②当两圆第一次内切,由题意得,
解得;
③当两圆第二次内切,由题意得,
解得;
④当两圆第二次外切,由题意得,
解得.
所以,点A出发后3秒或秒或11秒或13秒两圆相切.
【点睛】本题考查了圆与圆的位置关系,解题的关键是能够将移动的过程中两圆的位置关系全部考虑到,难度不大.
20.(1)5;;4
(2)
(3)或
【分析】本题考查动点问题的函数图象,一元一次方程的实际应用,从函数图象获取信息是解题的关键.
(1)根据a秒时的面积可求a的值,由6.5秒时,点P与点D重合,利用路程速度时间,即可求出k的值,由时间路程速度即可求出b的值;
(2)分为点P速度为每秒和点P速度为每秒,两种情况由路程速度时间,列出关系式即可;
(3)分为点P在上和点P在上,两种情况讨论即可.
【详解】(1)解:根据图象可得:a秒时的面积为12,即,
,
,
;
6.5秒时,点P与点D重合,
;
点P从点D运动到点B的速度为每秒,
,
长方形中,,
;
(2)解:点P速度为每秒时:;
点P速度为每秒时:;
综上,;
(3)解:点P在上时,
当点P加速前:
,
(舍去,不符合题意),
当点P加速后:
,
;
当点P运动到点C时,所需时间为:(秒),
点P在上时,,
,
,
综上,当点出发或时,.
21. a t,s t a,s s a,t 在不同条件下,常量与变量是相对的
【详解】试题分析:根据变量和常量的定义:在一个变化的过程中,数值发生变化的量称为变量;数值始终不变的量称为常量可直接得到答案.
试题解析:(1)某人持续以a米/分钟的速度t分钟内跑了s米,其中常量是a,变量是t,s;
(2)在t分钟内,不同的人以不同的速度a米/分钟跑了s米,其中常量是t,变量是a,s;
(3)s米的路程不同的人以不同的速度a米/分钟各需跑t分钟,其中常量是s,变量是a,t;
(4)根据以上叙述,写一句关于常量与变量的结论:在不同条件下,常量与变量是相对的.
22.(1)200+5x,500-7x;(2)y=60000-500x
【分析】(1)由A、B一共生产50件可得,B生产(50-x)件,再根据生产A、B两种产品各需原料即可得出结论;
(2)由A一件可获利700元,生产一件B种产品获利1200元可得关系式.
【详解】(1)因为A、B一共生产50件,现设生产A种产品x件,
所以B产品生产(50-x)件,
又因为已知生产一件A种产品,需用甲种原料9kg,乙种原料3kg;生产一件B种产品,需甲种原料4kg,乙种原料10kg,
所以共需要9x+4(50-x)=(200+5x)kg甲种原料,3x+10(50-x)=(500-7x)kg乙种原料;
(2)因为A一件可获利700元,生产一件B种产品获利1200元,
所以y=700x+1200(50-x)=60000-500x.
【点睛】考查了列一次函数,解题关键抓住题中的等量关系进行解题.
23.(1)上表反映了温度和距离地面高度之间的关系,距离地面高度是自变量,温度是因变量
(2)
(3)温度为时,距离地面的高度是千米
【分析】本题考查函数的定义,表格表示函数关系,求函数值;
(1)根据函数的定义即可求解;
(2)由表格可知当高度每上升时,温度下降,然后计算即可;
(3)将代入解析式,即可求解.
【详解】(1)解:上表反映了温度和距离地面高度之间的关系,距离地面高度是自变量,温度是因变量.
(2)根据表格数据知当高度每上升时,温度下降,
∴;
(3)将代入 ,
可得:,
解得 ,
答:温度为时,距离地面的高度是千米.
24.(1)N和t是变量,114是常量
(2)S和a是变量,2是常量
【分析】本题主要考查了常量与变量,熟练掌握常量与变量的定义是解题的关键.
(1)根据在这一变化过程中,是保持不变的量;和是可以取不同数值的量分析判断即可得解;
(2)根据在这一变化过程中,是保持不变的量;和是可以取不同数值的量分析判断即可得解.
【详解】(1)解:和是变量,是常量;
(2)解:和是变量,是常量.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
