山东省潍坊市2025年九年级下学期中考三模数学试卷(含答案)
文档属性
| 名称 | 山东省潍坊市2025年九年级下学期中考三模数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-18 20:11:24 | ||
图片预览




文档简介
参照秘密级管理★启用前 试卷类型:A
(
毕业学校
________________
姓名
____________________
考生号
_______________
座
号
____________
)2025年初中学业水平调研自测
数 学 试 题 2025.05
注意事项:
1.本试题满分150分,考试时间为120分钟;
2.答卷前,请将试卷和答题纸上的项目填涂清楚;
3.请在答题纸相应位置作答,不要超出答题区域,不要答错位置.
第I卷(选择题 共44分)
单项选择题:本题共6小题,每小题4分,每题只有一个选项符合题意,共计24分。
1.2025年世界运动会将于8月7日至8月17日在四川省成都市举行,是中国第二次举办世界运动会。下列各图都是成都世界运动会的预选图案,其中是轴对称图形的是( )
A. B. C. D.
2.紫砂壶,被誉为中国非物质文化遗产的瑰宝,以其独特的成型工艺和多样的造型式样著称,陶器所散发的古朴典雅之色更是引人入胜.如图所展示的是一把精湛工艺紫砂壶“景舟石瓢”,下面四幅图是此紫砂壶的俯视图的是( )
A. B. C. D.
3.如图,实数,,在数轴上的对应点分别是,,.若,互为相反数,则下列式子正确的是( )
A. B.
C. D.
4.若关于的一元二次方程没有实数根,则直线不经过的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在平面直角坐标系中,已知点,,如果将线段绕点逆时针旋转至,那么点的坐标是( )
A. B.
C. D.
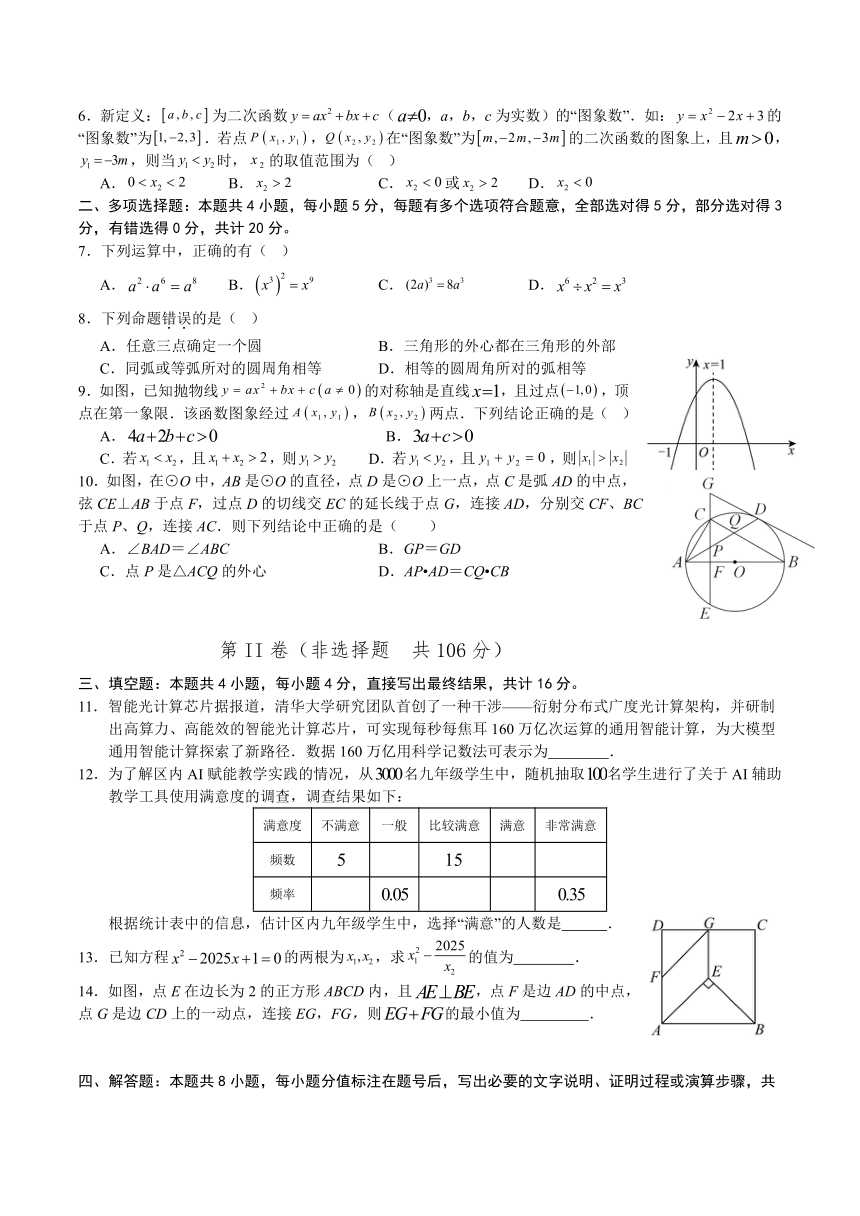
6.新定义:为二次函数(,a,b,c为实数)的“图象数”.如:的“图象数”为.若点,在“图象数”为的二次函数的图象上,且,,则当时,的取值范围为( )
A. B. C.或 D.
二、多项选择题:本题共4小题,每小题5分,每题有多个选项符合题意,全部选对得5分,部分选对得3
分,有错选得0分,共计20分。
7.下列运算中,正确的有( )
A. B. C. D.
8.下列命题错误的是( )
A.任意三点确定一个圆 B.三角形的外心都在三角形的外部
C.同弧或等弧所对的圆周角相等 D.相等的圆周角所对的弧相等
9.如图,已知抛物线的对称轴是直线,且过点,顶点在第一象限.该函数图象经过,两点.下列结论正确的是( )
A. B.
C.若,且,则 D.若,且,则
10.如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.则下列结论中正确的是( )
A.∠BAD=∠ABC B.GP=GD
C.点P是△ACQ的外心 D.AP AD=CQ CB
第II卷(非选择题 共106分)
三、填空题:本题共4小题,每小题4分,直接写出最终结果,共计16分。
11.智能光计算芯片据报道,清华大学研究团队首创了一种干涉——衍射分布式广度光计算架构,并研制出高算力、高能效的智能光计算芯片,可实现每秒每焦耳160万亿次运算的通用智能计算,为大模型通用智能计算探索了新路径.数据160万亿用科学记数法可表示为 .
12.为了解区内AI赋能教学实践的情况,从名九年级学生中,随机抽取名学生进行了关于AI辅助教学工具使用满意度的调查,调查结果如下:
满意度 不满意 一般 比较满意 满意 非常满意
频数
频率
根据统计表中的信息,估计区内九年级学生中,选择“满意”的人数是 .
13.已知方程的两根为,求的值为 .
14.如图,点E在边长为2的正方形ABCD内,且,点F是边AD的中点,点G是边CD上的一动点,连接EG,FG,则的最小值为 .
四、解答题:本题共8小题,每小题分值标注在题号后,写出必要的文字说明、证明过程或演算步骤,共
计90分。
15.(本题10分)
(1)解不等式组.
(2)先化简,再求值.,其中.
16.(本题9分)
如图,平行四边形中,对角线,于点E,于点F,
(1)求证:四边形是矩形.
(2)若,求的度数.
17.(本题9分)
潍坊市自2026年开始将施行新的中考政策,将历史、地理、生物三个科目列为考查科目,纳入等级考试评价,等级分为,,,,E五个等级.若规定:这两科考试成绩均达到等级及以上视作“地生会考成绩优秀”;两科考试成绩均达到等级及以上才可以报考普通高中.某校为了解本届八年级学生地理、生物的成绩情况,组织了这两科目的模拟考试,并从八年级学生中随机抽取了名学生的两科考试成绩制作了如下的统计图.根据这些信息,解答下列问题:
(1)被抽取的名学生中,某学生的生物模拟考试成绩为分,则该生的地理模拟考试成绩为________分;
(2)根据历届成绩分析,地理成绩达分及以上能评定为等级及以上,生物成绩达分及以上能评定为等级及以上.该校本届八年级共有学生人,请估计该校“地生会考成绩优秀”的学生人数;
(3)小沐同学在本次模拟考试中两科成绩均高于分,爸爸想奖励带她去看两场电影,但是目前只有四部电影上映(依次记为,,,),于是爸爸将四张完全相同的卡片分别写上,,,,背面朝上洗匀放好,要求小沐从中随机抽取两张卡片.请用列表或画树状图的方法,求小沐抽到的两张卡片恰好是和的概率.
18.(本题10分)
如图,一次函数的图象与反比例函数的图象在第一象限交于点,与x轴交于点.
(1)求k,m,n的值;
(2)点P在x轴上,,轴,交反比例函数的图象于点D,连接,求的面积.
19.(本题12分)
在有毒、缺氧或浓烟等危险环境开展侦查、搜救是消防救援的核心工作之一,救援人员常面临人身安全威胁,关键时刻需要可靠伙伴——消防机器狗,它能深入室内高危区,打通室内室外壁垒进行搜救,搭载的远距通讯模块,可实现远程操控与实时传图,为救援决策提供可视化信息.
图1是被困人员所处的楼梯横断面示意图.楼梯斜坡用表示,转角平台用表示,地面用表示.已知,垂足为米,米,米.
(1)求斜坡的坡比;
(2)如图2,当机器狗爬到斜坡上点处时,探测仪测得被困人员头顶的仰角为,继续前行到点处,恰好能搜集到被困人员全身的影像,此时探测仪在线段的延长线上,记作点.图2示意图中所有点均处于同一平面,,垂足分别为米,米,求的长.(参考数据:)
20.(本题13分)
如图,是的直径,C,G是上的点,过点的直线于点,交的延长线于点与交于点,且.
(1)求证:是的切线;
(2)若,求的度数;
(3)连接,在(2)的条件下,若,求的长.
21.(本题14分)
【发现问题】
星海湾大桥位于辽宁省大连市,是国内首座海上设重力式锚碇悬索桥,也是国内最长的海上双层桥梁.星海湾跨海大桥全长6千米,主桥为双塔三跨地锚式、双层通车悬索桥.主桥长820米,主桥主跨(两个主塔间的距离L)460米,边跨180米,跨径布置为180+460+180=820m.
如图是大桥的主跨,主跨悬索矢跨比(S:L)约为,悬索的最低处直接和桥梁相连,悬索和桥梁之间的吊杆间距10m,由于桥梁中间有车辆通过,灯光秀的光源放置在距桥梁上沿下方21米的桥梁中.
【提出问题】
星海大桥主跨上的吊杆的高度与它距最低点的水平距离有怎样的数量关系
【分析问题】
小明了解到,大桥主跨上连接两座主塔之间的悬索可以看成是抛物线的一部分,结合二次函数相关内容和查阅到的相关数据,建立适当的坐标系,就可以求出这条抛物线表示的二次函数,便可解决问题.
【解决问题】
小明利用查阅到的相关数据,为解题方便,小明以抛物线的顶点(大桥主跨上悬索的最低点)为原点,以主跨的中轴为y轴,建立平面直角坐标系(如图3).
(1)请直接写出以下问题的答案:
①右侧悬索最高点B的坐标;
②y与x的函数解析式;
③最长的吊杆的长度;
(2)某游客在远处海滩正对大桥主跨的位置,看到一个由多辆彩车组成的150米的车队,车队以50米/分的速度通过大桥主跨,彩车高于桥梁部分均为6.9米.在彩车通过大桥主跨过程中,该游客在悬索上方能看到彩车的时间是否超过6分钟;
(3)如图3,灯光秀中一个射灯光源C(,),位于悬索最低点左下方,即距悬索最低点的水平距离为70米的地方,它所发出的射线状光线,刚好经过右侧悬索的最高点B,现在想在这个光源的水平右侧再放置一个同样的平行光源,应该在什么范围内放置,才能保证该光源所射出的光线照到右侧悬索上
22.(本题13分)
【问题提出】
用n个圆最多能把平面分成几个区域?
【问题探究】
为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:如图1,一个圆能把平面分成2个区域.
探究二:用2个圆最多能把平面分成几个区域?
如图2,在探究一的基础上,为了使分成的区域最多,应使新增加的圆与前1个圆有2个交点,将新增加的圆分成2部分,从而增加2个区域,所以,用2个圆最多能把平面分成4个区域.
探究三:用3个圆最多能把平面分成几个区域?
如图3,在探究二的基础上,为了使分成的区域最多,应使新增加的圆与前2个圆分别有2个交点,将新增加的圆分成部分,从而增加4个区域,所以,用3个圆最多能把平面分成8个区域.
(1)用4个圆最多能把平面分成几个区域?仿照前面的探究方法,写出解答过程,不需画图.
【一般结论】用n个圆最多能把平面分成几个区域?
(2)为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成______________部分,从而增加___________________个区域,所以,用n个圆最多能把平面分______________个区域.(将结果进行化简)
【结论应用】
(3)①用10个圆最多能把平面分成_________个区域;
②用___________个圆最多能把平面分成422个区域.
2025年初中学业水平调研自测
数学试题参考答案与评分标准
2025.06
单项选择题,每小题4分,共24分。选对得4分,错选得0分。
题号 1 2 3 4 5 6
答案 A D B C B C
多项选择题,每小题5分,共20分。全部选对得5分,部分选对得3分,有错选的得0分。
题号 7 8 9 10
答案 AC ABD AC BCD
题块一、填空题,每小题4分,共16分。书写正确得4分,除特殊标注外答案唯一。
12.1200(人)(不写单位不扣分) 13. 14.##(两种写法均可)
题块二、解答题15题
解:(1),
解不等式①得:,..............................(1分)
解不等式②得:,..............................(2分)
∴不等式组的解集为,..............................(4分)
(2)解:
..............................(5分)
..............................(6分)
..............................(7分)
∵
∴..............................(8分)
∴原式..............................(10分)
题块三、解答题16题
(1)证明:,,
,
在和中,
,
,..............................(3分)
,
∵四边形是平行四边形,
,
,
∴四边形是矩形;..............................(5分)
(2)解:由(1)得:四边形是矩形,
,,
,
在直角三角形中,,
...............................(9分)
题块四、解答题17题
(1)解:;..............................(2分,只写出最后答案即可)
(2)从八年级学生中随机抽取的名学生的两科考试成绩中,地理成绩达分及以上同时生物成绩达分及以上有人,
∴(人),
答:该校地生会考成绩优秀的学生人数约为人;..............................(5分)
(3)列表如下:
第二张第一张
一共有种等可能的结果,其中抽到两张卡片恰好是和的可能有种,
∴(两张卡片恰好是和).
答:小沐抽到的两张卡片恰好是和的概率为...............................(9分)
题块五、解答题18题
(1)解:根据题意得,将代入得,
解得..............................(1分)
∴一次函数
将代入得,;
∴..............................(3分)
∴将代入得,
∴;..............................(4分)
(2)解:如图所示,过作轴于点,
∵
∴
∵,
∴
将代入
∴
∴..............................(8分)
...............................(10分)
题块六、解答题19题
(1)解:过点作,交于点,如图:
,
∴,
∴四边形是矩形,)
,
,,
,
在中,,..............................(3分)
∴斜坡的坡比为;..............................(5分)
(2)解:过点作交于点,作交延长线于点,如图:
根据题意可知:
,
在中,,
米,..............................(7分)
米,..............................(8分)
由,
,
,
在中,米,
米,
∴的长米...............................(12分)
题块七、解答题20题
(1)证明:如图所示,连接,
∵,
∴,
∵
∴,
∴,
∵,
∴,
∵是的半径,
∴是的切线;..............................(4分)
(2)解:∵,
∴,..............................(5分)
∴,
∴,
∴,..............................(6分)
∵,
∴,
∴,
∵,
∴,..............................(7分)
∴;..............................(8分)
(3)解:如图2,过A作于H,
∵,
∴,
∴,..............................(9分)
∵,
∴,
∴,,..............................(10分)
∵,
∴,
∴,
∴,,..............................(11分)
∴,..............................(12分)
在中,由勾股定理得...............................(13分)
题块八、解答题21题
(1)①如图,作轴于D点,
由题意得,
,
,
,
,
∴点B的坐标为;..............................(1分,只写出最后答案即可)
②设,
把代入得,
解得,
∴y与x的函数解析式为:;..............................(3分,只写出最后答案即可)
③如图,设最长的吊杆为EF,
∵吊杆间距10m,
∴,
,
由得,时,,
,
∴最长的吊杆的长度约为63m...............................(5分,只写出最后答案即可)
(2)如图,作轴,交抛物线于M、N两点,
由题意知,代入抛物线解析式得,..............................(6分)
解得,,
,,..............................(7分)
,
∴游客在悬索上方能看到彩车的时间为:,
∴游客在悬索上方能看到彩车的时间不超过6分钟. ..............................(8分)
(3)
设光源放在G点时,光线与悬索只有一个交点,
设直线的表达式为,则
,
解得,
∴直线的表达式为:...............................(9分)
,
∴直线与直线的k相同,
设直线的表达式为,
联立,
得,
整理得,..............................(10分)
∵直线与抛物线只有一个交点,
,
解得,..............................(11分)
∴直线的表达式为...............................(12分)
当时,,
解得,
∴,..............................(13分)
∴光源应放在和之间,才能保证该光源所射出的光线照到右侧悬索上...............................(14分)
题块九、解答题22题
解:(1)在探究三的基础上,为了使分成的区域最多,应使新增加的圆与前3个圆分别有2个交点,将新增的圆分成部分,从而增加6个区域,所以,用4个圆最多能把平面分成2+2×1+2×2+2×3=14个区域;
..............................(3分,不写过程直接写结论得1分)
(2)为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成(2n-2)部分,从而增加(2n-2)个区域,所以,用n个圆最多能把平面分成区域数为
2+2×1+2×2+2×3+2×4+…+2(n-1),
=2+2(1+2+3+…+n-1),
=2+2,
,
=;
故答案为:(2n-2);(2n-2);;..............................(9分,写对1空给2分,只写出最后答案即可)
(3)①用10个圆,即n=10,;..............................(11分,只写出最后答案即可)
②设n个圆最多能把平面分成422个区域,
可得方程,
整理得,
因式分解得,
解得或(舍去),
∴用21个圆最多能把平面分成422个区域.
故答案为:21...............................(13分,只写出最后答案即可)
(
毕业学校
________________
姓名
____________________
考生号
_______________
座
号
____________
)2025年初中学业水平调研自测
数 学 试 题 2025.05
注意事项:
1.本试题满分150分,考试时间为120分钟;
2.答卷前,请将试卷和答题纸上的项目填涂清楚;
3.请在答题纸相应位置作答,不要超出答题区域,不要答错位置.
第I卷(选择题 共44分)
单项选择题:本题共6小题,每小题4分,每题只有一个选项符合题意,共计24分。
1.2025年世界运动会将于8月7日至8月17日在四川省成都市举行,是中国第二次举办世界运动会。下列各图都是成都世界运动会的预选图案,其中是轴对称图形的是( )
A. B. C. D.
2.紫砂壶,被誉为中国非物质文化遗产的瑰宝,以其独特的成型工艺和多样的造型式样著称,陶器所散发的古朴典雅之色更是引人入胜.如图所展示的是一把精湛工艺紫砂壶“景舟石瓢”,下面四幅图是此紫砂壶的俯视图的是( )
A. B. C. D.
3.如图,实数,,在数轴上的对应点分别是,,.若,互为相反数,则下列式子正确的是( )
A. B.
C. D.
4.若关于的一元二次方程没有实数根,则直线不经过的象限为( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
5.如图,在平面直角坐标系中,已知点,,如果将线段绕点逆时针旋转至,那么点的坐标是( )
A. B.
C. D.
6.新定义:为二次函数(,a,b,c为实数)的“图象数”.如:的“图象数”为.若点,在“图象数”为的二次函数的图象上,且,,则当时,的取值范围为( )
A. B. C.或 D.
二、多项选择题:本题共4小题,每小题5分,每题有多个选项符合题意,全部选对得5分,部分选对得3
分,有错选得0分,共计20分。
7.下列运算中,正确的有( )
A. B. C. D.
8.下列命题错误的是( )
A.任意三点确定一个圆 B.三角形的外心都在三角形的外部
C.同弧或等弧所对的圆周角相等 D.相等的圆周角所对的弧相等
9.如图,已知抛物线的对称轴是直线,且过点,顶点在第一象限.该函数图象经过,两点.下列结论正确的是( )
A. B.
C.若,且,则 D.若,且,则
10.如图,在⊙O中,AB是⊙O的直径,点D是⊙O上一点,点C是弧AD的中点,弦CE⊥AB于点F,过点D的切线交EC的延长线于点G,连接AD,分别交CF、BC于点P、Q,连接AC.则下列结论中正确的是( )
A.∠BAD=∠ABC B.GP=GD
C.点P是△ACQ的外心 D.AP AD=CQ CB
第II卷(非选择题 共106分)
三、填空题:本题共4小题,每小题4分,直接写出最终结果,共计16分。
11.智能光计算芯片据报道,清华大学研究团队首创了一种干涉——衍射分布式广度光计算架构,并研制出高算力、高能效的智能光计算芯片,可实现每秒每焦耳160万亿次运算的通用智能计算,为大模型通用智能计算探索了新路径.数据160万亿用科学记数法可表示为 .
12.为了解区内AI赋能教学实践的情况,从名九年级学生中,随机抽取名学生进行了关于AI辅助教学工具使用满意度的调查,调查结果如下:
满意度 不满意 一般 比较满意 满意 非常满意
频数
频率
根据统计表中的信息,估计区内九年级学生中,选择“满意”的人数是 .
13.已知方程的两根为,求的值为 .
14.如图,点E在边长为2的正方形ABCD内,且,点F是边AD的中点,点G是边CD上的一动点,连接EG,FG,则的最小值为 .
四、解答题:本题共8小题,每小题分值标注在题号后,写出必要的文字说明、证明过程或演算步骤,共
计90分。
15.(本题10分)
(1)解不等式组.
(2)先化简,再求值.,其中.
16.(本题9分)
如图,平行四边形中,对角线,于点E,于点F,
(1)求证:四边形是矩形.
(2)若,求的度数.
17.(本题9分)
潍坊市自2026年开始将施行新的中考政策,将历史、地理、生物三个科目列为考查科目,纳入等级考试评价,等级分为,,,,E五个等级.若规定:这两科考试成绩均达到等级及以上视作“地生会考成绩优秀”;两科考试成绩均达到等级及以上才可以报考普通高中.某校为了解本届八年级学生地理、生物的成绩情况,组织了这两科目的模拟考试,并从八年级学生中随机抽取了名学生的两科考试成绩制作了如下的统计图.根据这些信息,解答下列问题:
(1)被抽取的名学生中,某学生的生物模拟考试成绩为分,则该生的地理模拟考试成绩为________分;
(2)根据历届成绩分析,地理成绩达分及以上能评定为等级及以上,生物成绩达分及以上能评定为等级及以上.该校本届八年级共有学生人,请估计该校“地生会考成绩优秀”的学生人数;
(3)小沐同学在本次模拟考试中两科成绩均高于分,爸爸想奖励带她去看两场电影,但是目前只有四部电影上映(依次记为,,,),于是爸爸将四张完全相同的卡片分别写上,,,,背面朝上洗匀放好,要求小沐从中随机抽取两张卡片.请用列表或画树状图的方法,求小沐抽到的两张卡片恰好是和的概率.
18.(本题10分)
如图,一次函数的图象与反比例函数的图象在第一象限交于点,与x轴交于点.
(1)求k,m,n的值;
(2)点P在x轴上,,轴,交反比例函数的图象于点D,连接,求的面积.
19.(本题12分)
在有毒、缺氧或浓烟等危险环境开展侦查、搜救是消防救援的核心工作之一,救援人员常面临人身安全威胁,关键时刻需要可靠伙伴——消防机器狗,它能深入室内高危区,打通室内室外壁垒进行搜救,搭载的远距通讯模块,可实现远程操控与实时传图,为救援决策提供可视化信息.
图1是被困人员所处的楼梯横断面示意图.楼梯斜坡用表示,转角平台用表示,地面用表示.已知,垂足为米,米,米.
(1)求斜坡的坡比;
(2)如图2,当机器狗爬到斜坡上点处时,探测仪测得被困人员头顶的仰角为,继续前行到点处,恰好能搜集到被困人员全身的影像,此时探测仪在线段的延长线上,记作点.图2示意图中所有点均处于同一平面,,垂足分别为米,米,求的长.(参考数据:)
20.(本题13分)
如图,是的直径,C,G是上的点,过点的直线于点,交的延长线于点与交于点,且.
(1)求证:是的切线;
(2)若,求的度数;
(3)连接,在(2)的条件下,若,求的长.
21.(本题14分)
【发现问题】
星海湾大桥位于辽宁省大连市,是国内首座海上设重力式锚碇悬索桥,也是国内最长的海上双层桥梁.星海湾跨海大桥全长6千米,主桥为双塔三跨地锚式、双层通车悬索桥.主桥长820米,主桥主跨(两个主塔间的距离L)460米,边跨180米,跨径布置为180+460+180=820m.
如图是大桥的主跨,主跨悬索矢跨比(S:L)约为,悬索的最低处直接和桥梁相连,悬索和桥梁之间的吊杆间距10m,由于桥梁中间有车辆通过,灯光秀的光源放置在距桥梁上沿下方21米的桥梁中.
【提出问题】
星海大桥主跨上的吊杆的高度与它距最低点的水平距离有怎样的数量关系
【分析问题】
小明了解到,大桥主跨上连接两座主塔之间的悬索可以看成是抛物线的一部分,结合二次函数相关内容和查阅到的相关数据,建立适当的坐标系,就可以求出这条抛物线表示的二次函数,便可解决问题.
【解决问题】
小明利用查阅到的相关数据,为解题方便,小明以抛物线的顶点(大桥主跨上悬索的最低点)为原点,以主跨的中轴为y轴,建立平面直角坐标系(如图3).
(1)请直接写出以下问题的答案:
①右侧悬索最高点B的坐标;
②y与x的函数解析式;
③最长的吊杆的长度;
(2)某游客在远处海滩正对大桥主跨的位置,看到一个由多辆彩车组成的150米的车队,车队以50米/分的速度通过大桥主跨,彩车高于桥梁部分均为6.9米.在彩车通过大桥主跨过程中,该游客在悬索上方能看到彩车的时间是否超过6分钟;
(3)如图3,灯光秀中一个射灯光源C(,),位于悬索最低点左下方,即距悬索最低点的水平距离为70米的地方,它所发出的射线状光线,刚好经过右侧悬索的最高点B,现在想在这个光源的水平右侧再放置一个同样的平行光源,应该在什么范围内放置,才能保证该光源所射出的光线照到右侧悬索上
22.(本题13分)
【问题提出】
用n个圆最多能把平面分成几个区域?
【问题探究】
为了解决上面的数学问题,我们采取一般问题特殊化的策略,先从最简单情形入手,再逐次递进,最后猜想得出结论.
探究一:如图1,一个圆能把平面分成2个区域.
探究二:用2个圆最多能把平面分成几个区域?
如图2,在探究一的基础上,为了使分成的区域最多,应使新增加的圆与前1个圆有2个交点,将新增加的圆分成2部分,从而增加2个区域,所以,用2个圆最多能把平面分成4个区域.
探究三:用3个圆最多能把平面分成几个区域?
如图3,在探究二的基础上,为了使分成的区域最多,应使新增加的圆与前2个圆分别有2个交点,将新增加的圆分成部分,从而增加4个区域,所以,用3个圆最多能把平面分成8个区域.
(1)用4个圆最多能把平面分成几个区域?仿照前面的探究方法,写出解答过程,不需画图.
【一般结论】用n个圆最多能把平面分成几个区域?
(2)为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成______________部分,从而增加___________________个区域,所以,用n个圆最多能把平面分______________个区域.(将结果进行化简)
【结论应用】
(3)①用10个圆最多能把平面分成_________个区域;
②用___________个圆最多能把平面分成422个区域.
2025年初中学业水平调研自测
数学试题参考答案与评分标准
2025.06
单项选择题,每小题4分,共24分。选对得4分,错选得0分。
题号 1 2 3 4 5 6
答案 A D B C B C
多项选择题,每小题5分,共20分。全部选对得5分,部分选对得3分,有错选的得0分。
题号 7 8 9 10
答案 AC ABD AC BCD
题块一、填空题,每小题4分,共16分。书写正确得4分,除特殊标注外答案唯一。
12.1200(人)(不写单位不扣分) 13. 14.##(两种写法均可)
题块二、解答题15题
解:(1),
解不等式①得:,..............................(1分)
解不等式②得:,..............................(2分)
∴不等式组的解集为,..............................(4分)
(2)解:
..............................(5分)
..............................(6分)
..............................(7分)
∵
∴..............................(8分)
∴原式..............................(10分)
题块三、解答题16题
(1)证明:,,
,
在和中,
,
,..............................(3分)
,
∵四边形是平行四边形,
,
,
∴四边形是矩形;..............................(5分)
(2)解:由(1)得:四边形是矩形,
,,
,
在直角三角形中,,
...............................(9分)
题块四、解答题17题
(1)解:;..............................(2分,只写出最后答案即可)
(2)从八年级学生中随机抽取的名学生的两科考试成绩中,地理成绩达分及以上同时生物成绩达分及以上有人,
∴(人),
答:该校地生会考成绩优秀的学生人数约为人;..............................(5分)
(3)列表如下:
第二张第一张
一共有种等可能的结果,其中抽到两张卡片恰好是和的可能有种,
∴(两张卡片恰好是和).
答:小沐抽到的两张卡片恰好是和的概率为...............................(9分)
题块五、解答题18题
(1)解:根据题意得,将代入得,
解得..............................(1分)
∴一次函数
将代入得,;
∴..............................(3分)
∴将代入得,
∴;..............................(4分)
(2)解:如图所示,过作轴于点,
∵
∴
∵,
∴
将代入
∴
∴..............................(8分)
...............................(10分)
题块六、解答题19题
(1)解:过点作,交于点,如图:
,
∴,
∴四边形是矩形,)
,
,,
,
在中,,..............................(3分)
∴斜坡的坡比为;..............................(5分)
(2)解:过点作交于点,作交延长线于点,如图:
根据题意可知:
,
在中,,
米,..............................(7分)
米,..............................(8分)
由,
,
,
在中,米,
米,
∴的长米...............................(12分)
题块七、解答题20题
(1)证明:如图所示,连接,
∵,
∴,
∵
∴,
∴,
∵,
∴,
∵是的半径,
∴是的切线;..............................(4分)
(2)解:∵,
∴,..............................(5分)
∴,
∴,
∴,..............................(6分)
∵,
∴,
∴,
∵,
∴,..............................(7分)
∴;..............................(8分)
(3)解:如图2,过A作于H,
∵,
∴,
∴,..............................(9分)
∵,
∴,
∴,,..............................(10分)
∵,
∴,
∴,
∴,,..............................(11分)
∴,..............................(12分)
在中,由勾股定理得...............................(13分)
题块八、解答题21题
(1)①如图,作轴于D点,
由题意得,
,
,
,
,
∴点B的坐标为;..............................(1分,只写出最后答案即可)
②设,
把代入得,
解得,
∴y与x的函数解析式为:;..............................(3分,只写出最后答案即可)
③如图,设最长的吊杆为EF,
∵吊杆间距10m,
∴,
,
由得,时,,
,
∴最长的吊杆的长度约为63m...............................(5分,只写出最后答案即可)
(2)如图,作轴,交抛物线于M、N两点,
由题意知,代入抛物线解析式得,..............................(6分)
解得,,
,,..............................(7分)
,
∴游客在悬索上方能看到彩车的时间为:,
∴游客在悬索上方能看到彩车的时间不超过6分钟. ..............................(8分)
(3)
设光源放在G点时,光线与悬索只有一个交点,
设直线的表达式为,则
,
解得,
∴直线的表达式为:...............................(9分)
,
∴直线与直线的k相同,
设直线的表达式为,
联立,
得,
整理得,..............................(10分)
∵直线与抛物线只有一个交点,
,
解得,..............................(11分)
∴直线的表达式为...............................(12分)
当时,,
解得,
∴,..............................(13分)
∴光源应放在和之间,才能保证该光源所射出的光线照到右侧悬索上...............................(14分)
题块九、解答题22题
解:(1)在探究三的基础上,为了使分成的区域最多,应使新增加的圆与前3个圆分别有2个交点,将新增的圆分成部分,从而增加6个区域,所以,用4个圆最多能把平面分成2+2×1+2×2+2×3=14个区域;
..............................(3分,不写过程直接写结论得1分)
(2)为了使分成的区域最多,应使新增加的圆与前个圆分别有2个交点,将新增加的圆分成(2n-2)部分,从而增加(2n-2)个区域,所以,用n个圆最多能把平面分成区域数为
2+2×1+2×2+2×3+2×4+…+2(n-1),
=2+2(1+2+3+…+n-1),
=2+2,
,
=;
故答案为:(2n-2);(2n-2);;..............................(9分,写对1空给2分,只写出最后答案即可)
(3)①用10个圆,即n=10,;..............................(11分,只写出最后答案即可)
②设n个圆最多能把平面分成422个区域,
可得方程,
整理得,
因式分解得,
解得或(舍去),
∴用21个圆最多能把平面分成422个区域.
故答案为:21...............................(13分,只写出最后答案即可)
同课章节目录
