第十八章《平行四边形》阶段测试卷(一) (含答案)2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十八章《平行四边形》阶段测试卷(一) (含答案)2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 125.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 00:00:00 | ||
图片预览




文档简介
第十八章《平行四边形》阶段测试卷(一)
(考试范围:18.1 解答参考时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
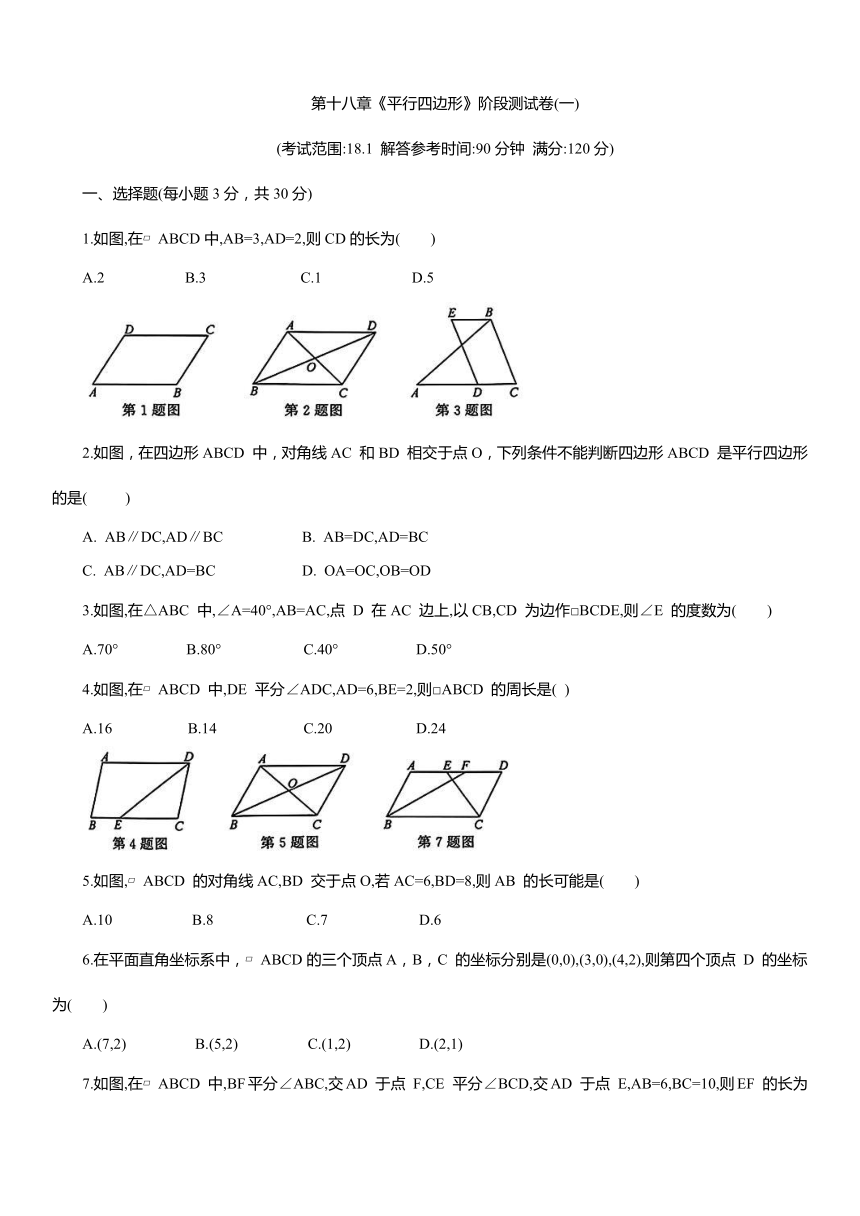
1.如图,在 ABCD中,AB=3,AD=2,则CD的长为( )
A.2 B.3 C.1 D.5
2.如图,在四边形ABCD 中,对角线AC 和BD 相交于点O,下列条件不能判断四边形ABCD 是平行四边形的是( )
A. AB∥DC,AD∥BC B. AB=DC,AD=BC
C. AB∥DC,AD=BC D. OA=OC,OB=OD
3.如图,在△ABC 中,∠A=40°,AB=AC,点 D 在AC 边上,以CB,CD 为边作□BCDE,则∠E 的度数为( )
A.70° B.80° C.40° D.50°
4.如图,在 ABCD 中,DE 平分∠ADC,AD=6,BE=2,则□ABCD 的周长是( )
A.16 B.14 C.20 D.24
5.如图, ABCD 的对角线AC,BD 交于点O,若AC=6,BD=8,则AB 的长可能是( )
A.10 B.8 C.7 D.6
6.在平面直角坐标系中, ABCD的三个顶点A,B,C 的坐标分别是(0,0),(3,0),(4,2),则第四个顶点 D 的坐标为( )
A.(7,2) B.(5,2) C.(1,2) D.(2,1)
7.如图,在 ABCD 中,BF平分∠ABC,交AD 于点 F,CE 平分∠BCD,交AD 于点 E,AB=6,BC=10,则EF 的长为( )
A.1 B.2 C.3 D.4
8.如图,在四边形ABCD 中,M 是对角线BD 的中点,E,F 分别是边AB,CD 的中点.若AD=BC,∠EMF=132°,则∠MFE的度数为( )
A.66° B.48° C.38° D.24°
9.如图,在 中,CE 平分 ,交 AB 于点E, EB=5,ED=4.则CE 的长是( )
10.如图,在 ABCD 中,∠ABC=45°,BC=4,F 是CD 上的一个动点,以FA,FB 为邻边作另一个□AEBF,连接EF,则线段 EF 的最小值为( )
A.5 C.6
二、填空题(每小题3分,共15分)
11.如图, ABCD中,CE⊥AB 于点 E,若∠A=115°,则∠BCE= 度.
12.如图,点E,F 分别在 ABCD 的边BC,AD 上,请你添加一个条件(只添一个即可),使四边形AECF 是平行四边形,你所添加的条件是 .
13.在 ABCD中,对角线AC,BD相交于点O,AB=3,BC=5,则OA 的取值范围为 .
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC 是 ABCD 的对角线,点 E 在AC 上,AD=AE=BE,∠D=102°,则∠BAC 的度数是 .
15.如图,在等边△ABC 中,BC=8cm,射线AG∥BC,点E 从点A 出发沿射线AG 以1 cm/s的速度运动,点 F 从点 B 出发沿射线BC 以3cm/s的速度运动.设运动时间为t(s),若以A,C,E,F为顶点的四边形是平行四边形,则t 的值为
三、解答题(共9小题,共75分)
16.(本题6分)如图,在 中,延长AB 至点E,延长CD至点F,使得 连接EF,与对角线 AC交于点O.求证:
17.(本题6分)如图,四边形 ABCD 是平行四边形,BE 平分 DF 平分 求证:四边形 DEBF 是平行四边形.
18.(本题6分)如图,点B,E,C,F在一条直线上, DF,BE=CF.
(1)求证:
(2)连接AD,求证:四边形ABED 是平行四边形.
19.(本题8分)如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.
(1)求证:AE⊥BF;
(2)若∠BCD=80°,求∠AEC 的度数.
20.(本题8分)如图,在 ABCD中,AB=AE.若AE平分∠DAB.
(1)求证:△ABC≌△EAD;
(2)若∠EAC=25°,求∠AED 的度数.
21.(本题8分)(1)如图1,在△ABC 中,D,E 分别是边AB,AC的中点.若BC=6,直接写出 DE 的长;
(2)如图2,在四边形ABCD中,E,F 分别是AB,AD 的中点.若BC=5,CD=4,EF=1.5,∠AFE=45°,求∠ADC 的度数.
22.(本题10分)如图1,在 中,O为对角线AC 的中点,过点O 的直线EF 分别交AB,CD 于点E,F.
(1)求证:
(2)如图2,若 求AE 的长.
23.(本题11分)(1)问题背景:如图1,AE平分. 于点E,交AB 于点D,F为BC的中点,连接EF.求证:.
(2)尝试应用:如图2,BE平分 于点E,F 为AC的中点,连接EF.. 求EF 的长.
24.(本题12分)如图1,在平面直角坐标系中,四边形 ABCD的顶点坐标分别为A(0,a),B(b,0),C(c,0),D(d,a),且OD平分 a,b,c 满足关系式
(1)判断四边形 ABCD 的形状并证明你的结论;
(2)如图 2,M 为CD 中点,将 沿 BM 折叠得到 延长BN交AD 于点F.求证:
(3)如图3,过点 C作 于点E,连接BE,求 的值.
1. B 2. C 3. A 4. C 5. D 6. C 7. B 8. D 9. C
10. D 解:设EF 交AB 于点 H,当 FH⊥AB 时,FH 的值最小,EF=2FH 的值也最小.过点C作CG⊥AB 于点G.
∴CG=2 ,∴FH=2
∴线段EF 的最小值为.
11.25 12. AF=CE13.115.2或4 解:当点 F 在点 C 的左侧时,AE=t cm,BF=3t cm,则CF=(8-3t) cm,∵AG∥BC,∴当AE=CF时,得□AECF,即t=8-3t,解得t=2;当点 F 在点C 的右侧时,t=3t-8,解得t=4.综上所述,当t=2或4.
16.证明:∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD.∵BE=DF,
∴AB+BE=CD+DF,即AE=CF,
∵AB∥CD,∴∠E=∠F,∠OAE=∠OCF,
∴△AOE≌△COF(ASA),∴OE=OF.
17.证明:易证∠EBC=∠EDF=∠DFC,得BE∥DF,又ED∥BF,四边形 DEBF 是平行四边形.
18.证明:(1)∵BE=CF,∴BE+EC=CF+EC,∴BC=EF.又∵AB=DE,AC=DF,∴△ABC≌△DEF(SSS);
(2)∵△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.
又∵AB=DE,∴四边形ABED 是平行四边形.
19.解:(1)∵AB=AF,∠BAE=∠FAE,∴AE⊥BF;
(2)易证∠ABC=100°,AB=BE,
∴∠BEA=40°,∠AEC=140°.
20.解:(1)∵四边形ABCD 为平行四边形,
∴AD∥BC,AD=BC.∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE,∴△ABC≌△EAD(SAS);
(2)∵△ABC≌△EAD,∴∠AED=∠BAC.
∵AE平分∠DAB,∴∠DAE=∠BAE.
又∵∠DAE=∠AEB,∴∠BAE=∠AEB=∠B,
∴△ABE 为等边三角形,∴∠BAE=60°.
∵∠EAC=25°,∴∠BAC=85°,∴∠AED=85°.
21.解:(1)∵D,E 分别是边AB,AC的中点,
∴DE 是△ABC 的中位线,
(2)连接BD.∵E,F分别是边AB,AD的中点,
∴BD=2EF=3,EF∥BD,∴∠ADB=∠AFE=45°.
∵BC=5,CD=4,∴BC =25,BD +CD =25,
∴∠ADC=∠ADB+∠BDC=135°.
22.解:(1)易得△AOE≌△COF,∴AE=CF.
∵AB=CD,∴BE=DF;
(2)连接CE,过点C作CH⊥AB,交AB 的延长线于点 H.
∵□ABCD,∠ABC=135°,AD=4
∴∠CBH=45°,BC=4
又∵∠H=90°,∴∠BCH=45°,∴CH=BH=4.
设AE=x,则BE=8-x,
∵EF 垂直平分AC,∴CE=AE=x.
∵在Rt△CEH 中,
解得 ∴AE的长为
23.解:(1)∵AE平分∠CAB,CD⊥AE,
∴AC=AD,E 为CD 中点.∵F为BC 的中点,
∴EF 为△BCD 的中位线,.
又∵BD=AB-AD=AB-AC,∴EF= (AB-AC);
(2)延长AE,BC 交于点D,则AB=BD,E 为AD 中点.同
(1)可得
24.解:(1)四边形ABCD 为平行四边形.
∴2a-6=0且a+b-c=0,∴c-b=a=3,
∴BC=c-b=a=3,∴A(0,3),D(d,3),∴AD∥BC.
∵OD 平分∠AOC,∴∠AOD=∠DOC=∠ADO=45°,
∴AD=OA=3,∴AD=BC,∴四边形ABCD为平行四边形;
(2)延长BM,FD 交于点G.可得△BCM≌△GDM,
∴DG=BC=BN,∠G=∠MBC=∠FBM,
∴BF=GF,∴FD=FN;
(3)连接AE,延长CE 交 y轴于点 Q,易得△BOE≌△AQE,得等腰直角
(考试范围:18.1 解答参考时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,在 ABCD中,AB=3,AD=2,则CD的长为( )
A.2 B.3 C.1 D.5
2.如图,在四边形ABCD 中,对角线AC 和BD 相交于点O,下列条件不能判断四边形ABCD 是平行四边形的是( )
A. AB∥DC,AD∥BC B. AB=DC,AD=BC
C. AB∥DC,AD=BC D. OA=OC,OB=OD
3.如图,在△ABC 中,∠A=40°,AB=AC,点 D 在AC 边上,以CB,CD 为边作□BCDE,则∠E 的度数为( )
A.70° B.80° C.40° D.50°
4.如图,在 ABCD 中,DE 平分∠ADC,AD=6,BE=2,则□ABCD 的周长是( )
A.16 B.14 C.20 D.24
5.如图, ABCD 的对角线AC,BD 交于点O,若AC=6,BD=8,则AB 的长可能是( )
A.10 B.8 C.7 D.6
6.在平面直角坐标系中, ABCD的三个顶点A,B,C 的坐标分别是(0,0),(3,0),(4,2),则第四个顶点 D 的坐标为( )
A.(7,2) B.(5,2) C.(1,2) D.(2,1)
7.如图,在 ABCD 中,BF平分∠ABC,交AD 于点 F,CE 平分∠BCD,交AD 于点 E,AB=6,BC=10,则EF 的长为( )
A.1 B.2 C.3 D.4
8.如图,在四边形ABCD 中,M 是对角线BD 的中点,E,F 分别是边AB,CD 的中点.若AD=BC,∠EMF=132°,则∠MFE的度数为( )
A.66° B.48° C.38° D.24°
9.如图,在 中,CE 平分 ,交 AB 于点E, EB=5,ED=4.则CE 的长是( )
10.如图,在 ABCD 中,∠ABC=45°,BC=4,F 是CD 上的一个动点,以FA,FB 为邻边作另一个□AEBF,连接EF,则线段 EF 的最小值为( )
A.5 C.6
二、填空题(每小题3分,共15分)
11.如图, ABCD中,CE⊥AB 于点 E,若∠A=115°,则∠BCE= 度.
12.如图,点E,F 分别在 ABCD 的边BC,AD 上,请你添加一个条件(只添一个即可),使四边形AECF 是平行四边形,你所添加的条件是 .
13.在 ABCD中,对角线AC,BD相交于点O,AB=3,BC=5,则OA 的取值范围为 .
14.在探索数学名题“尺规三等分角”的过程中,有下面的问题:如图,AC 是 ABCD 的对角线,点 E 在AC 上,AD=AE=BE,∠D=102°,则∠BAC 的度数是 .
15.如图,在等边△ABC 中,BC=8cm,射线AG∥BC,点E 从点A 出发沿射线AG 以1 cm/s的速度运动,点 F 从点 B 出发沿射线BC 以3cm/s的速度运动.设运动时间为t(s),若以A,C,E,F为顶点的四边形是平行四边形,则t 的值为
三、解答题(共9小题,共75分)
16.(本题6分)如图,在 中,延长AB 至点E,延长CD至点F,使得 连接EF,与对角线 AC交于点O.求证:
17.(本题6分)如图,四边形 ABCD 是平行四边形,BE 平分 DF 平分 求证:四边形 DEBF 是平行四边形.
18.(本题6分)如图,点B,E,C,F在一条直线上, DF,BE=CF.
(1)求证:
(2)连接AD,求证:四边形ABED 是平行四边形.
19.(本题8分)如图,在 ABCD中,用直尺和圆规作∠BAD的平分线AG交BC 于点E.
(1)求证:AE⊥BF;
(2)若∠BCD=80°,求∠AEC 的度数.
20.(本题8分)如图,在 ABCD中,AB=AE.若AE平分∠DAB.
(1)求证:△ABC≌△EAD;
(2)若∠EAC=25°,求∠AED 的度数.
21.(本题8分)(1)如图1,在△ABC 中,D,E 分别是边AB,AC的中点.若BC=6,直接写出 DE 的长;
(2)如图2,在四边形ABCD中,E,F 分别是AB,AD 的中点.若BC=5,CD=4,EF=1.5,∠AFE=45°,求∠ADC 的度数.
22.(本题10分)如图1,在 中,O为对角线AC 的中点,过点O 的直线EF 分别交AB,CD 于点E,F.
(1)求证:
(2)如图2,若 求AE 的长.
23.(本题11分)(1)问题背景:如图1,AE平分. 于点E,交AB 于点D,F为BC的中点,连接EF.求证:.
(2)尝试应用:如图2,BE平分 于点E,F 为AC的中点,连接EF.. 求EF 的长.
24.(本题12分)如图1,在平面直角坐标系中,四边形 ABCD的顶点坐标分别为A(0,a),B(b,0),C(c,0),D(d,a),且OD平分 a,b,c 满足关系式
(1)判断四边形 ABCD 的形状并证明你的结论;
(2)如图 2,M 为CD 中点,将 沿 BM 折叠得到 延长BN交AD 于点F.求证:
(3)如图3,过点 C作 于点E,连接BE,求 的值.
1. B 2. C 3. A 4. C 5. D 6. C 7. B 8. D 9. C
10. D 解:设EF 交AB 于点 H,当 FH⊥AB 时,FH 的值最小,EF=2FH 的值也最小.过点C作CG⊥AB 于点G.
∴CG=2 ,∴FH=2
∴线段EF 的最小值为.
11.25 12. AF=CE13.1
16.证明:∵四边形ABCD 是平行四边形,
∴AB∥CD,AB=CD.∵BE=DF,
∴AB+BE=CD+DF,即AE=CF,
∵AB∥CD,∴∠E=∠F,∠OAE=∠OCF,
∴△AOE≌△COF(ASA),∴OE=OF.
17.证明:易证∠EBC=∠EDF=∠DFC,得BE∥DF,又ED∥BF,四边形 DEBF 是平行四边形.
18.证明:(1)∵BE=CF,∴BE+EC=CF+EC,∴BC=EF.又∵AB=DE,AC=DF,∴△ABC≌△DEF(SSS);
(2)∵△ABC≌△DEF,∴∠B=∠DEF,∴AB∥DE.
又∵AB=DE,∴四边形ABED 是平行四边形.
19.解:(1)∵AB=AF,∠BAE=∠FAE,∴AE⊥BF;
(2)易证∠ABC=100°,AB=BE,
∴∠BEA=40°,∠AEC=140°.
20.解:(1)∵四边形ABCD 为平行四边形,
∴AD∥BC,AD=BC.∴∠DAE=∠AEB.
∵AB=AE,∴∠AEB=∠B.
∴∠B=∠DAE,∴△ABC≌△EAD(SAS);
(2)∵△ABC≌△EAD,∴∠AED=∠BAC.
∵AE平分∠DAB,∴∠DAE=∠BAE.
又∵∠DAE=∠AEB,∴∠BAE=∠AEB=∠B,
∴△ABE 为等边三角形,∴∠BAE=60°.
∵∠EAC=25°,∴∠BAC=85°,∴∠AED=85°.
21.解:(1)∵D,E 分别是边AB,AC的中点,
∴DE 是△ABC 的中位线,
(2)连接BD.∵E,F分别是边AB,AD的中点,
∴BD=2EF=3,EF∥BD,∴∠ADB=∠AFE=45°.
∵BC=5,CD=4,∴BC =25,BD +CD =25,
∴∠ADC=∠ADB+∠BDC=135°.
22.解:(1)易得△AOE≌△COF,∴AE=CF.
∵AB=CD,∴BE=DF;
(2)连接CE,过点C作CH⊥AB,交AB 的延长线于点 H.
∵□ABCD,∠ABC=135°,AD=4
∴∠CBH=45°,BC=4
又∵∠H=90°,∴∠BCH=45°,∴CH=BH=4.
设AE=x,则BE=8-x,
∵EF 垂直平分AC,∴CE=AE=x.
∵在Rt△CEH 中,
解得 ∴AE的长为
23.解:(1)∵AE平分∠CAB,CD⊥AE,
∴AC=AD,E 为CD 中点.∵F为BC 的中点,
∴EF 为△BCD 的中位线,.
又∵BD=AB-AD=AB-AC,∴EF= (AB-AC);
(2)延长AE,BC 交于点D,则AB=BD,E 为AD 中点.同
(1)可得
24.解:(1)四边形ABCD 为平行四边形.
∴2a-6=0且a+b-c=0,∴c-b=a=3,
∴BC=c-b=a=3,∴A(0,3),D(d,3),∴AD∥BC.
∵OD 平分∠AOC,∴∠AOD=∠DOC=∠ADO=45°,
∴AD=OA=3,∴AD=BC,∴四边形ABCD为平行四边形;
(2)延长BM,FD 交于点G.可得△BCM≌△GDM,
∴DG=BC=BN,∠G=∠MBC=∠FBM,
∴BF=GF,∴FD=FN;
(3)连接AE,延长CE 交 y轴于点 Q,易得△BOE≌△AQE,得等腰直角
