第十七章《勾股定理》阶段测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十七章《勾股定理》阶段测试卷(含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 111.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 10:22:15 | ||
图片预览



文档简介
第十七章《勾股定理》阶段测试卷
(考试范围:第17.1 解答参考时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
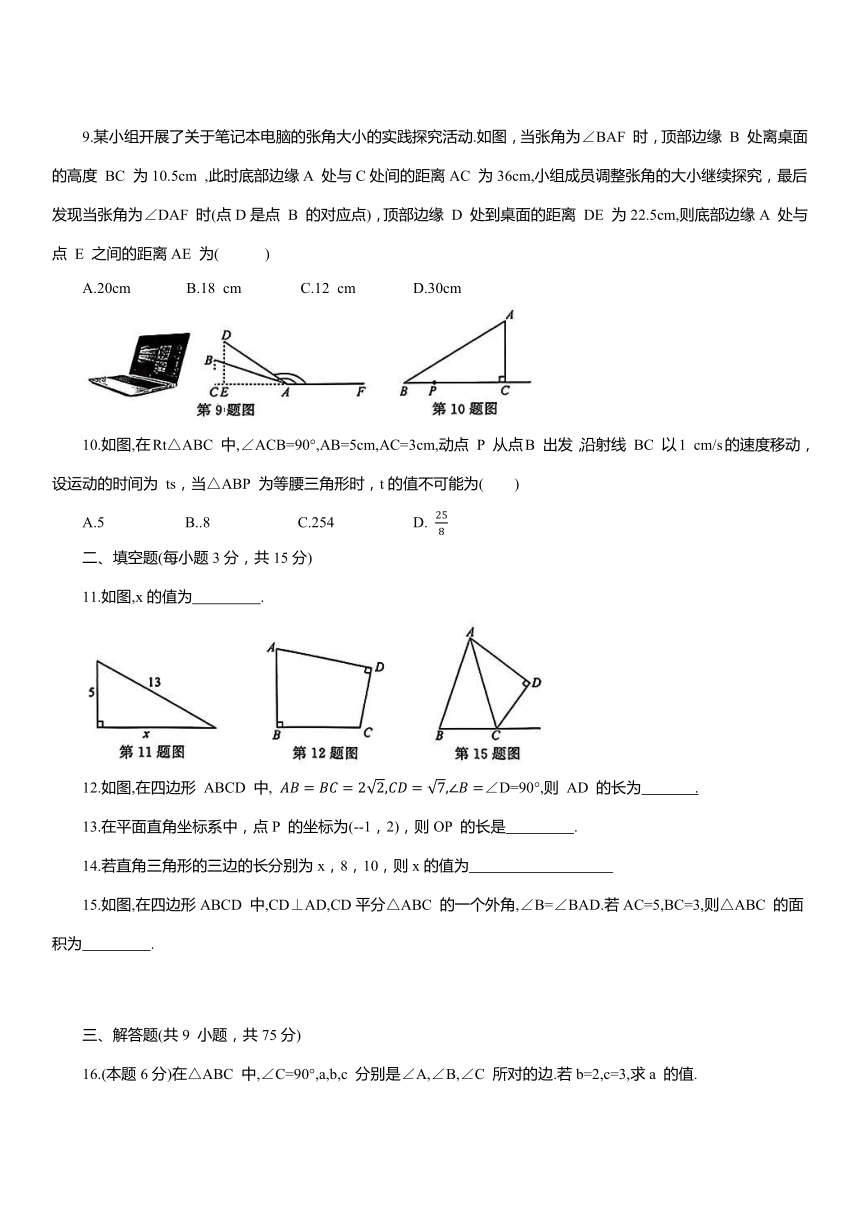
1.如图,在△ABC中,∠C=90°,BC=4,AC=3,则AB 的长为( )
A.2 B.2 C.2 D.5
2.已知直角三角形的两条直角边的长分别为1和2,则斜边的长为( )
A. B. C.3 D.5
3.三个正方形的面积如图所示,则面积为A 的正方形的边长为( )
A.164 B.36 C.8 D.6
4.如图,数轴上点 A 对应的数是-1,点C对应的数是-3,BC⊥AC,垂足为C,且BC=1,以A 为圆心,AB 长为半径画弧,交数轴于点 D,则点 D 表示的数为( )
B. D.
5.如图,在平面直角坐标系中,△OAB 的边OB 落在x 轴上,顶点A落在第一象限.若OA=AB=5,OB=8,则点A 的坐标是( )
A.(8,5) B.(4,5) C.(4,3) D.(3,4)
6.若等边△ABC 的边长为2cm,则△ABC 的面积为( )
D.4 cm
7.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3 B.6 C.8 D.5
8.在Rt△ABC 中,∠C=90°,若AC+BC=14 cm,AB=10 cm,则Rt△ABC 的面积是( )
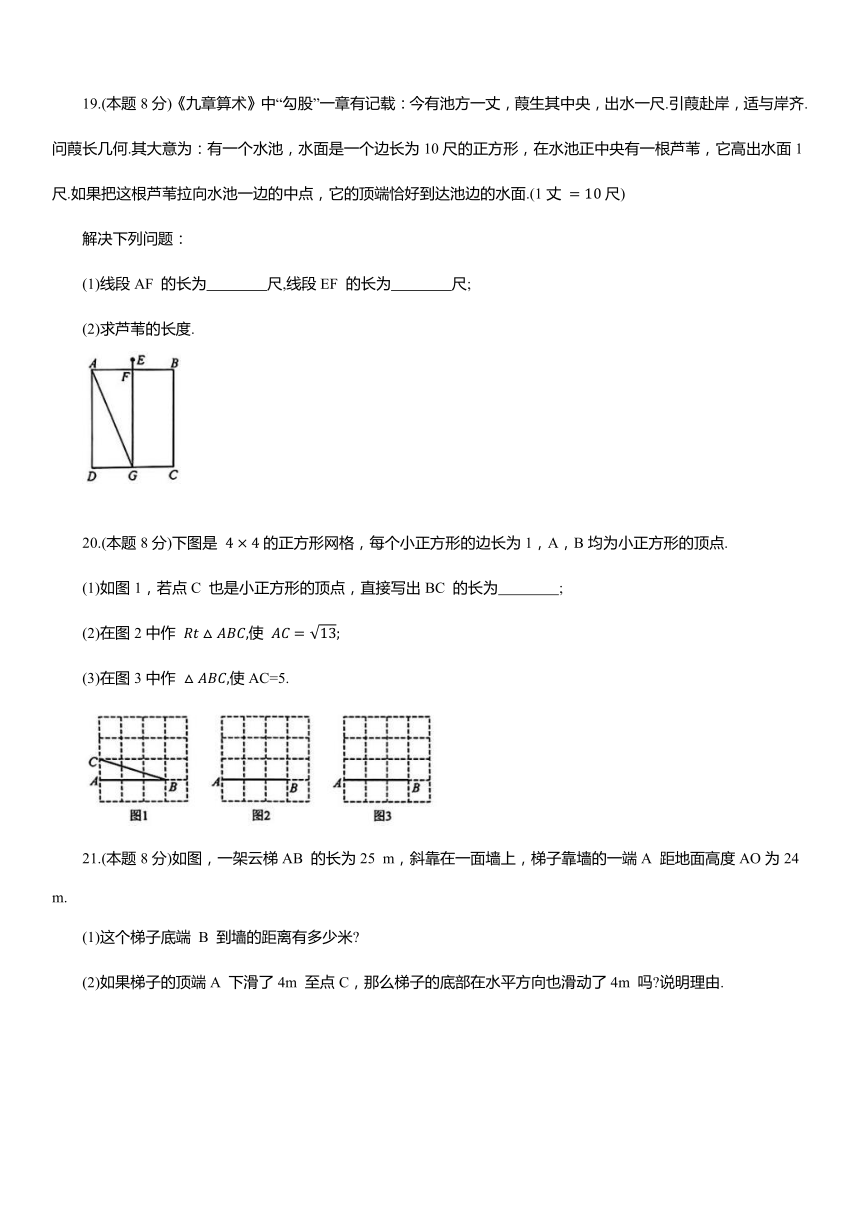
9.某小组开展了关于笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF 时,顶部边缘 B 处离桌面的高度 BC 为10.5cm ,此时底部边缘A 处与C处间的距离AC 为36cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF 时(点D是点 B 的对应点),顶部边缘 D 处到桌面的距离 DE 为22.5cm,则底部边缘A 处与点 E 之间的距离AE 为( )
A.20cm B.18 cm C.12 cm D.30cm
10.如图,在Rt△ABC 中,∠ACB=90°,AB=5cm,AC=3cm,动点 P 从点B 出发,沿射线 BC 以1 cm/s的速度移动,设运动的时间为 ts,当△ABP 为等腰三角形时,t的值不可能为( )
A.5 B..8 C.254 D.
二、填空题(每小题3分,共15分)
11.如图,x的值为 .
12.如图,在四边形 ABCD 中, ∠D=90°,则 AD 的长为 .
13.在平面直角坐标系中,点P 的坐标为(--1,2),则OP 的长是 .
14.若直角三角形的三边的长分别为x,8,10,则x的值为
15.如图,在四边形ABCD 中,CD⊥AD,CD平分△ABC 的一个外角,∠B=∠BAD.若AC=5,BC=3,则△ABC 的面积为 .
三、解答题(共9 小题,共75分)
16.(本题6分)在△ABC 中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 所对的边.若b=2,c=3,求a 的值.
17.(本题6分)如图,在△ABC 中,AB=12,AC=10,BC 边上的高AD=8,求BC边的长.
18.(本题6分)如图,在△ABC 中,AB=AC,∠BAC=120°,D为AC上一点,且AD=DC=2,求AC 的长.
19.(本题8分)《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问葭长几何.其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.(1丈 尺)
解决下列问题:
(1)线段AF 的长为 尺,线段EF 的长为 尺;
(2)求芦苇的长度.
20.(本题8分)下图是 的正方形网格,每个小正方形的边长为1,A,B均为小正方形的顶点.
(1)如图1,若点C 也是小正方形的顶点,直接写出BC 的长为 ;
(2)在图2中作 使
(3)在图3中作 使AC=5.
21.(本题8分)如图,一架云梯AB 的长为25 m,斜靠在一面墙上,梯子靠墙的一端A 距地面高度AO为24 m.
(1)这个梯子底端 B 到墙的距离有多少米
(2)如果梯子的顶端A 下滑了4m 至点C,那么梯子的底部在水平方向也滑动了4m 吗 说明理由.
22.(本题10分)如图,在 中, 垂足为D.
(1)若 求CD的长;
(2)若 ,求CD的长.
23.(本题11分)背景介绍:如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积c 等于四个直角三角形与一个小正方形的面积之和,即 从而得到等式 b) ,化简得结论
方法运用:向常春在2010年构造发现了一个新的证法:把两个全等的Rt△ABC 和 Rt△DEA 如图2放置,其三边长分别为a,b,c,. 显然
(1)请用a,b,c 分别表示出四边形 ABDC,梯形 AEDC, 的面积,再探究这三个图形面积之间的关系,证明勾股定理
方法迁移:
(2)如图3,在 中,AD是BC边上的高, 5,BC=6,设BD=x,求x的值.
24.(本题12分)(1)问题背景:在 中,分别以 AC,AB 为边在 外作等边 等边 求证:
(2)变式迁移:我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形.在(1)中,若 请判断四边形AEBC 是否为勾股四边形 并说明理由;
(3)拓展应用:如图2,在四边形ABCD 中, 直接写出BC 的长为 .
4 第十七章《勾股定理》阶段测试卷
1. D 2. B 3. D 4. C 5. C 6. A 7. B 8. A 9. D
10. C 解:在 Rt△ABC中, ∴BC=4 cm.
①当AB=BP=5cm时,t=5;②当AB=AP 时,BP=2BC=8cm,∴t=8;③当BP=AP 时,设AP=BP =x cm,则CP=(4-x) cm,AC=3cm.在Rt△ACP 中,AP 解得 综上所述,当△ABP 为等腰三角形时,t=5 或t=8 或t= 当 时,△ABP 不是等腰三角形,故选 C.
11.12 12.3 13. 14.6或:
15. 解:延长AD,BC 交于点E,过点 A 作AF⊥BC,垂足为F.易证△CAD≌△CED,∴CE=AC=5,AD=DE.∵∠B=∠BAD,∴AE=BE=BC+CE=8.设CF=x,则 一 解得
16.解:∵
17.解:∵AD⊥BC,
∴BD=4 ,CD=6,∴BC=6+4
18.解:∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵AD=DC,∴∠DAC=∠C=30°,∴∠BAD=90°,
∴AC=AB=2
19.解:(1)由题意,得 尺,EF=1尺,故答案为5,1;
(2)设芦苇长.EG=AG=x尺,则水深FG=(x-1)尺.
在 Rt△AFG中,
答:芦苇长13尺.
20.解:
(2)将点 B 向上平移2个单位长度,得到点 C,图略;
(3)将点 B 向右平移1个单位长度,向上平移3个单位长度,得到点 C,图略.
21.解:(
答:这个梯子底端B 到墙的距离有 7 m;
(2)OC=AO-AC=20(m),CD=AB=25m,
∴DB=OD-OB=8(m),
故如果梯子的顶端下滑了4m,那么梯子的底部在水平方向不是滑4m,而是滑了8m.
22.解:
∵CD·AB=BC·AC=2S△ABC,∴5CD=12,∴CD=
(2)设CD=x,则
∵x>0,∴x=2 ,∴CD=2
23.解:(
S四边形ABDC=S梯形AEDC+S△BED,
(2)在 Rt△ABD 中,由勾股定理,
得
∵BD+CD=BC=6,∴CD=BC-BD=6-x.
在 Rt△ACD 中,由勾股定理,
得
24.解:(1)∵△ACD 与△ABE 均为等边三角形,
∴AE=AB,AD=AC,∠EAB=∠CAD=60°,
∴∠EAC=∠BAD,∴△ABD≌△AEC,∴BD=EC;
(2)四边形AEBC 为勾股四边形.理由:
∵△ACD为等边三角形,∴∠ACD=60°,AC=CD.
∵∠ACB=30°,∴∠DCB=90°,∴BC +CD =BD .
∵EC=BD,AC=CD,∴BC +AC =EC ,
∴四边形AEBC 为勾股四边形;
(3)BC=8.在 AB 的左侧作等边△ABE,连接EC,过点 E作EF⊥BC 交 CB 的延长线于点 F,则 BE =AB =6,∠ABE=60°.
∵∠ABC=60°,∴∠EBF=60°.
∵EF⊥BC,∴∠BEF=30°,
由(1)知
∴BC=FC-FB=11-3=8.
(考试范围:第17.1 解答参考时间:90分钟 满分:120分)
一、选择题(每小题3分,共30分)
1.如图,在△ABC中,∠C=90°,BC=4,AC=3,则AB 的长为( )
A.2 B.2 C.2 D.5
2.已知直角三角形的两条直角边的长分别为1和2,则斜边的长为( )
A. B. C.3 D.5
3.三个正方形的面积如图所示,则面积为A 的正方形的边长为( )
A.164 B.36 C.8 D.6
4.如图,数轴上点 A 对应的数是-1,点C对应的数是-3,BC⊥AC,垂足为C,且BC=1,以A 为圆心,AB 长为半径画弧,交数轴于点 D,则点 D 表示的数为( )
B. D.
5.如图,在平面直角坐标系中,△OAB 的边OB 落在x 轴上,顶点A落在第一象限.若OA=AB=5,OB=8,则点A 的坐标是( )
A.(8,5) B.(4,5) C.(4,3) D.(3,4)
6.若等边△ABC 的边长为2cm,则△ABC 的面积为( )
D.4 cm
7.已知直角三角形的斜边长为10,两直角边的比为3:4,则较短直角边的长为( )
A.3 B.6 C.8 D.5
8.在Rt△ABC 中,∠C=90°,若AC+BC=14 cm,AB=10 cm,则Rt△ABC 的面积是( )
9.某小组开展了关于笔记本电脑的张角大小的实践探究活动.如图,当张角为∠BAF 时,顶部边缘 B 处离桌面的高度 BC 为10.5cm ,此时底部边缘A 处与C处间的距离AC 为36cm,小组成员调整张角的大小继续探究,最后发现当张角为∠DAF 时(点D是点 B 的对应点),顶部边缘 D 处到桌面的距离 DE 为22.5cm,则底部边缘A 处与点 E 之间的距离AE 为( )
A.20cm B.18 cm C.12 cm D.30cm
10.如图,在Rt△ABC 中,∠ACB=90°,AB=5cm,AC=3cm,动点 P 从点B 出发,沿射线 BC 以1 cm/s的速度移动,设运动的时间为 ts,当△ABP 为等腰三角形时,t的值不可能为( )
A.5 B..8 C.254 D.
二、填空题(每小题3分,共15分)
11.如图,x的值为 .
12.如图,在四边形 ABCD 中, ∠D=90°,则 AD 的长为 .
13.在平面直角坐标系中,点P 的坐标为(--1,2),则OP 的长是 .
14.若直角三角形的三边的长分别为x,8,10,则x的值为
15.如图,在四边形ABCD 中,CD⊥AD,CD平分△ABC 的一个外角,∠B=∠BAD.若AC=5,BC=3,则△ABC 的面积为 .
三、解答题(共9 小题,共75分)
16.(本题6分)在△ABC 中,∠C=90°,a,b,c 分别是∠A,∠B,∠C 所对的边.若b=2,c=3,求a 的值.
17.(本题6分)如图,在△ABC 中,AB=12,AC=10,BC 边上的高AD=8,求BC边的长.
18.(本题6分)如图,在△ABC 中,AB=AC,∠BAC=120°,D为AC上一点,且AD=DC=2,求AC 的长.
19.(本题8分)《九章算术》中“勾股”一章有记载:今有池方一丈,葭生其中央,出水一尺.引葭赴岸,适与岸齐.问葭长几何.其大意为:有一个水池,水面是一个边长为10尺的正方形,在水池正中央有一根芦苇,它高出水面1尺.如果把这根芦苇拉向水池一边的中点,它的顶端恰好到达池边的水面.(1丈 尺)
解决下列问题:
(1)线段AF 的长为 尺,线段EF 的长为 尺;
(2)求芦苇的长度.
20.(本题8分)下图是 的正方形网格,每个小正方形的边长为1,A,B均为小正方形的顶点.
(1)如图1,若点C 也是小正方形的顶点,直接写出BC 的长为 ;
(2)在图2中作 使
(3)在图3中作 使AC=5.
21.(本题8分)如图,一架云梯AB 的长为25 m,斜靠在一面墙上,梯子靠墙的一端A 距地面高度AO为24 m.
(1)这个梯子底端 B 到墙的距离有多少米
(2)如果梯子的顶端A 下滑了4m 至点C,那么梯子的底部在水平方向也滑动了4m 吗 说明理由.
22.(本题10分)如图,在 中, 垂足为D.
(1)若 求CD的长;
(2)若 ,求CD的长.
23.(本题11分)背景介绍:如图1是著名的赵爽弦图,由四个全等的直角三角形拼成,用它可以证明勾股定理,思路是大正方形的面积c 等于四个直角三角形与一个小正方形的面积之和,即 从而得到等式 b) ,化简得结论
方法运用:向常春在2010年构造发现了一个新的证法:把两个全等的Rt△ABC 和 Rt△DEA 如图2放置,其三边长分别为a,b,c,. 显然
(1)请用a,b,c 分别表示出四边形 ABDC,梯形 AEDC, 的面积,再探究这三个图形面积之间的关系,证明勾股定理
方法迁移:
(2)如图3,在 中,AD是BC边上的高, 5,BC=6,设BD=x,求x的值.
24.(本题12分)(1)问题背景:在 中,分别以 AC,AB 为边在 外作等边 等边 求证:
(2)变式迁移:我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形.在(1)中,若 请判断四边形AEBC 是否为勾股四边形 并说明理由;
(3)拓展应用:如图2,在四边形ABCD 中, 直接写出BC 的长为 .
4 第十七章《勾股定理》阶段测试卷
1. D 2. B 3. D 4. C 5. C 6. A 7. B 8. A 9. D
10. C 解:在 Rt△ABC中, ∴BC=4 cm.
①当AB=BP=5cm时,t=5;②当AB=AP 时,BP=2BC=8cm,∴t=8;③当BP=AP 时,设AP=BP =x cm,则CP=(4-x) cm,AC=3cm.在Rt△ACP 中,AP 解得 综上所述,当△ABP 为等腰三角形时,t=5 或t=8 或t= 当 时,△ABP 不是等腰三角形,故选 C.
11.12 12.3 13. 14.6或:
15. 解:延长AD,BC 交于点E,过点 A 作AF⊥BC,垂足为F.易证△CAD≌△CED,∴CE=AC=5,AD=DE.∵∠B=∠BAD,∴AE=BE=BC+CE=8.设CF=x,则 一 解得
16.解:∵
17.解:∵AD⊥BC,
∴BD=4 ,CD=6,∴BC=6+4
18.解:∵AB=AC,∠BAC=120°,∴∠B=∠C=30°.
∵AD=DC,∴∠DAC=∠C=30°,∴∠BAD=90°,
∴AC=AB=2
19.解:(1)由题意,得 尺,EF=1尺,故答案为5,1;
(2)设芦苇长.EG=AG=x尺,则水深FG=(x-1)尺.
在 Rt△AFG中,
答:芦苇长13尺.
20.解:
(2)将点 B 向上平移2个单位长度,得到点 C,图略;
(3)将点 B 向右平移1个单位长度,向上平移3个单位长度,得到点 C,图略.
21.解:(
答:这个梯子底端B 到墙的距离有 7 m;
(2)OC=AO-AC=20(m),CD=AB=25m,
∴DB=OD-OB=8(m),
故如果梯子的顶端下滑了4m,那么梯子的底部在水平方向不是滑4m,而是滑了8m.
22.解:
∵CD·AB=BC·AC=2S△ABC,∴5CD=12,∴CD=
(2)设CD=x,则
∵x>0,∴x=2 ,∴CD=2
23.解:(
S四边形ABDC=S梯形AEDC+S△BED,
(2)在 Rt△ABD 中,由勾股定理,
得
∵BD+CD=BC=6,∴CD=BC-BD=6-x.
在 Rt△ACD 中,由勾股定理,
得
24.解:(1)∵△ACD 与△ABE 均为等边三角形,
∴AE=AB,AD=AC,∠EAB=∠CAD=60°,
∴∠EAC=∠BAD,∴△ABD≌△AEC,∴BD=EC;
(2)四边形AEBC 为勾股四边形.理由:
∵△ACD为等边三角形,∴∠ACD=60°,AC=CD.
∵∠ACB=30°,∴∠DCB=90°,∴BC +CD =BD .
∵EC=BD,AC=CD,∴BC +AC =EC ,
∴四边形AEBC 为勾股四边形;
(3)BC=8.在 AB 的左侧作等边△ABE,连接EC,过点 E作EF⊥BC 交 CB 的延长线于点 F,则 BE =AB =6,∠ABE=60°.
∵∠ABC=60°,∴∠EBF=60°.
∵EF⊥BC,∴∠BEF=30°,
由(1)知
∴BC=FC-FB=11-3=8.
