第十二章 数据的收集、整理与描述 章末复习 教案 人教版(2024)数学七年级下册
文档属性
| 名称 | 第十二章 数据的收集、整理与描述 章末复习 教案 人教版(2024)数学七年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 797.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:17:30 | ||
图片预览




文档简介
第十二章 数据的收集、整理与描述
章末复习
1.掌握简单的收集与整理数据的方法,了解全面调查、抽样调查、总体、个体、样本、样本容量、简单随机抽样等概念.
2.掌握画频数分布直方图和趋势图的步骤,会画频数分布直方图和趋势图,并能从图中读取正确信息.
3.能选择适当的统计图描述数据,并能从统计图中获取有用的信息,作出合理的判断和预测.
利用表格、条形图、扇形图、折线图、直方图、趋势图等多种方式整理和分析数据.
对整理的数据进行科学的分析.
复习导入
请你带着下面的问题,复习一下全章的内容吧.
1.什么是全面调查和抽样调查?它们各有什么优缺点?哪些情况下宜用全面调查?哪些情况下宜用抽样调查?
2.为什么抽样调查可以作为了解总体的方法?为了使样本对总体有较好的代表性,抽样时需要注意什么?
3.简单随机抽样有什么特点?用简单随机抽样抽出的样本是否一定具有代表性?请举例说明.
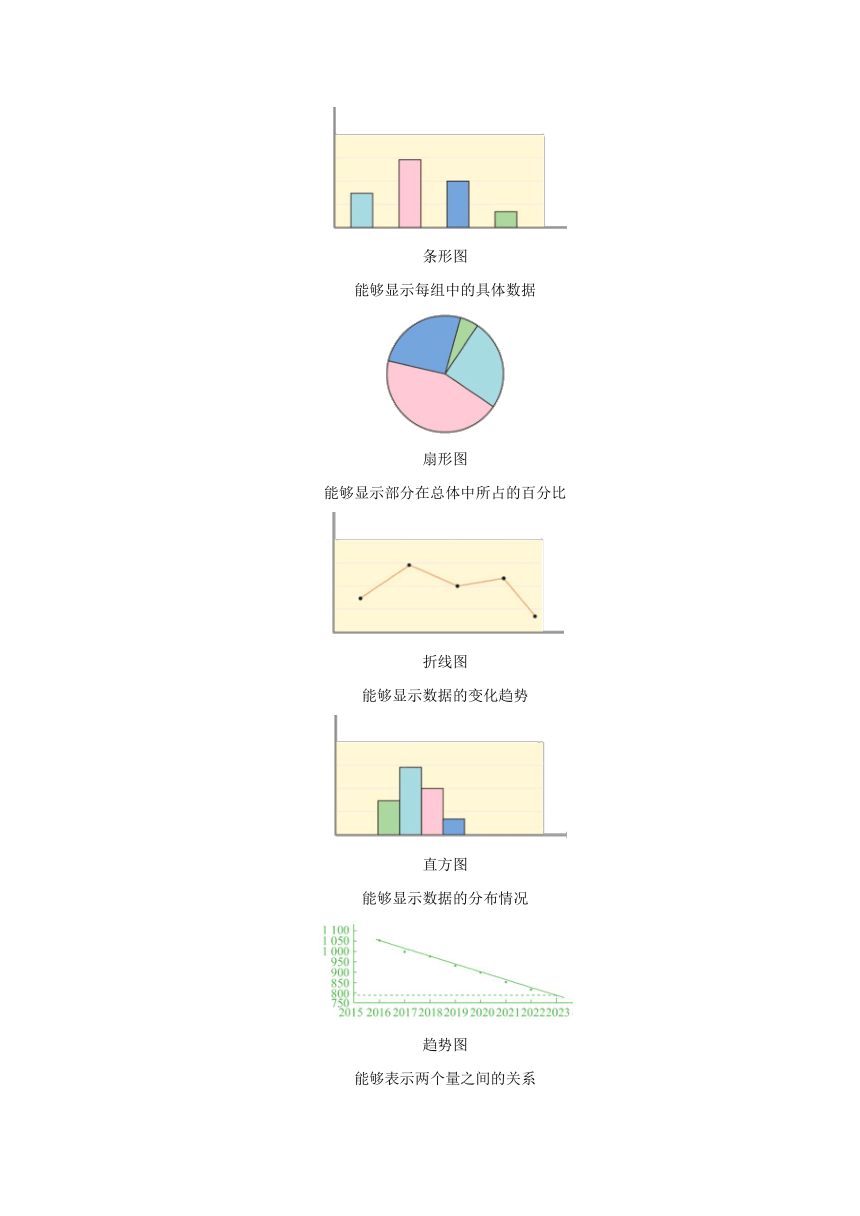
4.扇形图、条形图、折线图、直方图和趋势图在描述数据方面各有什么特点?请举例说明如何根据问题的需要选取恰当的统计图表示数据.
条形图
能够显示每组中的具体数据
扇形图
能够显示部分在总体中所占的百分比
折线图
能够显示数据的变化趋势
直方图
能够显示数据的分布情况
趋势图
能够表示两个量之间的关系
【设计意图】以问题串的形式创设情境,引导学生复习回顾已学知识点,通过学生回答,检查学生对知识的掌握情况,加深学生对知识的理解,提高学生灵活运用知识的能力.
要点复习
考点一 数据收集方式的选择
【例1】下面获取数据的方法不正确的是( ).
A.了解我们班同学的身高用测量方法
B.快速了解历史资料用观察方法
C.抛硬币看正反面的次数用试验法
D.了解全班同学最喜爱的体育活动采用问卷调查的方法
【师生活动】小组讨论得出答案,教师给出正确答案并引导学生归纳知识点.
【答案】B
【解析】快速了解历史资料应该采用查阅资料或上网搜索的方法.
【归纳】收集数据的方式有哪些?应如何选择?
收集数据的方式有问卷调查、访谈、查阅资料、实地调查、试验、上网搜索等.选择调查方式时,要根据具体问题选择合适的调查方式,同时也要考虑调查的可操作性.
【设计意图】巩固学生对收集数据的方式的掌握情况.
【跟踪训练1】某同学想了解学校门前10分钟内通行的车辆数量,他应采取的收集数据的方法为( ).
A.査阅资料 B.试验 C.问卷调查 D.观察
【答案】D
【解析】要了解学校门前10分钟内通行的车辆数量,调查范围比较小且容易调查,所以直接观察即可.
考点二 全面调查与抽样调查的选用
【例2】以下问题不适合全面调查的是( ).
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】C
【解析】选项A:班级学生人数较少,适合全面调查;
选项B:某中学在职教师身体健康状况适合全面调查;
选项C:调查全国中小学生课外阅读情况,人数众多,不适合全面调查;
选项D:某校篮球队员的身高适合全面调查.
【归纳】如何正确地选择全面调查或抽样调查?
选择全面调查还是抽样调查要根据所要考察的对象的特征灵活选用.一般来说,对于具有破坏性的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查、事关重大的调查、调查对象数量较少的调查往往选用全面调查.
【设计意图】让学生进一步理解和掌握全面调查与抽样调查的区别.
【跟踪训练2】下列调查中,适宜采用全面调查方式的是( ).
A.对我国初中学生视力状况的调查
B.对量子科学通信卫星上某种零部件的检查
C.对一批节能灯管使用寿命的调查
D.对某节目收视率的调查
【答案】B
【解析】选项A:对我国初中学生视力状况的调查,工作量大,适合抽样调查;
选项B:对量子科学通信卫星上某种零部件的检查,虽然工作量较大,但要求高,不能有任何闪失,必须进行全面调查;
选项C:对一批节能灯管使用寿命的调查,具有破坏性,所以适合抽样调查;
选项D:对某节目收视率的调查,工作量大,且不需要很精确的结果,适合抽样调查.
考点三 总体、个体、样本和样本容量
【例3】为了解某校学生的体重情况,随机抽取45名学生的体重(单位:kg)记录如下:
48,48,42,50,61,44,43,51,46,46,46,51,50,45,52,54,51,57,55,
48,49,48,53,48,56,55,57,42,54,49,47,60,51,51,44,41,49,53,
52,49,61,58,52,54,50.
这个问题中的总体、个体、样本分别是什么?
【师生活动】小组讨论得出答案,教师给出正确答案并引导学生归纳知识点.
【答案】解:总体是该校学生的体重,个体是该校每名学生的体重,样本是被抽取的45名学生的体重(或总体是该校学生,个体是该校的每名学生,样本是被抽取的45名学生).
【归纳】怎样区分总体、个体和样本?样本容量的大小是如何确定的?
(1)总体包括所有个体,样本只包括一部分个体,样本是总体的一部分,总体可以有多个样本;
(2)样本容量的大小要根据实际情况来确定,样本容量越大,样本的特征越接近总体的特征.注意样本容量是个数,不能带单位.
【设计意图】检验学生对总体、个体、样本和样本容量等概念的理解与掌握情况.
【跟踪训练3】为纪念中国人民抗日战争的胜利,9月3日被确定为抗日战争胜利纪念日,某校为了了解学生对“抗日战争”的知晓情况,从全校6 000名学生中,随机抽取了120名学生进行调查,在这次调查中( ).
A.120名学生是总体
B.所抽取的每一名学生对“抗日战争”的知晓情况是总体的一个样本
C.120名是样本容量
D.所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本
【答案】D
【解析】全校6 000名学生对“抗日战争”的知晓情况是总体,所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本(或全校6 000名学生是总体,所抽取的120名学生是总体的一个样本),故A选项错误,D选项正确;
所抽取的每一名学生对“抗日战争”的知晓情况是总体的一个个体,故B选项错误;
样本容量是120,故C选项错误.故选D.
考点四 频数分布直方图及其应用
【例4】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民一周的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了统计表和如图所示的频数分布直方图.
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 45%
9 22.5%
1 600≤x<1 800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全统计表;
(2)补全频数分布直方图;
(3)请你估计,该居民小区家庭属于中等收入(一周收入大于等于1 000元而不足1 600元)的大约有多少户?
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】解:(1)补全的统计表如下:
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 18 45%
1 200≤x<1 400 9 22.5%
1 400≤x<1 600 3 7.5%
1 600≤x<1 800 2 5%
合计 40 100%
(2)补全的频数分布直方图如图所示:
(3)18+9+3=30,450×≈338(户).
故该居民小区家庭属于中等收入(一周收入大于等于1 000元而不足1 600元)的大约有338户.
【设计意图】检验学生对频数分布表和频数分布直方图的掌握情况.
【跟踪训练4】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查.利用所得数据绘成统计图表:
频数分布表
身高分组 频数 百分比
x<155 5 10%
155≤x<160 a 20%
160≤x<165 15 30%
165≤x<170 14 b
x≥170 6 12%
总计 100%
频数分布直方图
(1)填空:a=_______,b=_______;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,则身高不低于165 cm的学生大约有多少人?
【答案】解:(1)求a:
方法1:由统计表看出155≤x<160的人数a应是x<155的人数的2倍,即a=10.
方法2:总人数为5÷10%=50,50×20%=10.
求b:
b=100%-10%-20%-30%-12%=28%.
(2)根据a=10,补全直方图如图所示.
频数分布直方图
(3)600×(28%+12%)=240(人).
答:身高不低于165 cm的学生大约有240人.
考点五 趋势图及其应用
【例5】在某种产品的表面进行腐蚀刻度线试验,得到腐蚀时间x(单位:min)与腐蚀深度y(单位:μm)之间的样本数据如下表.
x/min 5 10 15 20 30 40 50 60 70 90
y/μm 6 10 11 13 16 17 19 23 25 29
(1)请用统计图描述腐蚀深度随腐蚀时间的变化趋势.
(2)请你根据(1)中所作的统计图预测当腐蚀时间为100 min时的腐蚀深度.
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】解:(1)作出趋势图如图所示.
(2)预测当腐蚀时间为100 min时的腐蚀深度为31 μm.
【设计意图】检验学生对趋势图的掌握情况.
【跟踪训练5】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如下表所示.
单价/元 8 8.2 8.4 8.6 8.8 9
销售量/件 6 10 11 13 16 17
(1)用趋势图描述销售量与单价之间的关系.
(2)根据你作的趋势图,预测单价为9.2元时的销售量.
【答案】解:(1)画出趋势图如图所示.
(2)根据(1)中所作趋势图可预测,单价为9.2元时的销售量约为65件.
考点六 统计图的综合应用
【例6】某校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1 600名学生每人都参加且只参加了其中一个社团的活动.校团委从这1 600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图①②所示的不完整的统计图,请根据统计图完成下列问题:
被调查学生参加各社团人数条形图
被调查学生参加各社团人数占被调查学生总人数的百分比扇形图
(1)参加本次调查有_______名学生,根据调查数据分析,全校约有_______名学生参加了音乐社团;
(2)请你补全条形图.
【师生活动】学生代表作答,教师补充并讲解知识点.
【答案】解:(1)参加本次调查的学生有24÷10%=240(名),
则参加“书法”社团的人数为240×15%=36,
参加“舞蹈”社团的人数为240×20%=48,
所以参加“音乐”社团的人数为240-36-72-48-24=60,
全校参加音乐社团的学生人数大约为1600×=400.
故答案为:240,400.
(2)补全的条形图如图所示.
被调查学生参加各社团人数条形图
【归纳】怎样补全统计图?
题干给我们的统计图表,一般都是不完整的,需要进行补全.补全频数分布直方图(或条形图)需根据各组之和等于数据总和,补全扇形图需根据各部分所占百分比之和为1.
【设计意图】锻炼学生解决统计图相关的综合问题的能力.
【跟踪训练6】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如图①②所示的两幅不完整的统计图.
(1)“从来不管”的问卷有_______份,在扇形图中“严加干涉”的问卷对应的扇形圆心角为________°;
(2)请把条形图补充完整;
(3)若该校共有学生2 000名,请估计,该校对手机问题“严加干涉”的家长有多少人?
【答案】解:(1)“从来不管”的问卷有100×25%=25(份),
在扇形图中“严加干涉”的问卷对应的圆心角为360°×20%=72°,
故答案为:25,72.
(2)由(1)知,“从来不管”的问卷有25份,
则“严加干涉”的问卷有100-25-55=20(份).
补全的条形图如下图所示.
(3)2 000×20%=400(人),
所以估计该校对手机问题“严加干涉”的家长有400人.
课堂小结
课后任务
完成教材第184页复习题12第1~7题.
章末复习
1.掌握简单的收集与整理数据的方法,了解全面调查、抽样调查、总体、个体、样本、样本容量、简单随机抽样等概念.
2.掌握画频数分布直方图和趋势图的步骤,会画频数分布直方图和趋势图,并能从图中读取正确信息.
3.能选择适当的统计图描述数据,并能从统计图中获取有用的信息,作出合理的判断和预测.
利用表格、条形图、扇形图、折线图、直方图、趋势图等多种方式整理和分析数据.
对整理的数据进行科学的分析.
复习导入
请你带着下面的问题,复习一下全章的内容吧.
1.什么是全面调查和抽样调查?它们各有什么优缺点?哪些情况下宜用全面调查?哪些情况下宜用抽样调查?
2.为什么抽样调查可以作为了解总体的方法?为了使样本对总体有较好的代表性,抽样时需要注意什么?
3.简单随机抽样有什么特点?用简单随机抽样抽出的样本是否一定具有代表性?请举例说明.
4.扇形图、条形图、折线图、直方图和趋势图在描述数据方面各有什么特点?请举例说明如何根据问题的需要选取恰当的统计图表示数据.
条形图
能够显示每组中的具体数据
扇形图
能够显示部分在总体中所占的百分比
折线图
能够显示数据的变化趋势
直方图
能够显示数据的分布情况
趋势图
能够表示两个量之间的关系
【设计意图】以问题串的形式创设情境,引导学生复习回顾已学知识点,通过学生回答,检查学生对知识的掌握情况,加深学生对知识的理解,提高学生灵活运用知识的能力.
要点复习
考点一 数据收集方式的选择
【例1】下面获取数据的方法不正确的是( ).
A.了解我们班同学的身高用测量方法
B.快速了解历史资料用观察方法
C.抛硬币看正反面的次数用试验法
D.了解全班同学最喜爱的体育活动采用问卷调查的方法
【师生活动】小组讨论得出答案,教师给出正确答案并引导学生归纳知识点.
【答案】B
【解析】快速了解历史资料应该采用查阅资料或上网搜索的方法.
【归纳】收集数据的方式有哪些?应如何选择?
收集数据的方式有问卷调查、访谈、查阅资料、实地调查、试验、上网搜索等.选择调查方式时,要根据具体问题选择合适的调查方式,同时也要考虑调查的可操作性.
【设计意图】巩固学生对收集数据的方式的掌握情况.
【跟踪训练1】某同学想了解学校门前10分钟内通行的车辆数量,他应采取的收集数据的方法为( ).
A.査阅资料 B.试验 C.问卷调查 D.观察
【答案】D
【解析】要了解学校门前10分钟内通行的车辆数量,调查范围比较小且容易调查,所以直接观察即可.
考点二 全面调查与抽样调查的选用
【例2】以下问题不适合全面调查的是( ).
A.调查某班学生每周课前预习的时间
B.调查某中学在职教师的身体健康状况
C.调查全国中小学生课外阅读情况
D.调查某校篮球队员的身高
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】C
【解析】选项A:班级学生人数较少,适合全面调查;
选项B:某中学在职教师身体健康状况适合全面调查;
选项C:调查全国中小学生课外阅读情况,人数众多,不适合全面调查;
选项D:某校篮球队员的身高适合全面调查.
【归纳】如何正确地选择全面调查或抽样调查?
选择全面调查还是抽样调查要根据所要考察的对象的特征灵活选用.一般来说,对于具有破坏性的调查、无法进行全面调查、全面调查的意义或价值不大时,应选择抽样调查;对于精确度要求高的调查、事关重大的调查、调查对象数量较少的调查往往选用全面调查.
【设计意图】让学生进一步理解和掌握全面调查与抽样调查的区别.
【跟踪训练2】下列调查中,适宜采用全面调查方式的是( ).
A.对我国初中学生视力状况的调查
B.对量子科学通信卫星上某种零部件的检查
C.对一批节能灯管使用寿命的调查
D.对某节目收视率的调查
【答案】B
【解析】选项A:对我国初中学生视力状况的调查,工作量大,适合抽样调查;
选项B:对量子科学通信卫星上某种零部件的检查,虽然工作量较大,但要求高,不能有任何闪失,必须进行全面调查;
选项C:对一批节能灯管使用寿命的调查,具有破坏性,所以适合抽样调查;
选项D:对某节目收视率的调查,工作量大,且不需要很精确的结果,适合抽样调查.
考点三 总体、个体、样本和样本容量
【例3】为了解某校学生的体重情况,随机抽取45名学生的体重(单位:kg)记录如下:
48,48,42,50,61,44,43,51,46,46,46,51,50,45,52,54,51,57,55,
48,49,48,53,48,56,55,57,42,54,49,47,60,51,51,44,41,49,53,
52,49,61,58,52,54,50.
这个问题中的总体、个体、样本分别是什么?
【师生活动】小组讨论得出答案,教师给出正确答案并引导学生归纳知识点.
【答案】解:总体是该校学生的体重,个体是该校每名学生的体重,样本是被抽取的45名学生的体重(或总体是该校学生,个体是该校的每名学生,样本是被抽取的45名学生).
【归纳】怎样区分总体、个体和样本?样本容量的大小是如何确定的?
(1)总体包括所有个体,样本只包括一部分个体,样本是总体的一部分,总体可以有多个样本;
(2)样本容量的大小要根据实际情况来确定,样本容量越大,样本的特征越接近总体的特征.注意样本容量是个数,不能带单位.
【设计意图】检验学生对总体、个体、样本和样本容量等概念的理解与掌握情况.
【跟踪训练3】为纪念中国人民抗日战争的胜利,9月3日被确定为抗日战争胜利纪念日,某校为了了解学生对“抗日战争”的知晓情况,从全校6 000名学生中,随机抽取了120名学生进行调查,在这次调查中( ).
A.120名学生是总体
B.所抽取的每一名学生对“抗日战争”的知晓情况是总体的一个样本
C.120名是样本容量
D.所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本
【答案】D
【解析】全校6 000名学生对“抗日战争”的知晓情况是总体,所抽取的120名学生对“抗日战争”的知晓情况是总体的一个样本(或全校6 000名学生是总体,所抽取的120名学生是总体的一个样本),故A选项错误,D选项正确;
所抽取的每一名学生对“抗日战争”的知晓情况是总体的一个个体,故B选项错误;
样本容量是120,故C选项错误.故选D.
考点四 频数分布直方图及其应用
【例4】小龙在学校组织的社会调查活动中负责了解他所居住的小区450户居民一周的家庭收入情况.他从中随机调查了40户居民家庭收入情况(收入取整数,单位:元),并绘制了统计表和如图所示的频数分布直方图.
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 45%
9 22.5%
1 600≤x<1 800 2
合计 40 100%
根据以上提供的信息,解答下列问题:
(1)补全统计表;
(2)补全频数分布直方图;
(3)请你估计,该居民小区家庭属于中等收入(一周收入大于等于1 000元而不足1 600元)的大约有多少户?
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】解:(1)补全的统计表如下:
分组 频数 百分比
600≤x<800 2 5%
800≤x<1 000 6 15%
1 000≤x<1 200 18 45%
1 200≤x<1 400 9 22.5%
1 400≤x<1 600 3 7.5%
1 600≤x<1 800 2 5%
合计 40 100%
(2)补全的频数分布直方图如图所示:
(3)18+9+3=30,450×≈338(户).
故该居民小区家庭属于中等收入(一周收入大于等于1 000元而不足1 600元)的大约有338户.
【设计意图】检验学生对频数分布表和频数分布直方图的掌握情况.
【跟踪训练4】为了解某校九年级学生的身高情况,随机抽取部分学生的身高进行调查.利用所得数据绘成统计图表:
频数分布表
身高分组 频数 百分比
x<155 5 10%
155≤x<160 a 20%
160≤x<165 15 30%
165≤x<170 14 b
x≥170 6 12%
总计 100%
频数分布直方图
(1)填空:a=_______,b=_______;
(2)补全频数分布直方图;
(3)该校九年级共有600名学生,则身高不低于165 cm的学生大约有多少人?
【答案】解:(1)求a:
方法1:由统计表看出155≤x<160的人数a应是x<155的人数的2倍,即a=10.
方法2:总人数为5÷10%=50,50×20%=10.
求b:
b=100%-10%-20%-30%-12%=28%.
(2)根据a=10,补全直方图如图所示.
频数分布直方图
(3)600×(28%+12%)=240(人).
答:身高不低于165 cm的学生大约有240人.
考点五 趋势图及其应用
【例5】在某种产品的表面进行腐蚀刻度线试验,得到腐蚀时间x(单位:min)与腐蚀深度y(单位:μm)之间的样本数据如下表.
x/min 5 10 15 20 30 40 50 60 70 90
y/μm 6 10 11 13 16 17 19 23 25 29
(1)请用统计图描述腐蚀深度随腐蚀时间的变化趋势.
(2)请你根据(1)中所作的统计图预测当腐蚀时间为100 min时的腐蚀深度.
【师生活动】学生作答,教师纠正并讲解知识点.
【答案】解:(1)作出趋势图如图所示.
(2)预测当腐蚀时间为100 min时的腐蚀深度为31 μm.
【设计意图】检验学生对趋势图的掌握情况.
【跟踪训练5】某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到数据如下表所示.
单价/元 8 8.2 8.4 8.6 8.8 9
销售量/件 6 10 11 13 16 17
(1)用趋势图描述销售量与单价之间的关系.
(2)根据你作的趋势图,预测单价为9.2元时的销售量.
【答案】解:(1)画出趋势图如图所示.
(2)根据(1)中所作趋势图可预测,单价为9.2元时的销售量约为65件.
考点六 统计图的综合应用
【例6】某校组建了书法、音乐、美术、舞蹈、演讲五个社团,全校1 600名学生每人都参加且只参加了其中一个社团的活动.校团委从这1 600名学生中随机选取部分学生进行了参加活动情况的调查,并将调查结果制成了如图①②所示的不完整的统计图,请根据统计图完成下列问题:
被调查学生参加各社团人数条形图
被调查学生参加各社团人数占被调查学生总人数的百分比扇形图
(1)参加本次调查有_______名学生,根据调查数据分析,全校约有_______名学生参加了音乐社团;
(2)请你补全条形图.
【师生活动】学生代表作答,教师补充并讲解知识点.
【答案】解:(1)参加本次调查的学生有24÷10%=240(名),
则参加“书法”社团的人数为240×15%=36,
参加“舞蹈”社团的人数为240×20%=48,
所以参加“音乐”社团的人数为240-36-72-48-24=60,
全校参加音乐社团的学生人数大约为1600×=400.
故答案为:240,400.
(2)补全的条形图如图所示.
被调查学生参加各社团人数条形图
【归纳】怎样补全统计图?
题干给我们的统计图表,一般都是不完整的,需要进行补全.补全频数分布直方图(或条形图)需根据各组之和等于数据总和,补全扇形图需根据各部分所占百分比之和为1.
【设计意图】锻炼学生解决统计图相关的综合问题的能力.
【跟踪训练6】某校为了了解学生家长对孩子用手机的态度问题,随机抽取了100名家长进行问卷调查,每位学生家长只有一份问卷,且每份问卷仅表明一种态度(这100名家长的问卷真实有效),将这100份问卷进行回收整理后,绘制了如图①②所示的两幅不完整的统计图.
(1)“从来不管”的问卷有_______份,在扇形图中“严加干涉”的问卷对应的扇形圆心角为________°;
(2)请把条形图补充完整;
(3)若该校共有学生2 000名,请估计,该校对手机问题“严加干涉”的家长有多少人?
【答案】解:(1)“从来不管”的问卷有100×25%=25(份),
在扇形图中“严加干涉”的问卷对应的圆心角为360°×20%=72°,
故答案为:25,72.
(2)由(1)知,“从来不管”的问卷有25份,
则“严加干涉”的问卷有100-25-55=20(份).
补全的条形图如下图所示.
(3)2 000×20%=400(人),
所以估计该校对手机问题“严加干涉”的家长有400人.
课堂小结
课后任务
完成教材第184页复习题12第1~7题.
同课章节目录
