第12章 数据的收集、整理与描述 章综合复习 课件(共28张PPT)人教版(2024)数学七年级下册
文档属性
| 名称 | 第12章 数据的收集、整理与描述 章综合复习 课件(共28张PPT)人教版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 7.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:28:48 | ||
图片预览








文档简介
(共28张PPT)
章综合复习
【第十二章 数据的收集、整理与描述】
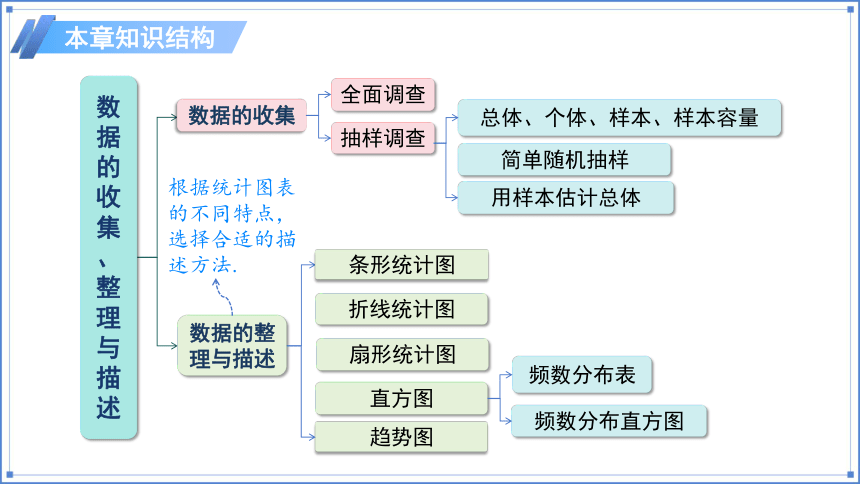
数据的收集
、整理与描述
全面调查
数据的收集
抽样调查
折线统计图
数据的整理与描述
条形统计图
趋势图
扇形统计图
直方图
频数分布表
频数分布直方图
总体、个体、样本、样本容量
用样本估计总体
简单随机抽样
根据统计图表的不同特点,选择合适的描述方法.
全面调查:考察全体对象的调查叫作全面调查.
概念
注:总体是由个体组成的,个体是总体中的一个.
要点
全面调查
总体与个体:要考察的全体对象称为总体,组成总体的每一个调查对象称为个体.
适用范围:一般地,当调查的范围小、调查不具有破坏性、数据要求准确全面时,采用全面调查.
优点:结果准确,有利于全面了解数据;
缺点:花费时间长,消耗的人力、物力大,易受条件限制,不适用于具有破坏性的调查.
概念
抽样调查
抽样调查:只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种方法称为抽样调查.
适用范围:一般地,当调查具有破坏性、调查范围大、受条件限制无法进行全面调查或全面调查的意义、价值不大时,采用抽样调查.
优点:调查范围小,省时省力;
缺点:结果的准确程度受抽取样本的影响,不能全面了解数据.
要点
方法:简单随机抽样.
从总体中被抽取调查的那些个体构成总体的一个样本,样本中包含的个体的数目称为样本容量.
概念
要点
样本
(1)总体包含所有个体,样本只包括所抽取的个体;
(2)样本是总体的一部分,一个总体可以有多个样本;
(3)样本容量是样本中所含个体的个数,不是调查对象,而且没有单位.
概念
用样本估计总体
简单随机抽样
简单随机抽样:在抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法称为简单随机抽样.
(1)一般情况下,样本容量越大,样本对总体的估计越准确,在解决实际问题中,要根据具体情况确定样本容量的大小;
(2)抽取的样本在一定程度上能够反映总体,为了使样本能较好地反映总体情况,在选取样本时,除了样本容量要合适,抽取的样本也要具有一定的代表性.
注:当总体中的个体数较多时,常采用简单随机抽样来进行调查.
表示
要点
扇形图
扇形图用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
(1)特点:扇形图可以直观地反映各部分占整体的百分比,但不能清楚地表明每一个项目的具体数目;
(2)扇形图中,各部分占整体的百分比之和为100%或1.
(3)在扇形图中,用圆代表整体,但圆的大小与具体的数量的多少无关.
扇形图中圆心角的度数:在扇形图中,每部分所对应的扇形圆心角的度数=该部分占总体的百分比×360°.即扇形面积占圆面积的百分比.
方法
统计图的选择
(1)需要表达的数据是分散的,并且需要清晰地表示出各组实际数据,选择条形图较为适宜;
(2)需要表达各组数据占整体的百分比,选择扇形图较为适宜;
(3)需要清晰地显示各组数据在一段时期内的变化,或分析数据的变化趋势,选择折线图较为适宜.
注意
在同一统计图中,为了表示两组或两组以上的数据,用于不同数据之间的比较,可绘制复合折线图和复合条形图.
概念
直方图
注意
是一个数值,没有单位.
把数据分为若干组:
组距:每一组两个端点之间的距离叫组距;
组数:把数分成若干组,分成组的个数叫组数;频数:落在各小组内的数据的个数叫该组的频数;
频率:频数占总数的百分比叫频率,频率=
当数据在100个以内时,根据数据的多少通常分成5-12组.
一般地,组数= (向下取整)+1
表示方法
直方图
意义
频数分布直方图是一种特殊的条形图,它将统计对象的数据进行了分组,画在横轴上,对于等距分组的频数分布直方图,通常纵轴表示各组数据的频数.(高表示相应各组数据的频数,即各小长方形的高之比等于所对应的各组数据的频数之比 )
直方图是条形图,但条形图不是直方图
频数分布直方图由横轴、纵轴、小长方形三部分构成;横轴表示分组情况,纵轴表示频数与组距的比值.
画法
直方图
绘制频数分布直方图的步骤:
(1)计算最大值与最小值的差;
(2)决定组距和组数;
(3)列频数分布表;
(4)画频数分布直方图.
概念
趋势图
趋势图:用一条线(直线或曲线)来描述一个量与另一个量之间关系的统计图,叫作趋势图.
特点
趋势图比较清楚地表示了两个量之间的关系,有利于根据一个量的变化,预测另一个量的变化趋势.
通过“数据的分析”的学习,我们知道了统计调査活动要经历的5个重要步骤:①收集数据;②设计调査问卷;③用样本估计总体;④整理数据;⑤分析数据,这5个步骤正确排序为 (填序号).
解决上述问题要经历的几个重要步骤进行排序为②设计调查问卷,①收集数据,④整理数据,⑤分析数据,③用样本估计总体.
故答案为②①④⑤③
②①④⑤③
为了解七年级7800名男生1000米长跑的国家体质测试情况,从中随机抽查了150名男生的1000米长跑成绩进行统计分析,下列说法正确的是( )
A.每名男生是个体 B.7800名男生的1000米长跑成绩是总体
C.样本容量是150名 D.抽取的150名男生是样本
A.每名男生1000米长跑成绩是个体,故该选项不符合题意;
B.7800名男生的1000米长跑成绩是总体,故该选项符合题意;
C.样本容量是150,故该选项不符合题意;
D.抽取的150名男生的1000米长跑成绩是样本,故该选项不符合题意. 故选B.
B
下列调查活动中,适合全面调查的是( )
A.了解某批次汽车的抗撞能力
B.对重庆市学生“防疫知识”掌握度的调查
C.了解一沓钞票中有没有假钞
D.对某品牌牛奶合格率的调查
A项调查具有破坏性,适合抽样调查,故A错误;
B项调查范围广,适合抽样调查,故B错误;
C项是事关重大的调查,适合全面调查,故C正确;
D项调查范围广,适合抽样调查,故D错误.
故选C.
C
下面的抽样方法是简单随机抽样的是( )
A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2709的为三等奖
B.某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,称其质量是否合格
C.某学校从行政人员、教师、后勤人员中分别抽取2人、14人、4人了解对学校机构改革的意见
D.用抽签法从10件产品中抽取3件进行质量检验
D
简单随机抽样的特点是:每个样本单位被抽中的概率相等,样本的每个单位完全独立,彼此间无一定的关联性和排斥性,据此进行逐项分析,即可作答.
为了估计池塘里有多少条鱼,先捕100条做上标记,然后放回池塘里,过一段时间,待有标记的鱼完全混于鱼群后,再捕200条鱼,发现其中有标记的鱼有20条,那么池塘里大约有鱼( )
A.400条 B.600条 C.800条 D.1000条
D
气象站要测量一天中气温的变化情况,用 统计图比较合适;要反映100克牛奶中锌、镁、铁、钙等微量元素的含量,用 统计图比较合适;要想了解学校各年级人数多少的情况,用 统计图比较合适.
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系. 据此结合给出的情况选择合适的统计图即可.
折线
扇形
条形
(1)如果图中整个圆代表某厂3个工种的工人总数为2000人,那么扇形A代表的工种人数有 人.
(2)如果图中整个圆代表3种树共有1000棵,那么
扇形C代表的树有 棵.
(1)2000×25%=500(人),所以扇形A代表500人.
故答案为500.
500
250
(2)1000×(1-25%-50%)=250(棵).
故答案为250.
B
50%
A
25%
C
4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如下:
若该校共有 1200名学生,试估计全校每周课外阅读时间在5小时以上的学生人数为 人.
400
所以,估计全校每周课外阅读时间在5小时以上的学生人数为400人,故答案为 400.
将40个数据分成6组,其中第1~4组数据的频数分别是10、5、7、6,第5组数据占10%,则第6组数据占( )
A.25% B.30% C.15% D.20%
有40个数据,第5组数据占10%,
则第5组的频数为40×10%=4,
第6组的频数为40-10-5-7-6-4=8,
第6组的占比为8÷40=20%.
故选D.
D
为了解某校七年级学生参加消防知识竞赛的成绩(均为整数),从中抽取了1%的学生的竞赛成绩,整理后绘制了如图所示的频数直方图(各组只含最小值,不含最大值),若竞赛成绩在90分及以上的学生可以获得奖励,则估计该校获得奖励的七年级学生有 人.
2000
参加竞赛的总人数为:4+7+10+13+16-50(人),则七年级学生总人数为:50÷1%=5000(人),所以,该校获得奖励的七年级学生有:
故答案为2000.
在一次体育水平测试中,甲、乙两校均有100名学生参加,其中:甲校男生成绩的优秀率为70%,女生成绩的优秀率为50%;乙校男生成绩的优秀率为60%,女生成绩的优秀率为40%,对于此次测试,给出下列三个结论:
①甲校学生成绩的优秀率大于乙校学生成绩的优秀率;
②甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率;
③甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定. 其中所有正确结论的序号是 .
②③
由题意得,甲校学生成绩优秀率在50%与70%之间,乙校学生成绩的优秀率在40%与60%之间,不能确定哪个学校的优秀率大,①错误;
正确的结论序号是②③.
故答案为②③.
为了解社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民层开展了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图,若该社区中20~60岁的居民约8000人,请根据图中信息估算其中20~40岁的人群中最喜欢微信支付方式的人数为 人.
1600
本次调查总人数为
(120+80)÷40%=500(人)
所以估算其中20~40岁的人群
中最喜欢微信支付方式的人数约为:
为了解居民的健步走情况,小文调査了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图,根据图表提供的信息,回答下列问题:
(1)小文此次调查的样本容量是 ;
(2)行走步数为4~8千步的人数为 人;
(3)行走步数为12~16千步的扇形圆心角
为 °;
(4)如该小区有3000名居民,请估算一下该小区行走步数为0 ~4千步的人数.
为了解居民的健步走情况,小文调査了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图,根据图表提供的信息,回答下列问题:
(1)小文此次调查的样本容量是 ;
(2)行走步数为4~8千步的人数为 人;
(1)小文此次调查的样本容量为
70÷35%=200. 故答案为200.
(2)行走步数为4~8千步的人数为:200×25%=50(人).
故答案为50.
200
50
(3)行走步数为12~16千步的扇形圆心角为360°×20%=72°.
故答案为72.
(3)行走步数为12~16千步的扇形圆心角为 °;
(4)如该小区有3000名居民,请估算一下该小区行走步数为0 ~4千步的人数.
72
章综合复习
【第十二章 数据的收集、整理与描述】
数据的收集
、整理与描述
全面调查
数据的收集
抽样调查
折线统计图
数据的整理与描述
条形统计图
趋势图
扇形统计图
直方图
频数分布表
频数分布直方图
总体、个体、样本、样本容量
用样本估计总体
简单随机抽样
根据统计图表的不同特点,选择合适的描述方法.
全面调查:考察全体对象的调查叫作全面调查.
概念
注:总体是由个体组成的,个体是总体中的一个.
要点
全面调查
总体与个体:要考察的全体对象称为总体,组成总体的每一个调查对象称为个体.
适用范围:一般地,当调查的范围小、调查不具有破坏性、数据要求准确全面时,采用全面调查.
优点:结果准确,有利于全面了解数据;
缺点:花费时间长,消耗的人力、物力大,易受条件限制,不适用于具有破坏性的调查.
概念
抽样调查
抽样调查:只抽取一部分对象进行调查,然后根据调查数据推断全体对象的情况,这种方法称为抽样调查.
适用范围:一般地,当调查具有破坏性、调查范围大、受条件限制无法进行全面调查或全面调查的意义、价值不大时,采用抽样调查.
优点:调查范围小,省时省力;
缺点:结果的准确程度受抽取样本的影响,不能全面了解数据.
要点
方法:简单随机抽样.
从总体中被抽取调查的那些个体构成总体的一个样本,样本中包含的个体的数目称为样本容量.
概念
要点
样本
(1)总体包含所有个体,样本只包括所抽取的个体;
(2)样本是总体的一部分,一个总体可以有多个样本;
(3)样本容量是样本中所含个体的个数,不是调查对象,而且没有单位.
概念
用样本估计总体
简单随机抽样
简单随机抽样:在抽取样本的过程中,总体中的每一个个体都有相等的机会被抽到,像这样的抽样方法称为简单随机抽样.
(1)一般情况下,样本容量越大,样本对总体的估计越准确,在解决实际问题中,要根据具体情况确定样本容量的大小;
(2)抽取的样本在一定程度上能够反映总体,为了使样本能较好地反映总体情况,在选取样本时,除了样本容量要合适,抽取的样本也要具有一定的代表性.
注:当总体中的个体数较多时,常采用简单随机抽样来进行调查.
表示
要点
扇形图
扇形图用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
(1)特点:扇形图可以直观地反映各部分占整体的百分比,但不能清楚地表明每一个项目的具体数目;
(2)扇形图中,各部分占整体的百分比之和为100%或1.
(3)在扇形图中,用圆代表整体,但圆的大小与具体的数量的多少无关.
扇形图中圆心角的度数:在扇形图中,每部分所对应的扇形圆心角的度数=该部分占总体的百分比×360°.即扇形面积占圆面积的百分比.
方法
统计图的选择
(1)需要表达的数据是分散的,并且需要清晰地表示出各组实际数据,选择条形图较为适宜;
(2)需要表达各组数据占整体的百分比,选择扇形图较为适宜;
(3)需要清晰地显示各组数据在一段时期内的变化,或分析数据的变化趋势,选择折线图较为适宜.
注意
在同一统计图中,为了表示两组或两组以上的数据,用于不同数据之间的比较,可绘制复合折线图和复合条形图.
概念
直方图
注意
是一个数值,没有单位.
把数据分为若干组:
组距:每一组两个端点之间的距离叫组距;
组数:把数分成若干组,分成组的个数叫组数;频数:落在各小组内的数据的个数叫该组的频数;
频率:频数占总数的百分比叫频率,频率=
当数据在100个以内时,根据数据的多少通常分成5-12组.
一般地,组数= (向下取整)+1
表示方法
直方图
意义
频数分布直方图是一种特殊的条形图,它将统计对象的数据进行了分组,画在横轴上,对于等距分组的频数分布直方图,通常纵轴表示各组数据的频数.(高表示相应各组数据的频数,即各小长方形的高之比等于所对应的各组数据的频数之比 )
直方图是条形图,但条形图不是直方图
频数分布直方图由横轴、纵轴、小长方形三部分构成;横轴表示分组情况,纵轴表示频数与组距的比值.
画法
直方图
绘制频数分布直方图的步骤:
(1)计算最大值与最小值的差;
(2)决定组距和组数;
(3)列频数分布表;
(4)画频数分布直方图.
概念
趋势图
趋势图:用一条线(直线或曲线)来描述一个量与另一个量之间关系的统计图,叫作趋势图.
特点
趋势图比较清楚地表示了两个量之间的关系,有利于根据一个量的变化,预测另一个量的变化趋势.
通过“数据的分析”的学习,我们知道了统计调査活动要经历的5个重要步骤:①收集数据;②设计调査问卷;③用样本估计总体;④整理数据;⑤分析数据,这5个步骤正确排序为 (填序号).
解决上述问题要经历的几个重要步骤进行排序为②设计调查问卷,①收集数据,④整理数据,⑤分析数据,③用样本估计总体.
故答案为②①④⑤③
②①④⑤③
为了解七年级7800名男生1000米长跑的国家体质测试情况,从中随机抽查了150名男生的1000米长跑成绩进行统计分析,下列说法正确的是( )
A.每名男生是个体 B.7800名男生的1000米长跑成绩是总体
C.样本容量是150名 D.抽取的150名男生是样本
A.每名男生1000米长跑成绩是个体,故该选项不符合题意;
B.7800名男生的1000米长跑成绩是总体,故该选项符合题意;
C.样本容量是150,故该选项不符合题意;
D.抽取的150名男生的1000米长跑成绩是样本,故该选项不符合题意. 故选B.
B
下列调查活动中,适合全面调查的是( )
A.了解某批次汽车的抗撞能力
B.对重庆市学生“防疫知识”掌握度的调查
C.了解一沓钞票中有没有假钞
D.对某品牌牛奶合格率的调查
A项调查具有破坏性,适合抽样调查,故A错误;
B项调查范围广,适合抽样调查,故B错误;
C项是事关重大的调查,适合全面调查,故C正确;
D项调查范围广,适合抽样调查,故D错误.
故选C.
C
下面的抽样方法是简单随机抽样的是( )
A.在某年明信片销售活动中,规定每100万张为一个开奖组,通过随机抽取的方式确定号码的后四位为2709的为三等奖
B.某车间包装一种产品,在自动包装的传送带上,每隔30分钟抽一包产品,称其质量是否合格
C.某学校从行政人员、教师、后勤人员中分别抽取2人、14人、4人了解对学校机构改革的意见
D.用抽签法从10件产品中抽取3件进行质量检验
D
简单随机抽样的特点是:每个样本单位被抽中的概率相等,样本的每个单位完全独立,彼此间无一定的关联性和排斥性,据此进行逐项分析,即可作答.
为了估计池塘里有多少条鱼,先捕100条做上标记,然后放回池塘里,过一段时间,待有标记的鱼完全混于鱼群后,再捕200条鱼,发现其中有标记的鱼有20条,那么池塘里大约有鱼( )
A.400条 B.600条 C.800条 D.1000条
D
气象站要测量一天中气温的变化情况,用 统计图比较合适;要反映100克牛奶中锌、镁、铁、钙等微量元素的含量,用 统计图比较合适;要想了解学校各年级人数多少的情况,用 统计图比较合适.
条形统计图能很容易看出数量的多少;折线统计图不仅容易看出数量的多少,而且能反映数量的增减变化情况;扇形统计图能反映部分与整体的关系. 据此结合给出的情况选择合适的统计图即可.
折线
扇形
条形
(1)如果图中整个圆代表某厂3个工种的工人总数为2000人,那么扇形A代表的工种人数有 人.
(2)如果图中整个圆代表3种树共有1000棵,那么
扇形C代表的树有 棵.
(1)2000×25%=500(人),所以扇形A代表500人.
故答案为500.
500
250
(2)1000×(1-25%-50%)=250(棵).
故答案为250.
B
50%
A
25%
C
4月23日是世界读书日,这天某校为了解学生课外阅读情况,随机收集了30名学生每周课外阅读的时间,统计如下:
若该校共有 1200名学生,试估计全校每周课外阅读时间在5小时以上的学生人数为 人.
400
所以,估计全校每周课外阅读时间在5小时以上的学生人数为400人,故答案为 400.
将40个数据分成6组,其中第1~4组数据的频数分别是10、5、7、6,第5组数据占10%,则第6组数据占( )
A.25% B.30% C.15% D.20%
有40个数据,第5组数据占10%,
则第5组的频数为40×10%=4,
第6组的频数为40-10-5-7-6-4=8,
第6组的占比为8÷40=20%.
故选D.
D
为了解某校七年级学生参加消防知识竞赛的成绩(均为整数),从中抽取了1%的学生的竞赛成绩,整理后绘制了如图所示的频数直方图(各组只含最小值,不含最大值),若竞赛成绩在90分及以上的学生可以获得奖励,则估计该校获得奖励的七年级学生有 人.
2000
参加竞赛的总人数为:4+7+10+13+16-50(人),则七年级学生总人数为:50÷1%=5000(人),所以,该校获得奖励的七年级学生有:
故答案为2000.
在一次体育水平测试中,甲、乙两校均有100名学生参加,其中:甲校男生成绩的优秀率为70%,女生成绩的优秀率为50%;乙校男生成绩的优秀率为60%,女生成绩的优秀率为40%,对于此次测试,给出下列三个结论:
①甲校学生成绩的优秀率大于乙校学生成绩的优秀率;
②甲、乙两校所有男生成绩的优秀率大于甲、乙两校所有女生成绩的优秀率;
③甲校学生成绩的优秀率与甲、乙两校所有学生成绩的优秀率的大小关系不确定. 其中所有正确结论的序号是 .
②③
由题意得,甲校学生成绩优秀率在50%与70%之间,乙校学生成绩的优秀率在40%与60%之间,不能确定哪个学校的优秀率大,①错误;
正确的结论序号是②③.
故答案为②③.
为了解社区20~60岁居民最喜欢的支付方式,某兴趣小组对社区内该年龄段的部分居民层开展了随机问卷调查(每人只能选择其中一项),并将调查数据整理后绘成如下两幅不完整的统计图,若该社区中20~60岁的居民约8000人,请根据图中信息估算其中20~40岁的人群中最喜欢微信支付方式的人数为 人.
1600
本次调查总人数为
(120+80)÷40%=500(人)
所以估算其中20~40岁的人群
中最喜欢微信支付方式的人数约为:
为了解居民的健步走情况,小文调査了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图,根据图表提供的信息,回答下列问题:
(1)小文此次调查的样本容量是 ;
(2)行走步数为4~8千步的人数为 人;
(3)行走步数为12~16千步的扇形圆心角
为 °;
(4)如该小区有3000名居民,请估算一下该小区行走步数为0 ~4千步的人数.
为了解居民的健步走情况,小文调査了部分居民某天行走的步数(单位:千步),并将样本数据整理绘制成如下不完整的频数分布直方图和扇形统计图,根据图表提供的信息,回答下列问题:
(1)小文此次调查的样本容量是 ;
(2)行走步数为4~8千步的人数为 人;
(1)小文此次调查的样本容量为
70÷35%=200. 故答案为200.
(2)行走步数为4~8千步的人数为:200×25%=50(人).
故答案为50.
200
50
(3)行走步数为12~16千步的扇形圆心角为360°×20%=72°.
故答案为72.
(3)行走步数为12~16千步的扇形圆心角为 °;
(4)如该小区有3000名居民,请估算一下该小区行走步数为0 ~4千步的人数.
72
同课章节目录
