10.3实际问题与二元一次方程组 第3课时 课件(共22张PPT) 人教版(2024)数学七年级下册
文档属性
| 名称 | 10.3实际问题与二元一次方程组 第3课时 课件(共22张PPT) 人教版(2024)数学七年级下册 |  | |
| 格式 | pptx | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:55:32 | ||
图片预览




文档简介
(共22张PPT)
实际问题与二元一次方程组(第3课时)
数学人教版(2024)七年级下册
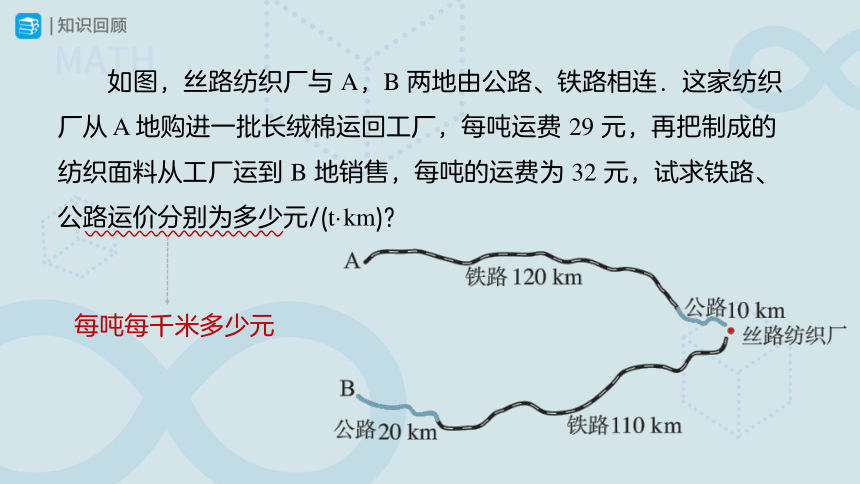
如图,丝路纺织厂与 A,B 两地由公路、铁路相连.这家纺织厂从 A 地购进一批长绒棉运回工厂,每吨运费 29 元,再把制成的纺织面料从工厂运到 B 地销售,每吨的运费为 32 元,试求铁路、公路运价分别为多少元/(t·km)?
每吨每千米多少元
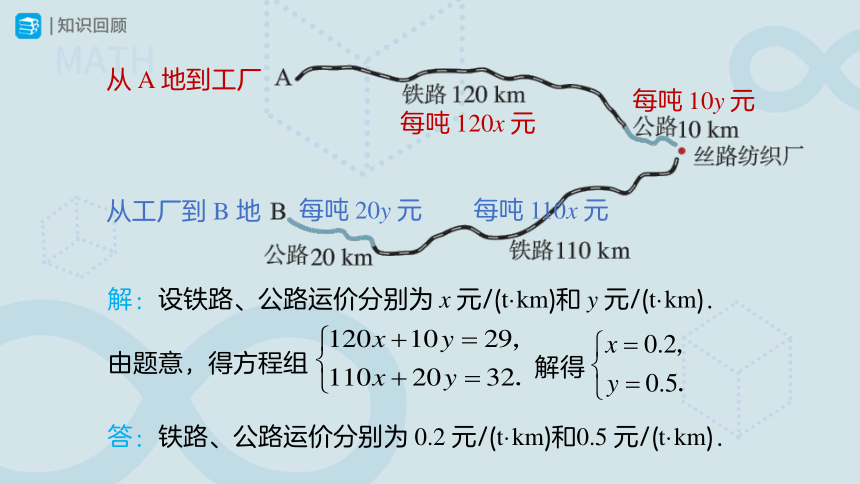
解:设铁路、公路运价分别为 x 元/(t·km)和 y 元/(t·km).
每吨 120x 元
每吨 10y 元
每吨 20y 元
每吨 110x 元
从 A 地到工厂
从工厂到 B 地
由题意,得方程组
答:铁路、公路运价分别为 0.2 元/(t·km)和0.5 元/(t·km).
解得
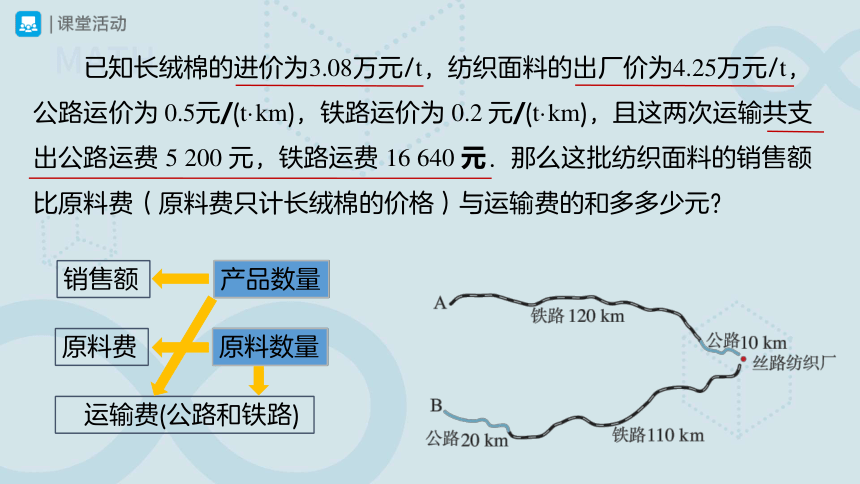
如图,丝路纺织厂与 A,B 两地由公路、铁路相连.这家纺织厂从 A 地购进一批长绒棉运回工厂,制成纺织面料运往 B地.已知长绒棉的进价为3.08万元/t,纺织面料的出厂价为4.25万元/t,公路运价为 0.5 元/(t·km),铁路运价为 0.2 元/(t·km),且这两次运输共支出公路运费 5 200 元,铁路运费 16 640 元.那么这批纺织面料的销售额比原料费(原料费只计长绒棉的价格)与运输费的和多多少元?
思考:要求“这批纺织面料的销售额比原料费与运输费的和多多少元?”我们必须知道什么?
已知长绒棉的进价为3.08万元/t,纺织面料的出厂价为4.25万元/t,公路运价为 0.5元/(t·km),铁路运价为 0.2 元/(t·km),且这两次运输共支出公路运费 5 200 元,铁路运费 16 640 元.那么这批纺织面料的销售额比原料费(原料费只计长绒棉的价格)与运输费的和多多少元?
销售额
原料费
运输费(公路和铁路)
原料数量
产品数量
原料数量
产品数量
分析:销售额与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们设购买 x t 长绒棉,制成 y t 纺织面料.
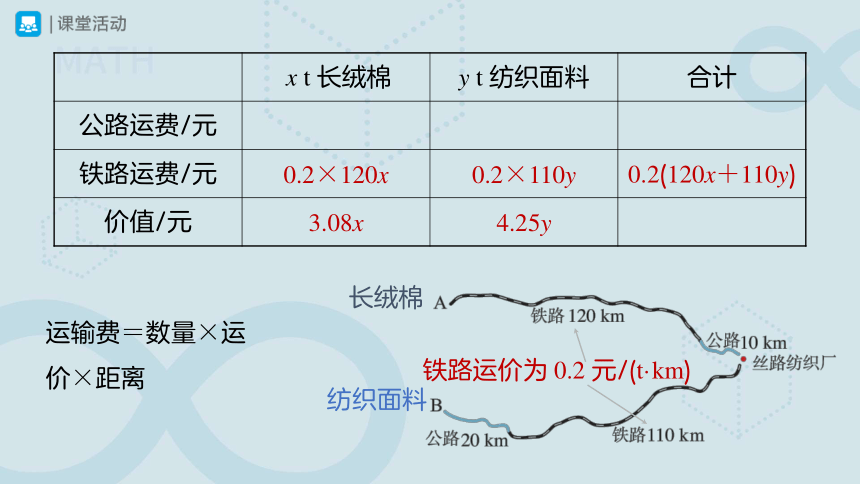
思考:你能根据题中数量关系完成下表吗?
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元
总价=单价×数量
单价:3.08元/t
单价:4.25元/t
长绒棉
纺织面料
3.08x
4.25y
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元 3.08x 4.25y
铁路运价为 0.2 元/(t·km)
0.2×120x
0.2×110y
0.2(120x+110y)
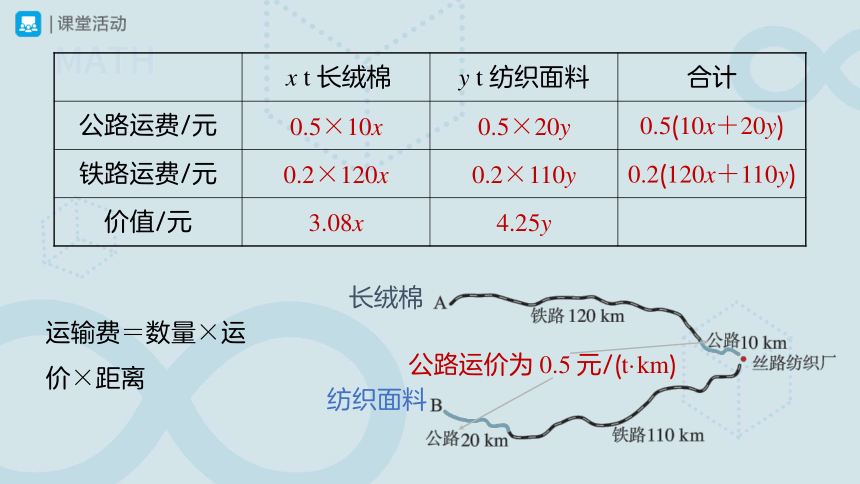
运输费=数量×运价×距离
长绒棉
纺织面料
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元 0.2×120x 0.2×110y 0.2(120x+110y)
价值/元 3.08x 4.25y
公路运价为 0.5 元/(t·km)
0.5×10x
0.5×20y
0.5(10x+20y)
运输费=数量×运价×距离
长绒棉
纺织面料
x t 长绒棉 y t 纺织面料 合计
公路运费/元 0.5×10x 0.5×20y 0.5(10x+20y)
铁路运费/元 0.2×120x 0.2×110y 0.2(120x+110y)
价值/元 3.08x 4.25y
思考:你发现相等关系了吗?如何列方程组并求解?
根据两次运输共支出公路运费 5 200 元,铁路运费 16 640 元,列方程组
解:设购买 x t 长绒棉,制成 y t 纺织面料.
所以丝路纺织厂从 A 地购买了 400 t 长绒棉,制成 320 t 纺织面料运往 B 地.
化简,得
解得
由题意,得方程组
思考:这批纺织面料的销售额比原料费与运输费的和多多少元?
销售额:4.25y=4.25×320=1 360(万元);
原料费:3.08x=3.08×400=1 232(万元);
运输费:5 200+16 640=21 840(元);
13 600 000-(12 320 000+21 840)=1 258 160(元).
这批纺织面料的销售额比原料费与运输费的和多 1 258 160 元.
归纳
若在直接设要求的量为未知数不容易列方程(组)时,应设间接未知数,求得未知数的值后再计算要求的量.
从以上探究可以看出,方程组是解决含有多个未知数问题的重要工具.用方程组解决问题时,要根据问题中的数量关系列出方程组,求出方程组的解后,应进一步考虑它是否符合问题的实际意义.
问题
一个农机服务队有技术员工和辅助员工共 15 人,技术员工人数是辅助员工人数的 2 倍.服务队计划对员工发放奖金共计 20 000 元.按每名技术员工 A 元和每名辅助员工 B 元两种标准发放,其中 A,B 均不小于 800,且 A 不小于 B,并且 A,B 都是 100 的整数倍.(注:农机服务队是一种农业机械化服务组织,为农民提供耕种、收割等有偿服务.)
(1)求该农机服务队中技术员工和辅助员工的人数;
(2)求本次奖金发放的具体方案.
分析:(1)①由“服务队有技术员工和辅助员工共 15 人”得相等关系:______________________.由“技术员工人数是辅助员工人数的 2 倍”得相等关系:
_________________.
②设该农机服务队有技术员工 x 人,辅助员工 y 人,根据①中的两个相等关系可列方程组 解得 即该农机服务队有技术员工___人,辅助员工___人.
技术员工人数+辅助员工人数=15
技术员工人数=辅助员工人数×2
x+y=15
x=2y
10
5
10
5
分析:(2)①由“服务队计划对员工发放奖金共计 20 000 元”得相等关系:______________________.
据此可列出关于 A,B 的二元一次方程:__________.
②因为 A≥B≥800,且 A,B 都是 100 的整数倍,
所以当 B=800 时,A=_____;
当 B=900 时,A=_____( A 不是 100 的整数倍,舍去);
当 B=1 000 时,A=_____;
当 B=1 100 时,A=____( A 不是 100 的整数倍,舍去);
技术员工总奖金+辅助员工总奖金=20 000 元
10A+5B=20 000
1 600
1 550
1 500
1 450
当 B=1 200 时,A=_____;
当 B=1 300 时,A=____( A 不是 100 的整数倍,舍去);
当 B=1 400 时,A=_____( A<B,舍去);
由此再取下去都不符合题意.
所以本次奖金发放的具体方案有 3 种:
方案 1:技术员工每人_____元,辅助员工每人 800 元;
方案 2:技术员工每人_____元,辅助员工每人 1 000 元;
方案 3:技术员工每人_____元,辅助员工每人 1 200 元.
1 400
1 350
1 300
1 600
1 500
1 400
归纳
要求两个量,且已知两个相等关系,一般列二元一次方程组即可求解;若要求两个量,且只知一个相等关系,则一般列二元一次方程,然后根据问题的实际情况讨论得出符合题意的结果.
例 某工厂去年的总产值比总支出多 500 万元.由于今年总产值比去年增加 15%,总支出比去年节约 10%,因此,今年总产值比总支出多 950 万元.今年的总产值和总支出各是多少万元?
分析:解决此类问题要先明确几个基本关系:
(1)增长量=原有量×增长率;
(2)原有量=现有量-增长量;
(3)现有量=原有量×(1+增长率).
再根据相等关系列方程组.
解:设去年总产值是 x 万元,总支出是 y 万元,列表如下:
所以(1+15%)x=2 300,(1-10%)y=1 350.
解得
总产值/万元 总支出/万元 差/万元
去年 x y 500
今年 (1+15%)x (1-10%)y 950
答:今年的总产值是 2 300 万元,总支出是 1 350 万元.
由题意,得方程组
归纳
画表格巧解增长率问题
在此类数量关系比较复杂的增长率题目中,仅靠想象寻找相等关系或列方程组,难免会出现顾此失彼的情况,如果能借助表格分析,将会更容易理清解题思路,从而列出方程组.
列二元一次方程组解决复杂的实际问题
方案设计类问题
设间接未知数解决问题
实际问题与二元一次方程组(第3课时)
数学人教版(2024)七年级下册
如图,丝路纺织厂与 A,B 两地由公路、铁路相连.这家纺织厂从 A 地购进一批长绒棉运回工厂,每吨运费 29 元,再把制成的纺织面料从工厂运到 B 地销售,每吨的运费为 32 元,试求铁路、公路运价分别为多少元/(t·km)?
每吨每千米多少元
解:设铁路、公路运价分别为 x 元/(t·km)和 y 元/(t·km).
每吨 120x 元
每吨 10y 元
每吨 20y 元
每吨 110x 元
从 A 地到工厂
从工厂到 B 地
由题意,得方程组
答:铁路、公路运价分别为 0.2 元/(t·km)和0.5 元/(t·km).
解得
如图,丝路纺织厂与 A,B 两地由公路、铁路相连.这家纺织厂从 A 地购进一批长绒棉运回工厂,制成纺织面料运往 B地.已知长绒棉的进价为3.08万元/t,纺织面料的出厂价为4.25万元/t,公路运价为 0.5 元/(t·km),铁路运价为 0.2 元/(t·km),且这两次运输共支出公路运费 5 200 元,铁路运费 16 640 元.那么这批纺织面料的销售额比原料费(原料费只计长绒棉的价格)与运输费的和多多少元?
思考:要求“这批纺织面料的销售额比原料费与运输费的和多多少元?”我们必须知道什么?
已知长绒棉的进价为3.08万元/t,纺织面料的出厂价为4.25万元/t,公路运价为 0.5元/(t·km),铁路运价为 0.2 元/(t·km),且这两次运输共支出公路运费 5 200 元,铁路运费 16 640 元.那么这批纺织面料的销售额比原料费(原料费只计长绒棉的价格)与运输费的和多多少元?
销售额
原料费
运输费(公路和铁路)
原料数量
产品数量
原料数量
产品数量
分析:销售额与产品数量有关,原料费与原料数量有关,而公路运费和铁路运费与产品数量和原料数量都有关.因此,我们设购买 x t 长绒棉,制成 y t 纺织面料.
思考:你能根据题中数量关系完成下表吗?
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元
总价=单价×数量
单价:3.08元/t
单价:4.25元/t
长绒棉
纺织面料
3.08x
4.25y
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元
价值/元 3.08x 4.25y
铁路运价为 0.2 元/(t·km)
0.2×120x
0.2×110y
0.2(120x+110y)
运输费=数量×运价×距离
长绒棉
纺织面料
x t 长绒棉 y t 纺织面料 合计
公路运费/元
铁路运费/元 0.2×120x 0.2×110y 0.2(120x+110y)
价值/元 3.08x 4.25y
公路运价为 0.5 元/(t·km)
0.5×10x
0.5×20y
0.5(10x+20y)
运输费=数量×运价×距离
长绒棉
纺织面料
x t 长绒棉 y t 纺织面料 合计
公路运费/元 0.5×10x 0.5×20y 0.5(10x+20y)
铁路运费/元 0.2×120x 0.2×110y 0.2(120x+110y)
价值/元 3.08x 4.25y
思考:你发现相等关系了吗?如何列方程组并求解?
根据两次运输共支出公路运费 5 200 元,铁路运费 16 640 元,列方程组
解:设购买 x t 长绒棉,制成 y t 纺织面料.
所以丝路纺织厂从 A 地购买了 400 t 长绒棉,制成 320 t 纺织面料运往 B 地.
化简,得
解得
由题意,得方程组
思考:这批纺织面料的销售额比原料费与运输费的和多多少元?
销售额:4.25y=4.25×320=1 360(万元);
原料费:3.08x=3.08×400=1 232(万元);
运输费:5 200+16 640=21 840(元);
13 600 000-(12 320 000+21 840)=1 258 160(元).
这批纺织面料的销售额比原料费与运输费的和多 1 258 160 元.
归纳
若在直接设要求的量为未知数不容易列方程(组)时,应设间接未知数,求得未知数的值后再计算要求的量.
从以上探究可以看出,方程组是解决含有多个未知数问题的重要工具.用方程组解决问题时,要根据问题中的数量关系列出方程组,求出方程组的解后,应进一步考虑它是否符合问题的实际意义.
问题
一个农机服务队有技术员工和辅助员工共 15 人,技术员工人数是辅助员工人数的 2 倍.服务队计划对员工发放奖金共计 20 000 元.按每名技术员工 A 元和每名辅助员工 B 元两种标准发放,其中 A,B 均不小于 800,且 A 不小于 B,并且 A,B 都是 100 的整数倍.(注:农机服务队是一种农业机械化服务组织,为农民提供耕种、收割等有偿服务.)
(1)求该农机服务队中技术员工和辅助员工的人数;
(2)求本次奖金发放的具体方案.
分析:(1)①由“服务队有技术员工和辅助员工共 15 人”得相等关系:______________________.由“技术员工人数是辅助员工人数的 2 倍”得相等关系:
_________________.
②设该农机服务队有技术员工 x 人,辅助员工 y 人,根据①中的两个相等关系可列方程组 解得 即该农机服务队有技术员工___人,辅助员工___人.
技术员工人数+辅助员工人数=15
技术员工人数=辅助员工人数×2
x+y=15
x=2y
10
5
10
5
分析:(2)①由“服务队计划对员工发放奖金共计 20 000 元”得相等关系:______________________.
据此可列出关于 A,B 的二元一次方程:__________.
②因为 A≥B≥800,且 A,B 都是 100 的整数倍,
所以当 B=800 时,A=_____;
当 B=900 时,A=_____( A 不是 100 的整数倍,舍去);
当 B=1 000 时,A=_____;
当 B=1 100 时,A=____( A 不是 100 的整数倍,舍去);
技术员工总奖金+辅助员工总奖金=20 000 元
10A+5B=20 000
1 600
1 550
1 500
1 450
当 B=1 200 时,A=_____;
当 B=1 300 时,A=____( A 不是 100 的整数倍,舍去);
当 B=1 400 时,A=_____( A<B,舍去);
由此再取下去都不符合题意.
所以本次奖金发放的具体方案有 3 种:
方案 1:技术员工每人_____元,辅助员工每人 800 元;
方案 2:技术员工每人_____元,辅助员工每人 1 000 元;
方案 3:技术员工每人_____元,辅助员工每人 1 200 元.
1 400
1 350
1 300
1 600
1 500
1 400
归纳
要求两个量,且已知两个相等关系,一般列二元一次方程组即可求解;若要求两个量,且只知一个相等关系,则一般列二元一次方程,然后根据问题的实际情况讨论得出符合题意的结果.
例 某工厂去年的总产值比总支出多 500 万元.由于今年总产值比去年增加 15%,总支出比去年节约 10%,因此,今年总产值比总支出多 950 万元.今年的总产值和总支出各是多少万元?
分析:解决此类问题要先明确几个基本关系:
(1)增长量=原有量×增长率;
(2)原有量=现有量-增长量;
(3)现有量=原有量×(1+增长率).
再根据相等关系列方程组.
解:设去年总产值是 x 万元,总支出是 y 万元,列表如下:
所以(1+15%)x=2 300,(1-10%)y=1 350.
解得
总产值/万元 总支出/万元 差/万元
去年 x y 500
今年 (1+15%)x (1-10%)y 950
答:今年的总产值是 2 300 万元,总支出是 1 350 万元.
由题意,得方程组
归纳
画表格巧解增长率问题
在此类数量关系比较复杂的增长率题目中,仅靠想象寻找相等关系或列方程组,难免会出现顾此失彼的情况,如果能借助表格分析,将会更容易理清解题思路,从而列出方程组.
列二元一次方程组解决复杂的实际问题
方案设计类问题
设间接未知数解决问题
同课章节目录
