浙江省杭州市2024—2025学年度八年级下学期期末训练卷(含解析)
文档属性
| 名称 | 浙江省杭州市2024—2025学年度八年级下学期期末训练卷(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 2.6MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 浙教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 15:09:43 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
浙江省杭州市2024—2025学年度八年级下学期期末训练卷
一.选择题(共16小题)
1.使得式子有意义的x的取值范围是( )
A.x≥4 B.x>4 C.x≤4 D.x<4
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.若2<a<3,则( )
A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5
4.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A.中位数是8 B.众数是9 C.平均数是8 D.方差是0
5.如图,在菱形ABCD中,E是对角线AC的中点,EF∥CB,交AB于点F,如果EF=3.5,那么菱形ABCD的周长为( )
A.28 B.14 C.7 D.3.5
6.反比例函数的图象上有A(a,y1),B(2a,y2),C(3a,y3)三点( )
A.若y1<0,则y1﹣y2>y2﹣y3
B.若y1>0,则y1﹣y2>y2﹣y3
C.若y1>0,则|y1﹣y2|<|y2﹣y3|
D.若y1<0,则|y1﹣y2|<|y2﹣y3|
7.若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
8.如图所示,E是菱形ABCD对角线AC上的一点,若BC=6,DE=4,设AE=x,CE=y,则下列代数式为定值的是( )
A.y+x B.xy C.y﹣x D.y2+x2
9.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
10.在数学活动课上,老师和同学们判断一个四边形模具是否为菱形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否互相平分且相等
B.测量对角线是否互相平分且垂直
C.测量三条边是否相等
D.测量对角线是否互相垂直且一组邻边相等
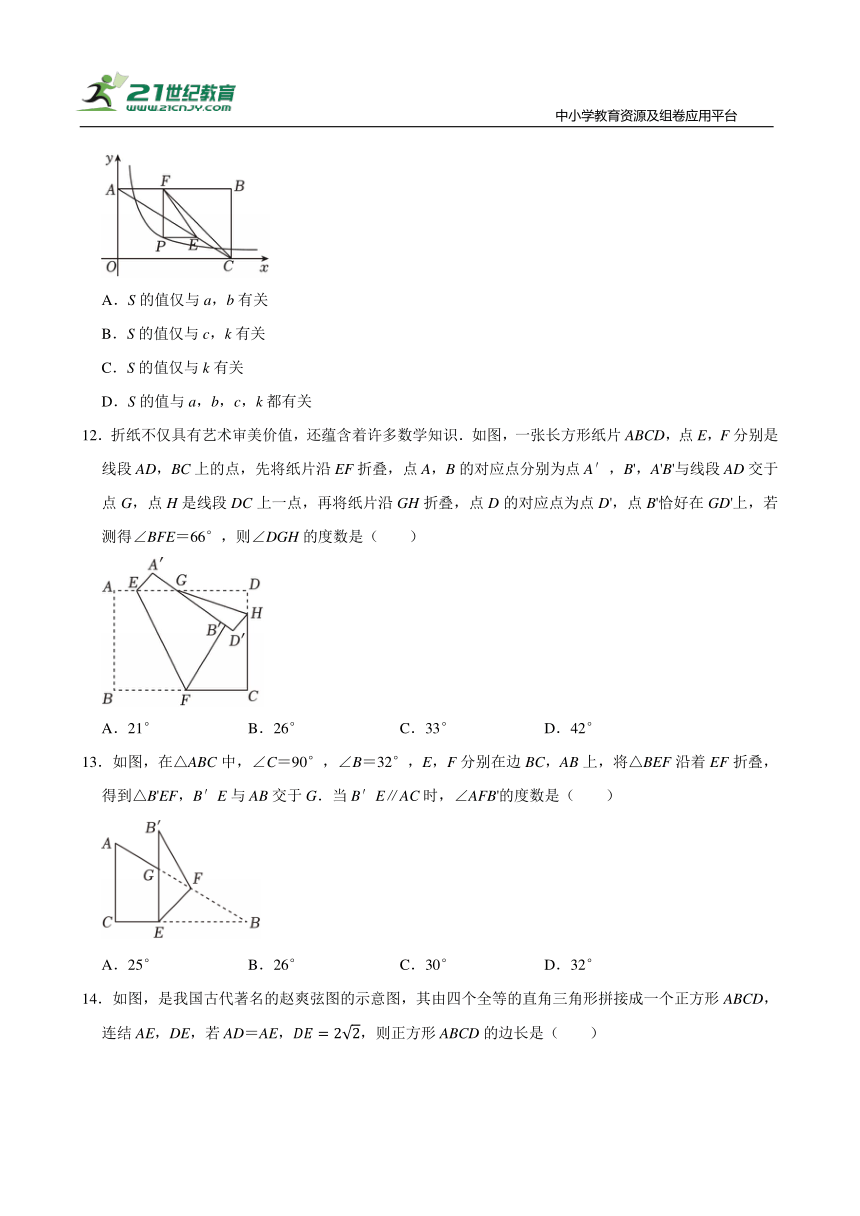
11.如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关
B.S的值仅与c,k有关
C.S的值仅与k有关
D.S的值与a,b,c,k都有关
12.折纸不仅具有艺术审美价值,还蕴含着许多数学知识.如图,一张长方形纸片ABCD,点E,F分别是线段AD,BC上的点,先将纸片沿EF折叠,点A,B的对应点分别为点A′,B',A'B'与线段AD交于点G,点H是线段DC上一点,再将纸片沿GH折叠,点D的对应点为点D',点B'恰好在GD'上,若测得∠BFE=66°,则∠DGH的度数是( )
A.21° B.26° C.33° D.42°
13.如图,在△ABC中,∠C=90°,∠B=32°,E,F分别在边BC,AB上,将△BEF沿着EF折叠,得到△B'EF,B′E与AB交于G.当B′E∥AC时,∠AFB'的度数是( )
A.25° B.26° C.30° D.32°
14.如图,是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,连结AE,DE,若AD=AE,,则正方形ABCD的边长是( )
A. B. C. D.
15.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,射线EG与BC的延长线相交于点P.若∠P=30°,则的值是( )
A. B.3 C. D.
16.“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
二.填空题(共8小题)
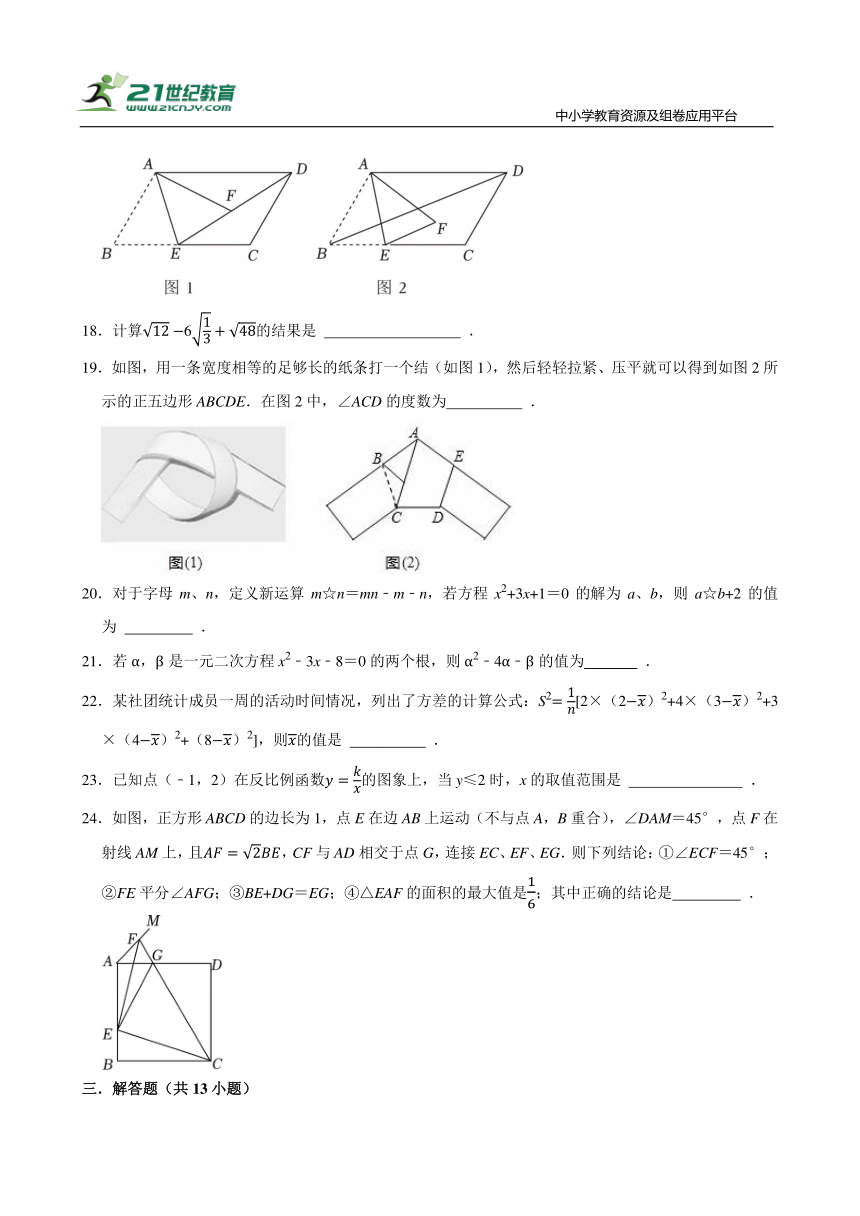
17.如图,在 ABCD中,∠ABC=60°,AB=6,BC=10,点E是边BC上一点,将△ABE沿AE折叠后,点B的对应点为点F.
(1)如图1,连接DE,若点F恰好落在边DE上.则BE的长为 .
(2)如图2,连接BD,若EF∥BD,则BE的长为 .
18.计算6的结果是 .
19.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 .
20.对于字母m、n,定义新运算m☆n=mn﹣m﹣n,若方程x2+3x+1=0的解为a、b,则a☆b+2的值为 .
21.若α,β是一元二次方程x2﹣3x﹣8=0的两个根,则α2﹣4α﹣β的值为 .
22.某社团统计成员一周的活动时间情况,列出了方差的计算公式:S2[2×(2)2+4×(3)2+3×(4)2+(8)2],则的值是 .
23.已知点(﹣1,2)在反比例函数的图象上,当y≤2时,x的取值范围是 .
24.如图,正方形ABCD的边长为1,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②FE平分∠AFG;③BE+DG=EG;④△EAF的面积的最大值是;其中正确的结论是 .
三.解答题(共13小题)
25.我们常常把一张A4纸通过折叠的方式得到它的对角线,如图1.折纸活动中,通过点与点重合或边与边重合,才能得到精准的折叠.现有一张A4纸张(矩形ABCD),如图2,设折叠后B'C边与AD边重叠的点为E.
(1)请用尺规作图的方式在图2中画出点E.
(2)根据以上折纸活动的提示,描述折出A4纸(矩形ABCD)对角线的两个步骤.
26.在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
27.定义:有一组邻边垂直且对角线相等的四边形为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 .
(2)如图1,在3×3方格纸中,A,B,C在格点上,请画出两个符合条件的不全等的垂等四边形,使AC,BD是对角线,点D在格点上.
(3)如图2,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,AE=AF=CG且∠DGC=∠DEG,求证:四边形DEFG是垂等四边形.
28.计算题:
(1);
(2).
29.已知关于x的一元二次方程x2﹣(2m+1)x+m﹣2=0.
(1)求证:不论m取何值,方程总有两个不相等的实数根;
(2)若方程有两个实数根为x1,x2,且x1+x2+3x1x2=1,求m的值.
30.2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,该意见对学生睡眠时间提出了新的要求.为了了解某校初二年级学生的睡眠时长,随机抽取了初二年级男生和女生各20位,对其同一天的睡眠时长进行调查,并对数据进行收集、整理、描述和分析.下面给出了相关信息.
a.睡眠时长(单位:小时):
男生 7.7 9.9 9.8 5.5 9.6 9.6 8.6 9.8 9.9 7.9
9.0 7.5 7.7 8.5 9.2 8.7 9.2 9.3 9.2 9.4
女生 9.0 7.6 9.1 9.0 8.0 7.9 8.6 9.2 9.0 9.3
8.2 9.2 8.8 8.5 9.1 8.6 9.0 9.5 9.3 9.1
b.睡眠时长频数分布直方图(分组:5≤x<6,6≤x<7,7≤x<8,8≤x<9,9≤x<10):
c.睡眠时长的平均数、众数、中位数如下:
年级 平均数 众数 中位数
男生 8.8 m 9.2
女生 8.8 9.0 n
根据以上信息,回答下列问题:
(1)补全男生睡眠时长频数分布直方图;
(2)直接写出表中m,n的值;
(3)根据抽样调查情况,可以推断 (填“男生”或“女生”)睡眠情况比较好,理由为 .
31.阅读与思考
下面是小宇学习了“反比例函数的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)满足I的反比例函数关系,它的图象如图所示. 问题一:请写出这个反比例函数的表达式: .
问题二:如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?
方法 分析问题 解答过程
解法一 因为I中电流I≤10,可以得到关于R的不等式并求解 解:∵I= ,且I≤10, ∴ ≤10, ∵R>0, ∴10R≥※,(依据:★) ∴▲.
解法二 因为I,可以求出当电流I=10时相应的R值,并通过反比例函数的增减性求R的取值范围
任务:
(1)问题一中反比例函数的表达式为 ;
(2)问题二中※表示: ,★表示: ,▲表示: ;
(3)完成问题二中解法二的解答过程.
32.如图,点P在正方形ABCD的对角线BD延长线上,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F.
(1)若∠PAD=15°,
①求∠PEF的度数;
②设AB=4,求PE的长;
(2)求证:CEPD.
33.某研究性学习小组通过调查发现,在一节40分钟的课中,学生的注意力会随时间的变化而变化.开始上课时,学生的注意力逐渐集中,中间一段时间保持较为理想的稳定状态,随后开始分散.经试验分析可知,学生的注意力指数y随时间x(分)的变化规律如图所示,其中线段AB的函数表达式为:,线段BC持续的时间恰为10分钟,曲线CD为反比例函数图象的一部分.
(1)求m的值及曲线CD的函数表达式.
(2)若一道数学难题,需要讲解18分钟,为了效果较好,要求学生注意力指数y不低于32,那么老师能否在学生注意力全程达到要求的状态下讲解完这道题?请说明理由.
34.小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛.经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量y(毫克/立方米)与时间x(月)成正比例.施工结束后,y与x成反比例.这两个变量之间的关系如图所示.请根据图中信息,回答下列问题:
(1)施工过程中y关于x的函数解析式是 ;
(2)已知国际上适宜居住的甲醛含量标准为小于或等于0.08毫克/立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以入住?
(3)施工开始后的第2个月底到第4个月底,室内的甲醛含量一直在下降,假设这两个月每个月甲醛含量降低的百分率相同,求这个降低的百分率.(,结果精确到1%)
35.综合与实践
如图1,某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为a m.
【问题提出】
小组同学提出这样一个问题:若a=10,能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设AB为x m,BC为y m.由矩形地块面积为8m2,得到xy=8,满足条件的(x,y)可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为10m,得到2x+y=10,满足条件的(x,y)可看成一次函数y=﹣2x+10的图象在第一象限内点的坐标,同时满足这两个条件的(x,y)就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线l1:y=﹣2x+10的交点坐标为(1,8)和 ,因此,木栏总长为10m时,能围出矩形地块,分别为:AB=1m,BC=8m;或AB= m,BC= m.
(1)根据小颖的分析思路,完成上面的填空.
【类比探究】
(2)若a=6,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
【问题延伸】
当木栏总长为a m时,小颖建立了一次函数y=﹣2x+a.发现直线y=﹣2x+a可以看成是直线y=﹣2x通过平移得到的,在平移过程中,当过点(2,4)时,直线y=﹣2x+a与反比例函数的图象有唯一交点.
(3)请在图2中画出直线y=﹣2x+a过点(2,4)时的图象,并求出a的值.
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=﹣2x+a与图象在第一象限内交点的存在问题”.
(4)若要围出满足条件的矩形地块,且AB和BC的长均不小于1m,请直接写出a的取值范围.
36.已知反比例函数.
(1)若反比例函数的图象经过点(1,3),求k1的值.
(2)若点A(a﹣b,2),B(c﹣b,4)在函数的图象上,比较a,b,c的大小.
(3)反比例函数,如果m≤x≤m+1,且0<m<24,函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,试证明.
37.【方法初探】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.
问题:如图1,在△ABC中,AD⊥BC于点D,若CD=DB+AB,求证:∠B=2∠C.
解题思路:我们可以采用“截长补短法”解决该问题,如图2,辅助线做法在CD上截取DE=DB,连接AE,从而证明出结论.
请你根据上述解题思路,写出证明过程.
【方法应用】如图3,已知:等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD.
【实际应用】如图4,在四边形ABCD中,已知∠BAD=50°,∠D=110°,∠ACD=45°,∠BCA=85°,CE是△ABC的高,AD=12,EB=3,直接写出AE的长 .
一.选择题(共16小题)
1.使得式子有意义的x的取值范围是( )
A.x≥4 B.x>4 C.x≤4 D.x<4
【分析】直接利用二次根式有意义的条件分析得出答案.
【解答】解:使得式子有意义,则:4﹣x>0,
解得:x<4,
即x的取值范围是:x<4.
故选:D.
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形与中心对称图形的概念求解.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.
【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:C.
3.若2<a<3,则( )
A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5
【分析】根据二次根式的性质解答即可.
【解答】解:因为2<a<3,
所以a﹣2﹣(3﹣a)=a﹣2﹣3+a=2a﹣5,
故选:D.
4.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A.中位数是8 B.众数是9 C.平均数是8 D.方差是0
【分析】根据中位数、众数、平均数及方差的计算方法分别求解即可得到答案.
【解答】解:A、按照从小到大的顺序排列为7,7,8,8,9,9,9,10,由中位数的求解方法得到这组数据的中位数为,该选项错误,不符合题意;
B、这组数据中众数为9,该选项正确,符合题意;
C、这组数据平均数为,该选项错误,不符合题意;
D、这组数据的平均数为8.375,则方差为,该选项错误,不符合题意;
故选:B.
5.如图,在菱形ABCD中,E是对角线AC的中点,EF∥CB,交AB于点F,如果EF=3.5,那么菱形ABCD的周长为( )
A.28 B.14 C.7 D.3.5
【分析】根据中位线可得BC长为EF长的2倍,那么菱形ABCD的周长=4BC,问题得解.
【解答】解:∵E是AC的中点,
∴AE=CE,
∵EF∥CB,
∴,
∴AF=BF,
∴EF是△ABC的中位线,
∴BC=2EF=2×3.5=7,
∴菱形ABCD的周长是4×7=28,
故选:A.
6.反比例函数的图象上有A(a,y1),B(2a,y2),C(3a,y3)三点( )
A.若y1<0,则y1﹣y2>y2﹣y3
B.若y1>0,则y1﹣y2>y2﹣y3
C.若y1>0,则|y1﹣y2|<|y2﹣y3|
D.若y1<0,则|y1﹣y2|<|y2﹣y3|
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:分别将点A(a,y1),B(2a,y2),C(3a,y3)代入解析式得:
y1,y2,y3,
∴y1﹣y2,y2﹣y3,
若y1<0,则0,
∴y1﹣y2<y2﹣y3<0,
∴|y1﹣y2|>|y2﹣y3|,
∴A,D均错误;
若y1>0,则0,
∴y1﹣y2>y2﹣y3>0,
∴|y1﹣y2|>|y2﹣y3|,
∴B正确,C错误.
故选:B.
7.若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
【分析】根据一元二次方程的定义及根的判别式即可判断.
【解答】解:∵一元二次方程kx2﹣6x+9=0有实数根,
∴(﹣6)2﹣4×9k≥0,且k≠0,
解得k≤1且k≠0,
故选:D.
8.如图所示,E是菱形ABCD对角线AC上的一点,若BC=6,DE=4,设AE=x,CE=y,则下列代数式为定值的是( )
A.y+x B.xy C.y﹣x D.y2+x2
【分析】连接BD,由菱形的性质推出BD⊥AC,OAAC(x+y),AD=BC=6,求出OE(y﹣x),由勾股定理得到42(y﹣x)2=62(x+y)2,得到xy=20.
【解答】解:连接BD,
∵四边形ABCD是菱形,
∴BD⊥AC,OAAC,AD=BC=6,
∵AE=x,CE=y,
∴AC=x+y,
∴OA(x+y),
∴OE=OA﹣AE(y﹣x),
∵OD2=DE2﹣OE2=AD2﹣AO2,
∴42(y﹣x)2=62(x+y)2,
∴xy=20.
∴代数式为定值的是xy.
故选:B.
9.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
【分析】根据正方形的性质先证明△ABG≌△BCF(AAS),利用其性质结合勾股定理可判断①选项,延长FO交AG于N,证明△AON≌△COF(AAS),利用其性质可证明△FNG为等腰直角三角形,即可判断②.
【解答】解:∵四边形ABCD是正方形,点O是AC的中点,
∴AB=BC=CD=AD=5,∠ABC=∠BCD=∠ADC=∠DAB=90°,
∵AG⊥BE,CF⊥BE,
则AG∥CF,
∴∠AGB=∠BFC=90°,∠ABG+∠EBC=∠BCF+∠EBC=90°,
∴∠ABG=∠BCF,
∴△ABG≌△BCF(AAS),
∴AG=BF,
当AG=4时,,
则FG=BF﹣BG=AG﹣BG=1,故①选项正确;
延长FO交AG于N,
∵AG∥CF,
∴∠OAN=∠OCF,∠ONA=∠OFC,
∵点O为AC的中点,
∴OA=OC,
∴△AON≌△COF(AAS),
∴OF=ON,CF=AN,
∵NG=AG﹣AN,FG=BF﹣BG,
∴NG=FG,即:△FNG为等腰直角三角形,
∴OG平分∠AGE,故②正确.
故选:A.
10.在数学活动课上,老师和同学们判断一个四边形模具是否为菱形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否互相平分且相等
B.测量对角线是否互相平分且垂直
C.测量三条边是否相等
D.测量对角线是否互相垂直且一组邻边相等
【分析】A.菱形的对角线性质是互相垂直且平分,而对角线互相平分且相等是矩形的判定条件.因为矩形的对角线具有互相平分且相等的特点,所以此条件不能判定四边形是菱形,A选项不符合要求.
B.根据平行四边形的判定定理,对角线互相平分的四边形是平行四边形.而菱形是特殊的平行四边形,在平行四边形的基础上,当对角线互相垂直时,就满足了菱形的判定条件,所以如果一个四边形对角线互相平分且垂直,可判定它是菱形,B选项符合要求.
C.菱形的定义是四条边都相等的四边形.仅三条边相等,无法确定第四条边的情况,不能依据此条件判定该四边形是菱形,C选项不符合要求.
D.菱形的判定需要满足特定的条件组合,“对角线互相垂直且一组邻边相等”这种条件组合,不满足菱形判定定理中的任何一条,不能判定该四边形是菱形,D选项不符合要求.
【解答】解:A.对角线互相平分且相等的四边形是矩形,不是菱形,所以该选项错误.
B.:对角线互相平分的四边形是平行四边形,在此基础上,若对角线还互相垂直,根据菱形的判定定理,这个平行四边形就是菱形,所以该选项正确.
C.仅测量三条边相等,不能判定这个四边形是菱形,菱形需要四条边都相等,所以该选项错误.
D.对角线互相垂直且一组邻边相等,不能判定这个四边形是菱形,不满足菱形的判定条件,所以该选项错误.
故选:B.
11.如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关
B.S的值仅与c,k有关
C.S的值仅与k有关
D.S的值与a,b,c,k都有关
【分析】根据题意,先确定各点的坐标,C(b,0),B(b,a),A(0,a),P(c,),F(c,a),利用S△CEF=S△ABC﹣S△AEF﹣S△BCF得到结论即可.
【解答】解:如图,
由条件可知C(b,0),B(b,a),A(0,a),
∵点P在反比例函数(k为常数,k>0)的图象上,且横坐标为c,
∴P(c,),F(c,a),
∴S△AEF AF (a)(ac﹣k),
S△BCF,
S△ABC,
∴S△CEF=S△ABC﹣S△AEF﹣S△BCF,
∴△EFC的面积为S仅与k值有关.
故选:C.
12.折纸不仅具有艺术审美价值,还蕴含着许多数学知识.如图,一张长方形纸片ABCD,点E,F分别是线段AD,BC上的点,先将纸片沿EF折叠,点A,B的对应点分别为点A′,B',A'B'与线段AD交于点G,点H是线段DC上一点,再将纸片沿GH折叠,点D的对应点为点D',点B'恰好在GD'上,若测得∠BFE=66°,则∠DGH的度数是( )
A.21° B.26° C.33° D.42°
【分析】由矩形的性质得AD∥BC,∠A=90°,因为∠BFE=66°,所以∠DEF=∠BFE=66°,∠AEF=114°,由折叠得∠A′=∠A=90°,∠A′EF=∠AEF=114°,则∠A′EG=∠A′EF﹣∠DEF=48°,求得∠DGB′=∠EGA′=42°,而点B′在GD′上,所以∠DGD′=42°,则∠DGH∠DGD′=21°,于是得到问题的答案.
【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∵∠BFE=66°,
∴∠DEF=∠BFE=66°,∠AEF=180°﹣∠BFE=114°,
由折叠得∠A′=∠A=90°,∠A′EF=∠AEF=114°,∠DGH=∠D′GH,
∴∠A′EG=∠A′EF﹣∠DEF=114°﹣66°=48°,
∴∠DGB′=∠EGA′=90°﹣∠A′EG=42°,
∵点B′在GD′上,
∴∠DGD′=∠DGB′=42°,
∴∠DGH∠DGD′=21°,
故选:A.
13.如图,在△ABC中,∠C=90°,∠B=32°,E,F分别在边BC,AB上,将△BEF沿着EF折叠,得到△B'EF,B′E与AB交于G.当B′E∥AC时,∠AFB'的度数是( )
A.25° B.26° C.30° D.32°
【分析】由∠C=90°,∠B=32°,求得∠A=58°,由B′E∥AC,得∠AGB′=∠A=58°,由折叠得∠B′=∠B=32°,则58°=∠AFB′+32°,求得∠AFB′=26°,于是得到问题的答案.
【解答】解:∵∠C=90°,∠B=32°,
∴∠A=90°﹣∠B=58°,
∵B′E∥AC,
∴∠AGB′=∠A=58°,
∵将△BEF沿着EF折叠,得到△B'EF,
∴∠B′=∠B=32°,
∵∠AGB′=∠AFB′+∠B′,
∴58°=∠AFB′+32°,
∴∠AFB′=26°,
故选:B.
14.如图,是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,连结AE,DE,若AD=AE,,则正方形ABCD的边长是( )
A. B. C. D.
【分析】由全等三角形的性质以及等腰三角形的性质可得△DEH是等腰直角三角形,根据勾股定理可得DH=HE=2,再由勾股定理,即可求解.
【解答】解:∵赵爽弦图的示意图由四个全等的直角三角形拼接成一个正方形ABCD,
∴BE=CH=DG,GH=EH=EF=FG,AF⊥BE,CH⊥DG,AB=AD=AE,
∴BF=EF=EC=EH=DH,
∴△DEH是等腰直角三角形,
由勾股定理得:,
∵,
∴HE=DH=2,
∴CH=4,
由勾股定理得:,
∴正方形ABCD的边长是,
故选:D.
15.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,射线EG与BC的延长线相交于点P.若∠P=30°,则的值是( )
A. B.3 C. D.
【分析】作CM⊥PG于点M,GN⊥PB于点N,设CM=x,在Rt△PCM中,求得CP=2x,,在Rt△CGM中,求得,,在Rt△PNG中,求得,,再证明∠GCN∽∠BCG,求得,据此求解即可.
【解答】解:作CM⊥PG于点M,GN⊥PB于点N,
设CM=x,
∴△PCM是直角三角形,
∵∠P=30°,
∴CP=2CM=2x,,
∵四边形EFGH是正方形,
∴∠FGC=∠FGH=90°,∠CGM=∠EGH=45°,
在Rt△CGM中,∠CGM=45°,
∴CM=GM=x,
∴,,
在Rt△PNG中,∠P=30°,
∴,,
∴,
∵∠GNC=∠BGC=90°,∠GCN=∠BCG,
∴∠GCN∽∠BCG,
∴,
∴,
∴,
∴,
故选:A.
16.“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
【分析】由全等三角形的性质可得EF=EH,先对Rt△EFH运用勾股定理求出EF,再对Rt△DEF运用勾股定理求出DE=AF,则AE即可求得,最后对Rt△AED运用勾股定理即可求解.
【解答】解:∵大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成,
∴AF=DE,DH=AE,∠AED=∠DEF=90°,
∴AF﹣AE=DE﹣DH,
∴EF=EH,
在直角三角形EFH中,,
由勾股定理得:EF2+EH2=HF2,
∴EF=EH=2,
在直角三角形DEF中,,
由勾股定理得:,
∴AE=AF﹣FE=5﹣2=3,
在直角三角形ADE中,由勾股定理得:,
故选:D.
二.填空题(共8小题)
17.如图,在 ABCD中,∠ABC=60°,AB=6,BC=10,点E是边BC上一点,将△ABE沿AE折叠后,点B的对应点为点F.
(1)如图1,连接DE,若点F恰好落在边DE上.则BE的长为 13 .
(2)如图2,连接BD,若EF∥BD,则BE的长为 4 .
【分析】(1)过点D作DH⊥BC,交BC的延长线于点H,利用轴对称的性质得到∠AEB=∠AED,利用平行四边形的性质,平行线的性质和等腰三角形的判定定理求出AD=DE=10,利用平行四边形的性质和含30°角的直角三角形的性质求得线段CH,DH,利用勾股定理求得EH,进而求得CE,则BE=BC﹣EC;
(2)延长EF交AD的延长线于点G,过点G作GH⊥BC于点H,过点D作DK⊥BC于点K,利用平行四边形的判定与性质得到BE=DG,设BE=DG=x,利用矩形的判定与性质得到HK=DG=x,GH=DK,再利用勾股定理和(1)的结论解答即可得出结论.
【解答】解:(1)过点D作DH⊥BC,交BC的延长线于点H,如图1,
∵四边形ABCD是平行四边形,
∴AD=BC=10,DC=AB=6,AD∥BC,DC∥AB,
∴∠DAE=∠AEB,∠DCH=∠ABC=60°,
由折叠得:△ABE≌△AFE,
∴∠AEB=∠AED,
∴∠AED=∠DAE,
∴AD=DE=10,
在Rt△DCH中,CHDC=3,DHDC=3,
在Rt△DEH中,EH,
∴CE=EH﹣CH3,
∴BE=BC﹣EC=10﹣(3)=13,
故答案为:13;
(2)延长EF交AD的延长线于点G,过点G作GH⊥BC于点H,过点D作DK⊥BC于点K,如图2,
∵BE∥AD,EF∥BD,
∴四边形BEGD为平行四边形,
∴BE=DG.
∴设BE=DG=x,则EC=10﹣x,
∵DK⊥BC,GH⊥BC,AD∥BC,
∴四边形DKHG为矩形,
∴HK=DG=x,GH=DK.
由(1)知:DK=3,CK=3,
∴EH=EC+CK+KH=10﹣x+3+x=13,
在Rt△EHG中,EG14,
由折叠得:∠AEB=∠AEG,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠AEG=∠DAE,
∴EG=AG=14,
∴BE=DG=AG﹣AD=14﹣10=4,
故答案为:4.
18.计算6的结果是 4 .
【分析】先进行开方运算,再合并同类二次根式即可.
【解答】解:原式=264
=224
=4.
故答案为:4.
19.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 72° .
【分析】先根据正五边形的性质得出正五边形内角的度数,再根据等腰三角形的性质求出∠BCA的度数,进而可得出结论.
【解答】解:∵五边形ABCDE是正五边形,
∴其每个内角为108°,且AB=BC,
∴△ABC是等腰三角形,
∴∠BCA=(180°﹣108°)÷2=36°,
∴∠ACD=∠BCE﹣∠BCA=108°﹣36°=72°.
故答案为:72°
20.对于字母m、n,定义新运算m☆n=mn﹣m﹣n,若方程x2+3x+1=0的解为a、b,则a☆b+2的值为 6. .
【分析】判断出a+b=﹣3,ab=1,再根据新定义计算即可.
【解答】解:∵方程x2+3x+1=0的解为a、b,
∴a+b=﹣3,ab=1,
∴a☆b+2=ab﹣a﹣b+2=1+3+2=6.
故答案为:6.
21.若α,β是一元二次方程x2﹣3x﹣8=0的两个根,则α2﹣4α﹣β的值为 5 .
【分析】将α2﹣4α﹣β化为α2﹣3α﹣(α+β)分别求出α2﹣3α=8、α+β=3即可求得答案.
【解答】解:∵α、β是一元二次方程x2﹣3x﹣8的两个根,
∴α2﹣3α﹣8=0,
∴α2﹣3α=8,
∵α+β=3,
∴α2﹣4α﹣β=α2﹣3α﹣α﹣β=α2﹣3α﹣(α+β)=8﹣3=5.
故答案为:5.
22.某社团统计成员一周的活动时间情况,列出了方差的计算公式:S2[2×(2)2+4×(3)2+3×(4)2+(8)2],则的值是 3.6 .
【分析】根据方差的计算公式得出这组数据为2、2、3、3、3、3、4、4、4、8,再根据平均数的定义列式计算即可.
【解答】解:由题意知,这组数据为2、2、3、3、3、3、4、4、4、8,
所以这组数据的平均数3.6,
故答案为:3.6.
23.已知点(﹣1,2)在反比例函数的图象上,当y≤2时,x的取值范围是 x≤﹣1或x>0 .
【分析】根据点(﹣1,2)在反比例函数的图象上,求出k的值,得到反比例函数解析式,再根据反比例函数的性质求解即可.
【解答】解:∵点(﹣1,2)在反比例函数的图象上,
∴k=﹣1×2=﹣2,
∴函数解析式为y,
∴图象位于二、四象限,
在每个象限内,y随x的增大而增大,
当y=2时,x=﹣1,
则当y≤2时,x≤﹣1或x>0.
故答案为:x≤﹣1或x>0.
24.如图,正方形ABCD的边长为1,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②FE平分∠AFG;③BE+DG=EG;④△EAF的面积的最大值是;其中正确的结论是 ①③ .
【分析】在BC上截取BH=BE,连接EH,如图:根据等腰直角三角形的性质得到EHBE,求得AF=EH,根据全等三角形的性质得到∠AEF=∠ECH,推出△ECF是等腰直角三角形,得到∠ECF=∠EFC=45°,故①正确;得到∠BEH=45°,求得∠AFE≠∠EFC,推出FE不平分∠AFG,故②错误,延长AD到H,使得DH=BE,根据全等三角形的性质得到∠ECB=∠DCH,EG=GH,得到EG=BE+DG,故③正确,设BE=x,则AE=1﹣x,AFx,根据三角形的面积公式和二次函数的性质即可得到结论.
【解答】解:在BC上截取BH=BE,连接EH,如图1:
∵BE=BH,∠EBH=90°,
∴EHBE,
∵AFBE,
∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,
∴△FAE≌△EHC(SAS),
∴∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,
∴∠AEF+∠CEB=90°,
∴∠FEC=90°,
∴△ECF是等腰直角三角形,
∴∠ECF=∠EFC=45°,故①正确;
∵∠B=90°,
∴∠BEH=45°,
∵∠BEC<90°,
∴∠CEH<45°,
∴∠AFE<45°,
∴∠AFE≠∠EFC,
∴FE不平分∠AFG,故②错误,
延长AD到H,使得DH=BE,如图2:
可得△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,
∴∠ECH=∠BCD=90°,
∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,
∴△GCE≌△GCH(SAS),
∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③正确,
设BE=x,则AE=1﹣x,AFx,
∴S△AEF (1﹣x)×xx2x(x2﹣x)(x)2,
∵0,
∴x时,△AEF的面积的最大值为.故④错误,
故答案为:①③.
三.解答题(共13小题)
25.我们常常把一张A4纸通过折叠的方式得到它的对角线,如图1.折纸活动中,通过点与点重合或边与边重合,才能得到精准的折叠.现有一张A4纸张(矩形ABCD),如图2,设折叠后B'C边与AD边重叠的点为E.
(1)请用尺规作图的方式在图2中画出点E.
(2)根据以上折纸活动的提示,描述折出A4纸(矩形ABCD)对角线的两个步骤.
【分析】(1)分别以A,C为圆心,AB,BC为半径作弧,两弧交于点B′,连接AB′,CB′,CB′交AD于点E;
(2)步骤一:点A,点C两点重合,得到折痕EE′;
步骤二:点E,点E′重合可以折出A4纸(矩形ABCD)对角线AC.
【解答】解:(1)如图2中,点E即为所求;
(2)如图3中,步骤一:点A,点C两点重合,得到折痕EE′;
步骤二:点E,点E′重合可以折出A4纸(矩形ABCD)对角线AC.
26.在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
【分析】(1)易得AC=5,所以AC1=AC=5,再利用勾股定理求解即可;
(2)连结BD交AC于点O,证OH为△BDD1的中位线,即可得证;
(3)连接PC1,证∠BC1P=90°,在Rt△AD1B中,BD1,所以BC1=4,再利用勾股定理建立方程求解即可.
【解答】(1)解:在矩形ABCD中,AB=4,BC=3,
∴,
∵△ACD、△ACD关于直线AP对称,
∴AC1=AC=5,
∴BC=AC﹣AB=1,
在Rt△BCC1中,由勾股定理得,
,
∴CC1的长为;
(2)证明:连结BD交AC于点O,
∵ABCD为矩形,
∴OB=OD
∵D,D1关于AC对称,
∴AC垂直平分DD1,
∴H为DD1的中点,
∴OH为△BDD1的中位线,
∴OH∥BD1,
∵AC⊥DD1,
∴∠DHO=90°,
∵OH∥BD,
∴∠BD1D=∠DHO=90°,
∴DD⊥BD1;
(3)解:连接PC1,
∵△ACD、△AC1D1关于直线AP对称,
∴AD=AD,CD=CD,∠ACD=∠AC1B∠ACP=∠AC1PPC=PC1,∠ADC=∠AC1C=90°,
∵∠ACD+∠ACP=90°
∴∠AC1B+∠AC1P=90°,
即∠BC1P=90°,
当直线C1D1经过点B时,
在Rt△AD1B中,BD1,
∴BC1=C1D1﹣BD1=4,
在Rt△BC1P中,,
∴,,
∴.
27.定义:有一组邻边垂直且对角线相等的四边形为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 正方形或矩形 .
(2)如图1,在3×3方格纸中,A,B,C在格点上,请画出两个符合条件的不全等的垂等四边形,使AC,BD是对角线,点D在格点上.
(3)如图2,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,AE=AF=CG且∠DGC=∠DEG,求证:四边形DEFG是垂等四边形.
【分析】(1)根据定义易得解;
(2)①画一个符合题意得矩形 ABCD,②根据BC=5,可以找点D使CD=5,并且满尊BD=AC即可得解;
(3)先证△ADF≌△CDG(SAS),可得DF=DG,再导角证DG=EG,进而得证.
【解答】(1)解:由题意可知:正方形,矩形,
故答案为:正方形或矩形;
(2)解:如图1中,四边形ABCD即为所求.
(3)证明:在正方形ABCD中,
∵AF=CG,AB=BC,
∴FB=BG,
∴∠AEF=∠AFE=45°,∠BFG=∠BGF=45°,
∴∠EFG=90°,
∵∠A=∠C=90°,DA=DC,AF=CG,
∴△ADF≌△CDG(SAS),
∴DF=DG,
∵AD∥CB,
∴∠EDG=∠DGC,
∵∠DGC=∠DEG,
∴∠GDE=∠GED,
∴DG=EG,
∴DF=EG,
∴四边形DEFG是垂等四边形.
28.计算题:
(1);
(2).
【分析】(1)根据负整数指数幂,零指数幂,绝对值,分母有理化等知识计算即可;
(2)根据根式的乘法法则计算即可.
【解答】解:(1)原式=﹣3﹣1+2
=﹣3﹣1+22
=﹣2;
(2)原式=24
=44
=122.
29.已知关于x的一元二次方程x2﹣(2m+1)x+m﹣2=0.
(1)求证:不论m取何值,方程总有两个不相等的实数根;
(2)若方程有两个实数根为x1,x2,且x1+x2+3x1x2=1,求m的值.
【分析】(1)根据根的判别式得出Δ=[﹣(2m+1)]2﹣4×1×(m﹣2)=4m2+9>0,据此可得答案;
(2)根据根与系数的关系得出x1+x2=2m+1,x1x2=m﹣2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【解答】(1)证明:∵Δ=[﹣(2m+1)]2﹣4×1×(m﹣2)
=4m2+4m+1﹣4m+8
=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根;
(2)解:由根与系数的关系,得x1+x2=2m+1,x1x2=m﹣2,
由x1+x2+3x1x2=1,得2m+1+3(m﹣2)=1,
解得m.
30.2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,该意见对学生睡眠时间提出了新的要求.为了了解某校初二年级学生的睡眠时长,随机抽取了初二年级男生和女生各20位,对其同一天的睡眠时长进行调查,并对数据进行收集、整理、描述和分析.下面给出了相关信息.
a.睡眠时长(单位:小时):
男生 7.7 9.9 9.8 5.5 9.6 9.6 8.6 9.8 9.9 7.9
9.0 7.5 7.7 8.5 9.2 8.7 9.2 9.3 9.2 9.4
女生 9.0 7.6 9.1 9.0 8.0 7.9 8.6 9.2 9.0 9.3
8.2 9.2 8.8 8.5 9.1 8.6 9.0 9.5 9.3 9.1
b.睡眠时长频数分布直方图(分组:5≤x<6,6≤x<7,7≤x<8,8≤x<9,9≤x<10):
c.睡眠时长的平均数、众数、中位数如下:
年级 平均数 众数 中位数
男生 8.8 m 9.2
女生 8.8 9.0 n
根据以上信息,回答下列问题:
(1)补全男生睡眠时长频数分布直方图;
(2)直接写出表中m,n的值;
(3)根据抽样调查情况,可以推断 男生 (填“男生”或“女生”)睡眠情况比较好,理由为 睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生 .
【分析】(1)求出男生8≤x<9的频数,然后即可将频数分布直方图补充完整;
(2)根据众数和中位数的定义即可得到m,n的值;
(3)根据统计量的意义判断,并说明理由即可.
【解答】解:(1)男生8≤x<9的频数为20﹣1﹣4﹣12=3,
补全男生睡眠时长频数分布直方图如下:
(2)∵男生睡眠时长中:9.2小时出现3次,是出现次数最多的数据,
∴m=9.2,
∵女生睡眠时长中位数是数据由小到大排列第10,第11个数据的平均数,由数据可知,第10,第11个数据分别为:9,9,
∴n=(9+9)÷2=9;
(3)根据题目中的信息可知,男生睡眠情况比较好,
理由为:睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生.
故答案为:男生,睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生.
31.阅读与思考
下面是小宇学习了“反比例函数的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)满足I的反比例函数关系,它的图象如图所示. 问题一:请写出这个反比例函数的表达式: I .
问题二:如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?
方法 分析问题 解答过程
解法一 因为I中电流I≤10,可以得到关于R的不等式并求解 解:∵I= ,且I≤10, ∴ ≤10, ∵R>0, ∴10R≥※,(依据:★) ∴▲.
解法二 因为I,可以求出当电流I=10时相应的R值,并通过反比例函数的增减性求R的取值范围
任务:
(1)问题一中反比例函数的表达式为 I ;
(2)问题二中※表示: 36 ,★表示: 不等式的两边同时乘(或除以)同一个正数,不等号的方向不变 ,▲表示: R≥3.6 ;
(3)完成问题二中解法二的解答过程.
【分析】(1)根据函数图象上点的坐标,利用反比例函数图象上点的坐标特征,即可求出U值,进而可得出反比例函数的表达式;
(2)由I,且I≤10,可得出10,结合R>0,即可求出R的取值范围;
(3)利用反比例函数图象上点的坐标特征,可求出当I=10时R的值,由36>0且R>0,利用反比例函数的性质,可得出I随R的增大而减小,再结合I≤10,即可求出R的取值范围.
【解答】解:(1)∵反比例函数I的图象过点(9,4),
∴4,
∴U=36,
∴反比例函数的表达式为I.
故答案为:I;
(2)∵I,且I≤10,
∴10,
∵R>0,
∴10R≥36(不等式的两边同时乘(或除以)同一个正数,不等号的方向不变),
∴R≥3.6.
故答案为:,,36,不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,R≥3.6;
(3)解法二:当I=10时,10,
解得:R=3.6,
∵36>0,且R>0,
∴I随R的增大而减小,
又∵I≤10,
∴R≥3.6.
32.如图,点P在正方形ABCD的对角线BD延长线上,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F.
(1)若∠PAD=15°,
①求∠PEF的度数;
②设AB=4,求PE的长;
(2)求证:CEPD.
【分析】(1)①根据正方形性质得∠ABP=∠ADB=∠CBP=45°,进而得∠APD=30°,再根据PE⊥PA,EF⊥BP得∠PEF=∠APD=30°;
②在FE上截取FG=FP,连接PG,BG,连接CG,则△PFG是等腰直角三角形,进而得∠FPG=45°,再证明△FBE是等腰直角三角形得BF=EF,∠FEB=45°,由此可判定△BFG和△EFP全等,则∠GBF=∠PEF=∠APD=30°,解得BG∥AP,再根据∠FPG=∠ABP=45°得AB∥PG,由此得四边形ABGP是平行四边形,则PG=AB=4,在Rt△PFG,由勾股定理得FPPG,然后在Rt△PEF中,根据∠PEF=30°即可得出PE的长;
(2)先证明四边形DCGP是平行四边形,则PD=CG,∠DCG=∠FPG=45°,进而得∠GCE=∠FEB=45°,则△GCE是等腰直角三角形,由勾股定理得CECG,由此即可得出结论.
【解答】(1)①解:∵四边形ABCD是正方形,点P在对角线BD的延长线上,
∴∠ABP=∠ADB=∠CBP=45°,
∵∠ADP是△ADP的外角,
∴∠ADP=∠PAD+∠APD,
∵∠PAD=15°,
∴45°=15°+∠APD,
∴∠APD=30°,
∵PE⊥PA,EF⊥BP,
∴∠APE=90°,∠PFE=90°,
∴∠APD+∠EPF=90°,∠PEF+∠EPF=90°,
∴∠PEF=∠APD=30°;
②解:在FE上截取FG=FP,连接PG,BG,连接CG,如图所示,
∵EF⊥BP,
∴∠BFG=∠EFP=90°,
∴△PFG是等腰直角三角形,
∴∠FPG=45°,
∵∠CBP=45°,EF⊥BP,
∴△FBE是等腰直角三角形,
∴BF=EF,∠FEB=45°,
在△BFG和△EFP中,
,
∴△BFG≌△EFP(SAS),
∴∠GBF=∠PEF=30°,
∴∠GBF=∠APD=30°,
∴BG∥AP,
又∵∠FPG=∠ABP=45°,
∴AB∥PG,
∴四边形ABGP是平行四边形,
∴PG=AB=4,
在等腰Rt△PFG中,
由勾股定理得:PGFP,
∴FPPG,
在Rt△PEF中,∠PEF=30°,
∴PE=2FP;
(2)证明:∵四边形ABCD是正方形,
∴AB=DC,AB∥DC,∠DCB=∠DCE=90°,
由(1)可知:四边形ABGP是平行四边形,
∴AB∥PG,AB=PG,
∴DC∥PG,DC=PG,
∴四边形DCGP是平行四边形,
∴PD=CG,∠DCG=∠FPG=45°,
∴∠GCE=∠DCE﹣∠DCG=45°,
∴∠GCE=∠FEB=45°,
∴△GCE是等腰直角三角形,
∴CG=EG,
由勾股定理得:CECG,
∵PD=CG,
∴CEPD.
33.某研究性学习小组通过调查发现,在一节40分钟的课中,学生的注意力会随时间的变化而变化.开始上课时,学生的注意力逐渐集中,中间一段时间保持较为理想的稳定状态,随后开始分散.经试验分析可知,学生的注意力指数y随时间x(分)的变化规律如图所示,其中线段AB的函数表达式为:,线段BC持续的时间恰为10分钟,曲线CD为反比例函数图象的一部分.
(1)求m的值及曲线CD的函数表达式.
(2)若一道数学难题,需要讲解18分钟,为了效果较好,要求学生注意力指数y不低于32,那么老师能否在学生注意力全程达到要求的状态下讲解完这道题?请说明理由.
【分析】(1)把y=40,x=m代入yx+15得40m+15,解方程得到m=10,求得B(10,40),得到C(20,40),设反比例函数的解析式为y,把C(20,40)代入y,解方程即可得到结论;
(2)分别求出注意力指数为32时的两个时间,再将两时间之差和18比较,大于18则能讲完,否则不能.
【解答】解:(1)把y=40,x=m代入yx+15得40m+15,
解得m=10,
∴B(10,40),
∵线段BC持续的时间恰为10分钟,
∴C(20,40),
设反比例函数的解析式为y,
把C(20,40)代入y得40得k=800,
∴曲线CD的函数表达式为y;
(2)令y=32,
∴32x+15,
∴x=6.8,
令y=32,
∴32,
∴x25,
∵25﹣6.8=18.2>18,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
34.小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛.经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量y(毫克/立方米)与时间x(月)成正比例.施工结束后,y与x成反比例.这两个变量之间的关系如图所示.请根据图中信息,回答下列问题:
(1)施工过程中y关于x的函数解析式是 y=1.25x(0≤x≤0.8) ;
(2)已知国际上适宜居住的甲醛含量标准为小于或等于0.08毫克/立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以入住?
(3)施工开始后的第2个月底到第4个月底,室内的甲醛含量一直在下降,假设这两个月每个月甲醛含量降低的百分率相同,求这个降低的百分率.(,结果精确到1%)
【分析】(1)施工过程中y与x成正比例函数,设出正比例函数解析式,把(0.8,1)代入即可求得相应的函数解析式;
(2)当x>0.8时,y与x成反比例函数解析式,设出反比例函数解析式,把(0.8,1)代入即可求得相应的函数解析式,进而取y=0.08,得到相应的x的值即为可以入住的时间;
(3)取x=2,x=4,得到相应的y的值,进而设降低的百分率为m,根据2月底的甲醛含量(1﹣降低的百分率)2=4月底的甲醛含量,计算后取得合适的解即可.
【解答】解:(1)当0≤x≤0.8时,设y=kx,
∵经过点(0.8,1),
∴0.8k=1,
解得:k=1.25,
∴y=1.25x;
∴施工过程中y关于x的函数解析式为:y=1.25x(0≤x≤0.8).
故答案为:y=1.25x(0≤x≤0.8);
(2)当x>0.8时,设y,
∵经过点(0.8,1),
∴a=0.8,
∴y,
当y=0.08时,x=10.
答:小明一家从施工开始计算,至少经过10个月才可以入住;
(3)当x=2时,y=0.4,
当x=4时,y=0.2.
设这两个月降低的百分率为m,
0.4(1﹣m)2=0.2,
(1﹣m)2,
解得:m1=1(不合题意,舍去),m2=10.293≈29.3%.
答:降低的百分率约为29.3%.
35.综合与实践
如图1,某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为a m.
【问题提出】
小组同学提出这样一个问题:若a=10,能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设AB为x m,BC为y m.由矩形地块面积为8m2,得到xy=8,满足条件的(x,y)可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为10m,得到2x+y=10,满足条件的(x,y)可看成一次函数y=﹣2x+10的图象在第一象限内点的坐标,同时满足这两个条件的(x,y)就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线l1:y=﹣2x+10的交点坐标为(1,8)和 (4,2) ,因此,木栏总长为10m时,能围出矩形地块,分别为:AB=1m,BC=8m;或AB= 4 m,BC= 2 m.
(1)根据小颖的分析思路,完成上面的填空.
【类比探究】
(2)若a=6,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
【问题延伸】
当木栏总长为a m时,小颖建立了一次函数y=﹣2x+a.发现直线y=﹣2x+a可以看成是直线y=﹣2x通过平移得到的,在平移过程中,当过点(2,4)时,直线y=﹣2x+a与反比例函数的图象有唯一交点.
(3)请在图2中画出直线y=﹣2x+a过点(2,4)时的图象,并求出a的值.
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=﹣2x+a与图象在第一象限内交点的存在问题”.
(4)若要围出满足条件的矩形地块,且AB和BC的长均不小于1m,请直接写出a的取值范围.
【分析】(1)观察图象或联立解方程组得到另一个交点坐标为(4,2);
(2)观察图象得到l2 与函数 图象没有交点,所以不能围出;
(3)平移直线y=﹣2x通过(2,4),将点(2,4)代入y=﹣2x+a,解得a=8;
(4)AB和BC的长均不小于1m,所以1≤x≤8,直线y=﹣2x+a在l3、l4之间移动,可得求a的范围.
【解答】解:(1)将反比例函数y与直线l1:y=﹣2x+10联立得:
,
∴2x+10,
整理得:x2﹣5x+4=0,
解得:x1=1,x2=4,
∴另一个交点坐标为(4,2),
∵AB为x m,BC为y m,
∴AB=4,BC=2.
故答案为:(4,2);4;2;
(2)a=6,不能围出矩形地块;理由如下:
y=﹣2x+6的图象,如图中直线l2所示:
∵l2 与函数 图象没有交点,
∴不能围出面积为8m2的矩形;
(3)如图中直线l3所示:
将点(2,4)代入y=﹣2x+a得:4=﹣2×2+a,
解得a=8.
(4)∵AB和BC的长均不小于1m,
∴x≥1,y≥1,
∴1,
∴x≤8,
∴1≤x≤8,
如图所示,直线y=﹣2x+a在l4、l3之间移动,
把(8,1)代入y=﹣2x+a得a=17,
∴8≤a≤17.
36.已知反比例函数.
(1)若反比例函数的图象经过点(1,3),求k1的值.
(2)若点A(a﹣b,2),B(c﹣b,4)在函数的图象上,比较a,b,c的大小.
(3)反比例函数,如果m≤x≤m+1,且0<m<24,函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,试证明.
【分析】(1)将点(1,3)坐标代入求出k1即可;
(2)根据反比例函数图象上点的坐标特征及反比例函数性质解答即可;
(3)由反比例函数的性质可得y2的最大值为,最小值为,y1的最大值为,最小值为,由题意列出两个方程,即可求解.
【解答】(1)解:将点(1,3)坐标代入得:3,
解得:k1=3,
(2)解:∵中k1>0,
∴反比例函数图象分布在第一三象限,y随x的增大而减小,
∵2<4,
∴a﹣b>c﹣b,a﹣b>0,c﹣b>0,
∴a>c>b;
(3)证明:∵反比例函数,如果m≤x≤m+1,且0<m<24,
∴y2随x的增大而增大,则y2的最大值为,最小值为,
∵反比例函数.如果m≤x≤m+1,且0<m<24,
∴y1随x的增大而减小,则y1的最大值为,最小值为,
∵函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,
∴5,4.8,
∴(m+1)k1﹣k2m=5m(m+1)①,mk1﹣(m+1)k2=4.8m(m+1)②,
∴①﹣②得:k1+k2=0.2m(m+1),
∴k1+k2.
37.【方法初探】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.
问题:如图1,在△ABC中,AD⊥BC于点D,若CD=DB+AB,求证:∠B=2∠C.
解题思路:我们可以采用“截长补短法”解决该问题,如图2,辅助线做法在CD上截取DE=DB,连接AE,从而证明出结论.
请你根据上述解题思路,写出证明过程.
【方法应用】如图3,已知:等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD.
【实际应用】如图4,在四边形ABCD中,已知∠BAD=50°,∠D=110°,∠ACD=45°,∠BCA=85°,CE是△ABC的高,AD=12,EB=3,直接写出AE的长 15 .
【分析】【方法初探】根据已知可得AD是BE的垂直平分线,从而可得AB=AE,进而可得∠B=∠AEB,然后结合已知AB+BD=DC,可得AB=EC,从而可得AE=EC,进而可得∠C=∠EAC,最后利用三角形的外角性质可得∠AEB=2∠C,即可解答;
【方法应用】先证明△ABD≌△AHD得到AH=AB,BD=HD,再证明△CDH是等腰直角三角形,推出BD=HC,据此根据线段的和差关系即可证明结论;
【实际应用】由三角形内角和定理可得∠DAC=25°,证明△DAC≌△FAC(SAS)得出∠AFC=∠D=110°,再证明△CEF≌△CEB(AAS)得出EF=BE,求出BF=2BE=6,即可得解.
【解答】【方法初探】证明:如图2,在DC上截取DE=DB,连接AE,
∵AD⊥BC,BD=DE,
∴AD是BE的垂直平分线,
∴AB=AE,
∴∠B=∠AEB,
∵AB+BD=DC,DE+EC=DC,
∴AB=EC,
∴AE=EC,
∴∠C=∠EAC,
∵∠AEB=∠C+∠EAC,
∴∠AEB=2∠C,
∴∠B=2∠C;
【方法应用】证明:如图所示,过点D作DH⊥AC于H,
∴∠AHD=90°=∠B,
∵AD是角平分线,
∴∠BAD=∠HAD,
又∵AD=AD,
∴△ABD≌△AHD(AAS),
∴AH=AB,BD=HD,
∵△ABC是等腰直角三角形,
∴∠C=45°,
∴△CDH是等腰直角三角形,
∴HD=HC,
∴BD=HC,
∵AC=AH+CH,
∴AC=AB+BD;
【实际应用】解:在AE上截取AF=AD,连接CF,
由题意可得:
∴∠DAC=180°﹣∠D﹣∠ACD=25°,
∴∠FAC=∠BAD﹣∠DAC=25°,
∴∠DAC=∠FAC=25°,
∵AC=AC,
在△DAC和△FAC中,
,
∴△DAC≌△FAC(SAS),
∴∠AFC=∠D=110°,
∴∠CFE=180°﹣∠AFC=70°,
∴∠B=180°﹣∠ACB﹣∠FAC=70°,
∴∠B=∠CFE,
∵CE⊥AB,
∴∠CEF=∠CEB=90°,
∴CE=CE,
在△CEF和△CEB中,
,
∴△CEF≌△CEB(AAS),
∴EF=BE,
∴BF=2BE=6,
∴AB=AF+BF=12+6=18,
∴AE=AB﹣BE=18﹣3=15.
故答案为:15.
浙江省杭州市2024—2025学年度八年级下学期期末训练卷
一.选择题(共16小题)
1.使得式子有意义的x的取值范围是( )
A.x≥4 B.x>4 C.x≤4 D.x<4
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
3.若2<a<3,则( )
A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5
4.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A.中位数是8 B.众数是9 C.平均数是8 D.方差是0
5.如图,在菱形ABCD中,E是对角线AC的中点,EF∥CB,交AB于点F,如果EF=3.5,那么菱形ABCD的周长为( )
A.28 B.14 C.7 D.3.5
6.反比例函数的图象上有A(a,y1),B(2a,y2),C(3a,y3)三点( )
A.若y1<0,则y1﹣y2>y2﹣y3
B.若y1>0,则y1﹣y2>y2﹣y3
C.若y1>0,则|y1﹣y2|<|y2﹣y3|
D.若y1<0,则|y1﹣y2|<|y2﹣y3|
7.若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
8.如图所示,E是菱形ABCD对角线AC上的一点,若BC=6,DE=4,设AE=x,CE=y,则下列代数式为定值的是( )
A.y+x B.xy C.y﹣x D.y2+x2
9.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
10.在数学活动课上,老师和同学们判断一个四边形模具是否为菱形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否互相平分且相等
B.测量对角线是否互相平分且垂直
C.测量三条边是否相等
D.测量对角线是否互相垂直且一组邻边相等
11.如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关
B.S的值仅与c,k有关
C.S的值仅与k有关
D.S的值与a,b,c,k都有关
12.折纸不仅具有艺术审美价值,还蕴含着许多数学知识.如图,一张长方形纸片ABCD,点E,F分别是线段AD,BC上的点,先将纸片沿EF折叠,点A,B的对应点分别为点A′,B',A'B'与线段AD交于点G,点H是线段DC上一点,再将纸片沿GH折叠,点D的对应点为点D',点B'恰好在GD'上,若测得∠BFE=66°,则∠DGH的度数是( )
A.21° B.26° C.33° D.42°
13.如图,在△ABC中,∠C=90°,∠B=32°,E,F分别在边BC,AB上,将△BEF沿着EF折叠,得到△B'EF,B′E与AB交于G.当B′E∥AC时,∠AFB'的度数是( )
A.25° B.26° C.30° D.32°
14.如图,是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,连结AE,DE,若AD=AE,,则正方形ABCD的边长是( )
A. B. C. D.
15.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,射线EG与BC的延长线相交于点P.若∠P=30°,则的值是( )
A. B.3 C. D.
16.“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
二.填空题(共8小题)
17.如图,在 ABCD中,∠ABC=60°,AB=6,BC=10,点E是边BC上一点,将△ABE沿AE折叠后,点B的对应点为点F.
(1)如图1,连接DE,若点F恰好落在边DE上.则BE的长为 .
(2)如图2,连接BD,若EF∥BD,则BE的长为 .
18.计算6的结果是 .
19.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 .
20.对于字母m、n,定义新运算m☆n=mn﹣m﹣n,若方程x2+3x+1=0的解为a、b,则a☆b+2的值为 .
21.若α,β是一元二次方程x2﹣3x﹣8=0的两个根,则α2﹣4α﹣β的值为 .
22.某社团统计成员一周的活动时间情况,列出了方差的计算公式:S2[2×(2)2+4×(3)2+3×(4)2+(8)2],则的值是 .
23.已知点(﹣1,2)在反比例函数的图象上,当y≤2时,x的取值范围是 .
24.如图,正方形ABCD的边长为1,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②FE平分∠AFG;③BE+DG=EG;④△EAF的面积的最大值是;其中正确的结论是 .
三.解答题(共13小题)
25.我们常常把一张A4纸通过折叠的方式得到它的对角线,如图1.折纸活动中,通过点与点重合或边与边重合,才能得到精准的折叠.现有一张A4纸张(矩形ABCD),如图2,设折叠后B'C边与AD边重叠的点为E.
(1)请用尺规作图的方式在图2中画出点E.
(2)根据以上折纸活动的提示,描述折出A4纸(矩形ABCD)对角线的两个步骤.
26.在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
27.定义:有一组邻边垂直且对角线相等的四边形为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 .
(2)如图1,在3×3方格纸中,A,B,C在格点上,请画出两个符合条件的不全等的垂等四边形,使AC,BD是对角线,点D在格点上.
(3)如图2,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,AE=AF=CG且∠DGC=∠DEG,求证:四边形DEFG是垂等四边形.
28.计算题:
(1);
(2).
29.已知关于x的一元二次方程x2﹣(2m+1)x+m﹣2=0.
(1)求证:不论m取何值,方程总有两个不相等的实数根;
(2)若方程有两个实数根为x1,x2,且x1+x2+3x1x2=1,求m的值.
30.2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,该意见对学生睡眠时间提出了新的要求.为了了解某校初二年级学生的睡眠时长,随机抽取了初二年级男生和女生各20位,对其同一天的睡眠时长进行调查,并对数据进行收集、整理、描述和分析.下面给出了相关信息.
a.睡眠时长(单位:小时):
男生 7.7 9.9 9.8 5.5 9.6 9.6 8.6 9.8 9.9 7.9
9.0 7.5 7.7 8.5 9.2 8.7 9.2 9.3 9.2 9.4
女生 9.0 7.6 9.1 9.0 8.0 7.9 8.6 9.2 9.0 9.3
8.2 9.2 8.8 8.5 9.1 8.6 9.0 9.5 9.3 9.1
b.睡眠时长频数分布直方图(分组:5≤x<6,6≤x<7,7≤x<8,8≤x<9,9≤x<10):
c.睡眠时长的平均数、众数、中位数如下:
年级 平均数 众数 中位数
男生 8.8 m 9.2
女生 8.8 9.0 n
根据以上信息,回答下列问题:
(1)补全男生睡眠时长频数分布直方图;
(2)直接写出表中m,n的值;
(3)根据抽样调查情况,可以推断 (填“男生”或“女生”)睡眠情况比较好,理由为 .
31.阅读与思考
下面是小宇学习了“反比例函数的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)满足I的反比例函数关系,它的图象如图所示. 问题一:请写出这个反比例函数的表达式: .
问题二:如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?
方法 分析问题 解答过程
解法一 因为I中电流I≤10,可以得到关于R的不等式并求解 解:∵I= ,且I≤10, ∴ ≤10, ∵R>0, ∴10R≥※,(依据:★) ∴▲.
解法二 因为I,可以求出当电流I=10时相应的R值,并通过反比例函数的增减性求R的取值范围
任务:
(1)问题一中反比例函数的表达式为 ;
(2)问题二中※表示: ,★表示: ,▲表示: ;
(3)完成问题二中解法二的解答过程.
32.如图,点P在正方形ABCD的对角线BD延长线上,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F.
(1)若∠PAD=15°,
①求∠PEF的度数;
②设AB=4,求PE的长;
(2)求证:CEPD.
33.某研究性学习小组通过调查发现,在一节40分钟的课中,学生的注意力会随时间的变化而变化.开始上课时,学生的注意力逐渐集中,中间一段时间保持较为理想的稳定状态,随后开始分散.经试验分析可知,学生的注意力指数y随时间x(分)的变化规律如图所示,其中线段AB的函数表达式为:,线段BC持续的时间恰为10分钟,曲线CD为反比例函数图象的一部分.
(1)求m的值及曲线CD的函数表达式.
(2)若一道数学难题,需要讲解18分钟,为了效果较好,要求学生注意力指数y不低于32,那么老师能否在学生注意力全程达到要求的状态下讲解完这道题?请说明理由.
34.小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛.经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量y(毫克/立方米)与时间x(月)成正比例.施工结束后,y与x成反比例.这两个变量之间的关系如图所示.请根据图中信息,回答下列问题:
(1)施工过程中y关于x的函数解析式是 ;
(2)已知国际上适宜居住的甲醛含量标准为小于或等于0.08毫克/立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以入住?
(3)施工开始后的第2个月底到第4个月底,室内的甲醛含量一直在下降,假设这两个月每个月甲醛含量降低的百分率相同,求这个降低的百分率.(,结果精确到1%)
35.综合与实践
如图1,某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为a m.
【问题提出】
小组同学提出这样一个问题:若a=10,能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设AB为x m,BC为y m.由矩形地块面积为8m2,得到xy=8,满足条件的(x,y)可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为10m,得到2x+y=10,满足条件的(x,y)可看成一次函数y=﹣2x+10的图象在第一象限内点的坐标,同时满足这两个条件的(x,y)就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线l1:y=﹣2x+10的交点坐标为(1,8)和 ,因此,木栏总长为10m时,能围出矩形地块,分别为:AB=1m,BC=8m;或AB= m,BC= m.
(1)根据小颖的分析思路,完成上面的填空.
【类比探究】
(2)若a=6,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
【问题延伸】
当木栏总长为a m时,小颖建立了一次函数y=﹣2x+a.发现直线y=﹣2x+a可以看成是直线y=﹣2x通过平移得到的,在平移过程中,当过点(2,4)时,直线y=﹣2x+a与反比例函数的图象有唯一交点.
(3)请在图2中画出直线y=﹣2x+a过点(2,4)时的图象,并求出a的值.
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=﹣2x+a与图象在第一象限内交点的存在问题”.
(4)若要围出满足条件的矩形地块,且AB和BC的长均不小于1m,请直接写出a的取值范围.
36.已知反比例函数.
(1)若反比例函数的图象经过点(1,3),求k1的值.
(2)若点A(a﹣b,2),B(c﹣b,4)在函数的图象上,比较a,b,c的大小.
(3)反比例函数,如果m≤x≤m+1,且0<m<24,函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,试证明.
37.【方法初探】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.
问题:如图1,在△ABC中,AD⊥BC于点D,若CD=DB+AB,求证:∠B=2∠C.
解题思路:我们可以采用“截长补短法”解决该问题,如图2,辅助线做法在CD上截取DE=DB,连接AE,从而证明出结论.
请你根据上述解题思路,写出证明过程.
【方法应用】如图3,已知:等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD.
【实际应用】如图4,在四边形ABCD中,已知∠BAD=50°,∠D=110°,∠ACD=45°,∠BCA=85°,CE是△ABC的高,AD=12,EB=3,直接写出AE的长 .
一.选择题(共16小题)
1.使得式子有意义的x的取值范围是( )
A.x≥4 B.x>4 C.x≤4 D.x<4
【分析】直接利用二次根式有意义的条件分析得出答案.
【解答】解:使得式子有意义,则:4﹣x>0,
解得:x<4,
即x的取值范围是:x<4.
故选:D.
2.数学世界奇妙无穷,其中曲线是微分几何的研究对象之一,下列数学曲线既是轴对称图形,又是中心对称图形的是( )
A. B.
C. D.
【分析】根据轴对称图形与中心对称图形的概念求解.轴对称图形的关键是寻找对称轴,图形两部分折叠后可重合,中心对称图形是要寻找对称中心,图形旋转180°后与原图重合.
【解答】解:A.是轴对称图形,不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.既是中心对称图形,也是轴对称图形,符合题意;
D.是轴对称图形,不是中心对称图形,故此选项不合题意.
故选:C.
3.若2<a<3,则( )
A.5﹣2a B.1﹣2a C.2a﹣1 D.2a﹣5
【分析】根据二次根式的性质解答即可.
【解答】解:因为2<a<3,
所以a﹣2﹣(3﹣a)=a﹣2﹣3+a=2a﹣5,
故选:D.
4.在一次科技作品制作比赛中,某小组八件作品的成绩(单位:分)分别是7,10,9,8,7,9,9,8,对这组数据,下列说法正确的是( )
A.中位数是8 B.众数是9 C.平均数是8 D.方差是0
【分析】根据中位数、众数、平均数及方差的计算方法分别求解即可得到答案.
【解答】解:A、按照从小到大的顺序排列为7,7,8,8,9,9,9,10,由中位数的求解方法得到这组数据的中位数为,该选项错误,不符合题意;
B、这组数据中众数为9,该选项正确,符合题意;
C、这组数据平均数为,该选项错误,不符合题意;
D、这组数据的平均数为8.375,则方差为,该选项错误,不符合题意;
故选:B.
5.如图,在菱形ABCD中,E是对角线AC的中点,EF∥CB,交AB于点F,如果EF=3.5,那么菱形ABCD的周长为( )
A.28 B.14 C.7 D.3.5
【分析】根据中位线可得BC长为EF长的2倍,那么菱形ABCD的周长=4BC,问题得解.
【解答】解:∵E是AC的中点,
∴AE=CE,
∵EF∥CB,
∴,
∴AF=BF,
∴EF是△ABC的中位线,
∴BC=2EF=2×3.5=7,
∴菱形ABCD的周长是4×7=28,
故选:A.
6.反比例函数的图象上有A(a,y1),B(2a,y2),C(3a,y3)三点( )
A.若y1<0,则y1﹣y2>y2﹣y3
B.若y1>0,则y1﹣y2>y2﹣y3
C.若y1>0,则|y1﹣y2|<|y2﹣y3|
D.若y1<0,则|y1﹣y2|<|y2﹣y3|
【分析】根据反比例函数图象上点的坐标特征解答即可.
【解答】解:分别将点A(a,y1),B(2a,y2),C(3a,y3)代入解析式得:
y1,y2,y3,
∴y1﹣y2,y2﹣y3,
若y1<0,则0,
∴y1﹣y2<y2﹣y3<0,
∴|y1﹣y2|>|y2﹣y3|,
∴A,D均错误;
若y1>0,则0,
∴y1﹣y2>y2﹣y3>0,
∴|y1﹣y2|>|y2﹣y3|,
∴B正确,C错误.
故选:B.
7.若关于x的一元二次方程kx2﹣6x+9=0有实数根,则k的取值范围是( )
A.k<1 B.k≤1 C.k<1且k≠0 D.k≤1且k≠0
【分析】根据一元二次方程的定义及根的判别式即可判断.
【解答】解:∵一元二次方程kx2﹣6x+9=0有实数根,
∴(﹣6)2﹣4×9k≥0,且k≠0,
解得k≤1且k≠0,
故选:D.
8.如图所示,E是菱形ABCD对角线AC上的一点,若BC=6,DE=4,设AE=x,CE=y,则下列代数式为定值的是( )
A.y+x B.xy C.y﹣x D.y2+x2
【分析】连接BD,由菱形的性质推出BD⊥AC,OAAC(x+y),AD=BC=6,求出OE(y﹣x),由勾股定理得到42(y﹣x)2=62(x+y)2,得到xy=20.
【解答】解:连接BD,
∵四边形ABCD是菱形,
∴BD⊥AC,OAAC,AD=BC=6,
∵AE=x,CE=y,
∴AC=x+y,
∴OA(x+y),
∴OE=OA﹣AE(y﹣x),
∵OD2=DE2﹣OE2=AD2﹣AO2,
∴42(y﹣x)2=62(x+y)2,
∴xy=20.
∴代数式为定值的是xy.
故选:B.
9.如图,AC是正方形ABCD的对角线,点E是CD上一点,连结BE,分别过点A和C作BE的垂线,垂足分别为G和F,BE与AC交于点H,O是AC的中点,连结OF,OG,AB=5,有下列结论:①当AG=4时,FG=1;②OG平分∠AGE.关于这两个结论,下列说法正确的是( )
A.①②都对 B.①对,②错 C.①错,②对 D.①②都错
【分析】根据正方形的性质先证明△ABG≌△BCF(AAS),利用其性质结合勾股定理可判断①选项,延长FO交AG于N,证明△AON≌△COF(AAS),利用其性质可证明△FNG为等腰直角三角形,即可判断②.
【解答】解:∵四边形ABCD是正方形,点O是AC的中点,
∴AB=BC=CD=AD=5,∠ABC=∠BCD=∠ADC=∠DAB=90°,
∵AG⊥BE,CF⊥BE,
则AG∥CF,
∴∠AGB=∠BFC=90°,∠ABG+∠EBC=∠BCF+∠EBC=90°,
∴∠ABG=∠BCF,
∴△ABG≌△BCF(AAS),
∴AG=BF,
当AG=4时,,
则FG=BF﹣BG=AG﹣BG=1,故①选项正确;
延长FO交AG于N,
∵AG∥CF,
∴∠OAN=∠OCF,∠ONA=∠OFC,
∵点O为AC的中点,
∴OA=OC,
∴△AON≌△COF(AAS),
∴OF=ON,CF=AN,
∵NG=AG﹣AN,FG=BF﹣BG,
∴NG=FG,即:△FNG为等腰直角三角形,
∴OG平分∠AGE,故②正确.
故选:A.
10.在数学活动课上,老师和同学们判断一个四边形模具是否为菱形,下面是一个学习小组拟定的方案,其中正确的是( )
A.测量对角线是否互相平分且相等
B.测量对角线是否互相平分且垂直
C.测量三条边是否相等
D.测量对角线是否互相垂直且一组邻边相等
【分析】A.菱形的对角线性质是互相垂直且平分,而对角线互相平分且相等是矩形的判定条件.因为矩形的对角线具有互相平分且相等的特点,所以此条件不能判定四边形是菱形,A选项不符合要求.
B.根据平行四边形的判定定理,对角线互相平分的四边形是平行四边形.而菱形是特殊的平行四边形,在平行四边形的基础上,当对角线互相垂直时,就满足了菱形的判定条件,所以如果一个四边形对角线互相平分且垂直,可判定它是菱形,B选项符合要求.
C.菱形的定义是四条边都相等的四边形.仅三条边相等,无法确定第四条边的情况,不能依据此条件判定该四边形是菱形,C选项不符合要求.
D.菱形的判定需要满足特定的条件组合,“对角线互相垂直且一组邻边相等”这种条件组合,不满足菱形判定定理中的任何一条,不能判定该四边形是菱形,D选项不符合要求.
【解答】解:A.对角线互相平分且相等的四边形是矩形,不是菱形,所以该选项错误.
B.:对角线互相平分的四边形是平行四边形,在此基础上,若对角线还互相垂直,根据菱形的判定定理,这个平行四边形就是菱形,所以该选项正确.
C.仅测量三条边相等,不能判定这个四边形是菱形,菱形需要四条边都相等,所以该选项错误.
D.对角线互相垂直且一组邻边相等,不能判定这个四边形是菱形,不满足菱形的判定条件,所以该选项错误.
故选:B.
11.如图,矩形ABCO的两边分别在坐标轴上,OA=a,OC=b,点P在反比例函数(k为常数,k>0)的图象上,且在矩形ABCO内部,其横坐标为c.过点P作PE∥x轴交AC于点E,作PF∥y轴交AB于点F,连结EF,FC.记△EFC的面积为S,以下说法正确的是( )
A.S的值仅与a,b有关
B.S的值仅与c,k有关
C.S的值仅与k有关
D.S的值与a,b,c,k都有关
【分析】根据题意,先确定各点的坐标,C(b,0),B(b,a),A(0,a),P(c,),F(c,a),利用S△CEF=S△ABC﹣S△AEF﹣S△BCF得到结论即可.
【解答】解:如图,
由条件可知C(b,0),B(b,a),A(0,a),
∵点P在反比例函数(k为常数,k>0)的图象上,且横坐标为c,
∴P(c,),F(c,a),
∴S△AEF AF (a)(ac﹣k),
S△BCF,
S△ABC,
∴S△CEF=S△ABC﹣S△AEF﹣S△BCF,
∴△EFC的面积为S仅与k值有关.
故选:C.
12.折纸不仅具有艺术审美价值,还蕴含着许多数学知识.如图,一张长方形纸片ABCD,点E,F分别是线段AD,BC上的点,先将纸片沿EF折叠,点A,B的对应点分别为点A′,B',A'B'与线段AD交于点G,点H是线段DC上一点,再将纸片沿GH折叠,点D的对应点为点D',点B'恰好在GD'上,若测得∠BFE=66°,则∠DGH的度数是( )
A.21° B.26° C.33° D.42°
【分析】由矩形的性质得AD∥BC,∠A=90°,因为∠BFE=66°,所以∠DEF=∠BFE=66°,∠AEF=114°,由折叠得∠A′=∠A=90°,∠A′EF=∠AEF=114°,则∠A′EG=∠A′EF﹣∠DEF=48°,求得∠DGB′=∠EGA′=42°,而点B′在GD′上,所以∠DGD′=42°,则∠DGH∠DGD′=21°,于是得到问题的答案.
【解答】解:∵四边形ABCD是矩形,
∴AD∥BC,∠A=90°,
∵∠BFE=66°,
∴∠DEF=∠BFE=66°,∠AEF=180°﹣∠BFE=114°,
由折叠得∠A′=∠A=90°,∠A′EF=∠AEF=114°,∠DGH=∠D′GH,
∴∠A′EG=∠A′EF﹣∠DEF=114°﹣66°=48°,
∴∠DGB′=∠EGA′=90°﹣∠A′EG=42°,
∵点B′在GD′上,
∴∠DGD′=∠DGB′=42°,
∴∠DGH∠DGD′=21°,
故选:A.
13.如图,在△ABC中,∠C=90°,∠B=32°,E,F分别在边BC,AB上,将△BEF沿着EF折叠,得到△B'EF,B′E与AB交于G.当B′E∥AC时,∠AFB'的度数是( )
A.25° B.26° C.30° D.32°
【分析】由∠C=90°,∠B=32°,求得∠A=58°,由B′E∥AC,得∠AGB′=∠A=58°,由折叠得∠B′=∠B=32°,则58°=∠AFB′+32°,求得∠AFB′=26°,于是得到问题的答案.
【解答】解:∵∠C=90°,∠B=32°,
∴∠A=90°﹣∠B=58°,
∵B′E∥AC,
∴∠AGB′=∠A=58°,
∵将△BEF沿着EF折叠,得到△B'EF,
∴∠B′=∠B=32°,
∵∠AGB′=∠AFB′+∠B′,
∴58°=∠AFB′+32°,
∴∠AFB′=26°,
故选:B.
14.如图,是我国古代著名的赵爽弦图的示意图,其由四个全等的直角三角形拼接成一个正方形ABCD,连结AE,DE,若AD=AE,,则正方形ABCD的边长是( )
A. B. C. D.
【分析】由全等三角形的性质以及等腰三角形的性质可得△DEH是等腰直角三角形,根据勾股定理可得DH=HE=2,再由勾股定理,即可求解.
【解答】解:∵赵爽弦图的示意图由四个全等的直角三角形拼接成一个正方形ABCD,
∴BE=CH=DG,GH=EH=EF=FG,AF⊥BE,CH⊥DG,AB=AD=AE,
∴BF=EF=EC=EH=DH,
∴△DEH是等腰直角三角形,
由勾股定理得:,
∵,
∴HE=DH=2,
∴CH=4,
由勾股定理得:,
∴正方形ABCD的边长是,
故选:D.
15.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,射线EG与BC的延长线相交于点P.若∠P=30°,则的值是( )
A. B.3 C. D.
【分析】作CM⊥PG于点M,GN⊥PB于点N,设CM=x,在Rt△PCM中,求得CP=2x,,在Rt△CGM中,求得,,在Rt△PNG中,求得,,再证明∠GCN∽∠BCG,求得,据此求解即可.
【解答】解:作CM⊥PG于点M,GN⊥PB于点N,
设CM=x,
∴△PCM是直角三角形,
∵∠P=30°,
∴CP=2CM=2x,,
∵四边形EFGH是正方形,
∴∠FGC=∠FGH=90°,∠CGM=∠EGH=45°,
在Rt△CGM中,∠CGM=45°,
∴CM=GM=x,
∴,,
在Rt△PNG中,∠P=30°,
∴,,
∴,
∵∠GNC=∠BGC=90°,∠GCN=∠BCG,
∴∠GCN∽∠BCG,
∴,
∴,
∴,
∴,
故选:A.
16.“赵爽弦图”被人们称为“中国古代数学的图腾”,是数形结合的典型体现.如图,大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成.连接FH,DF,若,,则大正方形ABCD的边长为( )
A.5 B. C. D.
【分析】由全等三角形的性质可得EF=EH,先对Rt△EFH运用勾股定理求出EF,再对Rt△DEF运用勾股定理求出DE=AF,则AE即可求得,最后对Rt△AED运用勾股定理即可求解.
【解答】解:∵大正方形ABCD是由四个全等的直角三角形和小正方形EFGH组成,
∴AF=DE,DH=AE,∠AED=∠DEF=90°,
∴AF﹣AE=DE﹣DH,
∴EF=EH,
在直角三角形EFH中,,
由勾股定理得:EF2+EH2=HF2,
∴EF=EH=2,
在直角三角形DEF中,,
由勾股定理得:,
∴AE=AF﹣FE=5﹣2=3,
在直角三角形ADE中,由勾股定理得:,
故选:D.
二.填空题(共8小题)
17.如图,在 ABCD中,∠ABC=60°,AB=6,BC=10,点E是边BC上一点,将△ABE沿AE折叠后,点B的对应点为点F.
(1)如图1,连接DE,若点F恰好落在边DE上.则BE的长为 13 .
(2)如图2,连接BD,若EF∥BD,则BE的长为 4 .
【分析】(1)过点D作DH⊥BC,交BC的延长线于点H,利用轴对称的性质得到∠AEB=∠AED,利用平行四边形的性质,平行线的性质和等腰三角形的判定定理求出AD=DE=10,利用平行四边形的性质和含30°角的直角三角形的性质求得线段CH,DH,利用勾股定理求得EH,进而求得CE,则BE=BC﹣EC;
(2)延长EF交AD的延长线于点G,过点G作GH⊥BC于点H,过点D作DK⊥BC于点K,利用平行四边形的判定与性质得到BE=DG,设BE=DG=x,利用矩形的判定与性质得到HK=DG=x,GH=DK,再利用勾股定理和(1)的结论解答即可得出结论.
【解答】解:(1)过点D作DH⊥BC,交BC的延长线于点H,如图1,
∵四边形ABCD是平行四边形,
∴AD=BC=10,DC=AB=6,AD∥BC,DC∥AB,
∴∠DAE=∠AEB,∠DCH=∠ABC=60°,
由折叠得:△ABE≌△AFE,
∴∠AEB=∠AED,
∴∠AED=∠DAE,
∴AD=DE=10,
在Rt△DCH中,CHDC=3,DHDC=3,
在Rt△DEH中,EH,
∴CE=EH﹣CH3,
∴BE=BC﹣EC=10﹣(3)=13,
故答案为:13;
(2)延长EF交AD的延长线于点G,过点G作GH⊥BC于点H,过点D作DK⊥BC于点K,如图2,
∵BE∥AD,EF∥BD,
∴四边形BEGD为平行四边形,
∴BE=DG.
∴设BE=DG=x,则EC=10﹣x,
∵DK⊥BC,GH⊥BC,AD∥BC,
∴四边形DKHG为矩形,
∴HK=DG=x,GH=DK.
由(1)知:DK=3,CK=3,
∴EH=EC+CK+KH=10﹣x+3+x=13,
在Rt△EHG中,EG14,
由折叠得:∠AEB=∠AEG,
∵四边形ABCD是平行四边形,
∴AD∥BC,
∴∠DAE=∠AEB,
∴∠AEG=∠DAE,
∴EG=AG=14,
∴BE=DG=AG﹣AD=14﹣10=4,
故答案为:4.
18.计算6的结果是 4 .
【分析】先进行开方运算,再合并同类二次根式即可.
【解答】解:原式=264
=224
=4.
故答案为:4.
19.如图,用一条宽度相等的足够长的纸条打一个结(如图1),然后轻轻拉紧、压平就可以得到如图2所示的正五边形ABCDE.在图2中,∠ACD的度数为 72° .
【分析】先根据正五边形的性质得出正五边形内角的度数,再根据等腰三角形的性质求出∠BCA的度数,进而可得出结论.
【解答】解:∵五边形ABCDE是正五边形,
∴其每个内角为108°,且AB=BC,
∴△ABC是等腰三角形,
∴∠BCA=(180°﹣108°)÷2=36°,
∴∠ACD=∠BCE﹣∠BCA=108°﹣36°=72°.
故答案为:72°
20.对于字母m、n,定义新运算m☆n=mn﹣m﹣n,若方程x2+3x+1=0的解为a、b,则a☆b+2的值为 6. .
【分析】判断出a+b=﹣3,ab=1,再根据新定义计算即可.
【解答】解:∵方程x2+3x+1=0的解为a、b,
∴a+b=﹣3,ab=1,
∴a☆b+2=ab﹣a﹣b+2=1+3+2=6.
故答案为:6.
21.若α,β是一元二次方程x2﹣3x﹣8=0的两个根,则α2﹣4α﹣β的值为 5 .
【分析】将α2﹣4α﹣β化为α2﹣3α﹣(α+β)分别求出α2﹣3α=8、α+β=3即可求得答案.
【解答】解:∵α、β是一元二次方程x2﹣3x﹣8的两个根,
∴α2﹣3α﹣8=0,
∴α2﹣3α=8,
∵α+β=3,
∴α2﹣4α﹣β=α2﹣3α﹣α﹣β=α2﹣3α﹣(α+β)=8﹣3=5.
故答案为:5.
22.某社团统计成员一周的活动时间情况,列出了方差的计算公式:S2[2×(2)2+4×(3)2+3×(4)2+(8)2],则的值是 3.6 .
【分析】根据方差的计算公式得出这组数据为2、2、3、3、3、3、4、4、4、8,再根据平均数的定义列式计算即可.
【解答】解:由题意知,这组数据为2、2、3、3、3、3、4、4、4、8,
所以这组数据的平均数3.6,
故答案为:3.6.
23.已知点(﹣1,2)在反比例函数的图象上,当y≤2时,x的取值范围是 x≤﹣1或x>0 .
【分析】根据点(﹣1,2)在反比例函数的图象上,求出k的值,得到反比例函数解析式,再根据反比例函数的性质求解即可.
【解答】解:∵点(﹣1,2)在反比例函数的图象上,
∴k=﹣1×2=﹣2,
∴函数解析式为y,
∴图象位于二、四象限,
在每个象限内,y随x的增大而增大,
当y=2时,x=﹣1,
则当y≤2时,x≤﹣1或x>0.
故答案为:x≤﹣1或x>0.
24.如图,正方形ABCD的边长为1,点E在边AB上运动(不与点A,B重合),∠DAM=45°,点F在射线AM上,且,CF与AD相交于点G,连接EC、EF、EG.则下列结论:①∠ECF=45°;②FE平分∠AFG;③BE+DG=EG;④△EAF的面积的最大值是;其中正确的结论是 ①③ .
【分析】在BC上截取BH=BE,连接EH,如图:根据等腰直角三角形的性质得到EHBE,求得AF=EH,根据全等三角形的性质得到∠AEF=∠ECH,推出△ECF是等腰直角三角形,得到∠ECF=∠EFC=45°,故①正确;得到∠BEH=45°,求得∠AFE≠∠EFC,推出FE不平分∠AFG,故②错误,延长AD到H,使得DH=BE,根据全等三角形的性质得到∠ECB=∠DCH,EG=GH,得到EG=BE+DG,故③正确,设BE=x,则AE=1﹣x,AFx,根据三角形的面积公式和二次函数的性质即可得到结论.
【解答】解:在BC上截取BH=BE,连接EH,如图1:
∵BE=BH,∠EBH=90°,
∴EHBE,
∵AFBE,
∴AF=EH,
∵∠DAM=∠EHB=45°,∠BAD=90°,
∴∠FAE=∠EHC=135°,
∵BA=BC,BE=BH,
∴AE=HC,
∴△FAE≌△EHC(SAS),
∴∠AEF=∠ECH,
∵∠ECH+∠CEB=90°,
∴∠AEF+∠CEB=90°,
∴∠FEC=90°,
∴△ECF是等腰直角三角形,
∴∠ECF=∠EFC=45°,故①正确;
∵∠B=90°,
∴∠BEH=45°,
∵∠BEC<90°,
∴∠CEH<45°,
∴∠AFE<45°,
∴∠AFE≠∠EFC,
∴FE不平分∠AFG,故②错误,
延长AD到H,使得DH=BE,如图2:
可得△CBE≌△CDH(SAS),
∴∠ECB=∠DCH,
∴∠ECH=∠BCD=90°,
∴∠ECG=∠GCH=45°,
∵CG=CG,CE=CH,
∴△GCE≌△GCH(SAS),
∴EG=GH,
∵GH=DG+DH,DH=BE,
∴EG=BE+DG,故③正确,
设BE=x,则AE=1﹣x,AFx,
∴S△AEF (1﹣x)×xx2x(x2﹣x)(x)2,
∵0,
∴x时,△AEF的面积的最大值为.故④错误,
故答案为:①③.
三.解答题(共13小题)
25.我们常常把一张A4纸通过折叠的方式得到它的对角线,如图1.折纸活动中,通过点与点重合或边与边重合,才能得到精准的折叠.现有一张A4纸张(矩形ABCD),如图2,设折叠后B'C边与AD边重叠的点为E.
(1)请用尺规作图的方式在图2中画出点E.
(2)根据以上折纸活动的提示,描述折出A4纸(矩形ABCD)对角线的两个步骤.
【分析】(1)分别以A,C为圆心,AB,BC为半径作弧,两弧交于点B′,连接AB′,CB′,CB′交AD于点E;
(2)步骤一:点A,点C两点重合,得到折痕EE′;
步骤二:点E,点E′重合可以折出A4纸(矩形ABCD)对角线AC.
【解答】解:(1)如图2中,点E即为所求;
(2)如图3中,步骤一:点A,点C两点重合,得到折痕EE′;
步骤二:点E,点E′重合可以折出A4纸(矩形ABCD)对角线AC.
26.在矩形ABCD中,AB=4,BC=3,点P在线段BC上运动,作△ACD关于直线AP的对称△AC1D1(点C,D的对称点分别为C1,D1).
(1)如图1,当点C1在AB的延长线上时,求CC1的长.
(2)如图2,当点P与点C重合时,连结DD1,CD1、DD1交AB分别于点E、F.求证:BD1⊥DD1.
(3)当直线C1D1经过点B时,求CP的长.
【分析】(1)易得AC=5,所以AC1=AC=5,再利用勾股定理求解即可;
(2)连结BD交AC于点O,证OH为△BDD1的中位线,即可得证;
(3)连接PC1,证∠BC1P=90°,在Rt△AD1B中,BD1,所以BC1=4,再利用勾股定理建立方程求解即可.
【解答】(1)解:在矩形ABCD中,AB=4,BC=3,
∴,
∵△ACD、△ACD关于直线AP对称,
∴AC1=AC=5,
∴BC=AC﹣AB=1,
在Rt△BCC1中,由勾股定理得,
,
∴CC1的长为;
(2)证明:连结BD交AC于点O,
∵ABCD为矩形,
∴OB=OD
∵D,D1关于AC对称,
∴AC垂直平分DD1,
∴H为DD1的中点,
∴OH为△BDD1的中位线,
∴OH∥BD1,
∵AC⊥DD1,
∴∠DHO=90°,
∵OH∥BD,
∴∠BD1D=∠DHO=90°,
∴DD⊥BD1;
(3)解:连接PC1,
∵△ACD、△AC1D1关于直线AP对称,
∴AD=AD,CD=CD,∠ACD=∠AC1B∠ACP=∠AC1PPC=PC1,∠ADC=∠AC1C=90°,
∵∠ACD+∠ACP=90°
∴∠AC1B+∠AC1P=90°,
即∠BC1P=90°,
当直线C1D1经过点B时,
在Rt△AD1B中,BD1,
∴BC1=C1D1﹣BD1=4,
在Rt△BC1P中,,
∴,,
∴.
27.定义:有一组邻边垂直且对角线相等的四边形为垂等四边形.
(1)写出一个已学的特殊平行四边形中是垂等四边形的是 正方形或矩形 .
(2)如图1,在3×3方格纸中,A,B,C在格点上,请画出两个符合条件的不全等的垂等四边形,使AC,BD是对角线,点D在格点上.
(3)如图2,在正方形ABCD中,点E,F,G分别在AD,AB,BC上,AE=AF=CG且∠DGC=∠DEG,求证:四边形DEFG是垂等四边形.
【分析】(1)根据定义易得解;
(2)①画一个符合题意得矩形 ABCD,②根据BC=5,可以找点D使CD=5,并且满尊BD=AC即可得解;
(3)先证△ADF≌△CDG(SAS),可得DF=DG,再导角证DG=EG,进而得证.
【解答】(1)解:由题意可知:正方形,矩形,
故答案为:正方形或矩形;
(2)解:如图1中,四边形ABCD即为所求.
(3)证明:在正方形ABCD中,
∵AF=CG,AB=BC,
∴FB=BG,
∴∠AEF=∠AFE=45°,∠BFG=∠BGF=45°,
∴∠EFG=90°,
∵∠A=∠C=90°,DA=DC,AF=CG,
∴△ADF≌△CDG(SAS),
∴DF=DG,
∵AD∥CB,
∴∠EDG=∠DGC,
∵∠DGC=∠DEG,
∴∠GDE=∠GED,
∴DG=EG,
∴DF=EG,
∴四边形DEFG是垂等四边形.
28.计算题:
(1);
(2).
【分析】(1)根据负整数指数幂,零指数幂,绝对值,分母有理化等知识计算即可;
(2)根据根式的乘法法则计算即可.
【解答】解:(1)原式=﹣3﹣1+2
=﹣3﹣1+22
=﹣2;
(2)原式=24
=44
=122.
29.已知关于x的一元二次方程x2﹣(2m+1)x+m﹣2=0.
(1)求证:不论m取何值,方程总有两个不相等的实数根;
(2)若方程有两个实数根为x1,x2,且x1+x2+3x1x2=1,求m的值.
【分析】(1)根据根的判别式得出Δ=[﹣(2m+1)]2﹣4×1×(m﹣2)=4m2+9>0,据此可得答案;
(2)根据根与系数的关系得出x1+x2=2m+1,x1x2=m﹣2,代入x1+x2+3x1x2=1得出关于m的方程,解之可得答案.
【解答】(1)证明:∵Δ=[﹣(2m+1)]2﹣4×1×(m﹣2)
=4m2+4m+1﹣4m+8
=4m2+9>0,
∴无论m取何值,此方程总有两个不相等的实数根;
(2)解:由根与系数的关系,得x1+x2=2m+1,x1x2=m﹣2,
由x1+x2+3x1x2=1,得2m+1+3(m﹣2)=1,
解得m.
30.2021年7月24日中共中央办公厅、国务院办公厅颁布了《关于进一步减轻义务教育阶段学生作业负担和校外培训负担的意见》,该意见对学生睡眠时间提出了新的要求.为了了解某校初二年级学生的睡眠时长,随机抽取了初二年级男生和女生各20位,对其同一天的睡眠时长进行调查,并对数据进行收集、整理、描述和分析.下面给出了相关信息.
a.睡眠时长(单位:小时):
男生 7.7 9.9 9.8 5.5 9.6 9.6 8.6 9.8 9.9 7.9
9.0 7.5 7.7 8.5 9.2 8.7 9.2 9.3 9.2 9.4
女生 9.0 7.6 9.1 9.0 8.0 7.9 8.6 9.2 9.0 9.3
8.2 9.2 8.8 8.5 9.1 8.6 9.0 9.5 9.3 9.1
b.睡眠时长频数分布直方图(分组:5≤x<6,6≤x<7,7≤x<8,8≤x<9,9≤x<10):
c.睡眠时长的平均数、众数、中位数如下:
年级 平均数 众数 中位数
男生 8.8 m 9.2
女生 8.8 9.0 n
根据以上信息,回答下列问题:
(1)补全男生睡眠时长频数分布直方图;
(2)直接写出表中m,n的值;
(3)根据抽样调查情况,可以推断 男生 (填“男生”或“女生”)睡眠情况比较好,理由为 睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生 .
【分析】(1)求出男生8≤x<9的频数,然后即可将频数分布直方图补充完整;
(2)根据众数和中位数的定义即可得到m,n的值;
(3)根据统计量的意义判断,并说明理由即可.
【解答】解:(1)男生8≤x<9的频数为20﹣1﹣4﹣12=3,
补全男生睡眠时长频数分布直方图如下:
(2)∵男生睡眠时长中:9.2小时出现3次,是出现次数最多的数据,
∴m=9.2,
∵女生睡眠时长中位数是数据由小到大排列第10,第11个数据的平均数,由数据可知,第10,第11个数据分别为:9,9,
∴n=(9+9)÷2=9;
(3)根据题目中的信息可知,男生睡眠情况比较好,
理由为:睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生.
故答案为:男生,睡眠时长的平均数相等,男生睡眠时长的众数、中位数高于女生.
31.阅读与思考
下面是小宇学习了“反比例函数的应用”后所作的课堂学习笔记,请认真阅读并完成相应的任务.
已知蓄电池的电压为定值,使用蓄电池时,电流I(单位:A)与电阻R(单位:Ω)满足I的反比例函数关系,它的图象如图所示. 问题一:请写出这个反比例函数的表达式: I .
问题二:如果以此蓄电池为电源的用电器的限制电流不能超过10A,那么用电器可变电阻应控制在什么范围?
方法 分析问题 解答过程
解法一 因为I中电流I≤10,可以得到关于R的不等式并求解 解:∵I= ,且I≤10, ∴ ≤10, ∵R>0, ∴10R≥※,(依据:★) ∴▲.
解法二 因为I,可以求出当电流I=10时相应的R值,并通过反比例函数的增减性求R的取值范围
任务:
(1)问题一中反比例函数的表达式为 I ;
(2)问题二中※表示: 36 ,★表示: 不等式的两边同时乘(或除以)同一个正数,不等号的方向不变 ,▲表示: R≥3.6 ;
(3)完成问题二中解法二的解答过程.
【分析】(1)根据函数图象上点的坐标,利用反比例函数图象上点的坐标特征,即可求出U值,进而可得出反比例函数的表达式;
(2)由I,且I≤10,可得出10,结合R>0,即可求出R的取值范围;
(3)利用反比例函数图象上点的坐标特征,可求出当I=10时R的值,由36>0且R>0,利用反比例函数的性质,可得出I随R的增大而减小,再结合I≤10,即可求出R的取值范围.
【解答】解:(1)∵反比例函数I的图象过点(9,4),
∴4,
∴U=36,
∴反比例函数的表达式为I.
故答案为:I;
(2)∵I,且I≤10,
∴10,
∵R>0,
∴10R≥36(不等式的两边同时乘(或除以)同一个正数,不等号的方向不变),
∴R≥3.6.
故答案为:,,36,不等式的两边同时乘(或除以)同一个正数,不等号的方向不变,R≥3.6;
(3)解法二:当I=10时,10,
解得:R=3.6,
∵36>0,且R>0,
∴I随R的增大而减小,
又∵I≤10,
∴R≥3.6.
32.如图,点P在正方形ABCD的对角线BD延长线上,连接PA,过点P作PE⊥PA交BC的延长线于点E,过点E作EF⊥BP于点F.
(1)若∠PAD=15°,
①求∠PEF的度数;
②设AB=4,求PE的长;
(2)求证:CEPD.
【分析】(1)①根据正方形性质得∠ABP=∠ADB=∠CBP=45°,进而得∠APD=30°,再根据PE⊥PA,EF⊥BP得∠PEF=∠APD=30°;
②在FE上截取FG=FP,连接PG,BG,连接CG,则△PFG是等腰直角三角形,进而得∠FPG=45°,再证明△FBE是等腰直角三角形得BF=EF,∠FEB=45°,由此可判定△BFG和△EFP全等,则∠GBF=∠PEF=∠APD=30°,解得BG∥AP,再根据∠FPG=∠ABP=45°得AB∥PG,由此得四边形ABGP是平行四边形,则PG=AB=4,在Rt△PFG,由勾股定理得FPPG,然后在Rt△PEF中,根据∠PEF=30°即可得出PE的长;
(2)先证明四边形DCGP是平行四边形,则PD=CG,∠DCG=∠FPG=45°,进而得∠GCE=∠FEB=45°,则△GCE是等腰直角三角形,由勾股定理得CECG,由此即可得出结论.
【解答】(1)①解:∵四边形ABCD是正方形,点P在对角线BD的延长线上,
∴∠ABP=∠ADB=∠CBP=45°,
∵∠ADP是△ADP的外角,
∴∠ADP=∠PAD+∠APD,
∵∠PAD=15°,
∴45°=15°+∠APD,
∴∠APD=30°,
∵PE⊥PA,EF⊥BP,
∴∠APE=90°,∠PFE=90°,
∴∠APD+∠EPF=90°,∠PEF+∠EPF=90°,
∴∠PEF=∠APD=30°;
②解:在FE上截取FG=FP,连接PG,BG,连接CG,如图所示,
∵EF⊥BP,
∴∠BFG=∠EFP=90°,
∴△PFG是等腰直角三角形,
∴∠FPG=45°,
∵∠CBP=45°,EF⊥BP,
∴△FBE是等腰直角三角形,
∴BF=EF,∠FEB=45°,
在△BFG和△EFP中,
,
∴△BFG≌△EFP(SAS),
∴∠GBF=∠PEF=30°,
∴∠GBF=∠APD=30°,
∴BG∥AP,
又∵∠FPG=∠ABP=45°,
∴AB∥PG,
∴四边形ABGP是平行四边形,
∴PG=AB=4,
在等腰Rt△PFG中,
由勾股定理得:PGFP,
∴FPPG,
在Rt△PEF中,∠PEF=30°,
∴PE=2FP;
(2)证明:∵四边形ABCD是正方形,
∴AB=DC,AB∥DC,∠DCB=∠DCE=90°,
由(1)可知:四边形ABGP是平行四边形,
∴AB∥PG,AB=PG,
∴DC∥PG,DC=PG,
∴四边形DCGP是平行四边形,
∴PD=CG,∠DCG=∠FPG=45°,
∴∠GCE=∠DCE﹣∠DCG=45°,
∴∠GCE=∠FEB=45°,
∴△GCE是等腰直角三角形,
∴CG=EG,
由勾股定理得:CECG,
∵PD=CG,
∴CEPD.
33.某研究性学习小组通过调查发现,在一节40分钟的课中,学生的注意力会随时间的变化而变化.开始上课时,学生的注意力逐渐集中,中间一段时间保持较为理想的稳定状态,随后开始分散.经试验分析可知,学生的注意力指数y随时间x(分)的变化规律如图所示,其中线段AB的函数表达式为:,线段BC持续的时间恰为10分钟,曲线CD为反比例函数图象的一部分.
(1)求m的值及曲线CD的函数表达式.
(2)若一道数学难题,需要讲解18分钟,为了效果较好,要求学生注意力指数y不低于32,那么老师能否在学生注意力全程达到要求的状态下讲解完这道题?请说明理由.
【分析】(1)把y=40,x=m代入yx+15得40m+15,解方程得到m=10,求得B(10,40),得到C(20,40),设反比例函数的解析式为y,把C(20,40)代入y,解方程即可得到结论;
(2)分别求出注意力指数为32时的两个时间,再将两时间之差和18比较,大于18则能讲完,否则不能.
【解答】解:(1)把y=40,x=m代入yx+15得40m+15,
解得m=10,
∴B(10,40),
∵线段BC持续的时间恰为10分钟,
∴C(20,40),
设反比例函数的解析式为y,
把C(20,40)代入y得40得k=800,
∴曲线CD的函数表达式为y;
(2)令y=32,
∴32x+15,
∴x=6.8,
令y=32,
∴32,
∴x25,
∵25﹣6.8=18.2>18,
∴经过适当安排,老师能在学生注意力达到所需的状态下讲解完这道题目.
34.小明家在进行房屋装修时,使用了某品牌的装修材料,此材料会散发甲醛.经过测试,在自然扩散的情况下,从施工开始到结束,室内平均每立方米的甲醛含量y(毫克/立方米)与时间x(月)成正比例.施工结束后,y与x成反比例.这两个变量之间的关系如图所示.请根据图中信息,回答下列问题:
(1)施工过程中y关于x的函数解析式是 y=1.25x(0≤x≤0.8) ;
(2)已知国际上适宜居住的甲醛含量标准为小于或等于0.08毫克/立方米,按照这个标准,请问小明一家从施工开始计算,至少经过多久才可以入住?
(3)施工开始后的第2个月底到第4个月底,室内的甲醛含量一直在下降,假设这两个月每个月甲醛含量降低的百分率相同,求这个降低的百分率.(,结果精确到1%)
【分析】(1)施工过程中y与x成正比例函数,设出正比例函数解析式,把(0.8,1)代入即可求得相应的函数解析式;
(2)当x>0.8时,y与x成反比例函数解析式,设出反比例函数解析式,把(0.8,1)代入即可求得相应的函数解析式,进而取y=0.08,得到相应的x的值即为可以入住的时间;
(3)取x=2,x=4,得到相应的y的值,进而设降低的百分率为m,根据2月底的甲醛含量(1﹣降低的百分率)2=4月底的甲醛含量,计算后取得合适的解即可.
【解答】解:(1)当0≤x≤0.8时,设y=kx,
∵经过点(0.8,1),
∴0.8k=1,
解得:k=1.25,
∴y=1.25x;
∴施工过程中y关于x的函数解析式为:y=1.25x(0≤x≤0.8).
故答案为:y=1.25x(0≤x≤0.8);
(2)当x>0.8时,设y,
∵经过点(0.8,1),
∴a=0.8,
∴y,
当y=0.08时,x=10.
答:小明一家从施工开始计算,至少经过10个月才可以入住;
(3)当x=2时,y=0.4,
当x=4时,y=0.2.
设这两个月降低的百分率为m,
0.4(1﹣m)2=0.2,
(1﹣m)2,
解得:m1=1(不合题意,舍去),m2=10.293≈29.3%.
答:降低的百分率约为29.3%.
35.综合与实践
如图1,某兴趣小组计划开垦一个面积为8m2的矩形地块ABCD种植农作物,地块一边靠墙,另外三边用木栏围住,木栏总长为a m.
【问题提出】
小组同学提出这样一个问题:若a=10,能否围出矩形地块?
【问题探究】
小颖尝试从“函数图象”的角度解决这个问题:
设AB为x m,BC为y m.由矩形地块面积为8m2,得到xy=8,满足条件的(x,y)可看成是反比例函数的图象在第一象限内点的坐标;木栏总长为10m,得到2x+y=10,满足条件的(x,y)可看成一次函数y=﹣2x+10的图象在第一象限内点的坐标,同时满足这两个条件的(x,y)就可以看成两个函数图象交点的坐标.
如图2,反比例函数的图象与直线l1:y=﹣2x+10的交点坐标为(1,8)和 (4,2) ,因此,木栏总长为10m时,能围出矩形地块,分别为:AB=1m,BC=8m;或AB= 4 m,BC= 2 m.
(1)根据小颖的分析思路,完成上面的填空.
【类比探究】
(2)若a=6,能否围出矩形地块?请仿照小颖的方法,在图2中画出一次函数图象并说明理由.
【问题延伸】
当木栏总长为a m时,小颖建立了一次函数y=﹣2x+a.发现直线y=﹣2x+a可以看成是直线y=﹣2x通过平移得到的,在平移过程中,当过点(2,4)时,直线y=﹣2x+a与反比例函数的图象有唯一交点.
(3)请在图2中画出直线y=﹣2x+a过点(2,4)时的图象,并求出a的值.
【拓展应用】
小颖从以上探究中发现“能否围成矩形地块问题”可以转化为“y=﹣2x+a与图象在第一象限内交点的存在问题”.
(4)若要围出满足条件的矩形地块,且AB和BC的长均不小于1m,请直接写出a的取值范围.
【分析】(1)观察图象或联立解方程组得到另一个交点坐标为(4,2);
(2)观察图象得到l2 与函数 图象没有交点,所以不能围出;
(3)平移直线y=﹣2x通过(2,4),将点(2,4)代入y=﹣2x+a,解得a=8;
(4)AB和BC的长均不小于1m,所以1≤x≤8,直线y=﹣2x+a在l3、l4之间移动,可得求a的范围.
【解答】解:(1)将反比例函数y与直线l1:y=﹣2x+10联立得:
,
∴2x+10,
整理得:x2﹣5x+4=0,
解得:x1=1,x2=4,
∴另一个交点坐标为(4,2),
∵AB为x m,BC为y m,
∴AB=4,BC=2.
故答案为:(4,2);4;2;
(2)a=6,不能围出矩形地块;理由如下:
y=﹣2x+6的图象,如图中直线l2所示:
∵l2 与函数 图象没有交点,
∴不能围出面积为8m2的矩形;
(3)如图中直线l3所示:
将点(2,4)代入y=﹣2x+a得:4=﹣2×2+a,
解得a=8.
(4)∵AB和BC的长均不小于1m,
∴x≥1,y≥1,
∴1,
∴x≤8,
∴1≤x≤8,
如图所示,直线y=﹣2x+a在l4、l3之间移动,
把(8,1)代入y=﹣2x+a得a=17,
∴8≤a≤17.
36.已知反比例函数.
(1)若反比例函数的图象经过点(1,3),求k1的值.
(2)若点A(a﹣b,2),B(c﹣b,4)在函数的图象上,比较a,b,c的大小.
(3)反比例函数,如果m≤x≤m+1,且0<m<24,函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,试证明.
【分析】(1)将点(1,3)坐标代入求出k1即可;
(2)根据反比例函数图象上点的坐标特征及反比例函数性质解答即可;
(3)由反比例函数的性质可得y2的最大值为,最小值为,y1的最大值为,最小值为,由题意列出两个方程,即可求解.
【解答】(1)解:将点(1,3)坐标代入得:3,
解得:k1=3,
(2)解:∵中k1>0,
∴反比例函数图象分布在第一三象限,y随x的增大而减小,
∵2<4,
∴a﹣b>c﹣b,a﹣b>0,c﹣b>0,
∴a>c>b;
(3)证明:∵反比例函数,如果m≤x≤m+1,且0<m<24,
∴y2随x的增大而增大,则y2的最大值为,最小值为,
∵反比例函数.如果m≤x≤m+1,且0<m<24,
∴y1随x的增大而减小,则y1的最大值为,最小值为,
∵函数y1的最大值比函数y2的最大值大5,函数y1的最小值比函数y2的最小值大4.8,
∴5,4.8,
∴(m+1)k1﹣k2m=5m(m+1)①,mk1﹣(m+1)k2=4.8m(m+1)②,
∴①﹣②得:k1+k2=0.2m(m+1),
∴k1+k2.
37.【方法初探】截长补短法,是初中几何题中一种添加辅助线的方法,也是把几何题化难为易的一种策略.
问题:如图1,在△ABC中,AD⊥BC于点D,若CD=DB+AB,求证:∠B=2∠C.
解题思路:我们可以采用“截长补短法”解决该问题,如图2,辅助线做法在CD上截取DE=DB,连接AE,从而证明出结论.
请你根据上述解题思路,写出证明过程.
【方法应用】如图3,已知:等腰直角三角形ABC中,∠B=90°,AD是角平分线,交BC边于点D.求证:AC=AB+BD.
【实际应用】如图4,在四边形ABCD中,已知∠BAD=50°,∠D=110°,∠ACD=45°,∠BCA=85°,CE是△ABC的高,AD=12,EB=3,直接写出AE的长 15 .
【分析】【方法初探】根据已知可得AD是BE的垂直平分线,从而可得AB=AE,进而可得∠B=∠AEB,然后结合已知AB+BD=DC,可得AB=EC,从而可得AE=EC,进而可得∠C=∠EAC,最后利用三角形的外角性质可得∠AEB=2∠C,即可解答;
【方法应用】先证明△ABD≌△AHD得到AH=AB,BD=HD,再证明△CDH是等腰直角三角形,推出BD=HC,据此根据线段的和差关系即可证明结论;
【实际应用】由三角形内角和定理可得∠DAC=25°,证明△DAC≌△FAC(SAS)得出∠AFC=∠D=110°,再证明△CEF≌△CEB(AAS)得出EF=BE,求出BF=2BE=6,即可得解.
【解答】【方法初探】证明:如图2,在DC上截取DE=DB,连接AE,
∵AD⊥BC,BD=DE,
∴AD是BE的垂直平分线,
∴AB=AE,
∴∠B=∠AEB,
∵AB+BD=DC,DE+EC=DC,
∴AB=EC,
∴AE=EC,
∴∠C=∠EAC,
∵∠AEB=∠C+∠EAC,
∴∠AEB=2∠C,
∴∠B=2∠C;
【方法应用】证明:如图所示,过点D作DH⊥AC于H,
∴∠AHD=90°=∠B,
∵AD是角平分线,
∴∠BAD=∠HAD,
又∵AD=AD,
∴△ABD≌△AHD(AAS),
∴AH=AB,BD=HD,
∵△ABC是等腰直角三角形,
∴∠C=45°,
∴△CDH是等腰直角三角形,
∴HD=HC,
∴BD=HC,
∵AC=AH+CH,
∴AC=AB+BD;
【实际应用】解:在AE上截取AF=AD,连接CF,
由题意可得:
∴∠DAC=180°﹣∠D﹣∠ACD=25°,
∴∠FAC=∠BAD﹣∠DAC=25°,
∴∠DAC=∠FAC=25°,
∵AC=AC,
在△DAC和△FAC中,
,
∴△DAC≌△FAC(SAS),
∴∠AFC=∠D=110°,
∴∠CFE=180°﹣∠AFC=70°,
∴∠B=180°﹣∠ACB﹣∠FAC=70°,
∴∠B=∠CFE,
∵CE⊥AB,
∴∠CEF=∠CEB=90°,
∴CE=CE,
在△CEF和△CEB中,
,
∴△CEF≌△CEB(AAS),
∴EF=BE,
∴BF=2BE=6,
∴AB=AF+BF=12+6=18,
∴AE=AB﹣BE=18﹣3=15.
故答案为:15.
同课章节目录
