第十七章 勾股定理 检测卷 (含答案)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第十七章 勾股定理 检测卷 (含答案)2024-2025学年人教版数学八年级下册 | 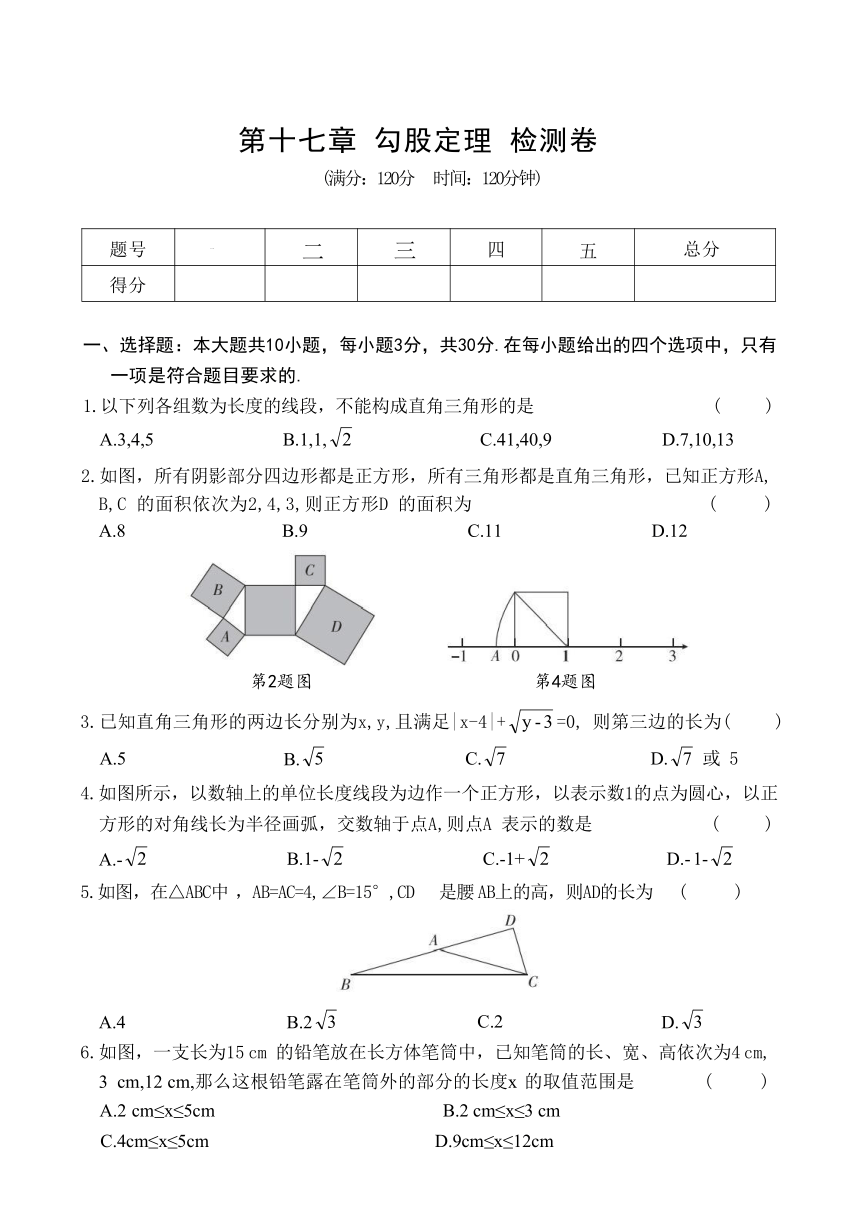 | |
| 格式 | docx | ||
| 文件大小 | 228.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:44:10 | ||
图片预览




文档简介
第十七章 勾股定理 检测卷
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.以下列各组数为长度的线段,不能构成直角三角形的是 ( ) A.3,4,5 B.1,1, C.41,40,9 D.7,10,13
2.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,已知正方形A, B,C 的面积依次为2,4,3,则正方形D 的面积为 ( ) A.8 B.9 C.11 D.12
第2题图 第4题图
3.已知直角三角形的两边长分别为x,y,且满足|x-4|+=0, 则第三边的长为( ) A.5 B. C. D. 或 5
4.如图所示,以数轴上的单位长度线段为边作一个正方形,以表示数1的点为圆心,以正 方形的对角线长为半径画弧,交数轴于点A,则点A 表示的数是 ( ) A.- B.1- C.-1+ D.- 1-
5.如图,在△ABC中 ,AB=AC=4,∠B=15°,CD 是腰 AB上的高,则AD的长为 ( )
A.4 B.2 C.2 D.
6.如图,一支长为15 cm 的铅笔放在长方体笔筒中,已知笔筒的长、宽、高依次为4 cm,
3 cm,12 cm,那么这根铅笔露在笔筒外的部分的长度x 的取值范围是 ( )
A.2 cm≤x≤5cm B.2 cm≤x≤3 cm
C.4cm≤x≤5cm D.9cm≤x≤12cm
第6题图
第7题图
第8题图
7.临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城 和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6 m 且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到 达柱顶正上方(从点A 到点C,B 为AC 的中点),每根华表刻有雕龙的部分的柱身高约 16m, 则雕刻在石柱上的巨龙至少为 ( ) A.20m B.25m C.30m D.15m
8.如图,在四边形ABCD 中,对角线分别为AC,BD, 且 AC⊥BD 交于点0,若AD=2,BC=
6,则AB2+CD2 的值为 ( ) A.40 B.38 C.36 D.32
9.如图,在3×3的正方形网格中,若小正方形的边长是1,则任意两个格点间的距离不可 能是 ( ) A.2 B.2 C. D.
第9题图
第10题图
第11题图
10.如图,钓鱼竿AB的长为6m, 露在水面上的鱼线BC 长为2m. 钓鱼者想看鱼钩上的情 况,把钓鱼竿AB转到AB′的位置,此时露在水面上的鱼线B'C′ 长为3 m, 则 CC′的 长为 ( )
A. m B.2 m C.m D.2m
二、填空题:本大题共5小题,每小题3分,共15分.
11. 如图,在 Rt△ABC中,∠C=90°,∠A=45°,AB=10, 则 AC的长为
12.一座垂直于两岸的桥长27 m,一艘小船自桥北头出发,向正南方向驶去,因水流原因, 到达南岸后,发现已偏离桥南头36m, 则小船实际行驶了 m.
13.如图,有一张直角三角形纸片,两直角边 AC=4cm,BC=8cm, 将△ABC 折叠,使点B与点A 重合,折痕为DE, 则 CD 的长是 .
第13题图
第14题图
第15题图
14. 如 图 ,Rt△ABC 中,分别以这个三角形的三边为边长作正方形,面积分别记为S ,S , S . 如 果S +S -S =24, 则阴影部分的面积为
15. 如图,正方形网格中,每一小格的边长为1.网格内有△PAB,则∠PAB+∠PBA 的度数 是
三、解答题(一):本大题共3小题,每小题7分,共21分.
16. 在 Rt△ABC 中,∠C=90° .
(1)若AB=15,AC=12, 求 BC的长;
(2)若AB=6,∠A=30°, 求 BC 的长 .
17.如图,正方形网格中每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为 顶点按下列要求画三角形.
(1)在图①中画三角形,使三角形为等腰三角形且底边长为2,腰长为 ;
(2)在图②中画三角形,使三角形为直角三角形且一条直角边长为 ,斜边长为5.
图① 图②
18.某游乐场部分平面图如图所示,点D,C,A 在同一直线上,点A,B 在同一直线上,DA⊥ AB,测得AC=60m,AB=80m,DC=75m.
(1)求入口B 到大摆锤 C 的距离.
(2)现要在距离大摆锤45 m 的 E 处修建游乐项目旋转木马,点B,C,E 在同一直线 上,此时旋转木马E 到过山车 D的距离最近.
①DE与 EC 的位置关系为 ;
②求过山车D 到旋转木马E 的距离.
A(出口) B(入口)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,笔直的公路上A,B 两点相距17km,C,D为两村庄,DA⊥AB 于点A,CB⊥AB于点 B, 已知DA=12 km,CB=5km,现在要在公路的AB 段上建一个公交车站E, 使得 C,D 两村到公交车站E的距离相等.则公交车站E 应建在离点A 多远处
20. 如图,在四边形ABCD中 ,AB=20,BC=15,CD=7,AD=24,∠B=90° .
(1)求证:CD⊥AD;
(2)求四边形ABCD的面积.
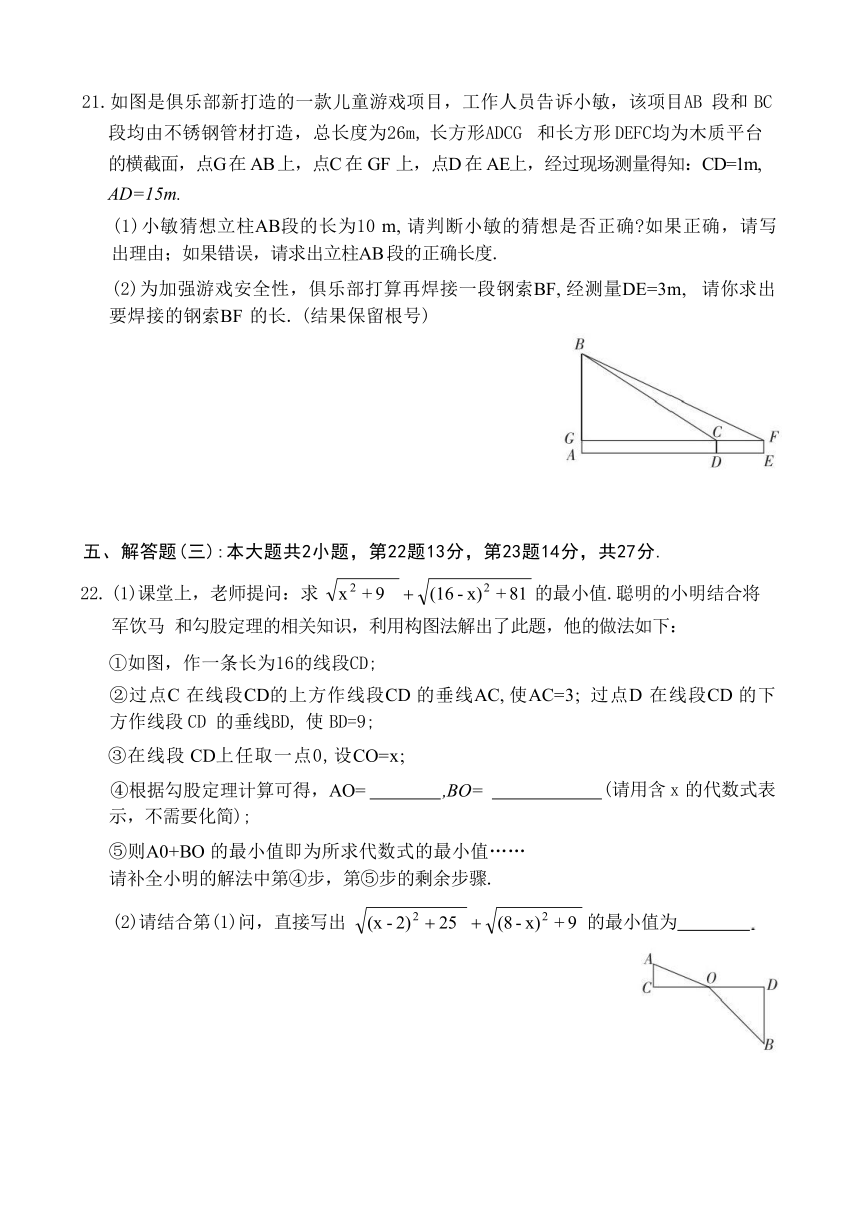
21.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB 段和 BC 段均由不锈钢管材打造,总长度为26m, 长方形ADCG 和长方形 DEFC均为木质平台 的横截面,点G 在 AB 上,点C 在 GF 上,点D 在 AE上,经过现场测量得知:CD=1m, AD=15m.
(1)小敏猜想立柱AB段的长为10 m, 请判断小敏的猜想是否正确 如果正确,请写 出理由;如果错误,请求出立柱AB 段的正确长度.
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF, 经测量DE=3m, 请你求出 要焊接的钢索BF 的长. (结果保留根号)
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22. (1)课堂上,老师提问:求 的最小值.聪明的小明结合将军饮马 和勾股定理的相关知识,利用构图法解出了此题,他的做法如下:
①如图,作一条长为16的线段CD;
②过点C 在线段CD的上方作线段CD 的垂线AC, 使AC=3; 过点D 在线段CD 的下 方作线段 CD 的垂线BD, 使 BD=9;
③在线段 CD上任取一点0,设CO=x;
④根据勾股定理计算可得,AO= ,BO= (请用含 x 的代数式表 示,不需要化简);
⑤则A0+BO 的最小值即为所求代数式的最小值…… 请补全小明的解法中第④步,第⑤步的剩余步骤.
(2)请结合第(1)问,直接写出 的最小值为
23. 如图,已知△ABC 中,∠B=90°,AB=16cm,BC=12 cm,P,Q是△ABC 边上的两个动
点,其中点P 从点A 开始沿A→B方向运动,且速度为每秒1 cm,点 Q 从点B 开始沿
B→C→A 方向运动,且速度为每秒2 cm, 它们同时出发,设运动的时间为t s.
备用图
(1)运动2 s 后,求PQ 的长.
(2)当点Q 在边BC上运动时,运动几秒后,△PQB是等腰三角形
(3)当点Q 在边CA 上运动时,求能使△BCQ是等腰三角形的运动时间.
第十七章检测卷
1.D 2.B 3.D 4.B 5.B 6.B 7.A 8.A 9.D 10.A 11.5√2 12.45 13.3cm 14.6 15.45°
16. 解:(1)∵∠C=90°,AB=15,AC=12, ∴BC===9.
(2) ∵∠C=90°,AB=6, ∠A=30°,
17. 解:(1)如图①,△ABC 即为所求.
(2)如图②,△ABC 即为所求.
图②
18. 解:(1)∵DA⊥AB,AC=60m,AB=80m, ∴BC===100(m).
答:入口B 到大摆锤 C 的距离为100m.
(2)①DE⊥EC
②∵∠DEC=90°,CD=75m,CE=45m, ∴DE===60(m).
答:过山车D 到旋转木马E 的距离为60 m.
19.解:∵C,D 两村到公交车站 E 的距离相等, ∴DE=EC.
∵DA⊥AB,CB⊥AB,
∴∠A=∠B=90°.
∴AE +AD =DE ,BE +BC =EC .
∴AE +AD =BE +BC .
设 AE=x km,则 BE=AB-AE=(17-x)km.
∵DA=12 km,CB=5 km,
∴x +12 =(17-x) +5 .
解得x=5.∴AE=5km.
答:公交车站E 应建在离点A 5km处 .
20. (1)证明:如图,连接AC.
∵∠B=90°,
∴AC =AB +BC =20 +15 =625 . ∵AD +CD =24 +7 =625,
∴AC =AD +CD .
∴△ADC 是直角三角形,∠D=90°.
∴CD⊥AD.
(2)解:S四边形ABCD=S△ABc+S△ADC
=234
21.解:(1)不正确.
由题意,得AG=CD=1m,GC=AD=15m,∠AGC=∠BGC=90° . 设BG=xm, 则BC=(26-1-x)m.
在 Rt△BGC中,由勾股定理,得BG +CG =CB , 即 x +15 =(26-1-x) .
解得x=8.∴BG=8m.
∴AB=BG+GA=9(m).
∴立柱AB 段的正确长度为9m.
(2)由题意,得 CF=DE=3m, ∴GF=GC+CF=18(m).
在 Rt△BGF 中,由勾股定理,得 BF== =(m).
∴钢索BF 的长为m.
22. 解:(1)④
⑤如图,连接AB, 交 CD于点O', 则此时A0+BO 取得最 小值,延长AC 到点A′, 连接A'B, 使四边形A'CDB 是长 方形,则∠A'=90°,A'C=BD=9.
∴AB===20.
∴A0+BO 的最小值,即代数式 ++81 的最小值为20.
(2)10 [提示]如图,作线段ED=8,C 为线段ED 上一点,且CE=2. 过点C 在线段 CD的上方作线段CD的垂线 AC, 使AC=5; 过点D 在线段CD的下方作线段CD的 垂线BD, 使 BD=3. 连接AB,交 CD于点0,如图所示.
设 OE=x, 则CO=x-2,DO=8-x.
23. 解:(1)当t=2 时 ,AP=2cm,BQ=2t=4cm ∵AB=16cm, ∴BP=AB-AP=16-2=14(cm). ∴PQ===(cm).
(2)由题意,可知AP=t cm,BQ=2t cm. ∵AB=16cm, ∴BP=AB-AP=(16-t)cm.
当△PQB 为等腰三角形时,BP=BQ, 即16-t=2t.
解得
∴运云后,△ PQB 是等腰三角形.
(3)①当CQ=BQ 时,如图所示,则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,∠A+∠C=90°. ∴∠A=∠ABQ. ∴BQ=AQ. CQ=AQ ∵AC===20(cm), ∴CQ=AQ=10 cm. ∴BC+CQ=22 cm. ∴t=22÷2=11.
②当CQ=BC 时,如图所示.
此时BC+CQ=24 cm. ∴t=24÷2=12.
③ 当BC=BQ 时,如图所示,过点B 作 BE⊥AC于点E
则(cm)
∴
∴CQ=2CE=14.4cm.∴BC+CQ=26.4 cm.
∴t=26.4÷2=13.2.
综上所述,当运动时间为11s 或 12s 或13.2s 时 ,△BCQ 是等腰三角形.
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.以下列各组数为长度的线段,不能构成直角三角形的是 ( ) A.3,4,5 B.1,1, C.41,40,9 D.7,10,13
2.如图,所有阴影部分四边形都是正方形,所有三角形都是直角三角形,已知正方形A, B,C 的面积依次为2,4,3,则正方形D 的面积为 ( ) A.8 B.9 C.11 D.12
第2题图 第4题图
3.已知直角三角形的两边长分别为x,y,且满足|x-4|+=0, 则第三边的长为( ) A.5 B. C. D. 或 5
4.如图所示,以数轴上的单位长度线段为边作一个正方形,以表示数1的点为圆心,以正 方形的对角线长为半径画弧,交数轴于点A,则点A 表示的数是 ( ) A.- B.1- C.-1+ D.- 1-
5.如图,在△ABC中 ,AB=AC=4,∠B=15°,CD 是腰 AB上的高,则AD的长为 ( )
A.4 B.2 C.2 D.
6.如图,一支长为15 cm 的铅笔放在长方体笔筒中,已知笔筒的长、宽、高依次为4 cm,
3 cm,12 cm,那么这根铅笔露在笔筒外的部分的长度x 的取值范围是 ( )
A.2 cm≤x≤5cm B.2 cm≤x≤3 cm
C.4cm≤x≤5cm D.9cm≤x≤12cm
第6题图
第7题图
第8题图
7.临汾是帝尧之都,有着尧都之称.尧都华表柱身祥云腾龙,顶蹲冲天吼,底座浮雕长城 和黄河壶口瀑布,是中华民族历史悠久、文化灿烂的标志.如图,在底面周长约为6 m 且带有层层回环不断的云朵石柱上,有一条雕龙从柱底沿立柱表面均匀地盘绕2圈到 达柱顶正上方(从点A 到点C,B 为AC 的中点),每根华表刻有雕龙的部分的柱身高约 16m, 则雕刻在石柱上的巨龙至少为 ( ) A.20m B.25m C.30m D.15m
8.如图,在四边形ABCD 中,对角线分别为AC,BD, 且 AC⊥BD 交于点0,若AD=2,BC=
6,则AB2+CD2 的值为 ( ) A.40 B.38 C.36 D.32
9.如图,在3×3的正方形网格中,若小正方形的边长是1,则任意两个格点间的距离不可 能是 ( ) A.2 B.2 C. D.
第9题图
第10题图
第11题图
10.如图,钓鱼竿AB的长为6m, 露在水面上的鱼线BC 长为2m. 钓鱼者想看鱼钩上的情 况,把钓鱼竿AB转到AB′的位置,此时露在水面上的鱼线B'C′ 长为3 m, 则 CC′的 长为 ( )
A. m B.2 m C.m D.2m
二、填空题:本大题共5小题,每小题3分,共15分.
11. 如图,在 Rt△ABC中,∠C=90°,∠A=45°,AB=10, 则 AC的长为
12.一座垂直于两岸的桥长27 m,一艘小船自桥北头出发,向正南方向驶去,因水流原因, 到达南岸后,发现已偏离桥南头36m, 则小船实际行驶了 m.
13.如图,有一张直角三角形纸片,两直角边 AC=4cm,BC=8cm, 将△ABC 折叠,使点B与点A 重合,折痕为DE, 则 CD 的长是 .
第13题图
第14题图
第15题图
14. 如 图 ,Rt△ABC 中,分别以这个三角形的三边为边长作正方形,面积分别记为S ,S , S . 如 果S +S -S =24, 则阴影部分的面积为
15. 如图,正方形网格中,每一小格的边长为1.网格内有△PAB,则∠PAB+∠PBA 的度数 是
三、解答题(一):本大题共3小题,每小题7分,共21分.
16. 在 Rt△ABC 中,∠C=90° .
(1)若AB=15,AC=12, 求 BC的长;
(2)若AB=6,∠A=30°, 求 BC 的长 .
17.如图,正方形网格中每个小正方形的边长都是1,每个小格的顶点叫做格点,以格点为 顶点按下列要求画三角形.
(1)在图①中画三角形,使三角形为等腰三角形且底边长为2,腰长为 ;
(2)在图②中画三角形,使三角形为直角三角形且一条直角边长为 ,斜边长为5.
图① 图②
18.某游乐场部分平面图如图所示,点D,C,A 在同一直线上,点A,B 在同一直线上,DA⊥ AB,测得AC=60m,AB=80m,DC=75m.
(1)求入口B 到大摆锤 C 的距离.
(2)现要在距离大摆锤45 m 的 E 处修建游乐项目旋转木马,点B,C,E 在同一直线 上,此时旋转木马E 到过山车 D的距离最近.
①DE与 EC 的位置关系为 ;
②求过山车D 到旋转木马E 的距离.
A(出口) B(入口)
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,笔直的公路上A,B 两点相距17km,C,D为两村庄,DA⊥AB 于点A,CB⊥AB于点 B, 已知DA=12 km,CB=5km,现在要在公路的AB 段上建一个公交车站E, 使得 C,D 两村到公交车站E的距离相等.则公交车站E 应建在离点A 多远处
20. 如图,在四边形ABCD中 ,AB=20,BC=15,CD=7,AD=24,∠B=90° .
(1)求证:CD⊥AD;
(2)求四边形ABCD的面积.
21.如图是俱乐部新打造的一款儿童游戏项目,工作人员告诉小敏,该项目AB 段和 BC 段均由不锈钢管材打造,总长度为26m, 长方形ADCG 和长方形 DEFC均为木质平台 的横截面,点G 在 AB 上,点C 在 GF 上,点D 在 AE上,经过现场测量得知:CD=1m, AD=15m.
(1)小敏猜想立柱AB段的长为10 m, 请判断小敏的猜想是否正确 如果正确,请写 出理由;如果错误,请求出立柱AB 段的正确长度.
(2)为加强游戏安全性,俱乐部打算再焊接一段钢索BF, 经测量DE=3m, 请你求出 要焊接的钢索BF 的长. (结果保留根号)
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22. (1)课堂上,老师提问:求 的最小值.聪明的小明结合将军饮马 和勾股定理的相关知识,利用构图法解出了此题,他的做法如下:
①如图,作一条长为16的线段CD;
②过点C 在线段CD的上方作线段CD 的垂线AC, 使AC=3; 过点D 在线段CD 的下 方作线段 CD 的垂线BD, 使 BD=9;
③在线段 CD上任取一点0,设CO=x;
④根据勾股定理计算可得,AO= ,BO= (请用含 x 的代数式表 示,不需要化简);
⑤则A0+BO 的最小值即为所求代数式的最小值…… 请补全小明的解法中第④步,第⑤步的剩余步骤.
(2)请结合第(1)问,直接写出 的最小值为
23. 如图,已知△ABC 中,∠B=90°,AB=16cm,BC=12 cm,P,Q是△ABC 边上的两个动
点,其中点P 从点A 开始沿A→B方向运动,且速度为每秒1 cm,点 Q 从点B 开始沿
B→C→A 方向运动,且速度为每秒2 cm, 它们同时出发,设运动的时间为t s.
备用图
(1)运动2 s 后,求PQ 的长.
(2)当点Q 在边BC上运动时,运动几秒后,△PQB是等腰三角形
(3)当点Q 在边CA 上运动时,求能使△BCQ是等腰三角形的运动时间.
第十七章检测卷
1.D 2.B 3.D 4.B 5.B 6.B 7.A 8.A 9.D 10.A 11.5√2 12.45 13.3cm 14.6 15.45°
16. 解:(1)∵∠C=90°,AB=15,AC=12, ∴BC===9.
(2) ∵∠C=90°,AB=6, ∠A=30°,
17. 解:(1)如图①,△ABC 即为所求.
(2)如图②,△ABC 即为所求.
图②
18. 解:(1)∵DA⊥AB,AC=60m,AB=80m, ∴BC===100(m).
答:入口B 到大摆锤 C 的距离为100m.
(2)①DE⊥EC
②∵∠DEC=90°,CD=75m,CE=45m, ∴DE===60(m).
答:过山车D 到旋转木马E 的距离为60 m.
19.解:∵C,D 两村到公交车站 E 的距离相等, ∴DE=EC.
∵DA⊥AB,CB⊥AB,
∴∠A=∠B=90°.
∴AE +AD =DE ,BE +BC =EC .
∴AE +AD =BE +BC .
设 AE=x km,则 BE=AB-AE=(17-x)km.
∵DA=12 km,CB=5 km,
∴x +12 =(17-x) +5 .
解得x=5.∴AE=5km.
答:公交车站E 应建在离点A 5km处 .
20. (1)证明:如图,连接AC.
∵∠B=90°,
∴AC =AB +BC =20 +15 =625 . ∵AD +CD =24 +7 =625,
∴AC =AD +CD .
∴△ADC 是直角三角形,∠D=90°.
∴CD⊥AD.
(2)解:S四边形ABCD=S△ABc+S△ADC
=234
21.解:(1)不正确.
由题意,得AG=CD=1m,GC=AD=15m,∠AGC=∠BGC=90° . 设BG=xm, 则BC=(26-1-x)m.
在 Rt△BGC中,由勾股定理,得BG +CG =CB , 即 x +15 =(26-1-x) .
解得x=8.∴BG=8m.
∴AB=BG+GA=9(m).
∴立柱AB 段的正确长度为9m.
(2)由题意,得 CF=DE=3m, ∴GF=GC+CF=18(m).
在 Rt△BGF 中,由勾股定理,得 BF== =(m).
∴钢索BF 的长为m.
22. 解:(1)④
⑤如图,连接AB, 交 CD于点O', 则此时A0+BO 取得最 小值,延长AC 到点A′, 连接A'B, 使四边形A'CDB 是长 方形,则∠A'=90°,A'C=BD=9.
∴AB===20.
∴A0+BO 的最小值,即代数式 ++81 的最小值为20.
(2)10 [提示]如图,作线段ED=8,C 为线段ED 上一点,且CE=2. 过点C 在线段 CD的上方作线段CD的垂线 AC, 使AC=5; 过点D 在线段CD的下方作线段CD的 垂线BD, 使 BD=3. 连接AB,交 CD于点0,如图所示.
设 OE=x, 则CO=x-2,DO=8-x.
23. 解:(1)当t=2 时 ,AP=2cm,BQ=2t=4cm ∵AB=16cm, ∴BP=AB-AP=16-2=14(cm). ∴PQ===(cm).
(2)由题意,可知AP=t cm,BQ=2t cm. ∵AB=16cm, ∴BP=AB-AP=(16-t)cm.
当△PQB 为等腰三角形时,BP=BQ, 即16-t=2t.
解得
∴运云后,△ PQB 是等腰三角形.
(3)①当CQ=BQ 时,如图所示,则∠C=∠CBQ.
∵∠ABC=90°,
∴∠CBQ+∠ABQ=90°,∠A+∠C=90°. ∴∠A=∠ABQ. ∴BQ=AQ. CQ=AQ ∵AC===20(cm), ∴CQ=AQ=10 cm. ∴BC+CQ=22 cm. ∴t=22÷2=11.
②当CQ=BC 时,如图所示.
此时BC+CQ=24 cm. ∴t=24÷2=12.
③ 当BC=BQ 时,如图所示,过点B 作 BE⊥AC于点E
则(cm)
∴
∴CQ=2CE=14.4cm.∴BC+CQ=26.4 cm.
∴t=26.4÷2=13.2.
综上所述,当运动时间为11s 或 12s 或13.2s 时 ,△BCQ 是等腰三角形.
