第十八章 平行四边形 检测卷(含答案)2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第十八章 平行四边形 检测卷(含答案)2024-2025学年人教版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 212.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 20:46:06 | ||
图片预览




文档简介
第十八章 平行四边形 检测卷
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B. 互相平分
C. 互相垂直 D. 互相垂直且相等
2. □ABCD 中,∠A 比∠B 大20°,则∠C 的度数为 ( ) A.100° B.80° C.60° D.120°
3.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为 ( )
A.4,8,4,8 B.5,7,5,7
C.5.5,6.5,5.5,6.5 D.3,9,3,9
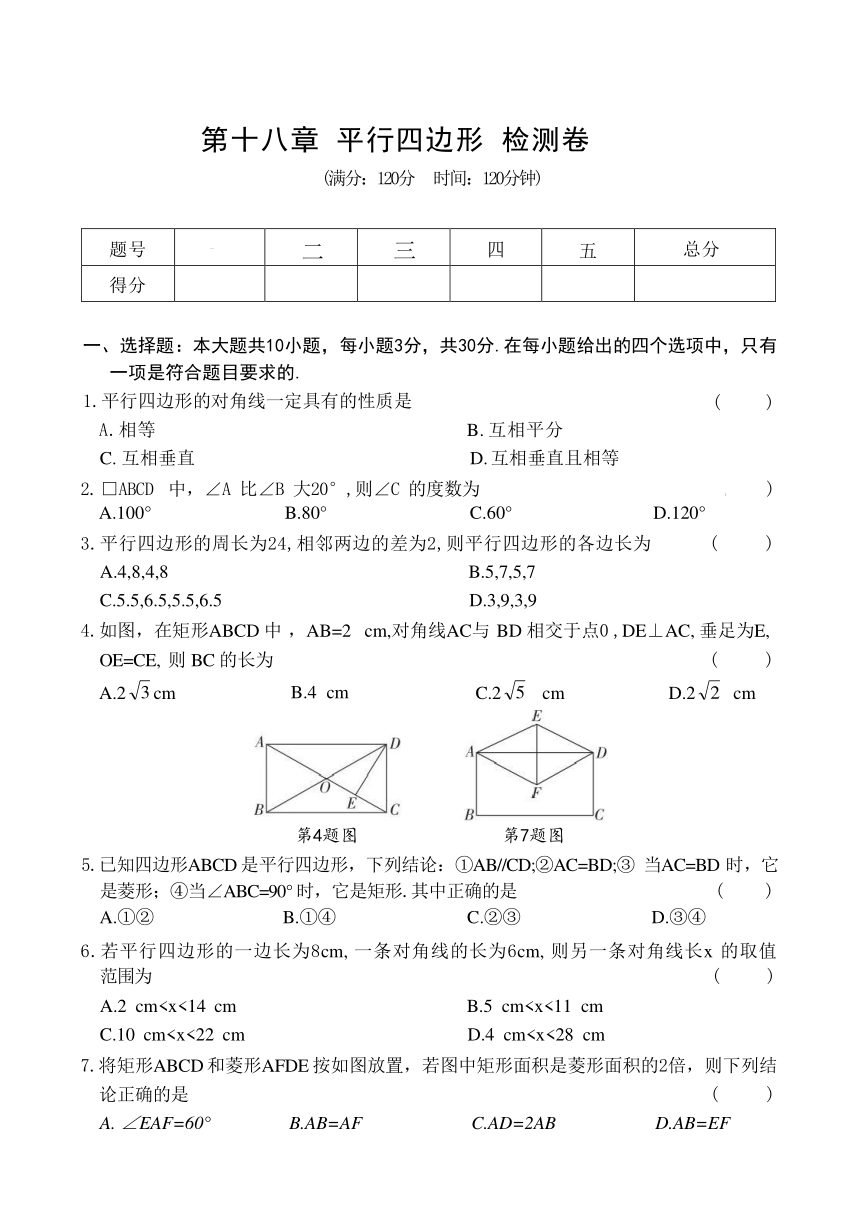
4.如图,在矩形ABCD 中 ,AB=2 cm,对角线AC与 BD 相交于点0 ,DE⊥AC, 垂足为E, OE=CE, 则 BC 的长为 ( )
A.2cm B.4 cm C.2 cm D.2 cm
第4题图 第7题图
5.已知四边形ABCD 是平行四边形,下列结论:①AB//CD;②AC=BD;③ 当AC=BD 时,它 是菱形;④当∠ABC=90° 时,它是矩形.其中正确的是 ( ) A.①② B.①④ C.②③ D.③④
6.若平行四边形的一边长为8cm, 一条对角线的长为6cm, 则另一条对角线长x 的取值 范围为 ( )
A.2 cmC.10 cm7.将矩形ABCD 和菱形AFDE 按如图放置,若图中矩形面积是菱形面积的2倍,则下列结 论正确的是 ( )
A. ∠EAF=60° B.AB=AF C.AD=2AB D.AB=EF
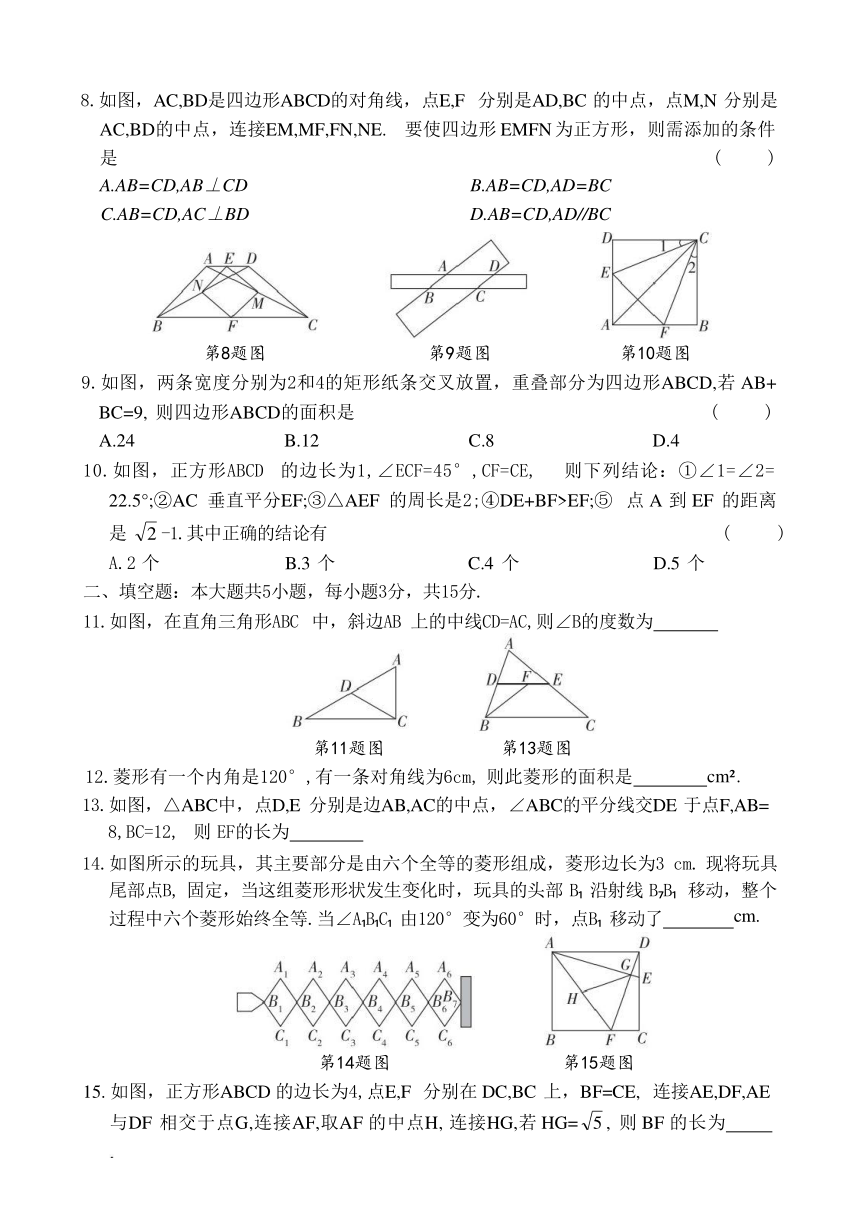
8.如图,AC,BD是四边形ABCD的对角线,点E,F 分别是AD,BC 的中点,点M,N 分别是 AC,BD的中点,连接EM,MF,FN,NE. 要使四边形 EMFN 为正方形,则需添加的条件 是 ( )
A.AB=CD,AB⊥CD B.AB=CD,AD=BC
C.AB=CD,AC⊥BD D.AB=CD,AD//BC
第8题图
第9题图
第10题图
9.如图,两条宽度分别为2和4的矩形纸条交叉放置,重叠部分为四边形ABCD,若 AB+ BC=9, 则四边形ABCD的面积是 ( ) A.24 B.12 C.8 D.4
10.如图,正方形ABCD 的边长为1,∠ECF=45°,CF=CE, 则下列结论:①∠1=∠2= 22.5°;②AC 垂直平分EF;③△AEF 的周长是2;④DE+BF>EF;⑤ 点 A 到 EF 的距离 是 -1.其中正确的结论有 ( ) A.2 个 B.3 个 C.4 个 D.5 个
二、填空题:本大题共5小题,每小题3分,共15分.
11.如图,在直角三角形ABC 中,斜边AB 上的中线CD=AC,则∠B的度数为
第11题图 第13题图
12.菱形有一个内角是120°,有一条对角线为6cm, 则此菱形的面积是 cm .
13.如图,△ABC中,点D,E 分别是边AB,AC的中点,∠ABC的平分线交DE 于点F,AB= 8,BC=12, 则 EF的长为
14.如图所示的玩具,其主要部分是由六个全等的菱形组成,菱形边长为3 cm. 现将玩具 尾部点B, 固定,当这组菱形形状发生变化时,玩具的头部 B 沿射线 B B 移动,整个 过程中六个菱形始终全等.当∠A B C 由120°变为60°时,点B 移动了 cm.
第14题图 第15题图
15. 如图,正方形ABCD 的边长为4,点E,F 分别在 DC,BC 上,BF=CE, 连接AE,DF,AE 与DF 相交于点G,连接AF,取AF 的中点H, 连接HG,若 HG=, 则 BF 的长为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16. 在四边形ABCD 中,对角线AC,BD 相交于点0,已知AD=12,OD=OB=5,AC=26,
∠ADB=90°.求证:四边形ABCD为平行四边形.
17.如图,四边形ABCD 是菱形,点E,F 分别在AB 和 AD 上,且 BE=DF. 点 G,H 分别在
CD和 BC 上,且 EG//AD,FH//AB,EG 与 FH 相交于点M.求证:四边形AEMF为菱形.
18.如图,四边形ABCD 是矩形.
(1)尺规作图:作∠ABC 的平分线交AD 于点E,连接CE; (不写作法,保留作图痕迹)
(2)在(1)的条件下,若 BE=CE=2, 求AD的长.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,四边形ABCD 是菱形,AC=8,BD=6,DH⊥AB于点H,BG⊥CD于点G.
(1)求DH的长;
(2)求四边形DHBG的面积.
20.如图,△ABC是边长为a 的等边三角形,P 是△ABC内的任意一点,过点P 作 EF//AB 分别交 AC,BC 于点E,F; 过点P 作 GH//BC 分别交AB,AC 于点 G,H; 过点P 作 MN// AC分别交AB,BC 于点M,N. 试猜想EF+GH+MN的值是多少 其值是否随点P 位置 的改变而改变 并说明理由.
21.如图①,在正方形ABCD中,对角线交于点0,E 是 OB 上一点,连接AE, 作 DG⊥AE 于 点 G,DG交 OA于点F.
(1)求证:OE=OF;
(2)如图②,当E 为 OB 延长线上一点时,画出对应的图形.观察(1)中的结论是否仍 然成立,并说明理由.
(
图
②
)图①
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.综合与实践
综合与实践课上,老师带领同学们以“正方形和矩形的折叠”为主题开展数学活动.
图①
图②
(1)操作判断
操作一:将正方形纸片 ABCD 依次沿对角线AC,BD 对折,把纸片展平,折痕的交点 为0;
操作二:在AB上取一点E, 在 BC 上取一点F, 沿 EF 折叠,使点B 落在点0处,然后 延长 EO 交 DC于点G, 连接 FG.
如图①是经过以上两次操作后得到的图形,判断线段EF和 FG 的数量关系并说明 理由.
(2)迁移思考
图②是把矩形纸片ABCD 按照(1)中的操作一和操作二得到的图形.请判断AE,EF, CF 三条线段之间有什么数量关系 并仅就图②证明你的判断.
23. 在平行四边形ABCD中 ,AB=6cm,BC=acm,P是对角线AC 上的一个动点,由A 向 C 运动(不与点A,C 重合),速度为1 cm/s,Q 是 CB 延长线上一点,以与点P相同的速 度由 B 向CB 延长线方向运动(不与点B 重合),连接PQ 交 AB 于点E.
(1)如图①,若∠ABC=60°,BC=AB, 求点P运动几秒后,∠BQE=30° .
(2)如图②,在(1)的条件下,作PF⊥AB 于点F, 在运动过程中,线段EF 的长度是否 发生变化 如果不变,求出 EF 的长;如果变化,请说明理由.
(3)如图③,当平行四边形ABCD 的面积是24cm 时,是否存在某个 a的值,使 QE= PE 若存在,求出 a 的值;若不存在,说明理由.
第十八章检测卷
1.B 2.A 3.B 4.A 5.B 6.C 7.D 8.A 9.B
10.C 11.30°12.6或18 13.2 14.(18-18) 15.2
16. 证明:∵AD=12,OD=5,∠ADB=90°,
∴A0==13.
∵AC=26, ∴AO=0C=13.
又 OD=OB, 四边形ABCD 为平行四边形.
17. 证明:∵ EG//AD,FH//AB,
∴四边形AEMF 为平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∵BE=DF,
∴AB-BE=AD-DF, 即AE=AF.
∴四边形AEMF为菱形.
18.解:(1)如图即为所求.
(2)∵四边形ABCD为矩形, ∴BC=AD,∠ABC=90°.
∵BE 平分∠ABC,
∴∠ABE=∠EBC=∠ABC=45°
∵BE=CE=2,
∴∠EBC=∠ECB=45°.
∴∠BEC=90°.
∴BC =2BE =8.
∴BC=. ∴AD=.
19.解:(1)∵四边形ABCD 是菱形, ∴AC⊥BD,OA=OC=4,OB=OD=3. ∴AB==5.
(2)∵四边形ABCD是菱形,∴AB//CD. ∵DH⊥AB, ∴DH⊥CD.
又 BG⊥CD,
∴∠DHB=∠HDG=∠DGB=90°. ∴四边形DHBG为矩形.
,BD=6,
∴四边形DHBG的面积为1
20. 解 :EF+GH+MN=2a,EF+GH+MN 的值不随点P 位置的
改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60° .
∵GH//BC, ∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形. ∴ GH=AG=AM+MG.① 同理,可得△BMN 是等边三角形,
∴MN=MB=MG+GB.②
∵MN//AC,EF//AB,
∴四边形AMPE是平行四边形. PE=AM.
同理,可得四边形BFPG 是平行四边形,
∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得EF+GH+MN=(AM+GB)+(AM+MG)+(MG+ GB)=2(AM+MG+GB)=2AB=2a.
21. (1)证明:∵四边形ABCD是正方形, ∴OA=OD,AC⊥BD.
∴∠DOF=∠AOE=90°. ∴∠OAE+∠OEA=90°.
∵DG⊥AE,
∴∠ODF+∠OEA=90°. ∴∠ODF=∠OAE.
在△OAE和△ODF 中 , ∴△OAE≌△ODF(ASA). ∴OE=OF.
(2)解:画出对应的图形如图②所示,(1)中的结论仍然
成立.理由如下:
同(1),得∠ODF=∠OAE. 在△OAE和△ODF中 ,
∴△OAE≌△ODF(ASA).
∴OE=OF.
22.解:(1)EF=FG. 理由如下:
∵四边形 ABCD 为正方形,点0为对角线AC,BD 的交点,
∴OA=OC,∠OAE=∠OCG=45°,∠ABC=90°.
在△OAE和△OCG中 ,
∴△OAE≌△OCG(ASA).
∴OE=OG.
由折叠的性质,得∠EOF=∠ABC=90°, 即 OF⊥EG.
∴OF 垂直平分EG.
∴EF=FG.
(2)AE +CF =EF . 证明如下:
∵四边形ABCD为矩形,点0为对角线AC,BD 的交点, ∴AB//CD,0A=0C, ∠ABC=90°.
∴∠OAE=∠OCG.
在△OAE和△OCG中 ,
∴△OAE≌△OCG(ASA).
∴AE=CG,OE=OG.
由折叠的性质,得∠EOF=∠ABC=90°, 即 OF⊥EG.
∴OF 垂直平分EG.
∴EF=FG.
在 Rt△FCG中,由勾股定理,得CG +CF =FG , 即 AE +CF =EF .
23. 解:(1)设点P 运动ts 后,∠BQE=30°, 则AP=BQ=t cm. ∵∠ABC=60°,BC=AB, △ABC 为等边三角形.
∴AB=BC=AC=6cm, ∠ACB=60°.
∴PC=(6-t)cm,QC=(6+t)cm.
∵∠BQE=30°,∠ACB=60°, ∴∠QPC=90°.
∴QC=2PC.
∴6+t=2(6-t). 解得t=2∵ 点 P 运动2s 后,∠BQE=30° .
(2)如图②,过点P 作 PG//BC,与AB 交于点G,则∠PGE= ∠QBE,∠EPG=∠EQB,∠AGP=∠ABC=60°.
由(1),可得∠BAC=60°, ∴△AGP为等边三角形. ∴GP=AP=AG.
∵BQ=AP, ∴GP=BQ.
∴△PEG≌△QEB(ASA).
∴GE=BE.
∵△APG 是等边三角形,PF⊥AB,∴AF=GF.
故在运动过程中,线段EF 的长度不变,EF的长为3cm.
(3)如图③,过点P 作 PG//BC, 与 AB交于点G, 过 点C 作 CH⊥AB于点H, 则∠PGE=∠QBE,∠EPG=∠EQB. ∵PE=QE,
∴△PEG≌△QEB(AAS). ∴GP=BQ.
∵BQ=AP, ∴GP=AP ∴∠PGA=∠PAG.
∵GP//BC, ∴.AGP=∠ABC. ∴∠PAG=∠ABC.
∴CA=CB=acm.
∵平行四边形 ABCD 的面积是24 cm ,AB=6 cm, CH⊥AB,
∴AH=BH=3 cm,CH=4 cm.
∴BC=AC===5(cm). ∴a=5.
故在运动中存在某一时刻,使QE=PE, 此时a 的值为5.
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.平行四边形的对角线一定具有的性质是 ( )
A.相等 B. 互相平分
C. 互相垂直 D. 互相垂直且相等
2. □ABCD 中,∠A 比∠B 大20°,则∠C 的度数为 ( ) A.100° B.80° C.60° D.120°
3.平行四边形的周长为24,相邻两边的差为2,则平行四边形的各边长为 ( )
A.4,8,4,8 B.5,7,5,7
C.5.5,6.5,5.5,6.5 D.3,9,3,9
4.如图,在矩形ABCD 中 ,AB=2 cm,对角线AC与 BD 相交于点0 ,DE⊥AC, 垂足为E, OE=CE, 则 BC 的长为 ( )
A.2cm B.4 cm C.2 cm D.2 cm
第4题图 第7题图
5.已知四边形ABCD 是平行四边形,下列结论:①AB//CD;②AC=BD;③ 当AC=BD 时,它 是菱形;④当∠ABC=90° 时,它是矩形.其中正确的是 ( ) A.①② B.①④ C.②③ D.③④
6.若平行四边形的一边长为8cm, 一条对角线的长为6cm, 则另一条对角线长x 的取值 范围为 ( )
A.2 cm
A. ∠EAF=60° B.AB=AF C.AD=2AB D.AB=EF
8.如图,AC,BD是四边形ABCD的对角线,点E,F 分别是AD,BC 的中点,点M,N 分别是 AC,BD的中点,连接EM,MF,FN,NE. 要使四边形 EMFN 为正方形,则需添加的条件 是 ( )
A.AB=CD,AB⊥CD B.AB=CD,AD=BC
C.AB=CD,AC⊥BD D.AB=CD,AD//BC
第8题图
第9题图
第10题图
9.如图,两条宽度分别为2和4的矩形纸条交叉放置,重叠部分为四边形ABCD,若 AB+ BC=9, 则四边形ABCD的面积是 ( ) A.24 B.12 C.8 D.4
10.如图,正方形ABCD 的边长为1,∠ECF=45°,CF=CE, 则下列结论:①∠1=∠2= 22.5°;②AC 垂直平分EF;③△AEF 的周长是2;④DE+BF>EF;⑤ 点 A 到 EF 的距离 是 -1.其中正确的结论有 ( ) A.2 个 B.3 个 C.4 个 D.5 个
二、填空题:本大题共5小题,每小题3分,共15分.
11.如图,在直角三角形ABC 中,斜边AB 上的中线CD=AC,则∠B的度数为
第11题图 第13题图
12.菱形有一个内角是120°,有一条对角线为6cm, 则此菱形的面积是 cm .
13.如图,△ABC中,点D,E 分别是边AB,AC的中点,∠ABC的平分线交DE 于点F,AB= 8,BC=12, 则 EF的长为
14.如图所示的玩具,其主要部分是由六个全等的菱形组成,菱形边长为3 cm. 现将玩具 尾部点B, 固定,当这组菱形形状发生变化时,玩具的头部 B 沿射线 B B 移动,整个 过程中六个菱形始终全等.当∠A B C 由120°变为60°时,点B 移动了 cm.
第14题图 第15题图
15. 如图,正方形ABCD 的边长为4,点E,F 分别在 DC,BC 上,BF=CE, 连接AE,DF,AE 与DF 相交于点G,连接AF,取AF 的中点H, 连接HG,若 HG=, 则 BF 的长为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16. 在四边形ABCD 中,对角线AC,BD 相交于点0,已知AD=12,OD=OB=5,AC=26,
∠ADB=90°.求证:四边形ABCD为平行四边形.
17.如图,四边形ABCD 是菱形,点E,F 分别在AB 和 AD 上,且 BE=DF. 点 G,H 分别在
CD和 BC 上,且 EG//AD,FH//AB,EG 与 FH 相交于点M.求证:四边形AEMF为菱形.
18.如图,四边形ABCD 是矩形.
(1)尺规作图:作∠ABC 的平分线交AD 于点E,连接CE; (不写作法,保留作图痕迹)
(2)在(1)的条件下,若 BE=CE=2, 求AD的长.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.如图,四边形ABCD 是菱形,AC=8,BD=6,DH⊥AB于点H,BG⊥CD于点G.
(1)求DH的长;
(2)求四边形DHBG的面积.
20.如图,△ABC是边长为a 的等边三角形,P 是△ABC内的任意一点,过点P 作 EF//AB 分别交 AC,BC 于点E,F; 过点P 作 GH//BC 分别交AB,AC 于点 G,H; 过点P 作 MN// AC分别交AB,BC 于点M,N. 试猜想EF+GH+MN的值是多少 其值是否随点P 位置 的改变而改变 并说明理由.
21.如图①,在正方形ABCD中,对角线交于点0,E 是 OB 上一点,连接AE, 作 DG⊥AE 于 点 G,DG交 OA于点F.
(1)求证:OE=OF;
(2)如图②,当E 为 OB 延长线上一点时,画出对应的图形.观察(1)中的结论是否仍 然成立,并说明理由.
(
图
②
)图①
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.综合与实践
综合与实践课上,老师带领同学们以“正方形和矩形的折叠”为主题开展数学活动.
图①
图②
(1)操作判断
操作一:将正方形纸片 ABCD 依次沿对角线AC,BD 对折,把纸片展平,折痕的交点 为0;
操作二:在AB上取一点E, 在 BC 上取一点F, 沿 EF 折叠,使点B 落在点0处,然后 延长 EO 交 DC于点G, 连接 FG.
如图①是经过以上两次操作后得到的图形,判断线段EF和 FG 的数量关系并说明 理由.
(2)迁移思考
图②是把矩形纸片ABCD 按照(1)中的操作一和操作二得到的图形.请判断AE,EF, CF 三条线段之间有什么数量关系 并仅就图②证明你的判断.
23. 在平行四边形ABCD中 ,AB=6cm,BC=acm,P是对角线AC 上的一个动点,由A 向 C 运动(不与点A,C 重合),速度为1 cm/s,Q 是 CB 延长线上一点,以与点P相同的速 度由 B 向CB 延长线方向运动(不与点B 重合),连接PQ 交 AB 于点E.
(1)如图①,若∠ABC=60°,BC=AB, 求点P运动几秒后,∠BQE=30° .
(2)如图②,在(1)的条件下,作PF⊥AB 于点F, 在运动过程中,线段EF 的长度是否 发生变化 如果不变,求出 EF 的长;如果变化,请说明理由.
(3)如图③,当平行四边形ABCD 的面积是24cm 时,是否存在某个 a的值,使 QE= PE 若存在,求出 a 的值;若不存在,说明理由.
第十八章检测卷
1.B 2.A 3.B 4.A 5.B 6.C 7.D 8.A 9.B
10.C 11.30°12.6或18 13.2 14.(18-18) 15.2
16. 证明:∵AD=12,OD=5,∠ADB=90°,
∴A0==13.
∵AC=26, ∴AO=0C=13.
又 OD=OB, 四边形ABCD 为平行四边形.
17. 证明:∵ EG//AD,FH//AB,
∴四边形AEMF 为平行四边形.
∵四边形ABCD是菱形,
∴AB=AD.
∵BE=DF,
∴AB-BE=AD-DF, 即AE=AF.
∴四边形AEMF为菱形.
18.解:(1)如图即为所求.
(2)∵四边形ABCD为矩形, ∴BC=AD,∠ABC=90°.
∵BE 平分∠ABC,
∴∠ABE=∠EBC=∠ABC=45°
∵BE=CE=2,
∴∠EBC=∠ECB=45°.
∴∠BEC=90°.
∴BC =2BE =8.
∴BC=. ∴AD=.
19.解:(1)∵四边形ABCD 是菱形, ∴AC⊥BD,OA=OC=4,OB=OD=3. ∴AB==5.
(2)∵四边形ABCD是菱形,∴AB//CD. ∵DH⊥AB, ∴DH⊥CD.
又 BG⊥CD,
∴∠DHB=∠HDG=∠DGB=90°. ∴四边形DHBG为矩形.
,BD=6,
∴四边形DHBG的面积为1
20. 解 :EF+GH+MN=2a,EF+GH+MN 的值不随点P 位置的
改变而改变.理由如下:
∵△ABC是等边三角形,∴∠A=∠B=∠C=60° .
∵GH//BC, ∴∠AGH=∠B=60°,∠AHG=∠C=60°.
∴△AGH是等边三角形. ∴ GH=AG=AM+MG.① 同理,可得△BMN 是等边三角形,
∴MN=MB=MG+GB.②
∵MN//AC,EF//AB,
∴四边形AMPE是平行四边形. PE=AM.
同理,可得四边形BFPG 是平行四边形,
∴PF=GB.
∴EF=PE+PF=AM+GB.③
由①②③,得EF+GH+MN=(AM+GB)+(AM+MG)+(MG+ GB)=2(AM+MG+GB)=2AB=2a.
21. (1)证明:∵四边形ABCD是正方形, ∴OA=OD,AC⊥BD.
∴∠DOF=∠AOE=90°. ∴∠OAE+∠OEA=90°.
∵DG⊥AE,
∴∠ODF+∠OEA=90°. ∴∠ODF=∠OAE.
在△OAE和△ODF 中 , ∴△OAE≌△ODF(ASA). ∴OE=OF.
(2)解:画出对应的图形如图②所示,(1)中的结论仍然
成立.理由如下:
同(1),得∠ODF=∠OAE. 在△OAE和△ODF中 ,
∴△OAE≌△ODF(ASA).
∴OE=OF.
22.解:(1)EF=FG. 理由如下:
∵四边形 ABCD 为正方形,点0为对角线AC,BD 的交点,
∴OA=OC,∠OAE=∠OCG=45°,∠ABC=90°.
在△OAE和△OCG中 ,
∴△OAE≌△OCG(ASA).
∴OE=OG.
由折叠的性质,得∠EOF=∠ABC=90°, 即 OF⊥EG.
∴OF 垂直平分EG.
∴EF=FG.
(2)AE +CF =EF . 证明如下:
∵四边形ABCD为矩形,点0为对角线AC,BD 的交点, ∴AB//CD,0A=0C, ∠ABC=90°.
∴∠OAE=∠OCG.
在△OAE和△OCG中 ,
∴△OAE≌△OCG(ASA).
∴AE=CG,OE=OG.
由折叠的性质,得∠EOF=∠ABC=90°, 即 OF⊥EG.
∴OF 垂直平分EG.
∴EF=FG.
在 Rt△FCG中,由勾股定理,得CG +CF =FG , 即 AE +CF =EF .
23. 解:(1)设点P 运动ts 后,∠BQE=30°, 则AP=BQ=t cm. ∵∠ABC=60°,BC=AB, △ABC 为等边三角形.
∴AB=BC=AC=6cm, ∠ACB=60°.
∴PC=(6-t)cm,QC=(6+t)cm.
∵∠BQE=30°,∠ACB=60°, ∴∠QPC=90°.
∴QC=2PC.
∴6+t=2(6-t). 解得t=2∵ 点 P 运动2s 后,∠BQE=30° .
(2)如图②,过点P 作 PG//BC,与AB 交于点G,则∠PGE= ∠QBE,∠EPG=∠EQB,∠AGP=∠ABC=60°.
由(1),可得∠BAC=60°, ∴△AGP为等边三角形. ∴GP=AP=AG.
∵BQ=AP, ∴GP=BQ.
∴△PEG≌△QEB(ASA).
∴GE=BE.
∵△APG 是等边三角形,PF⊥AB,∴AF=GF.
故在运动过程中,线段EF 的长度不变,EF的长为3cm.
(3)如图③,过点P 作 PG//BC, 与 AB交于点G, 过 点C 作 CH⊥AB于点H, 则∠PGE=∠QBE,∠EPG=∠EQB. ∵PE=QE,
∴△PEG≌△QEB(AAS). ∴GP=BQ.
∵BQ=AP, ∴GP=AP ∴∠PGA=∠PAG.
∵GP//BC, ∴.AGP=∠ABC. ∴∠PAG=∠ABC.
∴CA=CB=acm.
∵平行四边形 ABCD 的面积是24 cm ,AB=6 cm, CH⊥AB,
∴AH=BH=3 cm,CH=4 cm.
∴BC=AC===5(cm). ∴a=5.
故在运动中存在某一时刻,使QE=PE, 此时a 的值为5.
