第十九章 一次函数 检测卷(含答案) 2024-2025学年人教版数学八年级下册
文档属性
| 名称 | 第十九章 一次函数 检测卷(含答案) 2024-2025学年人教版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 268.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-07-14 16:29:42 | ||
图片预览



文档简介
第十九章 一次函数 检测卷
(满分:120分 时间:120分钟)
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.在圆周长的计算公式C=2πr 中,变量有 ( ) A.C,π B.C,r C.π,r D.2π,r
2.若正比例函数y=kx 的图象经过点(-2,3),则 k 的值为 ( )
B D
3.若点A(-5,y ) 和 B(-3,y ) 都在直线y=-3x+2 上,则y 与y 的关系是 ( ) A.y ≤y B.y =y C.yy
4.将一次函数y=2x 的图象沿y 轴向上平移5个单位长度,所得直线的解析式为( ) A.y=2x-5 B.y=2x+5 C.y=2x+8 D.y=2x-8
5.关于函数y=-2x+1, 下列结论正确的是 ( )
A.图象必经过点(-2,1) B.图象经过第一、二、三象限
C. 当 时 ,y<0 D.y 随x 的增大而增大
6.如图所示,函数y =ax+b 和y =|x| 的图象相交于(-1,1),(2,2)两点.当y >y 时 ,x 的取值范围是 ( )
A.x<-1 B.-12 D.x<-1 或 x>2
7.如果一次函数y=kx+k+1的图象经过第一、二、四象限,则 k 的取值范围是 ( ) A.k>-1 B.k<-1 C.k<0 D.-18.对任意实数a, 直线y=(a-1)x+3-2a 一定经过点 ( )
A.(0,1) B.(1,2) C.(2,1) D.(3,0)
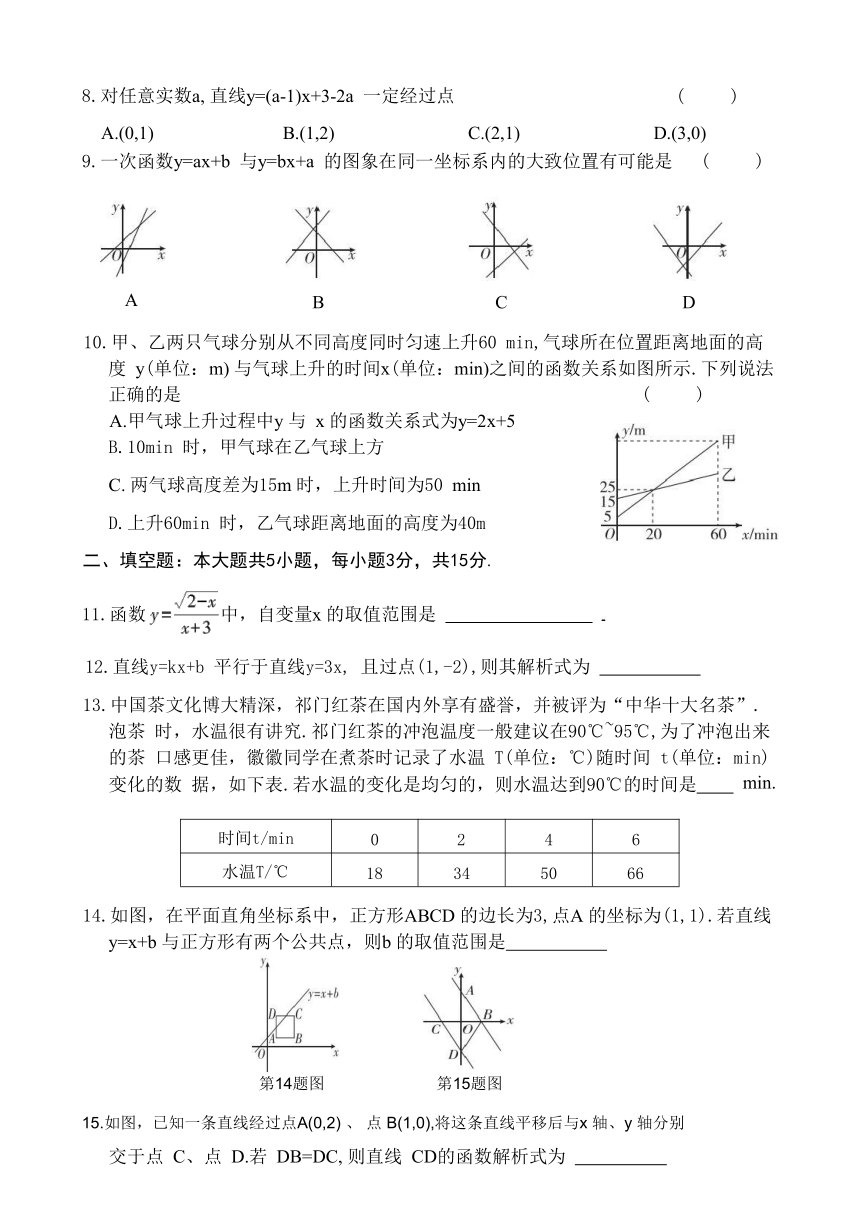
9.一次函数y=ax+b 与y=bx+a 的图象在同一坐标系内的大致位置有可能是 ( )
A
B
C
D
10.甲、乙两只气球分别从不同高度同时匀速上升60 min,气球所在位置距离地面的高度 y(单位:m) 与气球上升的时间x(单位:min)之间的函数关系如图所示.下列说法正确的是 ( )
A.甲气球上升过程中y 与 x 的函数关系式为y=2x+5 B.10min 时,甲气球在乙气球上方
C. 两气球高度差为15m 时,上升时间为50 min
D.上升60min 时,乙气球距离地面的高度为40m
二、填空题:本大题共5小题,每小题3分,共15分.
11.函数中,自变量x 的取值范围是
12.直线y=kx+b 平行于直线y=3x, 且过点(1,-2),则其解析式为
13.中国茶文化博大精深,祁门红茶在国内外享有盛誉,并被评为“中华十大名茶”.泡茶 时,水温很有讲究.祁门红茶的冲泡温度一般建议在90℃~95℃,为了冲泡出来的茶 口感更佳,徽徽同学在煮茶时记录了水温 T(单位:℃)随时间 t(单位:min)变化的数 据,如下表.若水温的变化是均匀的,则水温达到90℃的时间是 min.
时间t/min 0 2 4 6
水温T/℃ 18 34 50 66
14.如图,在平面直角坐标系中,正方形ABCD 的边长为3,点A 的坐标为(1,1).若直线 y=x+b 与正方形有两个公共点,则b 的取值范围是
第14题图 第15题图
15.如图,已知一条直线经过点A(0,2) 、 点 B(1,0),将这条直线平移后与x 轴、y 轴分别
交于点 C、点 D.若 DB=DC, 则直线 CD的函数解析式为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.已知关于x 的函数y=(m-1)x-(3m+1).
(1)若函数为正比例函数,求m 的值;
(2)若y 随 x 的增大而减小,求 m 的取值范围.
17.游泳池应定期换水,某游泳池在一次换水前存水936 m ,换水时关闭进水孔打开排水孔,当放水时间增加时,游泳池的存水随之减少.设放水时间为th, 游泳池的存水量为 Qm , 它们的变化情况如表:
放水时间t/h 0 1 2 3 4 5
游泳池的存水量Q/m 936 858 780 702 a 546
(1)在这个变化过程中,自变量是
(2)上述表格中,a= ,并写出 Q 与 t的关系式.
(3)放完游泳池里的水共需要多长时间
18.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数 y=k1x+b 和 y=kx+b 的图象,分别与x 轴交于点A,B, 两直线交于点C. 已知点A(-1, 0),B(2,0), 观察图象并回答下列问题:
(1)关于x 的方程k1x+b1=0 的解是 ;关于x 的不等式 kx+b<0 的解集是 ;
(2)直接写出关于x 的不等式 的解集;
(3)若点C(1,3), 求关于x 的不等式k1x+b1>x+b 的解集.
四、解答题(二):本大题共3小题,每小题9分,共27分.
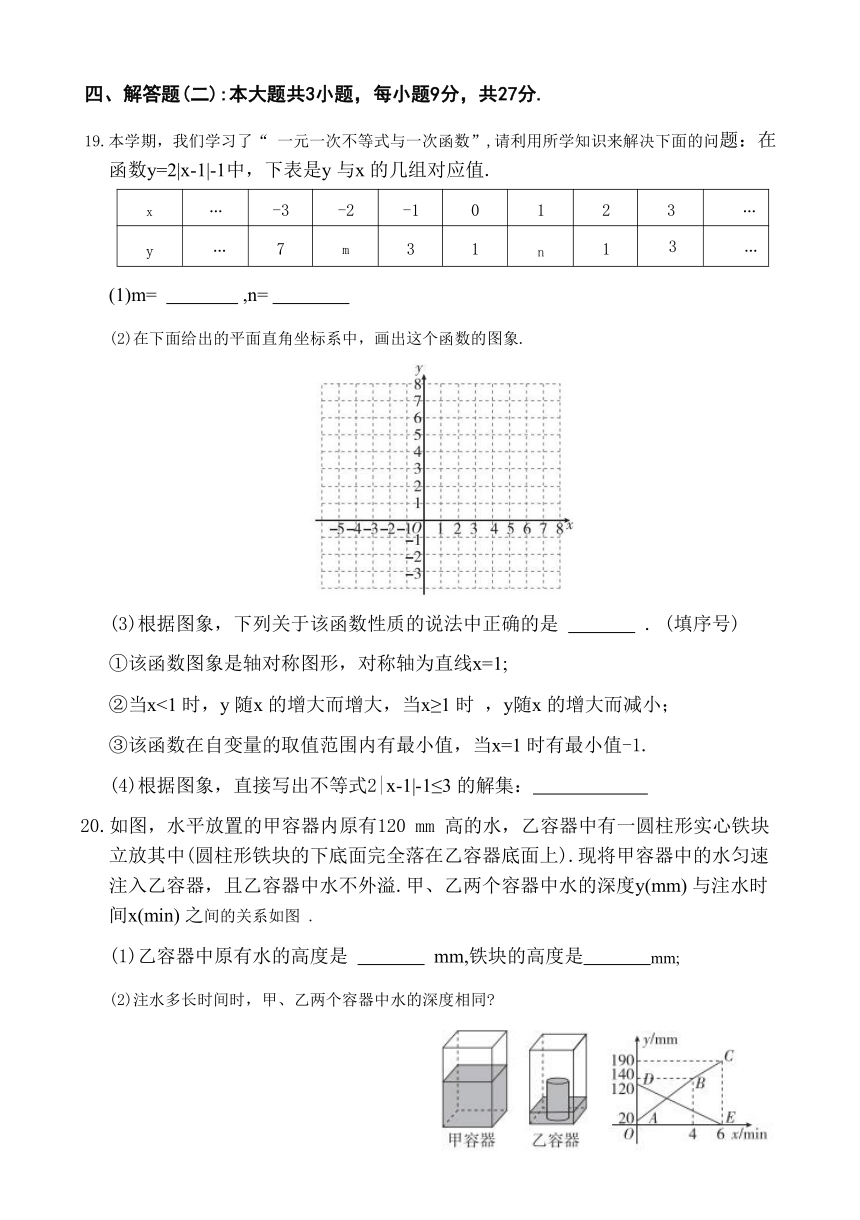
19.本学期,我们学习了“ 一元一次不等式与一次函数”,请利用所学知识来解决下面的问题:在函数y=2|x-1|-1中,下表是y 与x 的几组对应值.
x … -3 -2 -1 0 1 2 3 …
y … 7 m 3 1 n 1 3 …
(1)m= ,n=
(2)在下面给出的平面直角坐标系中,画出这个函数的图象.
(3)根据图象,下列关于该函数性质的说法中正确的是 . (填序号)
①该函数图象是轴对称图形,对称轴为直线x=1;
②当x<1 时,y 随x 的增大而增大,当x≥1 时 ,y随x 的增大而减小;
③该函数在自变量的取值范围内有最小值,当x=1 时有最小值-1.
(4)根据图象,直接写出不等式2|x-1|-1≤3 的解集:
20.如图,水平放置的甲容器内原有120 mm 高的水,乙容器中有一圆柱形实心铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上).现将甲容器中的水匀速注入乙容器,且乙容器中水不外溢.甲、乙两个容器中水的深度y(mm) 与注水时间x(min) 之间的关系如图 .
(1)乙容器中原有水的高度是 mm,铁块的高度是 mm;
(2)注水多长时间时,甲、乙两个容器中水的深度相同
21.“五 ·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.甲公司收费:按日收取固定租金80元,另外再按出租时间计费;乙公司收费:无固定租金,直接以租车时间计费,每小时的租金是30元.
(1)设租车时间为xh, 租用甲公司的车所需费用为y 元,租用乙公司的车所需费用 为y 元,分别求出y ,y 关于x 的函数解析式;
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记 录,并根据所记录的数据绘制函数图象,其中日销售量y(kg) 与销售时间x(天)之间 的函数关系如图①所示,销售单价p(元/kg)与销售时间x(天)之间的部分函数关系 如图②所示.
(1)直接写出y 与x 之间的函数关系式.
(2)分别求出第10天和第15天的销售金额.
(3)若日销售量不低于24 kg 的时间段为“最佳销售期”,则此次销售过程中“最佳销 售期”共有多少天 在此期间销售单价最高为多少元
23.如图,直线l :y=kx+1 与 x 轴交于点D,直线l :y=-x+b 与 x 轴交于点A,且经过定点 B(-1,5), 直线l 与 l 交于点C(2,m).
(1)填空:k= ;b= ;m=
(2)在x 轴上是否存在一点E,使△BCE 的周长最短 若存在,请求出点E 的坐标;若 不存在,请说明理由.
(3)若动点P 在射线 DC上从点D 开始以每秒1个单位长度的速度运动,连接AP, 设 点 P 的运动时间为ts.当△ACP 和△ADP 的面积比为1:3时,求t的值.
第十九章检测卷
1.B 2.D 3.D 4.B 5.C 6.D 7.D 8.C 9.C
10.C 11.x≤2且 x≠-3 12.y=3x-513.914.-315.y=-2x-2
16.解:(1)∵关于x 的函数y=(m-1)x-(3m+1)是正比例函数,
∴3m+1=0,m-1≠0.
解得
(2)∵y 随x 的增大而减小, ∴m-1<0.
∴m<1.
17.解:(1)放水时间
(2)624
设 Q 与 t 的关系式为Q=kt+b.
将t=0,Q=936 和 t=1,Q=858代入,
得 解得
∴Q 与 t 的关系式为Q=-78t+936.
(3)当Q=0 时,得-78t+936=0, 解得t=12. ∴放完游泳池里的水共需要12 h.
18. 解:(1)x=-1 x>2
(2)根据图象可以得到关于x 的不等式组的 解集是-1(3)∵点C(1,3),
∴由图象可知,不等式k x+b >kx+b 的解集是x>1.
19.解:(1)5 -1
(2)函数的图象如图所示
(3)①③
(4)-1≤x≤3
20.解:(1)20 140
(2)设线段AB的解析式为y=kx+b(O≤x≤4). 将点(0,20)和(4,140)代入,
解得
∴y=30x+20(O≤x≤4).
设线段DE 的解析式为y=mx+n(O≤x≤6).
将点(0,120)和(6,0)代入,
得 解得
∴y=-20x+120(O≤x≤6).
令30x+20=-20x+120, 解得x=2.
∴注水2min时,甲、乙两个容器中水的深度相同.
21. 解:(1)设y1=k1x+80.
把点(1,95)代入,得 k1+80=95.
解得k1=15.
∴y1=15x+80(x≥0).
设 y2=k2x.
把点(1,30)代入,得k2=30.
∴y2=30x(x≥0).
(2)当y =y 时,15x+80=30x. 解得
当 y >y 时,15x+80>30x.解得
当y∴当租车时间头h, 选择甲、乙公司一样合算;当租车时间小于,选择乙公司合算;当租车时间大于 选择甲公司合算.
22.解:
(2)设销售单价p(元/kg) 与销售时间x(天)之间的函 数解析式为p=mx+n(10≤x≤20).
∵点(10,10),(20,8)在p=mx+n 的图象上,
解得
当x=10 时,p=10,y=20,
销售金额为10×20=200(元). 当 x=15 时,p=9,y=30,
销售金额为9×30=270(元).
故第10天和第15天的销售金额分别为200元,270元.
(3)若日销售量不低于24 kg,则y≥24.
当0≤x≤15 时,2x≥24,得x≥12.
当15∴“最佳销售期”共有5天.
∴p 随 x 的增大而减小.
∴ 当x=12 时,p 有最大值,P最大=9.6.
答:此次销售过程中“最佳销售期”共有5天,在此期间 销售单价最高为9.6元/kg.
23.解
(2)如图,作点C 关于x 轴的对称点C′,连接BC '交x 轴 于点E, 连接EC, 则此时△BCE 的周长最小.
∵C(2,2), ∴C'(2,-2).
设直线BC'的解析式为y=mx+n. 把 B(-1,5),C'(2,-2) 代人,
得解得
∴直线BC′的解析式 令 y=0, 得
∴存在点1 ,使△BCE的周长最短.
(3)∵直线, ∴D(-2,0). ∵C(2,2),∴CD=
∵ 点P 的运动时间为ts,DP=t. 分两种情况:
①当点P 在线段DC 上时,如图.
∵△ACP和△ADP的面积比为1:3,
②当点P 在线段DC 的延长线上时,如图. ∵△ACP和△ADP的面积比为1:3,
∴t=3√5.
综上所述,当△ACP 和△ADP的面积比为1:3时,t 的值为或
(满分:120分 时间:120分钟)
题 号 一 二 三 四 五 总 分
得 分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.在圆周长的计算公式C=2πr 中,变量有 ( ) A.C,π B.C,r C.π,r D.2π,r
2.若正比例函数y=kx 的图象经过点(-2,3),则 k 的值为 ( )
B D
3.若点A(-5,y ) 和 B(-3,y ) 都在直线y=-3x+2 上,则y 与y 的关系是 ( ) A.y ≤y B.y =y C.y
4.将一次函数y=2x 的图象沿y 轴向上平移5个单位长度,所得直线的解析式为( ) A.y=2x-5 B.y=2x+5 C.y=2x+8 D.y=2x-8
5.关于函数y=-2x+1, 下列结论正确的是 ( )
A.图象必经过点(-2,1) B.图象经过第一、二、三象限
C. 当 时 ,y<0 D.y 随x 的增大而增大
6.如图所示,函数y =ax+b 和y =|x| 的图象相交于(-1,1),(2,2)两点.当y >y 时 ,x 的取值范围是 ( )
A.x<-1 B.-1
7.如果一次函数y=kx+k+1的图象经过第一、二、四象限,则 k 的取值范围是 ( ) A.k>-1 B.k<-1 C.k<0 D.-1
A.(0,1) B.(1,2) C.(2,1) D.(3,0)
9.一次函数y=ax+b 与y=bx+a 的图象在同一坐标系内的大致位置有可能是 ( )
A
B
C
D
10.甲、乙两只气球分别从不同高度同时匀速上升60 min,气球所在位置距离地面的高度 y(单位:m) 与气球上升的时间x(单位:min)之间的函数关系如图所示.下列说法正确的是 ( )
A.甲气球上升过程中y 与 x 的函数关系式为y=2x+5 B.10min 时,甲气球在乙气球上方
C. 两气球高度差为15m 时,上升时间为50 min
D.上升60min 时,乙气球距离地面的高度为40m
二、填空题:本大题共5小题,每小题3分,共15分.
11.函数中,自变量x 的取值范围是
12.直线y=kx+b 平行于直线y=3x, 且过点(1,-2),则其解析式为
13.中国茶文化博大精深,祁门红茶在国内外享有盛誉,并被评为“中华十大名茶”.泡茶 时,水温很有讲究.祁门红茶的冲泡温度一般建议在90℃~95℃,为了冲泡出来的茶 口感更佳,徽徽同学在煮茶时记录了水温 T(单位:℃)随时间 t(单位:min)变化的数 据,如下表.若水温的变化是均匀的,则水温达到90℃的时间是 min.
时间t/min 0 2 4 6
水温T/℃ 18 34 50 66
14.如图,在平面直角坐标系中,正方形ABCD 的边长为3,点A 的坐标为(1,1).若直线 y=x+b 与正方形有两个公共点,则b 的取值范围是
第14题图 第15题图
15.如图,已知一条直线经过点A(0,2) 、 点 B(1,0),将这条直线平移后与x 轴、y 轴分别
交于点 C、点 D.若 DB=DC, 则直线 CD的函数解析式为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.已知关于x 的函数y=(m-1)x-(3m+1).
(1)若函数为正比例函数,求m 的值;
(2)若y 随 x 的增大而减小,求 m 的取值范围.
17.游泳池应定期换水,某游泳池在一次换水前存水936 m ,换水时关闭进水孔打开排水孔,当放水时间增加时,游泳池的存水随之减少.设放水时间为th, 游泳池的存水量为 Qm , 它们的变化情况如表:
放水时间t/h 0 1 2 3 4 5
游泳池的存水量Q/m 936 858 780 702 a 546
(1)在这个变化过程中,自变量是
(2)上述表格中,a= ,并写出 Q 与 t的关系式.
(3)放完游泳池里的水共需要多长时间
18.在学习一元一次不等式与一次函数中,小明在同一个坐标系中分别作出了一次函数 y=k1x+b 和 y=kx+b 的图象,分别与x 轴交于点A,B, 两直线交于点C. 已知点A(-1, 0),B(2,0), 观察图象并回答下列问题:
(1)关于x 的方程k1x+b1=0 的解是 ;关于x 的不等式 kx+b<0 的解集是 ;
(2)直接写出关于x 的不等式 的解集;
(3)若点C(1,3), 求关于x 的不等式k1x+b1>x+b 的解集.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.本学期,我们学习了“ 一元一次不等式与一次函数”,请利用所学知识来解决下面的问题:在函数y=2|x-1|-1中,下表是y 与x 的几组对应值.
x … -3 -2 -1 0 1 2 3 …
y … 7 m 3 1 n 1 3 …
(1)m= ,n=
(2)在下面给出的平面直角坐标系中,画出这个函数的图象.
(3)根据图象,下列关于该函数性质的说法中正确的是 . (填序号)
①该函数图象是轴对称图形,对称轴为直线x=1;
②当x<1 时,y 随x 的增大而增大,当x≥1 时 ,y随x 的增大而减小;
③该函数在自变量的取值范围内有最小值,当x=1 时有最小值-1.
(4)根据图象,直接写出不等式2|x-1|-1≤3 的解集:
20.如图,水平放置的甲容器内原有120 mm 高的水,乙容器中有一圆柱形实心铁块立放其中(圆柱形铁块的下底面完全落在乙容器底面上).现将甲容器中的水匀速注入乙容器,且乙容器中水不外溢.甲、乙两个容器中水的深度y(mm) 与注水时间x(min) 之间的关系如图 .
(1)乙容器中原有水的高度是 mm,铁块的高度是 mm;
(2)注水多长时间时,甲、乙两个容器中水的深度相同
21.“五 ·一”期间,小明一家乘坐高铁前往某市旅游,计划第二天租用新能源汽车自驾出游.甲公司收费:按日收取固定租金80元,另外再按出租时间计费;乙公司收费:无固定租金,直接以租车时间计费,每小时的租金是30元.
(1)设租车时间为xh, 租用甲公司的车所需费用为y 元,租用乙公司的车所需费用 为y 元,分别求出y ,y 关于x 的函数解析式;
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,某个体户购进一批时令水果,20天销售完毕.他将本次销售情况进行了跟踪记 录,并根据所记录的数据绘制函数图象,其中日销售量y(kg) 与销售时间x(天)之间 的函数关系如图①所示,销售单价p(元/kg)与销售时间x(天)之间的部分函数关系 如图②所示.
(1)直接写出y 与x 之间的函数关系式.
(2)分别求出第10天和第15天的销售金额.
(3)若日销售量不低于24 kg 的时间段为“最佳销售期”,则此次销售过程中“最佳销 售期”共有多少天 在此期间销售单价最高为多少元
23.如图,直线l :y=kx+1 与 x 轴交于点D,直线l :y=-x+b 与 x 轴交于点A,且经过定点 B(-1,5), 直线l 与 l 交于点C(2,m).
(1)填空:k= ;b= ;m=
(2)在x 轴上是否存在一点E,使△BCE 的周长最短 若存在,请求出点E 的坐标;若 不存在,请说明理由.
(3)若动点P 在射线 DC上从点D 开始以每秒1个单位长度的速度运动,连接AP, 设 点 P 的运动时间为ts.当△ACP 和△ADP 的面积比为1:3时,求t的值.
第十九章检测卷
1.B 2.D 3.D 4.B 5.C 6.D 7.D 8.C 9.C
10.C 11.x≤2且 x≠-3 12.y=3x-513.914.-3
16.解:(1)∵关于x 的函数y=(m-1)x-(3m+1)是正比例函数,
∴3m+1=0,m-1≠0.
解得
(2)∵y 随x 的增大而减小, ∴m-1<0.
∴m<1.
17.解:(1)放水时间
(2)624
设 Q 与 t 的关系式为Q=kt+b.
将t=0,Q=936 和 t=1,Q=858代入,
得 解得
∴Q 与 t 的关系式为Q=-78t+936.
(3)当Q=0 时,得-78t+936=0, 解得t=12. ∴放完游泳池里的水共需要12 h.
18. 解:(1)x=-1 x>2
(2)根据图象可以得到关于x 的不等式组的 解集是-1
∴由图象可知,不等式k x+b >kx+b 的解集是x>1.
19.解:(1)5 -1
(2)函数的图象如图所示
(3)①③
(4)-1≤x≤3
20.解:(1)20 140
(2)设线段AB的解析式为y=kx+b(O≤x≤4). 将点(0,20)和(4,140)代入,
解得
∴y=30x+20(O≤x≤4).
设线段DE 的解析式为y=mx+n(O≤x≤6).
将点(0,120)和(6,0)代入,
得 解得
∴y=-20x+120(O≤x≤6).
令30x+20=-20x+120, 解得x=2.
∴注水2min时,甲、乙两个容器中水的深度相同.
21. 解:(1)设y1=k1x+80.
把点(1,95)代入,得 k1+80=95.
解得k1=15.
∴y1=15x+80(x≥0).
设 y2=k2x.
把点(1,30)代入,得k2=30.
∴y2=30x(x≥0).
(2)当y =y 时,15x+80=30x. 解得
当 y >y 时,15x+80>30x.解得
当y
22.解:
(2)设销售单价p(元/kg) 与销售时间x(天)之间的函 数解析式为p=mx+n(10≤x≤20).
∵点(10,10),(20,8)在p=mx+n 的图象上,
解得
当x=10 时,p=10,y=20,
销售金额为10×20=200(元). 当 x=15 时,p=9,y=30,
销售金额为9×30=270(元).
故第10天和第15天的销售金额分别为200元,270元.
(3)若日销售量不低于24 kg,则y≥24.
当0≤x≤15 时,2x≥24,得x≥12.
当15
∴p 随 x 的增大而减小.
∴ 当x=12 时,p 有最大值,P最大=9.6.
答:此次销售过程中“最佳销售期”共有5天,在此期间 销售单价最高为9.6元/kg.
23.解
(2)如图,作点C 关于x 轴的对称点C′,连接BC '交x 轴 于点E, 连接EC, 则此时△BCE 的周长最小.
∵C(2,2), ∴C'(2,-2).
设直线BC'的解析式为y=mx+n. 把 B(-1,5),C'(2,-2) 代人,
得解得
∴直线BC′的解析式 令 y=0, 得
∴存在点1 ,使△BCE的周长最短.
(3)∵直线, ∴D(-2,0). ∵C(2,2),∴CD=
∵ 点P 的运动时间为ts,DP=t. 分两种情况:
①当点P 在线段DC 上时,如图.
∵△ACP和△ADP的面积比为1:3,
②当点P 在线段DC 的延长线上时,如图. ∵△ACP和△ADP的面积比为1:3,
∴t=3√5.
综上所述,当△ACP 和△ADP的面积比为1:3时,t 的值为或
