1.1.2 图形的构成 课件(共35张PPT)
文档属性
| 名称 | 1.1.2 图形的构成 课件(共35张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 5.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 22:02:43 | ||
图片预览









文档简介
(共35张PPT)
1.1.2 图形的构成
第一章 丰富的图形世界
北师大2024版数学七年级上册【示范课精品课】
授课教师:********
班 级:********
时 间:********
学习目标
1. 通过丰富的实例,进一步认识点、线、面、体,初步感受点、线、面、体之间的关系。
2.经历从现实世界中抽象出几何图形的过程,从构成图形的基本元素的角度进一步认识常见几何体的特征;通过大量的实例,经历观察、分析、抽象、概括、操作等实践活动,进一步发展学生的空间观念。
展示一段包含各种建筑、生活用品、自然景观等的视频,其中突出展示各种丰富多样的图形元素,如建筑物中的正方体、圆柱形状的柱子,生活中的球体篮球、长方体的盒子,自然界中的圆形的花朵、三角形的山峰等。
提问学生:“在这段视频中,你们都看到了哪些不同形状的物体?这些物体的形状可以如何分类呢?” 引导学生观察并思考,从而引出本节课的主题 —— 丰富的图形世界。
让学生分享自己在生活中还见过哪些独特的图形,激发学生对图形的兴趣和好奇心。
(二)认识立体图形(10 分钟)
展示正方体、长方体、圆柱、圆锥、球等常见立体图形的实物模型和图片。
分别介绍每种立体图形的名称,并引导学生观察它们的特征,从面的形状、数量,棱的数量、长度关系,顶点的数量等方面进行描述。
正方体:有 6 个完全相同的正方形面,12 条棱长度都相等,8 个顶点。
长方体:有 6 个面,相对的面完全相同,一般情况下 6 个面都是长方形(特殊情况有两个相对的面是正方形),12 条棱,相对的棱长度相等,8 个顶点。
圆柱:有两个底面,是完全相同的圆,侧面是一个曲面,展开后是一个长方形。
圆锥:有一个底面,是一个圆,侧面是一个曲面,展开后是一个扇形,有一个顶点。
球:由一个曲面围成,球面上任意一点到球心的距离都相等。
组织学生分组,通过触摸、观察手中的立体图形模型,再次加深对各种立体图形特征的认识,并让小组代表发言,描述自己所观察图形的特征。
进行小游戏 “我说你猜”,教师描述一个立体图形的特征,让学生快速猜出对应的立体图形名称,巩固学生对立体图形特征的记忆。
(三)立体图形的展开图(10 分钟)
拿出一个正方体纸盒,沿着棱将其剪开,展示正方体的展开图。
让学生观察展开图的形状,思考正方体展开图有哪些不同的形式。
组织学生分组,用准备好的正方体纸盒进行展开操作,尝试找出尽可能多的不同展开图形式,并将其绘制在纸上。
每个小组展示自己找到的正方体展开图形式,全班共同总结正方体展开图的常见类型(如 “1 - 4 - 1” 型、“2 - 3 - 1” 型、“2 - 2 - 2” 型、“3 - 3” 型等)。
展示圆柱、圆锥的展开图图片,让学生观察并理解圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形,底面都是圆。
布置任务:让学生课后自己动手制作圆柱和圆锥的展开图,并尝试将展开图还原成对应的立体图形,加深对立体图形展开图的理解。
(四)点、线、面、体(10 分钟)
展示一些生活中的实例图片,如流星划过夜空留下的光线(点动成线)、汽车雨刮器在挡风玻璃上扫过的痕迹(线动成面)、旋转门的转动(面动成体)等,引导学生观察并思考点、线、面、体之间的关系。
讲解点、线、面、体的基本概念:
点:是构成图形的基本元素,没有大小和形状。
线:可以分为直线和曲线,线由点组成,线有长短,没有粗细。
面:分为平面和曲面,面由线组成,面有大小,没有厚度。
体:由面围成,占有一定的空间。
组织学生进行小组讨论,举例说明生活中还有哪些点动成线、线动成面、面动成体的现象。
利用多媒体动画演示点、线、面、体之间的动态转化过程,如一个点运动形成一条直线,一条直线绕着一个端点旋转形成一个平面,一个长方形绕着一条边旋转形成一个圆柱等,让学生更直观地感受它们之间的关系。
(五)从不同方向看(15 分钟)
展示一个由若干个小正方体组成的简单立体图形,提问学生:“从不同的方向看这个物体,我们会看到怎样的图形呢?” 引发学生的思考。
介绍从不同方向观察物体的三个主要视角:
主视图:从正面看到的图形。
俯视图:从上面看到的图形。
左视图:从左面看到的图形。
教师在讲台上摆放一个简单的物体(如一个由 3 个小正方体组成的 “L” 型结构),让学生分别从正面、上面、左面进行观察,并请几位学生上台在黑板上画出他们所看到的图形。
教师对学生画出的图形进行点评,纠正错误,强调在画三视图时要注意图形的形状、位置和大小关系,以及看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示。
给出一些简单的立体图形(如正方体、长方体、圆柱、圆锥等的组合体),让学生在练习本上画出它们的三视图,教师巡视指导,及时发现并解决学生在画图过程中出现的问题。
展示一些物体的三视图,让学生尝试根据三视图想象出物体的形状,并在小组内交流讨论,然后用小正方体搭建出对应的物体,验证自己的想象是否正确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
立体图形的构成
探究新知
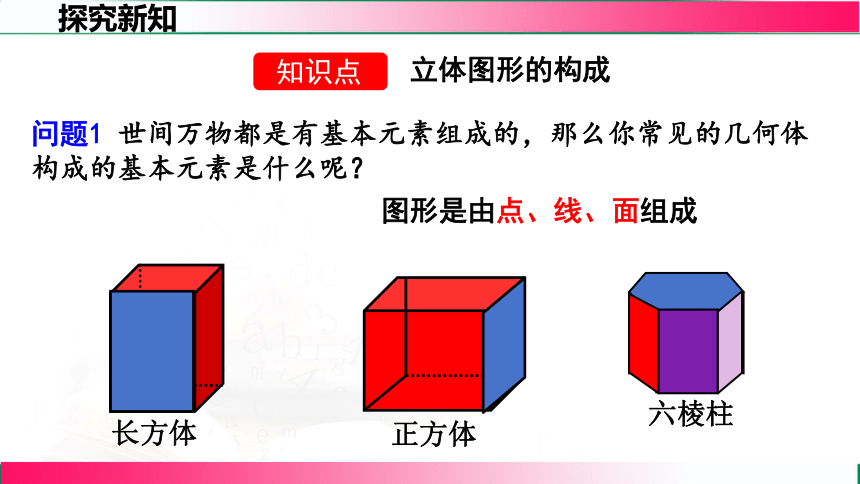
正方体
六棱柱
图形是由点、线、面组成
长方体
问题1 世间万物都是有基本元素组成的,那么你常见的几何体构成的基本元素是什么呢?
探究新知
点
探究新知
线:直线和曲线
探究新知
平面
曲面
面
探究新知
曲面
平面
探究新知
面与面相交的地方形成线
探究新知
面与面相交的地方形成线
线与线相交的地方为点
探究新知
探究新知
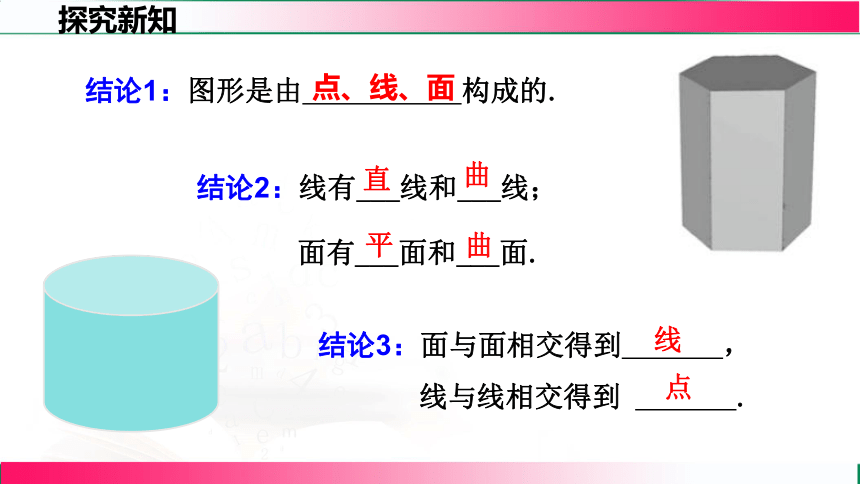
结论3:面与面相交得到 ,
线与线相交得到 .
结论2:线有___线和___线;
面有___面和___面.
平
曲
直
曲
线
点
结论1:图形是由 构成的.
点、线、面
探究新知
问题2 你发现点线面与几何体之间有什么关系?
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
点动成线
探究新知
线动成面
探究新知
线动成面
探究新知
三角形绕一边旋转成圆锥体
面动成体
探究新知
长方形绕一边旋转成圆柱体
面动成体
探究新知
点线面在运动过程中与几何体的关系:
结论4:
点动成线
线动成面
面动成体
点是构成图形的基本元素
几何图形是由点、线、面、体组成的
探究新知
练一练
线动成
面动成
线
面
体
点动成
探究新知
练一练 图中各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到?用线连一连.
例1 指出下图的立体图形中各有几个面,是平的还是曲的,各有几个顶点,棱的条数?
探究新知
素养考点 1
立体图形的组成元素
长方体有6个面,都是平的;有8个顶点,有12条棱.
长方体
圆柱
圆柱有3个面,上、下底面是平的,侧面是曲的;没有顶点,没有棱.
方法点拨:在立体图形中,面与面相交得到线,线与线相交得到点.在数面时可先数底面,再数侧面;数棱时,可先数底面与侧面相交的棱,再数侧面与侧面相交的棱;根据棱与棱相交得到的点是顶点来确定顶点个数.
素养考点 3
立体图形的计算
探究新知
例3 已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面 一共有多少条棱 这些棱的长度之和是多少
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少
探究新知
这些棱的长度之和为 6×8+(18-6)×5=108厘米;
(2)将其侧面沿一条棱展开,展开图是一个长方形,长为5×6=30厘米,宽是6厘米,因而面积是30×8=240(平方厘米).
方法点拨:解决本题的关键是理解棱柱的构造特点,(1)n棱柱有n+2个面,3n条棱,据此求解;
(2)侧面展开图为长方形,求出长为5×6=30厘米,宽是6厘米,即可求出面积.
解:(1)这个六棱柱一共有6+2=8个面,一共有6×3=18条棱;其中侧棱的长度都是8厘米,其他棱长都为底面边长5厘米;
1. [2024益阳期末]下图所示的4个几何体中,由5个面围成的
是( D )
D
1
2
3
4
5
6
7
2. [母题·教材P5随堂练习T1]如图,上排的平面图形绕虚线
旋转一周,可以得到下排的立体图形,那么与甲、乙、
丙、丁各平面图形顺序对应的立体图形的编号应为
( A )
A. ③④①②
B. ①②③④
C. ③②④①
D. ④③②①
A
1
2
3
4
5
6
7
3. 一个棱柱有7个面,则它的顶点数是 .
【点拨】
n 棱柱有2 n 个顶点,3 n 条棱,( n +2)个面.一个棱
柱的面数为7,则这个棱柱是五棱柱,顶点数为10.
10
1
2
3
4
5
6
7
4. [2024烟台期中]如图所示的几何体中,面与面相交形成的
线共有 条.
9
1
2
3
4
5
6
7
5. [2024十堰模拟]观察下图,把左边的图形绕着给定的虚线
旋转一周后可能形成的立体图形是( D )
D
1
2
3
4
5
6
7
6. [情境题·生活应用·2024·东营期末]小丽跟妈妈到银行办理
业务,她发现银行大堂的旋转门内部是由三块宽为2 m、
高为3 m的玻璃隔板组成的.此情此景,让她想起了七年
级数学第一章《丰富的图形世界》里的知识,她提出了以
下问题,你能帮她解决吗?
(1)将此旋转门旋转一周,能形成的几何体是 .
圆柱
1
2
3
4
5
6
7
(2)这能说明的事实是( C )
A. 点动成线 B. 线动成面
C. 面动成体
(3)求该旋转门旋转一周形成的几何体的体积.(边框及衔接
处忽略不计,结果保留π)
【解】π×22×3=12π(m3),故该旋转门旋转一周形成
的几何体的体积是12π m3.
C
1
2
3
4
5
6
7
7. [母题·教材P21复习题T12]探究:有一个长为6 cm,宽为4
cm的长方形纸板,现要求以其一组对边中点所在直线为
轴,旋转180°,得到一个圆柱.现可按照两种方案进行操
作:方案一:以较长的一组对边中点所在直线为轴旋转,
如图①;方案二:以较短的一组对边中点所在直线为轴旋
转,如图②.
1
2
3
4
5
6
7
(1)请判断哪种方案构造的圆柱体积大;
【解】方案一:旋转半径 r = ×6=3(cm),所以体积
为π r2 h =π×32×4=36π(cm3);
方案二:旋转半径 r = ×4=2(cm),
所以体积为π r2 h =π×22×6=24π(cm3).
因为36 π>24 π,所以方案一构造的圆柱体积大.
1
2
3
4
5
6
7
教材习题:完成教材6-7页习题1.1的3,7,8,9题。
实践性作业:在家中找一几何体,想一想它可以由什么样的平面图形旋转得到,并描述其结构特征。
谢谢观看!
1.1.2 图形的构成
第一章 丰富的图形世界
北师大2024版数学七年级上册【示范课精品课】
授课教师:********
班 级:********
时 间:********
学习目标
1. 通过丰富的实例,进一步认识点、线、面、体,初步感受点、线、面、体之间的关系。
2.经历从现实世界中抽象出几何图形的过程,从构成图形的基本元素的角度进一步认识常见几何体的特征;通过大量的实例,经历观察、分析、抽象、概括、操作等实践活动,进一步发展学生的空间观念。
展示一段包含各种建筑、生活用品、自然景观等的视频,其中突出展示各种丰富多样的图形元素,如建筑物中的正方体、圆柱形状的柱子,生活中的球体篮球、长方体的盒子,自然界中的圆形的花朵、三角形的山峰等。
提问学生:“在这段视频中,你们都看到了哪些不同形状的物体?这些物体的形状可以如何分类呢?” 引导学生观察并思考,从而引出本节课的主题 —— 丰富的图形世界。
让学生分享自己在生活中还见过哪些独特的图形,激发学生对图形的兴趣和好奇心。
(二)认识立体图形(10 分钟)
展示正方体、长方体、圆柱、圆锥、球等常见立体图形的实物模型和图片。
分别介绍每种立体图形的名称,并引导学生观察它们的特征,从面的形状、数量,棱的数量、长度关系,顶点的数量等方面进行描述。
正方体:有 6 个完全相同的正方形面,12 条棱长度都相等,8 个顶点。
长方体:有 6 个面,相对的面完全相同,一般情况下 6 个面都是长方形(特殊情况有两个相对的面是正方形),12 条棱,相对的棱长度相等,8 个顶点。
圆柱:有两个底面,是完全相同的圆,侧面是一个曲面,展开后是一个长方形。
圆锥:有一个底面,是一个圆,侧面是一个曲面,展开后是一个扇形,有一个顶点。
球:由一个曲面围成,球面上任意一点到球心的距离都相等。
组织学生分组,通过触摸、观察手中的立体图形模型,再次加深对各种立体图形特征的认识,并让小组代表发言,描述自己所观察图形的特征。
进行小游戏 “我说你猜”,教师描述一个立体图形的特征,让学生快速猜出对应的立体图形名称,巩固学生对立体图形特征的记忆。
(三)立体图形的展开图(10 分钟)
拿出一个正方体纸盒,沿着棱将其剪开,展示正方体的展开图。
让学生观察展开图的形状,思考正方体展开图有哪些不同的形式。
组织学生分组,用准备好的正方体纸盒进行展开操作,尝试找出尽可能多的不同展开图形式,并将其绘制在纸上。
每个小组展示自己找到的正方体展开图形式,全班共同总结正方体展开图的常见类型(如 “1 - 4 - 1” 型、“2 - 3 - 1” 型、“2 - 2 - 2” 型、“3 - 3” 型等)。
展示圆柱、圆锥的展开图图片,让学生观察并理解圆柱的侧面展开图是长方形,圆锥的侧面展开图是扇形,底面都是圆。
布置任务:让学生课后自己动手制作圆柱和圆锥的展开图,并尝试将展开图还原成对应的立体图形,加深对立体图形展开图的理解。
(四)点、线、面、体(10 分钟)
展示一些生活中的实例图片,如流星划过夜空留下的光线(点动成线)、汽车雨刮器在挡风玻璃上扫过的痕迹(线动成面)、旋转门的转动(面动成体)等,引导学生观察并思考点、线、面、体之间的关系。
讲解点、线、面、体的基本概念:
点:是构成图形的基本元素,没有大小和形状。
线:可以分为直线和曲线,线由点组成,线有长短,没有粗细。
面:分为平面和曲面,面由线组成,面有大小,没有厚度。
体:由面围成,占有一定的空间。
组织学生进行小组讨论,举例说明生活中还有哪些点动成线、线动成面、面动成体的现象。
利用多媒体动画演示点、线、面、体之间的动态转化过程,如一个点运动形成一条直线,一条直线绕着一个端点旋转形成一个平面,一个长方形绕着一条边旋转形成一个圆柱等,让学生更直观地感受它们之间的关系。
(五)从不同方向看(15 分钟)
展示一个由若干个小正方体组成的简单立体图形,提问学生:“从不同的方向看这个物体,我们会看到怎样的图形呢?” 引发学生的思考。
介绍从不同方向观察物体的三个主要视角:
主视图:从正面看到的图形。
俯视图:从上面看到的图形。
左视图:从左面看到的图形。
教师在讲台上摆放一个简单的物体(如一个由 3 个小正方体组成的 “L” 型结构),让学生分别从正面、上面、左面进行观察,并请几位学生上台在黑板上画出他们所看到的图形。
教师对学生画出的图形进行点评,纠正错误,强调在画三视图时要注意图形的形状、位置和大小关系,以及看得见的轮廓线用实线表示,看不见的轮廓线用虚线表示。
给出一些简单的立体图形(如正方体、长方体、圆柱、圆锥等的组合体),让学生在练习本上画出它们的三视图,教师巡视指导,及时发现并解决学生在画图过程中出现的问题。
展示一些物体的三视图,让学生尝试根据三视图想象出物体的形状,并在小组内交流讨论,然后用小正方体搭建出对应的物体,验证自己的想象是否正确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
知识点
立体图形的构成
探究新知
正方体
六棱柱
图形是由点、线、面组成
长方体
问题1 世间万物都是有基本元素组成的,那么你常见的几何体构成的基本元素是什么呢?
探究新知
点
探究新知
线:直线和曲线
探究新知
平面
曲面
面
探究新知
曲面
平面
探究新知
面与面相交的地方形成线
探究新知
面与面相交的地方形成线
线与线相交的地方为点
探究新知
探究新知
结论3:面与面相交得到 ,
线与线相交得到 .
结论2:线有___线和___线;
面有___面和___面.
平
曲
直
曲
线
点
结论1:图形是由 构成的.
点、线、面
探究新知
问题2 你发现点线面与几何体之间有什么关系?
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
·
点动成线
探究新知
线动成面
探究新知
线动成面
探究新知
三角形绕一边旋转成圆锥体
面动成体
探究新知
长方形绕一边旋转成圆柱体
面动成体
探究新知
点线面在运动过程中与几何体的关系:
结论4:
点动成线
线动成面
面动成体
点是构成图形的基本元素
几何图形是由点、线、面、体组成的
探究新知
练一练
线动成
面动成
线
面
体
点动成
探究新知
练一练 图中各个花瓶的表面可以看做由哪个平面图形绕虚线旋转一周而得到?用线连一连.
例1 指出下图的立体图形中各有几个面,是平的还是曲的,各有几个顶点,棱的条数?
探究新知
素养考点 1
立体图形的组成元素
长方体有6个面,都是平的;有8个顶点,有12条棱.
长方体
圆柱
圆柱有3个面,上、下底面是平的,侧面是曲的;没有顶点,没有棱.
方法点拨:在立体图形中,面与面相交得到线,线与线相交得到点.在数面时可先数底面,再数侧面;数棱时,可先数底面与侧面相交的棱,再数侧面与侧面相交的棱;根据棱与棱相交得到的点是顶点来确定顶点个数.
素养考点 3
立体图形的计算
探究新知
例3 已知一个六棱柱,它的底面边长都是5厘米,侧棱长都是8厘米,请回答下列问题
(1)这个六棱柱一共有多少个面 一共有多少条棱 这些棱的长度之和是多少
(2)沿一条侧棱将这个六棱柱侧面全部展开成一个平面图形,这个图形的面积是多少
探究新知
这些棱的长度之和为 6×8+(18-6)×5=108厘米;
(2)将其侧面沿一条棱展开,展开图是一个长方形,长为5×6=30厘米,宽是6厘米,因而面积是30×8=240(平方厘米).
方法点拨:解决本题的关键是理解棱柱的构造特点,(1)n棱柱有n+2个面,3n条棱,据此求解;
(2)侧面展开图为长方形,求出长为5×6=30厘米,宽是6厘米,即可求出面积.
解:(1)这个六棱柱一共有6+2=8个面,一共有6×3=18条棱;其中侧棱的长度都是8厘米,其他棱长都为底面边长5厘米;
1. [2024益阳期末]下图所示的4个几何体中,由5个面围成的
是( D )
D
1
2
3
4
5
6
7
2. [母题·教材P5随堂练习T1]如图,上排的平面图形绕虚线
旋转一周,可以得到下排的立体图形,那么与甲、乙、
丙、丁各平面图形顺序对应的立体图形的编号应为
( A )
A. ③④①②
B. ①②③④
C. ③②④①
D. ④③②①
A
1
2
3
4
5
6
7
3. 一个棱柱有7个面,则它的顶点数是 .
【点拨】
n 棱柱有2 n 个顶点,3 n 条棱,( n +2)个面.一个棱
柱的面数为7,则这个棱柱是五棱柱,顶点数为10.
10
1
2
3
4
5
6
7
4. [2024烟台期中]如图所示的几何体中,面与面相交形成的
线共有 条.
9
1
2
3
4
5
6
7
5. [2024十堰模拟]观察下图,把左边的图形绕着给定的虚线
旋转一周后可能形成的立体图形是( D )
D
1
2
3
4
5
6
7
6. [情境题·生活应用·2024·东营期末]小丽跟妈妈到银行办理
业务,她发现银行大堂的旋转门内部是由三块宽为2 m、
高为3 m的玻璃隔板组成的.此情此景,让她想起了七年
级数学第一章《丰富的图形世界》里的知识,她提出了以
下问题,你能帮她解决吗?
(1)将此旋转门旋转一周,能形成的几何体是 .
圆柱
1
2
3
4
5
6
7
(2)这能说明的事实是( C )
A. 点动成线 B. 线动成面
C. 面动成体
(3)求该旋转门旋转一周形成的几何体的体积.(边框及衔接
处忽略不计,结果保留π)
【解】π×22×3=12π(m3),故该旋转门旋转一周形成
的几何体的体积是12π m3.
C
1
2
3
4
5
6
7
7. [母题·教材P21复习题T12]探究:有一个长为6 cm,宽为4
cm的长方形纸板,现要求以其一组对边中点所在直线为
轴,旋转180°,得到一个圆柱.现可按照两种方案进行操
作:方案一:以较长的一组对边中点所在直线为轴旋转,
如图①;方案二:以较短的一组对边中点所在直线为轴旋
转,如图②.
1
2
3
4
5
6
7
(1)请判断哪种方案构造的圆柱体积大;
【解】方案一:旋转半径 r = ×6=3(cm),所以体积
为π r2 h =π×32×4=36π(cm3);
方案二:旋转半径 r = ×4=2(cm),
所以体积为π r2 h =π×22×6=24π(cm3).
因为36 π>24 π,所以方案一构造的圆柱体积大.
1
2
3
4
5
6
7
教材习题:完成教材6-7页习题1.1的3,7,8,9题。
实践性作业:在家中找一几何体,想一想它可以由什么样的平面图形旋转得到,并描述其结构特征。
谢谢观看!
同课章节目录
