1.2.1 展开与折叠(第2课时) 课件(共34张PPT)
文档属性
| 名称 | 1.2.1 展开与折叠(第2课时) 课件(共34张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 22:06:09 | ||
图片预览






文档简介
(共34张PPT)
1.2.1 展开与折叠(第2课时)
第一章 丰富的图形世界
北师大2024版数学七年级上册【示范课精品课】
授课教师:********
班 级:********
时 间:********
学习目标
1.了解棱柱、圆柱、圆锥等常见几何体的表面展开图,发展几何直观.
2.能根据展开图判断和制作简单的立体图形,发展空间观念.
展示一段包含各种建筑、生活用品、自然景观等的视频,其中突出展示各种丰富多样的图形元素,如建筑物中的正方体、圆柱形状的柱子,生活中的球体篮球、长方体的盒子,自然界中的圆形的花朵、三角形的山峰等。
提问学生:“在这段视频中,你们都看到了哪些不同形状的物体?这些物体的形状可以如何分类呢?” 引导学生观察并思考,从而引出本节课的主题 —— 丰富的图形世界。
让学生分享自己在生活中还见过哪些独特的图形,激发学生对图形的兴趣和好奇心。
(二)认识立体图形(10 分钟)
展示正方体、长方体、圆柱、圆锥、球等常见立体图形的实物模型和图片。
分别介绍每种立体图形的名称,并引导学生观察它们的特征,从面的形状、数量,棱的数量、长度关系,顶点的数量等方面进行描述。
正方体:有 6 个完全相同的正方形面,12 条棱长度都相等,8 个顶点。
长方体:有 6 个面,相对的面完全相同,一般情况下 6 个面都是长方形(特殊情况有两个相对的面是正方形),12 条棱,相对的棱长度相等,8 个顶点。
圆柱:有两个底面,是完全相同的圆,侧面是一个曲面,展开后是一个长方形。
圆锥:有一个底面,是一个圆,侧面是一个曲面,展开后是一个扇形,有一个顶点。
球:由一个曲面围成,球面上任意一点到球心的距离都相等。
组织学生分想象是否正确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
课堂导入
在我们日常生活中,随处可见各种立体图形.
问题
牛奶盒、谷堆可由什么样的平面图形组成
探究新知
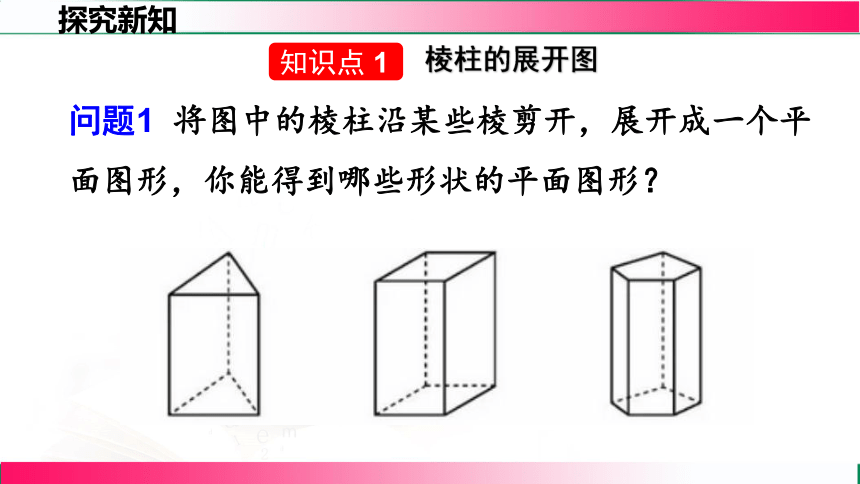
问题1 将图中的棱柱沿某些棱剪开,展开成一个平面图形,你能得到哪些形状的平面图形?
知识点 1
棱柱的展开图
探究新知
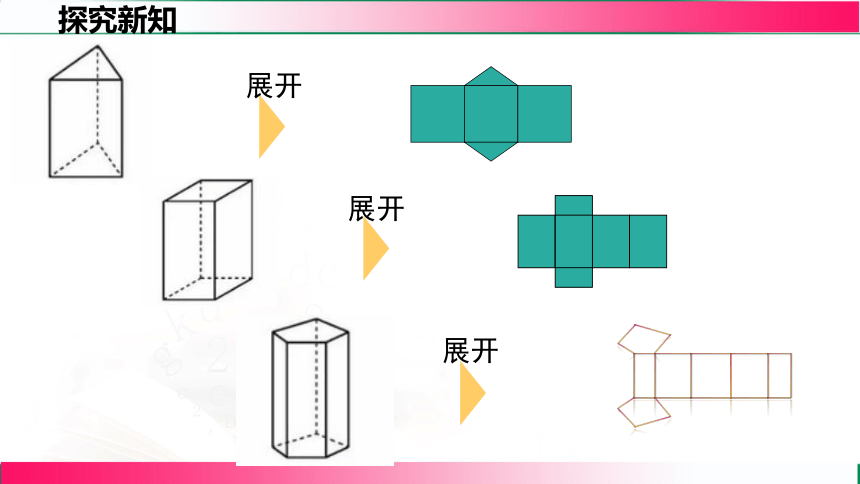
展开
展开
展开
探究新知
棱柱展开后的特征:
1.棱柱有上下两个底面,它们的形状相同.
2.棱柱侧面的形状都是平行四边形.
3.棱柱侧面的个数和底面图形的边数相等.
4.棱柱所有侧棱长都相等.
总结:
探究新知
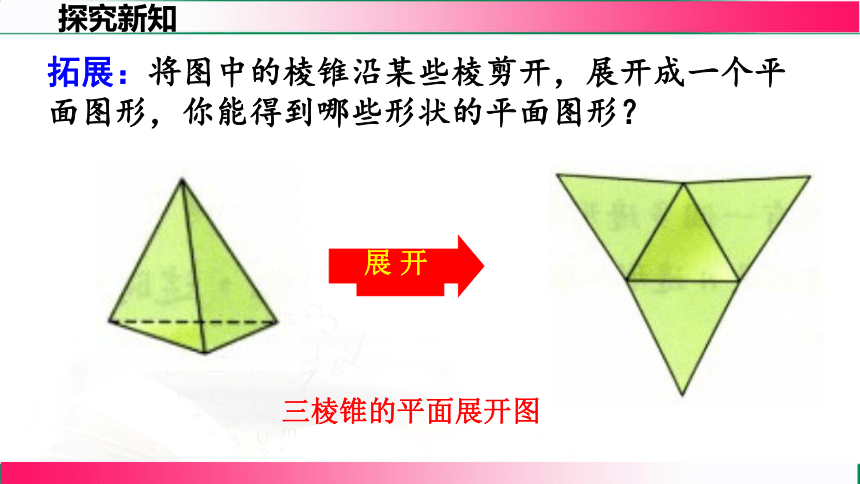
拓展:将图中的棱锥沿某些棱剪开,展开成一个平面图形,你能得到哪些形状的平面图形?
展 开
三棱锥的平面展开图
探究新知
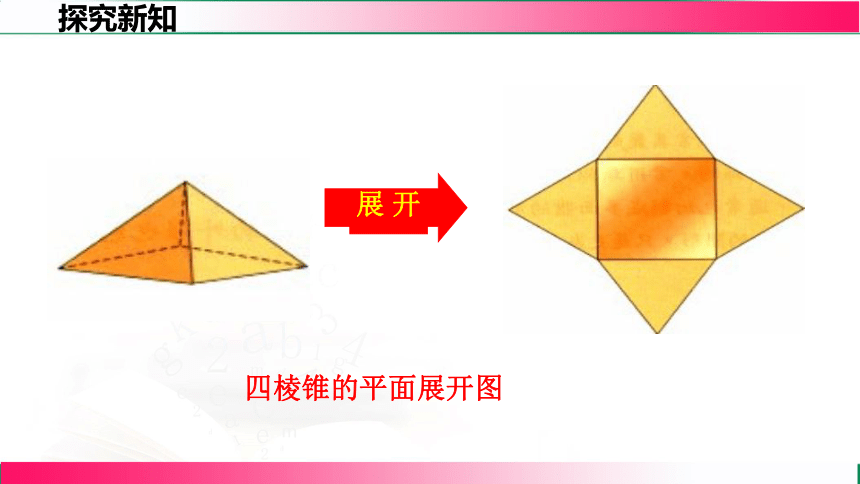
展 开
四棱锥的平面展开图
探究新知
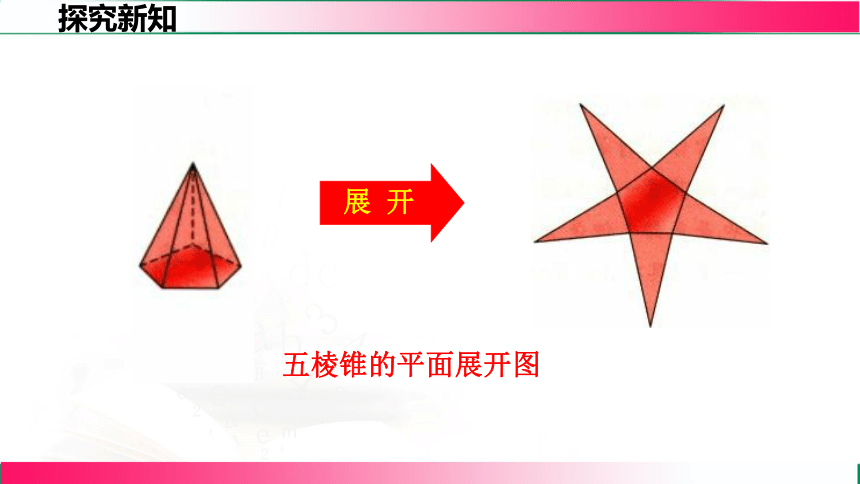
展 开
五棱锥的平面展开图
探究新知
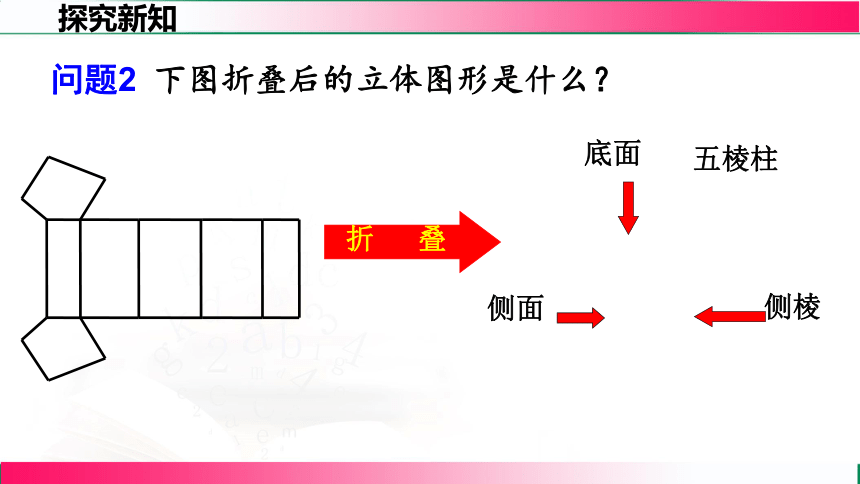
五棱柱
折 叠
底面
侧棱
侧面
问题2 下图折叠后的立体图形是什么?
探究新知
练一练 以下哪些图形经过折叠可以围成一个棱柱
⑴
⑵
⑶
⑷
探究新知
知识点 2
圆柱、圆锥的展开图
圆柱展开后的平面图形是什么样的?
思考1 圆柱侧面展开后,得到的平面图形是什么样的?
探究新知
结论:圆柱展开图是由两个等圆和一个长方形组成,其中侧面展开图的一边的长是底面圆的周长,另一边的长是圆柱的高.
思考2 圆柱展开后的平面图形是什么样的?
探究新知
圆锥展开后的平面图形是什么样的?
思考1 圆锥侧面展开后的平面图形是什么样的?
探究新知
总结:圆锥的表面展开图是由扇形和一个圆(底面)组成,其中扇形的半径是圆锥母线(即圆锥底面圆周上任一点与顶点的连线)长,而扇形的弧长则是圆锥底面圆的周长.
思考2 圆锥展开后的平面图形是什么样的?
探究新知
练一练 下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字吗?
长方体
三棱柱
圆柱
探究新知
素养考点 1
立体图形的展开与折叠
方法点拨: 由上、下底面的多边形类型可判断是几棱柱,其他类型的几何体则应记住其表面展开图的主要特征.
例1 如图是立体图形的展开图,你能说出这些立体图形的名称吗?
解:(1)长方体;(2)圆锥;(3)五棱柱;(4)三棱柱.
巩固练习
变式训练
下列图形中可以作为三棱柱的展开图的是( )
A
A.
D.
C.
B.
素养考点 2
利用表面展开图的有关数据进行计算
探究新知
例2 如图是一种食品包装盒的表面展开图.
(1)请写出这个包装盒的形状的名称:____________ .
(2)根据图中所标的尺寸,计算这个食品包装盒的表面积.
三棱柱
探究新知
解:
(2)因为AB=5,AD=3,BE=4,DF=6,
方法点拨:此题是将动手操作和计算相结合,了解立体图形表面展开图与立体图形间的关系,掌握图形面积的计算(公式)是解本题的关键.由表面展开图可知立体图形的表面积等于表面展开图各部分图形面积之和.
(1)三棱柱.
所以侧面积为3×6+5×6+4×6=18+30+24=72,
底面积为 .
所以这个食品包装盒的表面积为72+12=84.
1. [2024邢台期末]圆柱的表面展开图可能是( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
2. [母题·教材P15习题T1]如图,四个图形是由立体图形展开
得到的,相应的立体图形顺次是( A )
A. 正方体、圆柱、三棱柱、圆锥
B. 正方体、圆锥、三棱柱、圆柱
C. 正方体、圆柱、三棱锥、圆锥
D. 正方体、圆柱、四棱柱、圆锥
A
1
2
3
4
5
6
7
8
9
10
11
12
3. 下列图形中,经过折叠不能得到三棱柱的是( C )
C
1
2
3
4
5
6
7
8
9
10
11
12
4. 如图所示是某长方体形状包装盒的表面展开图,根据图中
的数据,该包装盒的容积是(包装盒材料的厚度忽略不
计)( A )
A. 40×70×80 B. 80×80×40
C. 40×40×70 D. 70×70×80
(第4题)
A
1
2
3
4
5
6
7
8
9
10
11
12
5. [2024南京鼓楼区二模]把如图①所示的正三棱锥沿其中的
三条棱剪开后,形成的平面展开图为图②.若剪开的三条
棱中有两条是 AB , AC ,则剪开的另一条棱是
(写出所有正确的答案).
CD 或
BD
(第5题)
1
2
3
4
5
6
7
8
9
10
11
12
6. [母题·教材P15习题T1·2024·济南历下区期末]如图,六个
平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相
等的三角形)的表面展开图,请你把立体图形与它的表面
展开图用线连起来(不考虑尺寸).
1
2
3
4
5
6
7
8
9
10
11
12
7. 一个圆柱无盖铁皮水桶,底面半径为2 dm,高是直径的
1.5倍,现在把它外面都涂漆,求涂漆的面积.
【解】由题意知水桶的高为2×2×1.5=6(dm),底面面积
为π·22=4π(dm2),
则水桶的侧面面积为2π·2×6=24π(dm2),
所以涂漆的面积是24π+4π=28π(dm2).
【点拨】
首先明确涂漆部分的面积是圆柱的侧面面积与一个底
面面积的和,再根据圆柱的侧面面积与底面面积公式计算
即可.
1
2
3
4
5
6
7
8
9
10
11
12
8. [2024九江模拟]将如图所示的圆锥的侧面展开,则点 A 和
点 B 在展开图中的相对位置正确的是( C )
(第8题)
C
1
2
3
4
5
6
7
8
9
10
11
12
9. 如图,将图中的阴影部分剪下来,围成一个几何体的侧
面,使 AB , DC 重合,则所围成的立体图形是( D )
(第9题)
1
2
3
4
5
6
7
8
9
10
11
12
10. 如果圆柱的侧面展开图是相邻两边长分别为8,20π的长
方形,那么这个圆柱的体积等于 .
320或800π
1
2
3
4
5
6
7
8
9
10
11
12
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看!
1.2.1 展开与折叠(第2课时)
第一章 丰富的图形世界
北师大2024版数学七年级上册【示范课精品课】
授课教师:********
班 级:********
时 间:********
学习目标
1.了解棱柱、圆柱、圆锥等常见几何体的表面展开图,发展几何直观.
2.能根据展开图判断和制作简单的立体图形,发展空间观念.
展示一段包含各种建筑、生活用品、自然景观等的视频,其中突出展示各种丰富多样的图形元素,如建筑物中的正方体、圆柱形状的柱子,生活中的球体篮球、长方体的盒子,自然界中的圆形的花朵、三角形的山峰等。
提问学生:“在这段视频中,你们都看到了哪些不同形状的物体?这些物体的形状可以如何分类呢?” 引导学生观察并思考,从而引出本节课的主题 —— 丰富的图形世界。
让学生分享自己在生活中还见过哪些独特的图形,激发学生对图形的兴趣和好奇心。
(二)认识立体图形(10 分钟)
展示正方体、长方体、圆柱、圆锥、球等常见立体图形的实物模型和图片。
分别介绍每种立体图形的名称,并引导学生观察它们的特征,从面的形状、数量,棱的数量、长度关系,顶点的数量等方面进行描述。
正方体:有 6 个完全相同的正方形面,12 条棱长度都相等,8 个顶点。
长方体:有 6 个面,相对的面完全相同,一般情况下 6 个面都是长方形(特殊情况有两个相对的面是正方形),12 条棱,相对的棱长度相等,8 个顶点。
圆柱:有两个底面,是完全相同的圆,侧面是一个曲面,展开后是一个长方形。
圆锥:有一个底面,是一个圆,侧面是一个曲面,展开后是一个扇形,有一个顶点。
球:由一个曲面围成,球面上任意一点到球心的距离都相等。
组织学生分想象是否正确。
5
课堂检测
4
新知讲解
6
变式训练
7
中考考法
8
小结梳理
9
布置作业
学习目录
1
复习引入
2
新知讲解
3
典例讲解
课堂导入
在我们日常生活中,随处可见各种立体图形.
问题
牛奶盒、谷堆可由什么样的平面图形组成
探究新知
问题1 将图中的棱柱沿某些棱剪开,展开成一个平面图形,你能得到哪些形状的平面图形?
知识点 1
棱柱的展开图
探究新知
展开
展开
展开
探究新知
棱柱展开后的特征:
1.棱柱有上下两个底面,它们的形状相同.
2.棱柱侧面的形状都是平行四边形.
3.棱柱侧面的个数和底面图形的边数相等.
4.棱柱所有侧棱长都相等.
总结:
探究新知
拓展:将图中的棱锥沿某些棱剪开,展开成一个平面图形,你能得到哪些形状的平面图形?
展 开
三棱锥的平面展开图
探究新知
展 开
四棱锥的平面展开图
探究新知
展 开
五棱锥的平面展开图
探究新知
五棱柱
折 叠
底面
侧棱
侧面
问题2 下图折叠后的立体图形是什么?
探究新知
练一练 以下哪些图形经过折叠可以围成一个棱柱
⑴
⑵
⑶
⑷
探究新知
知识点 2
圆柱、圆锥的展开图
圆柱展开后的平面图形是什么样的?
思考1 圆柱侧面展开后,得到的平面图形是什么样的?
探究新知
结论:圆柱展开图是由两个等圆和一个长方形组成,其中侧面展开图的一边的长是底面圆的周长,另一边的长是圆柱的高.
思考2 圆柱展开后的平面图形是什么样的?
探究新知
圆锥展开后的平面图形是什么样的?
思考1 圆锥侧面展开后的平面图形是什么样的?
探究新知
总结:圆锥的表面展开图是由扇形和一个圆(底面)组成,其中扇形的半径是圆锥母线(即圆锥底面圆周上任一点与顶点的连线)长,而扇形的弧长则是圆锥底面圆的周长.
思考2 圆锥展开后的平面图形是什么样的?
探究新知
练一练 下面几个图形是一些常见几何体的展开图,你能正确说出这些几何体的名字吗?
长方体
三棱柱
圆柱
探究新知
素养考点 1
立体图形的展开与折叠
方法点拨: 由上、下底面的多边形类型可判断是几棱柱,其他类型的几何体则应记住其表面展开图的主要特征.
例1 如图是立体图形的展开图,你能说出这些立体图形的名称吗?
解:(1)长方体;(2)圆锥;(3)五棱柱;(4)三棱柱.
巩固练习
变式训练
下列图形中可以作为三棱柱的展开图的是( )
A
A.
D.
C.
B.
素养考点 2
利用表面展开图的有关数据进行计算
探究新知
例2 如图是一种食品包装盒的表面展开图.
(1)请写出这个包装盒的形状的名称:____________ .
(2)根据图中所标的尺寸,计算这个食品包装盒的表面积.
三棱柱
探究新知
解:
(2)因为AB=5,AD=3,BE=4,DF=6,
方法点拨:此题是将动手操作和计算相结合,了解立体图形表面展开图与立体图形间的关系,掌握图形面积的计算(公式)是解本题的关键.由表面展开图可知立体图形的表面积等于表面展开图各部分图形面积之和.
(1)三棱柱.
所以侧面积为3×6+5×6+4×6=18+30+24=72,
底面积为 .
所以这个食品包装盒的表面积为72+12=84.
1. [2024邢台期末]圆柱的表面展开图可能是( D )
D
1
2
3
4
5
6
7
8
9
10
11
12
2. [母题·教材P15习题T1]如图,四个图形是由立体图形展开
得到的,相应的立体图形顺次是( A )
A. 正方体、圆柱、三棱柱、圆锥
B. 正方体、圆锥、三棱柱、圆柱
C. 正方体、圆柱、三棱锥、圆锥
D. 正方体、圆柱、四棱柱、圆锥
A
1
2
3
4
5
6
7
8
9
10
11
12
3. 下列图形中,经过折叠不能得到三棱柱的是( C )
C
1
2
3
4
5
6
7
8
9
10
11
12
4. 如图所示是某长方体形状包装盒的表面展开图,根据图中
的数据,该包装盒的容积是(包装盒材料的厚度忽略不
计)( A )
A. 40×70×80 B. 80×80×40
C. 40×40×70 D. 70×70×80
(第4题)
A
1
2
3
4
5
6
7
8
9
10
11
12
5. [2024南京鼓楼区二模]把如图①所示的正三棱锥沿其中的
三条棱剪开后,形成的平面展开图为图②.若剪开的三条
棱中有两条是 AB , AC ,则剪开的另一条棱是
(写出所有正确的答案).
CD 或
BD
(第5题)
1
2
3
4
5
6
7
8
9
10
11
12
6. [母题·教材P15习题T1·2024·济南历下区期末]如图,六个
平面图形中,有圆柱、圆锥、三棱柱(它的底面是三边相
等的三角形)的表面展开图,请你把立体图形与它的表面
展开图用线连起来(不考虑尺寸).
1
2
3
4
5
6
7
8
9
10
11
12
7. 一个圆柱无盖铁皮水桶,底面半径为2 dm,高是直径的
1.5倍,现在把它外面都涂漆,求涂漆的面积.
【解】由题意知水桶的高为2×2×1.5=6(dm),底面面积
为π·22=4π(dm2),
则水桶的侧面面积为2π·2×6=24π(dm2),
所以涂漆的面积是24π+4π=28π(dm2).
【点拨】
首先明确涂漆部分的面积是圆柱的侧面面积与一个底
面面积的和,再根据圆柱的侧面面积与底面面积公式计算
即可.
1
2
3
4
5
6
7
8
9
10
11
12
8. [2024九江模拟]将如图所示的圆锥的侧面展开,则点 A 和
点 B 在展开图中的相对位置正确的是( C )
(第8题)
C
1
2
3
4
5
6
7
8
9
10
11
12
9. 如图,将图中的阴影部分剪下来,围成一个几何体的侧
面,使 AB , DC 重合,则所围成的立体图形是( D )
(第9题)
1
2
3
4
5
6
7
8
9
10
11
12
10. 如果圆柱的侧面展开图是相邻两边长分别为8,20π的长
方形,那么这个圆柱的体积等于 .
320或800π
1
2
3
4
5
6
7
8
9
10
11
12
课堂小结
课后作业
作业
内容
教材作业
从课后习题中选取
自主安排
配套练习册练习
谢谢观看!
同课章节目录
