(小升初重点校分班考)小升初重点校分班考高频考点预测卷-2024-2025学年六年级下册数学人教版(含解析)
文档属性
| 名称 | (小升初重点校分班考)小升初重点校分班考高频考点预测卷-2024-2025学年六年级下册数学人教版(含解析) |  | |
| 格式 | docx | ||
| 文件大小 | 480.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 09:27:54 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
2024-2025学年六年级下册数学小升初重点校分班考预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、单选题
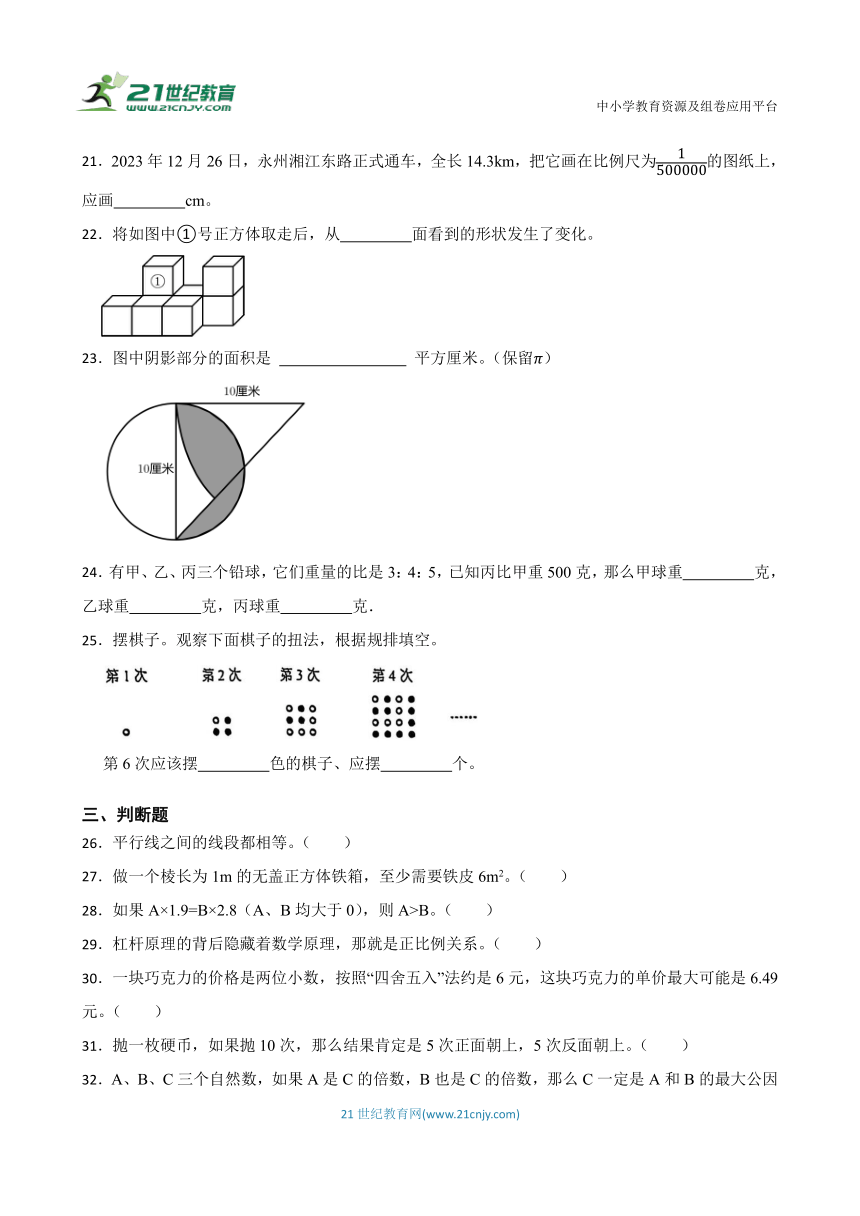
1.如下图所示,若公园在少年宫的正东方向,则公园不可能在医院的( )方向。
A.东偏北50° B.北偏东65° C.北偏东50° D.东偏北35°
2.在下面的统计图中,横线所在位置能反映这4个数的平均数的图是( )。
A. B. C.
3.一个长方体水池,长20米,宽10米,深2米,该水池占地面积是( )m3。
A.40 B.200 C.400 D.520
4.某十字路口处交通信号灯设置为红灯30秒,绿灯50秒,黄灯3秒,则聪聪一家驾车前往高铁站途经该路口时,遇到( )的可能性最大。
A.红灯 B.绿灯 C.黄灯 D.无法判断
5.修路队修一条路。已修长度和未修长度的比是2 :3,再修32 千米刚好到中点。这条路全长( )千米。
A.64 B.320 C.640
6.如下图,王老师开车从家去距离5千米处的药店买口罩和药物,从所给的折线统计图可以看出:停车和买口罩、药物一共用了 分钟,返回时的速度是 千米/时。
A.15 B.30 C.45 D.60
7.学校买了红花、黄花、蓝花准备摆在花坛里,其中红花24盆,( ),学校这三种花共买了多少盆?要解决这个问题,括号里可以补充的信息是( )。
A.黄花、蓝花的总数比红花多20% B.三种花的总数是蓝花的6倍
C.红花比黄花多买了10盆 D.黄花和蓝花的数量比为3:5
8. 超市运回一批糖果,第一次运走了,第二次运走了余下的。两次运走的相比,( )。
A.第一次多 B.第二次多 C.一样多 D.无法比较
9.图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子,能倒满( )怀。
A.2 B.3 C.4 D.6
10.幻方是古老的数学问题,我国古代《洛书》中记载了最早的幻方一九宫格。将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等。如下图,图①就是一个幻方,图②是一个未完成的幻方,则m与n的和是( )。
A.9 B.10 C.11 D.12
二、填空题
11.六(2)班男生人数的 和女生人数的60%相等,男、女生人数的最简整数比是 ,如果男生有16人,那么六(2)班有 人。
12.把6千克桃子平均分给5个人,每人分得这些桃子的 ,每人分得 千克。
13.根据■÷▲=20,在括号里填上合适的数。
(■×5)÷(▲×5)= (■×3)÷▲=
14.下图中阴影部分的面积是 ,空白部分的面积是 。整个图形的面积是 。
15.从12的因数中选出四个数,组成比例是 。(任写一个)
16.看图填空。
▲的个数是■的,▲的个数比■少( )%。
17.把一根3米长的绳子对折2次,每段占全长的(填分数),每段绳长( )米。
18.鸡蛋中含有丰富的营养成分,一个鸡蛋各部分质量统计如下图。丽丽每天早晨都吃一个鸡蛋(一个鸡蛋大约重0.06千克),丽丽每天摄入的蛋白有 克,蛋黄有 克。
19.计算 运用了乘法 律;计算 4,运用了乘法 律。
20.用4个同样的小正方体拼成一个长方体(如下图),表面积减少了每个小正方体的体积是 cm3,拼成的长方体的体积是 cm3。
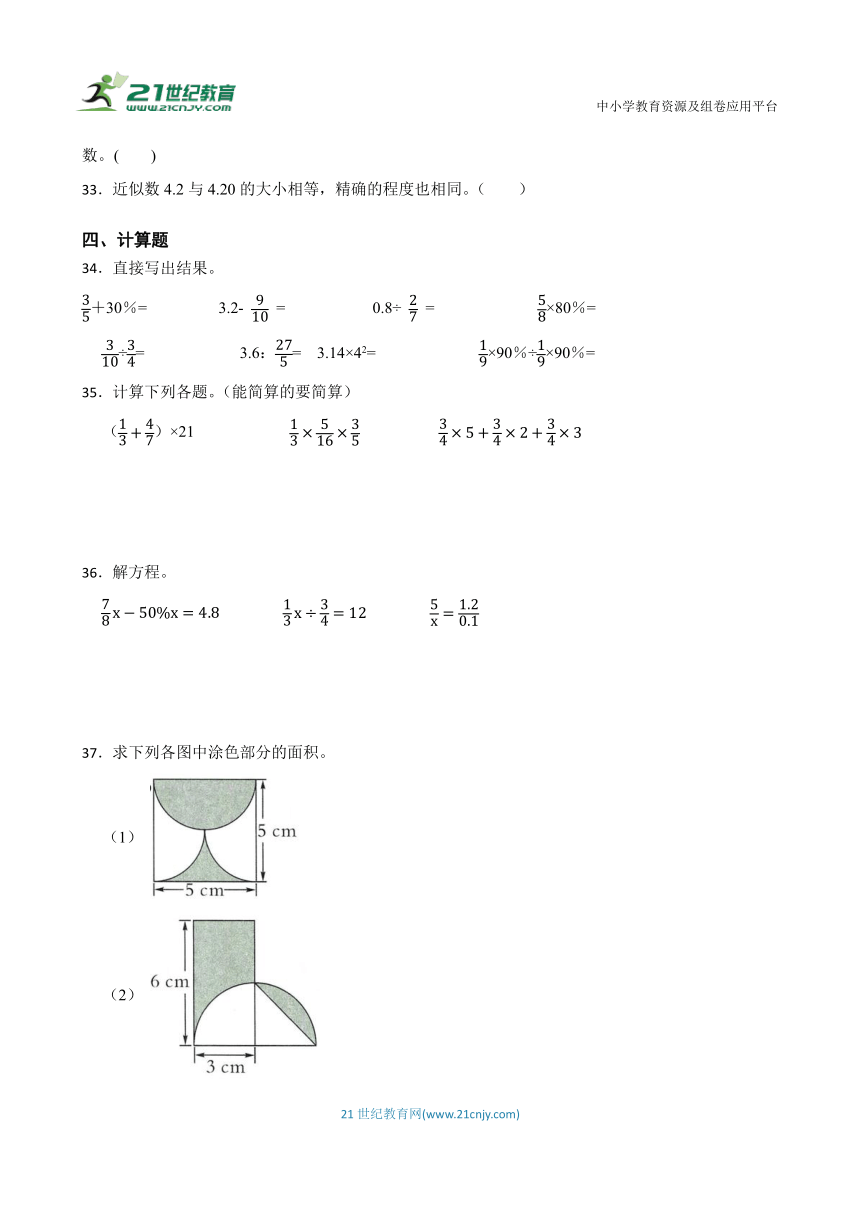
21.2023年12月26日,永州湘江东路正式通车,全长14.3km,把它画在比例尺为的图纸上,应画 cm。
22.将如图中①号正方体取走后,从 面看到的形状发生了变化。
23.图中阴影部分的面积是 平方厘米。(保留)
24.有甲、乙、丙三个铅球,它们重量的比是3:4:5,已知丙比甲重500克,那么甲球重 克,乙球重 克,丙球重 克.
25.摆棋子。观察下面棋子的扭法,根据规排填空。
第6次应该摆 色的棋子、应摆 个。
三、判断题
26.平行线之间的线段都相等。( )
27.做一个棱长为1m的无盖正方体铁箱,至少需要铁皮6m2。( )
28.如果A×1.9=B×2.8(A、B均大于0),则A>B。( )
29.杠杆原理的背后隐藏着数学原理,那就是正比例关系。( )
30.一块巧克力的价格是两位小数,按照“四舍五入”法约是6元,这块巧克力的单价最大可能是6.49元。( )
31.抛一枚硬币,如果抛10次,那么结果肯定是5次正面朝上,5次反面朝上。( )
32.A、B、C三个自然数,如果A是C的倍数,B也是C的倍数,那么C一定是A和B的最大公因数。( )
33.近似数4.2与4.20的大小相等,精确的程度也相同。( )
四、计算题
34.直接写出结果。
+30%= 3.2- = 0.8÷ = ×80%=
÷= 3.6:= 3.14×42= ×90%÷×90%=
35.计算下列各题。(能简算的要简算)
()×21
36.解方程。
37.求下列各图中涂色部分的面积。
(1)
(2)
五、作图题
38.
(1)用数对表示三角形ABC三个顶点的位置,A点是 ,B点是 ,C点是 。
(2)三角形ABC先向左平移3格,再向上平移5格后得到的新图形是三角形A B C 。画出三角形A B C 。并用数对表示三角形A B C 的顶点的位置。
六、解决问题
39.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,原计划每小时生产多少个零件?
40.张老师想在网上购买30本《世界未解之谜》,为班级图书角添置新书。淘宝价格26元/本,购书数量不超过50本时,邮费都是10元。淘宝上有促销活动:每买5本,赠送1本,包邮。
(1)不参加促销活动,一共要付多少元钱?
(2)参加促销活动,怎样买合算?需要付多少元钱?
41.李红一家去南宁游玩,要先乘2时的汽车到贺州站,再乘3时的动车才到达南宁。李红家到南宁一共有多少千米?
汽车每时行50千米,动车每时行141千米。
42.为了丰富居民的日常生活,阳光小区附近修建了一个正方形广场。如果用边长是0.6米的方砖铺地,需要600块;如果改用边长是0.8米的方砖铺地,需要方砖多少块?(用比例方法解答)
43.5位老师带领45名小学生参观科技馆,科技馆门票的价格如图。请你设计两种不同的买票方案,并计算出你设计的买票方案应付多少元?
门票 成人票:20元/人 学生票:4元/人
团体票:5元/人(50人及以上)
44.寒暑表上通常有两个刻度,摄氏度(记为℃)和华氏度(记为),它们之间的换算关系是:摄氏度华氏度,那么在摄氏多少度时,华氏度的值恰好比摄氏度的值大.
45.某家电城上午售出4台洗衣机,下午售出同样的洗衣机7台,上午比下午少收货款3150元。平均每台洗衣机售价多少元?
46.洛阳水席始于唐代,是中国迄今保留下来的历史久远的名宴之一。某店准备了117份水席套餐,当天卖出了后,剩下的套餐被甲、乙两个旅游团团购完,若甲、乙两个旅游团购买的份数比为7:6,则甲、乙两个旅游团各应付多少元
洛阳水席套餐
单价: 250元/份 团购价: 每份降价
47.奇奇在陪奶奶聊天,得知奶奶们要代表敬老院参加广场舞比赛。每人需准备一条底边为1.6米,对应高为70厘米的三角形披肩,奶奶们打算买布料自己做。已知4平方分米的布料需要1元(不考虑裁剪与制作损耗),奶奶们每人需要花费多少元?
48.客车和货车同时从相距480千米的甲、乙两地相对开出,经过3小时两车相遇,客车和货车的速度比是5:3。客车和货车每小时分别行多少千米 ?
参考答案及试题解析
1.【答案】A
【解析】解:据图可知,少年宫在医院的东偏北45°方向,又因为公园在少年宫的正东方向,因此若将公园与医院连线,则其与正东方向的夹角小于45°,因此公园不可能在医院的东偏北50°方向。
故答案为:A
【分析】先根据少年宫的位置确定公园的大致位置,将公园与医院连线连线和正东方向的轴的夹角应该小于和少年宫的夹角45度。东偏北50大于45度所以A错。
2.【答案】C
3.【答案】B
【解析】解:20×10=200(平方米)
故答案为:B。
【分析】用游泳池的长乘宽即可求出底面积,也就是游泳池的占地面积。
4.【答案】B
【解析】因为绿灯显示时间最长,则经过该路口时候遇见绿灯的可能性最大。
故答案为:B.
【分析】 此题考查的是概率与可能性的概念,具体是交通信号灯不同颜色显示时间的长短与遇到该颜色信号灯可能性大小的关系。从题目给出的条件来看,我们可以直接根据各颜色信号灯的显示时间长短来判断遇到该颜色信号灯的可能性大小,因为可能性大小与显示时间的长短成正比。
5.【答案】B
【解析】解:2+3=5
32÷(-)
=32÷
=320(千米)
故答案为:B
【分析】已修长度和未修长度的比是2:3,把总长度看作单位“1”,再修之前的已修长度占总长度的,再修32千米刚好到中点,即总长度的,再修32千米对应的分率为-,对应的具体数量是32千米。
6.【答案】D;A
【解析】解:停车和买口罩、药物用了:(40-20)+(100-60)
=20+40
=60(分钟);
返回的时间:120-100=20(分)=时
返回时的速度:5÷=15(千米/时);
故答案为:D;A。
【分析】由折线图可以看出,王老师在20~40分钟和60~100分钟时停车和买口罩、药物,分别计算出这两段时间再相加即可;路程是5千米,100分~120分是返回时间,求速度,用路程除以时间。
7.【答案】A
【解析】解:A:这个条件可以求出共买的盆数;
B:不知道蓝花的盆数,无法计算出总盆数;
C:无法计算蓝花的盆数,就无法计算总盆数;
D:只知道黄花和蓝花的数量比,无法计算黄花和蓝花的盆数,无法计算总盆数。
故答案为:A。
【分析】A选项中:用红花盆数乘(1+20%)求出黄花和蓝花的盆数,然后相加求出三种花的总数。
8.【答案】C
【解析】解:(1-)×
=×
=
=,两次运走的一样多。
故答案为:C。
【分析】第二次运走的分率=(1-第一次运走的分率)×余下的分率,然后比较大小。
9.【答案】D
【解析】解:3×2=6(杯)。
故答案为:D。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的底面积相等,圆柱的高是圆锥高的2倍时,圆柱的体积是圆锥体积的3×2=6倍。
10.【答案】D
【解析】解:由第一行知,每行相加等于26+m;
第三行第一个:m+6+20-(m+22)=4;
第二行第二个:26+m-22-n=4+m-n;
第三行第二个:26+m-6-(4+m-n)=16+n;
第三行第三个:26+m-20-n=6+m-n;
对角线相加:m+4+m-n+6+m-n=26+m
2m-2n=16
m-n=8
所以第二行第二个数是:4+8=12;
第三行第三个数是:6+8=14;
对角线相加:20+12+4=26+m
m=10
因为m-n=8,所以n=2,那么m+n=12。
故答案为:D。
【分析】每行相加等于26+m;据此每个空白处的数字用含有m的字母代替,从而求出各数,最后计算出m+n=12。
11.【答案】4:5;36
【解析】解:第一问:60%:=60:75=4:5;
第二问:16×÷60%
=12÷60%
=20(人)
16+20=36(人)。
故答案为:4:5;36。
【分析】第一问:男生人数×=女生人数×60%,所以写出60%与的比并化成最简整数比就是男生和女生的人数比。
第二问:用男生人数乘,然后除以60%即可求出女生人数,进而求出这个班的总人数。
12.【答案】;
13.【答案】20;60
14.【答案】(a-c)b;bc;ab
【解析】解:阴影部分的面积:(a-c)b,
空白部分的面积:bc,
整个图形的面积:ab。
故答案为:(a-c)b;bc;ab。
【分析】阴影部分面积 = 长 × 宽 ,空白部分面积 = 整个图形面积 - 阴影部分面积 ,整个图形的面积等于大长方形的面积,长方形的面积=长×宽,据此解答。
15.【答案】6:3=4:2
【解析】解:12的因数:1,2,3,4,6,12
比例:6:3=4:2
故答案为:6:3=4:2。
【分析】因数 ,也称约数、因子、除子,用于描述整数之间存在的整除关系。具体来说,如果整数n可以被另一个非零整数m整除,且商为整数,那么我们称m是n的一个因数;据此列出12的所有因数:1,2,3,4,6,12;然后根据两个比值相等的比可以组成比例,发现4和2、6和3的比值都是2,所以可以组成比例6:3=4:2。
16.【答案】;37.5
17.【答案】;
18.【答案】31.8;19.2
【解析】解:0.06千克=60克,丽丽每天摄入的蛋白有60×53%=31.8(克),蛋黄有60×32%=19.2(克)。
故答案为:31.8;19.2。
【分析】把0.6千克换算成60克,用一个鸡蛋的重量乘53%即可求出蛋白的质量,用一个鸡蛋的质量乘32%即可求出蛋黄的重量。
19.【答案】交换;结合
【解析】解:交换了后面两个因数的位置,运用了乘法交换律;
4,添了括号让后面两数先乘,运用了乘法结合律;
故答案为:交换;结合。
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或者先把后两个数相乘,再和另外一个数相乘,积不变的乘法运算方法。两个数相乘,交换因数的位置,它们的积不变,叫做乘法交换律。
20.【答案】8;32
【解析】解: 32÷8=4cm 2,
a2=4,a=2cm ,
V=23=8 cm3;
4×8=32cm3.
故答案为:8;32。
【分析】4个小正方体拼长方体,减少8个面,共减少32cm2, 则一个面面积是4cm2, 由正方形面积公式S=a2,得小正方体棱长为2cm ,根据正方体体积公式V=a3,得出小正方体体积。
21.【答案】2.86
22.【答案】正
23.【答案】(25π-50)
【解析】解:在直角三角形中,AB=AC=10厘米;所以∠C=45°
△ABC是等腰直角三角形,
10×10÷2-π×102×=(50-12.5π)(平方厘米)
π×(10÷2)2÷2-(50-12.5π)
=12.5π-50+12.5π
=(25π-50)(平方厘米)。
故答案为:(25π-50)。
【分析】阴影面积①面积④面积半圆面积②面积;其中,②面积=△ABC面积扇形AEC面积,半圆面积=圆的面积÷2。
24.【答案】750;1000;1250
【解析】500÷(5-3)
=500÷2
=250(克)
甲:250×3=750(克)
乙:250×4=1000(克)
丙:250×5=1250(克)
故答案为:750;1000;1250
【分析】用丙比甲重的重量除以丙与甲的份数差,求出每份是多少克,然后用每份的重量分别乘三个球的份数即可分别求出三个球的重量.
25.【答案】黑;36
【解析】解:6×6=36(个),第6次应该摆黑色的棋子,应摆的个数是36个。
故答案为:黑;36。
【分析】第一次是白色1颗,第二次黑色2颗,第三次白色3颗,第四次黑色4颗,第五次白色5颗······棋子颜色的交替规律是:白色、黑色、白色、黑色······如此交替。第n次摆的个数=n2个。
26.【答案】错误
【解析】解:平行线之间的距离都相等。
故答案为:错误。
【分析】平行线之间的距离是平行线之间的垂直线段,而这些垂直线段是相等的。
27.【答案】错误
【解析】解:1×1×5
=1×5
=5(m2),
所以做一个棱长为1m的无盖正方体铁箱,至少需要铁皮5m2,即原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,本题中无盖正方体铁箱,所以只求5个面的面积,即棱长×棱长×5,计算即可得出答案。
28.【答案】正确
【解析】解:A×1.9=B×2.8,因为1.9<2.8,所以A>B。原题说法正确。
故答案为:正确。
【分析】积相等,一个因数较小的,另一个因数就较大。
29.【答案】错误
【解析】解:杠杆原理:动力×动力臂=阻力×阻力臂,根据杠杆原理可以确定杠杆原理背后隐藏着数学原理是反比例关系。
故答案为:错误。
【分析】两种相关联的量,若其比值一定,两种量成正比例关系;若其乘积一定,两种量成反比例关系。
30.【答案】正确
【解析】解:这块巧克力的单价最大可能是6.49元。
故答案为:错误。
【分析】把一个小数保留整数,就是把这个小数十分位上的数进行四舍五入即可。
31.【答案】错误
【解析】解:抛一枚硬币,如果抛10次,那么结果可能是5次正面朝上,5次反面朝上,原题干说法错误。
故答案为:错误。
【分析】抛一枚硬币,有正反两面,任意抛一次,两种情况都有可能发生,所以如果抛10次,那么结果可能是5次正面朝上,5次反面朝上;还可能是其它情况。
32.【答案】错误
33.【答案】错误
【解析】
近似数4.2与4.20的大小相等,精确的程度不相同,本题错。
故答案为:错误。
【分析】4.2精确到十分位,4.20精确到百分位。
34.【答案】+30%=0.9 3.2-=2.3 0.8÷= ×80%=0.5
÷= 3.6:= 3.14×42=50.24 ×90%÷×90%=0.81
【解析】含百分数的计算,把百分数化成分数或小数,然后再计算;求比值,用比的前项除以比的后项;分数、百分数乘除混合运算,按照从左到右的顺序计算。
35.【答案】解: ()×21
=×21+×21
=7+12
=19
=××
=×
=
=×(5+2+3)
=×10
=
【解析】观察数据可知,此题应用乘法分配律简算;
观察数据可知,此题应用乘法交换律和结合律,可以使计算简便;
观察数据可知,此题应用乘法分配律简算。
36.【答案】
解:
解:
解:1.2x=5×0.1
1.2x=0.5
x=
【解析】等式的基本性质1:等式两边同时加上或减去同一个数,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立。
比例的基本性质:两个内项的积等于两个外项的积。
(1)先将百分数化为分数,得到,然后计算等式左边得到,最后根据等式的基本性质2,将等式两边同时除以,即可得到答案;
(2)先计算等式左边的除法,得到,再根据等式的基本性质2,将等式两边同时除以,即可得到答案;
(3)先根据比例的基本性质,得到1.2x=50.1,然后计算等式右边的小数乘法,得到1.2x=0.5,再根据等式的基本性质2,将等式两边同时除以1.2,即可得到答案。
37.【答案】(1)解:5×5÷2=12.5(cm2)
(2)解:(6-3+6)×3÷2= 13.5(cm2)
【解析】(1)观察图形,下半部分的阴影与上半部分的半圆形阴影可以拼成一个完整的长方形,占正方形面积的一半;计算出正方形面积再除以2即可。
(2)将右边扇形中的阴影部分移动到半圆形的左半边,发现刚好可以与长方形中的阴影部分拼成一个直角梯形;由于圆的半径是固定的,可知梯形的上底为6-3;利用梯形面积公式,代入数值计算即可。
38.【答案】(1)(6,4);(9,4);(4,1)
(2)解:如图所示:
【解析】用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图。
39.【答案】解:设原计划每小时生产x个零件,
依题意得:13x=12(x+10)-60,
解得:x=60.
答:原计划每小时生产60个零件.
【解析】设原计划每小时生产x个零件,根据每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,原计划13小时生产的零件数=实际12小时生产的零件-60,列出方程,求解即可.
40.【答案】(1)790元
(2)买5组“买五送一”,需要付650元
41.【答案】解:50×2+141×3
=100+423
=523(千米)
答:李红家到南宁一共有523千米。
【解析】李红家到南宁一共的路程=汽车的速度×汽车行驶的时间+动车的速度×动车行驶的时间。
42.【答案】337.5块
43.【答案】解:方案一:5×20+45×4
=100+180
=280(元)
方案二:5+45=50(人)
50×5=250(元)
答:5位老师买成人票,45名学生买学生票,应付280元;买50张团体票,应付250元。
【解析】方案一总价=成人的人数×成人票单价+学生人数×学生票单价;方案二总价=(成人的人数+学生人数)×团体票单价。
44.【答案】解:设在摄氏x度时,华氏度的值恰好比摄氏度的值大60,可得,
答:在摄氏35度时,华氏度的值恰好比摄氏度的值大60
【解析】设在摄氏x℃时,华氏度的值恰好比摄氏度的值大60。
根据题目给出的换算公式,可以列出方程:,然后解方程即可
45.【答案】解:3150÷(7-4)
=3150÷3
=1050(元)
答:平均每台洗衣机售价1050元。
【解析】上午比下午收货款少,是因为上午比下午少卖了(7-4)台,用少收的货款数除以少卖的台数即可求出平均每台的售价。
46.【答案】解:甲、乙两个旅游团购买了:117×(1-)=13(份)
每份水席套餐团购价:250×(1-)=200(元)
甲旅游团应付:13××200=1400(元)
乙旅游团应付: 13××200=1200(元)
答:甲旅游团应付1400元,乙旅游团应付 1200 元。
【解析】求卖了一后剩余水席套餐的份数和团购价格,再求将这剩余的水席套餐卖给甲、乙两个旅游团各多少份,再乘以团购价即可。
47.【答案】解:1.6米=16分米,70厘米=7分米。
披肩面积16×7÷2=56(平方分米),
需要金额:56÷4=14(元),
答:奶奶们每人需要花费14元。
【解析】 本题考查了三角形面积公式在实际生活中的应用以及单位换算。先根据面积公式底×高÷2求出披肩的面积,再根据布料价格求出所需费用,解题过程中要注意单位的统一,将米和厘米都换算成分米,方便计算。
48.【答案】解:客车:
=160×
=100(千米)
货车:480÷3-100=60(千米)
答:客车每小时行100千米,货车每小时行60千米。
【解析】用两地的距离除以相遇时间求出速度和,然后把速度和按照5:3的比分配后分别求出客车和货车每小时分别行的路程。
21世纪教育网(www.21cnjy.com)
2024-2025学年六年级下册数学小升初重点校分班考预测卷
考试时间:90分钟;试卷总分:100分;
学校: 班级: 姓名: 成绩:
注意事项:
答题前填写好自己的姓名、班级、考号等信息。
请将答案正确填写在答题区域,注意书写工整,格式正确,卷面整洁。
一、单选题
1.如下图所示,若公园在少年宫的正东方向,则公园不可能在医院的( )方向。
A.东偏北50° B.北偏东65° C.北偏东50° D.东偏北35°
2.在下面的统计图中,横线所在位置能反映这4个数的平均数的图是( )。
A. B. C.
3.一个长方体水池,长20米,宽10米,深2米,该水池占地面积是( )m3。
A.40 B.200 C.400 D.520
4.某十字路口处交通信号灯设置为红灯30秒,绿灯50秒,黄灯3秒,则聪聪一家驾车前往高铁站途经该路口时,遇到( )的可能性最大。
A.红灯 B.绿灯 C.黄灯 D.无法判断
5.修路队修一条路。已修长度和未修长度的比是2 :3,再修32 千米刚好到中点。这条路全长( )千米。
A.64 B.320 C.640
6.如下图,王老师开车从家去距离5千米处的药店买口罩和药物,从所给的折线统计图可以看出:停车和买口罩、药物一共用了 分钟,返回时的速度是 千米/时。
A.15 B.30 C.45 D.60
7.学校买了红花、黄花、蓝花准备摆在花坛里,其中红花24盆,( ),学校这三种花共买了多少盆?要解决这个问题,括号里可以补充的信息是( )。
A.黄花、蓝花的总数比红花多20% B.三种花的总数是蓝花的6倍
C.红花比黄花多买了10盆 D.黄花和蓝花的数量比为3:5
8. 超市运回一批糖果,第一次运走了,第二次运走了余下的。两次运走的相比,( )。
A.第一次多 B.第二次多 C.一样多 D.无法比较
9.图中,瓶底的面积和锥形杯口的面积相等,将瓶子中的液体倒入锥形杯子,能倒满( )怀。
A.2 B.3 C.4 D.6
10.幻方是古老的数学问题,我国古代《洛书》中记载了最早的幻方一九宫格。将9个数填入幻方的空格中,要求每一横行、每一竖列以及两条对角线上的3个数之和相等。如下图,图①就是一个幻方,图②是一个未完成的幻方,则m与n的和是( )。
A.9 B.10 C.11 D.12
二、填空题
11.六(2)班男生人数的 和女生人数的60%相等,男、女生人数的最简整数比是 ,如果男生有16人,那么六(2)班有 人。
12.把6千克桃子平均分给5个人,每人分得这些桃子的 ,每人分得 千克。
13.根据■÷▲=20,在括号里填上合适的数。
(■×5)÷(▲×5)= (■×3)÷▲=
14.下图中阴影部分的面积是 ,空白部分的面积是 。整个图形的面积是 。
15.从12的因数中选出四个数,组成比例是 。(任写一个)
16.看图填空。
▲的个数是■的,▲的个数比■少( )%。
17.把一根3米长的绳子对折2次,每段占全长的(填分数),每段绳长( )米。
18.鸡蛋中含有丰富的营养成分,一个鸡蛋各部分质量统计如下图。丽丽每天早晨都吃一个鸡蛋(一个鸡蛋大约重0.06千克),丽丽每天摄入的蛋白有 克,蛋黄有 克。
19.计算 运用了乘法 律;计算 4,运用了乘法 律。
20.用4个同样的小正方体拼成一个长方体(如下图),表面积减少了每个小正方体的体积是 cm3,拼成的长方体的体积是 cm3。
21.2023年12月26日,永州湘江东路正式通车,全长14.3km,把它画在比例尺为的图纸上,应画 cm。
22.将如图中①号正方体取走后,从 面看到的形状发生了变化。
23.图中阴影部分的面积是 平方厘米。(保留)
24.有甲、乙、丙三个铅球,它们重量的比是3:4:5,已知丙比甲重500克,那么甲球重 克,乙球重 克,丙球重 克.
25.摆棋子。观察下面棋子的扭法,根据规排填空。
第6次应该摆 色的棋子、应摆 个。
三、判断题
26.平行线之间的线段都相等。( )
27.做一个棱长为1m的无盖正方体铁箱,至少需要铁皮6m2。( )
28.如果A×1.9=B×2.8(A、B均大于0),则A>B。( )
29.杠杆原理的背后隐藏着数学原理,那就是正比例关系。( )
30.一块巧克力的价格是两位小数,按照“四舍五入”法约是6元,这块巧克力的单价最大可能是6.49元。( )
31.抛一枚硬币,如果抛10次,那么结果肯定是5次正面朝上,5次反面朝上。( )
32.A、B、C三个自然数,如果A是C的倍数,B也是C的倍数,那么C一定是A和B的最大公因数。( )
33.近似数4.2与4.20的大小相等,精确的程度也相同。( )
四、计算题
34.直接写出结果。
+30%= 3.2- = 0.8÷ = ×80%=
÷= 3.6:= 3.14×42= ×90%÷×90%=
35.计算下列各题。(能简算的要简算)
()×21
36.解方程。
37.求下列各图中涂色部分的面积。
(1)
(2)
五、作图题
38.
(1)用数对表示三角形ABC三个顶点的位置,A点是 ,B点是 ,C点是 。
(2)三角形ABC先向左平移3格,再向上平移5格后得到的新图形是三角形A B C 。画出三角形A B C 。并用数对表示三角形A B C 的顶点的位置。
六、解决问题
39.某车间原计划13小时生产一批零件,后来每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,原计划每小时生产多少个零件?
40.张老师想在网上购买30本《世界未解之谜》,为班级图书角添置新书。淘宝价格26元/本,购书数量不超过50本时,邮费都是10元。淘宝上有促销活动:每买5本,赠送1本,包邮。
(1)不参加促销活动,一共要付多少元钱?
(2)参加促销活动,怎样买合算?需要付多少元钱?
41.李红一家去南宁游玩,要先乘2时的汽车到贺州站,再乘3时的动车才到达南宁。李红家到南宁一共有多少千米?
汽车每时行50千米,动车每时行141千米。
42.为了丰富居民的日常生活,阳光小区附近修建了一个正方形广场。如果用边长是0.6米的方砖铺地,需要600块;如果改用边长是0.8米的方砖铺地,需要方砖多少块?(用比例方法解答)
43.5位老师带领45名小学生参观科技馆,科技馆门票的价格如图。请你设计两种不同的买票方案,并计算出你设计的买票方案应付多少元?
门票 成人票:20元/人 学生票:4元/人
团体票:5元/人(50人及以上)
44.寒暑表上通常有两个刻度,摄氏度(记为℃)和华氏度(记为),它们之间的换算关系是:摄氏度华氏度,那么在摄氏多少度时,华氏度的值恰好比摄氏度的值大.
45.某家电城上午售出4台洗衣机,下午售出同样的洗衣机7台,上午比下午少收货款3150元。平均每台洗衣机售价多少元?
46.洛阳水席始于唐代,是中国迄今保留下来的历史久远的名宴之一。某店准备了117份水席套餐,当天卖出了后,剩下的套餐被甲、乙两个旅游团团购完,若甲、乙两个旅游团购买的份数比为7:6,则甲、乙两个旅游团各应付多少元
洛阳水席套餐
单价: 250元/份 团购价: 每份降价
47.奇奇在陪奶奶聊天,得知奶奶们要代表敬老院参加广场舞比赛。每人需准备一条底边为1.6米,对应高为70厘米的三角形披肩,奶奶们打算买布料自己做。已知4平方分米的布料需要1元(不考虑裁剪与制作损耗),奶奶们每人需要花费多少元?
48.客车和货车同时从相距480千米的甲、乙两地相对开出,经过3小时两车相遇,客车和货车的速度比是5:3。客车和货车每小时分别行多少千米 ?
参考答案及试题解析
1.【答案】A
【解析】解:据图可知,少年宫在医院的东偏北45°方向,又因为公园在少年宫的正东方向,因此若将公园与医院连线,则其与正东方向的夹角小于45°,因此公园不可能在医院的东偏北50°方向。
故答案为:A
【分析】先根据少年宫的位置确定公园的大致位置,将公园与医院连线连线和正东方向的轴的夹角应该小于和少年宫的夹角45度。东偏北50大于45度所以A错。
2.【答案】C
3.【答案】B
【解析】解:20×10=200(平方米)
故答案为:B。
【分析】用游泳池的长乘宽即可求出底面积,也就是游泳池的占地面积。
4.【答案】B
【解析】因为绿灯显示时间最长,则经过该路口时候遇见绿灯的可能性最大。
故答案为:B.
【分析】 此题考查的是概率与可能性的概念,具体是交通信号灯不同颜色显示时间的长短与遇到该颜色信号灯可能性大小的关系。从题目给出的条件来看,我们可以直接根据各颜色信号灯的显示时间长短来判断遇到该颜色信号灯的可能性大小,因为可能性大小与显示时间的长短成正比。
5.【答案】B
【解析】解:2+3=5
32÷(-)
=32÷
=320(千米)
故答案为:B
【分析】已修长度和未修长度的比是2:3,把总长度看作单位“1”,再修之前的已修长度占总长度的,再修32千米刚好到中点,即总长度的,再修32千米对应的分率为-,对应的具体数量是32千米。
6.【答案】D;A
【解析】解:停车和买口罩、药物用了:(40-20)+(100-60)
=20+40
=60(分钟);
返回的时间:120-100=20(分)=时
返回时的速度:5÷=15(千米/时);
故答案为:D;A。
【分析】由折线图可以看出,王老师在20~40分钟和60~100分钟时停车和买口罩、药物,分别计算出这两段时间再相加即可;路程是5千米,100分~120分是返回时间,求速度,用路程除以时间。
7.【答案】A
【解析】解:A:这个条件可以求出共买的盆数;
B:不知道蓝花的盆数,无法计算出总盆数;
C:无法计算蓝花的盆数,就无法计算总盆数;
D:只知道黄花和蓝花的数量比,无法计算黄花和蓝花的盆数,无法计算总盆数。
故答案为:A。
【分析】A选项中:用红花盆数乘(1+20%)求出黄花和蓝花的盆数,然后相加求出三种花的总数。
8.【答案】C
【解析】解:(1-)×
=×
=
=,两次运走的一样多。
故答案为:C。
【分析】第二次运走的分率=(1-第一次运走的分率)×余下的分率,然后比较大小。
9.【答案】D
【解析】解:3×2=6(杯)。
故答案为:D。
【分析】等底等高的圆柱的体积是圆锥体积的3倍,所以当圆柱和圆锥的底面积相等,圆柱的高是圆锥高的2倍时,圆柱的体积是圆锥体积的3×2=6倍。
10.【答案】D
【解析】解:由第一行知,每行相加等于26+m;
第三行第一个:m+6+20-(m+22)=4;
第二行第二个:26+m-22-n=4+m-n;
第三行第二个:26+m-6-(4+m-n)=16+n;
第三行第三个:26+m-20-n=6+m-n;
对角线相加:m+4+m-n+6+m-n=26+m
2m-2n=16
m-n=8
所以第二行第二个数是:4+8=12;
第三行第三个数是:6+8=14;
对角线相加:20+12+4=26+m
m=10
因为m-n=8,所以n=2,那么m+n=12。
故答案为:D。
【分析】每行相加等于26+m;据此每个空白处的数字用含有m的字母代替,从而求出各数,最后计算出m+n=12。
11.【答案】4:5;36
【解析】解:第一问:60%:=60:75=4:5;
第二问:16×÷60%
=12÷60%
=20(人)
16+20=36(人)。
故答案为:4:5;36。
【分析】第一问:男生人数×=女生人数×60%,所以写出60%与的比并化成最简整数比就是男生和女生的人数比。
第二问:用男生人数乘,然后除以60%即可求出女生人数,进而求出这个班的总人数。
12.【答案】;
13.【答案】20;60
14.【答案】(a-c)b;bc;ab
【解析】解:阴影部分的面积:(a-c)b,
空白部分的面积:bc,
整个图形的面积:ab。
故答案为:(a-c)b;bc;ab。
【分析】阴影部分面积 = 长 × 宽 ,空白部分面积 = 整个图形面积 - 阴影部分面积 ,整个图形的面积等于大长方形的面积,长方形的面积=长×宽,据此解答。
15.【答案】6:3=4:2
【解析】解:12的因数:1,2,3,4,6,12
比例:6:3=4:2
故答案为:6:3=4:2。
【分析】因数 ,也称约数、因子、除子,用于描述整数之间存在的整除关系。具体来说,如果整数n可以被另一个非零整数m整除,且商为整数,那么我们称m是n的一个因数;据此列出12的所有因数:1,2,3,4,6,12;然后根据两个比值相等的比可以组成比例,发现4和2、6和3的比值都是2,所以可以组成比例6:3=4:2。
16.【答案】;37.5
17.【答案】;
18.【答案】31.8;19.2
【解析】解:0.06千克=60克,丽丽每天摄入的蛋白有60×53%=31.8(克),蛋黄有60×32%=19.2(克)。
故答案为:31.8;19.2。
【分析】把0.6千克换算成60克,用一个鸡蛋的重量乘53%即可求出蛋白的质量,用一个鸡蛋的质量乘32%即可求出蛋黄的重量。
19.【答案】交换;结合
【解析】解:交换了后面两个因数的位置,运用了乘法交换律;
4,添了括号让后面两数先乘,运用了乘法结合律;
故答案为:交换;结合。
【分析】乘法结合律是指三个数相乘,先把前两个数相乘,再和另外一个数相乘,或者先把后两个数相乘,再和另外一个数相乘,积不变的乘法运算方法。两个数相乘,交换因数的位置,它们的积不变,叫做乘法交换律。
20.【答案】8;32
【解析】解: 32÷8=4cm 2,
a2=4,a=2cm ,
V=23=8 cm3;
4×8=32cm3.
故答案为:8;32。
【分析】4个小正方体拼长方体,减少8个面,共减少32cm2, 则一个面面积是4cm2, 由正方形面积公式S=a2,得小正方体棱长为2cm ,根据正方体体积公式V=a3,得出小正方体体积。
21.【答案】2.86
22.【答案】正
23.【答案】(25π-50)
【解析】解:在直角三角形中,AB=AC=10厘米;所以∠C=45°
△ABC是等腰直角三角形,
10×10÷2-π×102×=(50-12.5π)(平方厘米)
π×(10÷2)2÷2-(50-12.5π)
=12.5π-50+12.5π
=(25π-50)(平方厘米)。
故答案为:(25π-50)。
【分析】阴影面积①面积④面积半圆面积②面积;其中,②面积=△ABC面积扇形AEC面积,半圆面积=圆的面积÷2。
24.【答案】750;1000;1250
【解析】500÷(5-3)
=500÷2
=250(克)
甲:250×3=750(克)
乙:250×4=1000(克)
丙:250×5=1250(克)
故答案为:750;1000;1250
【分析】用丙比甲重的重量除以丙与甲的份数差,求出每份是多少克,然后用每份的重量分别乘三个球的份数即可分别求出三个球的重量.
25.【答案】黑;36
【解析】解:6×6=36(个),第6次应该摆黑色的棋子,应摆的个数是36个。
故答案为:黑;36。
【分析】第一次是白色1颗,第二次黑色2颗,第三次白色3颗,第四次黑色4颗,第五次白色5颗······棋子颜色的交替规律是:白色、黑色、白色、黑色······如此交替。第n次摆的个数=n2个。
26.【答案】错误
【解析】解:平行线之间的距离都相等。
故答案为:错误。
【分析】平行线之间的距离是平行线之间的垂直线段,而这些垂直线段是相等的。
27.【答案】错误
【解析】解:1×1×5
=1×5
=5(m2),
所以做一个棱长为1m的无盖正方体铁箱,至少需要铁皮5m2,即原题说法错误。
故答案为:错误。
【分析】正方体的表面积=棱长×棱长×6,本题中无盖正方体铁箱,所以只求5个面的面积,即棱长×棱长×5,计算即可得出答案。
28.【答案】正确
【解析】解:A×1.9=B×2.8,因为1.9<2.8,所以A>B。原题说法正确。
故答案为:正确。
【分析】积相等,一个因数较小的,另一个因数就较大。
29.【答案】错误
【解析】解:杠杆原理:动力×动力臂=阻力×阻力臂,根据杠杆原理可以确定杠杆原理背后隐藏着数学原理是反比例关系。
故答案为:错误。
【分析】两种相关联的量,若其比值一定,两种量成正比例关系;若其乘积一定,两种量成反比例关系。
30.【答案】正确
【解析】解:这块巧克力的单价最大可能是6.49元。
故答案为:错误。
【分析】把一个小数保留整数,就是把这个小数十分位上的数进行四舍五入即可。
31.【答案】错误
【解析】解:抛一枚硬币,如果抛10次,那么结果可能是5次正面朝上,5次反面朝上,原题干说法错误。
故答案为:错误。
【分析】抛一枚硬币,有正反两面,任意抛一次,两种情况都有可能发生,所以如果抛10次,那么结果可能是5次正面朝上,5次反面朝上;还可能是其它情况。
32.【答案】错误
33.【答案】错误
【解析】
近似数4.2与4.20的大小相等,精确的程度不相同,本题错。
故答案为:错误。
【分析】4.2精确到十分位,4.20精确到百分位。
34.【答案】+30%=0.9 3.2-=2.3 0.8÷= ×80%=0.5
÷= 3.6:= 3.14×42=50.24 ×90%÷×90%=0.81
【解析】含百分数的计算,把百分数化成分数或小数,然后再计算;求比值,用比的前项除以比的后项;分数、百分数乘除混合运算,按照从左到右的顺序计算。
35.【答案】解: ()×21
=×21+×21
=7+12
=19
=××
=×
=
=×(5+2+3)
=×10
=
【解析】观察数据可知,此题应用乘法分配律简算;
观察数据可知,此题应用乘法交换律和结合律,可以使计算简便;
观察数据可知,此题应用乘法分配律简算。
36.【答案】
解:
解:
解:1.2x=5×0.1
1.2x=0.5
x=
【解析】等式的基本性质1:等式两边同时加上或减去同一个数,等式仍然成立;等式的基本性质2:等式两边同时乘或除以同一个不为0的整式,等式仍然成立。
比例的基本性质:两个内项的积等于两个外项的积。
(1)先将百分数化为分数,得到,然后计算等式左边得到,最后根据等式的基本性质2,将等式两边同时除以,即可得到答案;
(2)先计算等式左边的除法,得到,再根据等式的基本性质2,将等式两边同时除以,即可得到答案;
(3)先根据比例的基本性质,得到1.2x=50.1,然后计算等式右边的小数乘法,得到1.2x=0.5,再根据等式的基本性质2,将等式两边同时除以1.2,即可得到答案。
37.【答案】(1)解:5×5÷2=12.5(cm2)
(2)解:(6-3+6)×3÷2= 13.5(cm2)
【解析】(1)观察图形,下半部分的阴影与上半部分的半圆形阴影可以拼成一个完整的长方形,占正方形面积的一半;计算出正方形面积再除以2即可。
(2)将右边扇形中的阴影部分移动到半圆形的左半边,发现刚好可以与长方形中的阴影部分拼成一个直角梯形;由于圆的半径是固定的,可知梯形的上底为6-3;利用梯形面积公式,代入数值计算即可。
38.【答案】(1)(6,4);(9,4);(4,1)
(2)解:如图所示:
【解析】用数对表示位置时,前面一个数表示第几列,后面一个数表示第几行;列数一般从左往右数,行数一般从前往后数;作平移图形的方法:先确定要平移图形的关键点,确定平移的方向是朝哪移的,然后确定移动的长度(格子数),最后把各点连接成图。
39.【答案】解:设原计划每小时生产x个零件,
依题意得:13x=12(x+10)-60,
解得:x=60.
答:原计划每小时生产60个零件.
【解析】设原计划每小时生产x个零件,根据每小时多生产10件,用了12小时不但完成任务,而且还多生产60件,原计划13小时生产的零件数=实际12小时生产的零件-60,列出方程,求解即可.
40.【答案】(1)790元
(2)买5组“买五送一”,需要付650元
41.【答案】解:50×2+141×3
=100+423
=523(千米)
答:李红家到南宁一共有523千米。
【解析】李红家到南宁一共的路程=汽车的速度×汽车行驶的时间+动车的速度×动车行驶的时间。
42.【答案】337.5块
43.【答案】解:方案一:5×20+45×4
=100+180
=280(元)
方案二:5+45=50(人)
50×5=250(元)
答:5位老师买成人票,45名学生买学生票,应付280元;买50张团体票,应付250元。
【解析】方案一总价=成人的人数×成人票单价+学生人数×学生票单价;方案二总价=(成人的人数+学生人数)×团体票单价。
44.【答案】解:设在摄氏x度时,华氏度的值恰好比摄氏度的值大60,可得,
答:在摄氏35度时,华氏度的值恰好比摄氏度的值大60
【解析】设在摄氏x℃时,华氏度的值恰好比摄氏度的值大60。
根据题目给出的换算公式,可以列出方程:,然后解方程即可
45.【答案】解:3150÷(7-4)
=3150÷3
=1050(元)
答:平均每台洗衣机售价1050元。
【解析】上午比下午收货款少,是因为上午比下午少卖了(7-4)台,用少收的货款数除以少卖的台数即可求出平均每台的售价。
46.【答案】解:甲、乙两个旅游团购买了:117×(1-)=13(份)
每份水席套餐团购价:250×(1-)=200(元)
甲旅游团应付:13××200=1400(元)
乙旅游团应付: 13××200=1200(元)
答:甲旅游团应付1400元,乙旅游团应付 1200 元。
【解析】求卖了一后剩余水席套餐的份数和团购价格,再求将这剩余的水席套餐卖给甲、乙两个旅游团各多少份,再乘以团购价即可。
47.【答案】解:1.6米=16分米,70厘米=7分米。
披肩面积16×7÷2=56(平方分米),
需要金额:56÷4=14(元),
答:奶奶们每人需要花费14元。
【解析】 本题考查了三角形面积公式在实际生活中的应用以及单位换算。先根据面积公式底×高÷2求出披肩的面积,再根据布料价格求出所需费用,解题过程中要注意单位的统一,将米和厘米都换算成分米,方便计算。
48.【答案】解:客车:
=160×
=100(千米)
货车:480÷3-100=60(千米)
答:客车每小时行100千米,货车每小时行60千米。
【解析】用两地的距离除以相遇时间求出速度和,然后把速度和按照5:3的比分配后分别求出客车和货车每小时分别行的路程。
21世纪教育网(www.21cnjy.com)
同课章节目录
