2023-2024学年辽宁省铁岭五中七年级(下)期末数学试卷(含答案)
文档属性
| 名称 | 2023-2024学年辽宁省铁岭五中七年级(下)期末数学试卷(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 264.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 21:52:56 | ||
图片预览




文档简介
2023-2024学年辽宁省铁岭五中七年级(下)期末数学试卷
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.皮影戏是中国民间古老的传统艺术,年中国皮影戏人选人类非物质文化遗产代表作名录,平移如图所示的孙悟空皮影造型,能得到下列图中的( )
A. B. C. D.
2.为了解某市参加中考的名学生的身高情况,抽查了其中名学生的身高进行统计分析下面叙述正确的是( )
A. 名学生是总体 B. 名学生的身高是总体的一个样本
C. 每名学生是总体的一个个体 D. 以上调查是全面调查
3.下列命题是真命题的是( )
A. 和为的两个角是邻补角
B. 一条直线的垂线有且只有一条
C. 点到直线的距离是指这点到直线的垂线段
D. 两条直线被第三条直线所截,如内错角相等,则同位角必相等
4.若关于的不等式组,有且只有个整数解,且关于的一元一次方程的解是正整数,则所有满足条件的整数的值之和为( )
A. B. C. D.
5.下列说法中,错误的是( )
与相交,与相交,则与相交;
若,,则;
过直线外一点有且只有一条直线与已知直线平行;
在同一平面内,两条直线的位置关系平行、相交、垂直三种.
A. 个 B. 个 C. 个 D. 个
6.若是整数,则正整数不可能是( )
A. B. C. D.
7.已知,,则的值为( )
A. 或 B. 或 C. 或 D. 、 或
8.生态园位于县城东北方向公里处,如图表示准确的是( )
A. B.
C. D.
9.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走,平路每小时走下坡每小时走,那么从甲地到乙地需,从乙地到甲地需设从甲地到乙地的上坡路程长,平路路程长为,依题意列方程组正确的是( )
A. B. C. D.
10.如图,,点为上方一点,,分别为,的角平分线,若,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.把图中的长方形分割成,两个小长方形,按如图所示拼接恰好组成一个大正方形空余部分是正方形若拼接后的大正方形的面积为,则图中原长方形的周长为______.
12.若,则与的关系是______.
13.若是关于,的二元一次方程,则的值______.
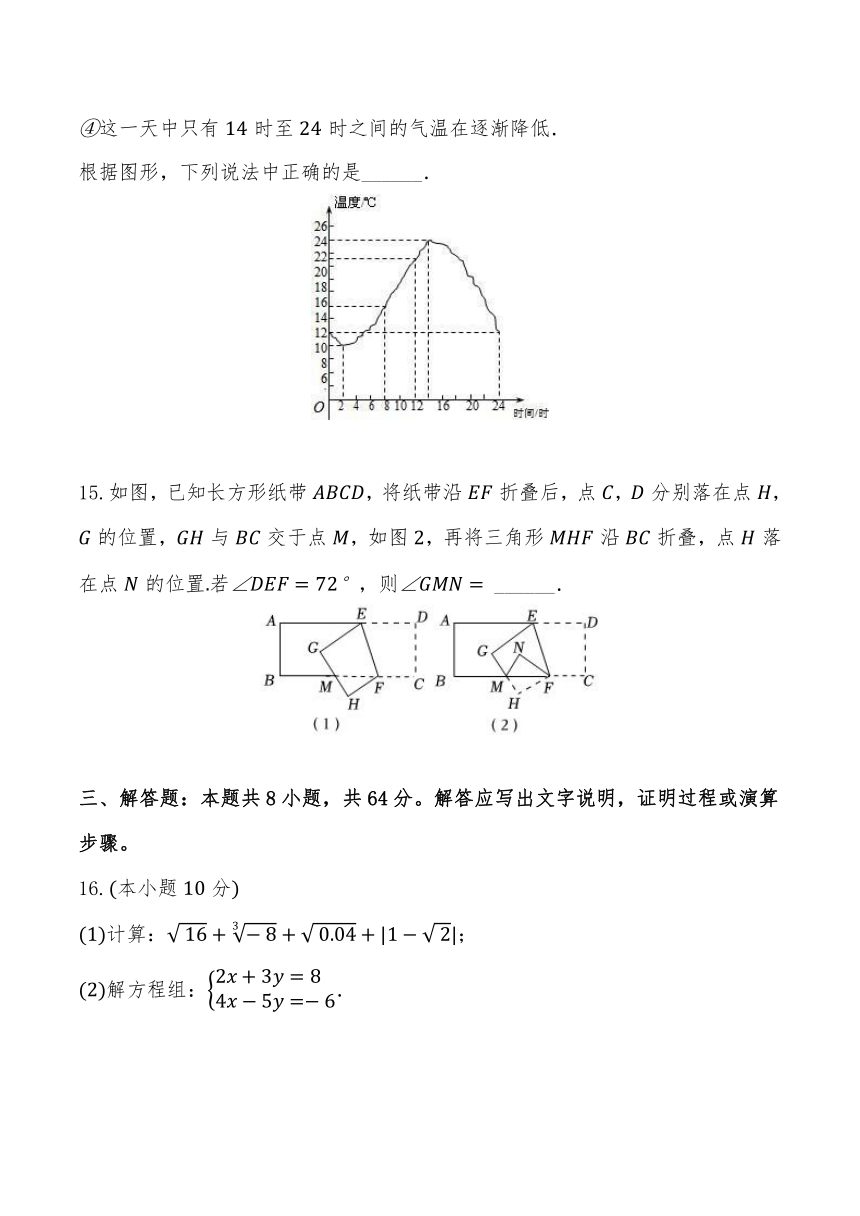
14.如图是我市某一天内的气温变化图:
这一天中最高气温是;
这一天中最高气温与最低气温的差为;
这一天中时至时之间的气温在逐渐升高;
这一天中只有时至时之间的气温在逐渐降低.
根据图形,下列说法中正确的是______.
15.如图,已知长方形纸带,将纸带沿折叠后,点,分别落在点,的位置,与交于点,如图,再将三角形沿折叠,点落在点的位置若,则 ______.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
解方程组:.
17.本小题分
已知关于,的方程组.
若方程组的解满足,求的值.
无论实数取何值,关于,的方程总有一个固定的解,请求出这个解.
18.本小题分
已知与在平面直角坐标系中的位置如图所示.
分别写出下列各点的坐标:
______; ______; ______;
若点是内部一点,则点在内部的对应点的坐标为______;
求的面积.
本小题分
某校为提高学生的综合素质,准备开设“泥塑”“绘画”“书法”“街舞”四门校本课程,为了解学生对这四门课程的选择情况要求每名学生只能选择其中一门课程,学校从七年级学生中随机抽取部分学生进行问卷调查,根据调查结果绘制成如图所示的两幅不完整的统计图,请你依据图中信息解答下列问题:
参加此次问卷调查的学生人数是______人,在扇形统计图中,选择“泥塑”的学生所对应的扇形圆心角的度数是______;
通过计算将条形统计图补充完整;
若该校七年级共有名学生,请估计七年级学生中选择“书法”课程的约有多少人?
20.本小题分
原创题如图所示,在内有一点.
过画;过画;
用量角器量一量与相交的角与的大小有怎样关系?
21.本小题分
为提高业主垃圾分类的意识,某小区物业决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买个提示牌和个垃圾箱共需要元,购买个提示牌和个垃圾箱共需要元.
问提示牌和垃圾箱的单价各是多少元;
如果需要购买提示牌和垃圾箱共个,且费用不超过元,问该小区最多可以购买多少个垃圾箱?
22.本小题12分
如图,.
求证:;
若平分,,,求的度数.
23.本小题分
【探究】
如图,若,点在,外部,则,,满足的数量关系是______;
【应用】
如图为北斗七星的位置图,如图,将北斗七星分别标为,,,,,,其中,三点在一条直线上,,则,,满足的数量关系是______
如图,在问的条件下,延长到点,延长到点,过点和点分别作射线和交于点,使得平分,平分,若,直接写出的度数.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.互为相反数
13.
14.
15.
16.解:
;
,
得:,
得:,
解得:,
把代入得:,
解得:,
故原方程组的解是:.
17.解:方程组的解满足,
,
得:,
把代入得:,
方程组的解为:,
把代入得:
,
,
;
无论实数取何值,关于,的方程总有一个固定的解,
方程的解与的值无关,
,
,
,即时,,
关于,的方程的解为:.
18.解:; ;;
;
的面积
.
19.,;
“绘画”的人数为:人,
补全条形统计图如图所示.
名.
答:七年级学生中选择“书法”课程的约有人.
20.解:如图所示,
与夹角有两个:,;,,
所以和的夹角与相等或互补.
21.解:设提示牌的单价是元,垃圾箱的单价是元,
,
解得,
答:提示牌的单价是元,垃圾箱的单价是元;
设购买垃圾箱个,则购买提示牌个,
费用不超过元,
,
解得,
为正整数,
的最大值为,
答:该小区最多可购买个垃圾箱.
22.证明:,,
,
;
解:,
,
又,
,
,
,,
平分,
,
.
23.解:【探究】过点作,如图所示:
,
,
,,
,,
,
,
【应用】过点作,如图所示:
,
,
,,
,
,
,
,
,理由如下:
过点作,如图所示:
,平分,
,,
平分,
设,则,
在的条件下:
,
,
,
,,
,
,,
,
,
.
【探究】过点作,则,进而得,,再根据即可得出,,满足的数量关系;
一、选择题:本题共10小题,每小题3分,共30分。在每小题给出的选项中,只有一项是符合题目要求的。
1.皮影戏是中国民间古老的传统艺术,年中国皮影戏人选人类非物质文化遗产代表作名录,平移如图所示的孙悟空皮影造型,能得到下列图中的( )
A. B. C. D.
2.为了解某市参加中考的名学生的身高情况,抽查了其中名学生的身高进行统计分析下面叙述正确的是( )
A. 名学生是总体 B. 名学生的身高是总体的一个样本
C. 每名学生是总体的一个个体 D. 以上调查是全面调查
3.下列命题是真命题的是( )
A. 和为的两个角是邻补角
B. 一条直线的垂线有且只有一条
C. 点到直线的距离是指这点到直线的垂线段
D. 两条直线被第三条直线所截,如内错角相等,则同位角必相等
4.若关于的不等式组,有且只有个整数解,且关于的一元一次方程的解是正整数,则所有满足条件的整数的值之和为( )
A. B. C. D.
5.下列说法中,错误的是( )
与相交,与相交,则与相交;
若,,则;
过直线外一点有且只有一条直线与已知直线平行;
在同一平面内,两条直线的位置关系平行、相交、垂直三种.
A. 个 B. 个 C. 个 D. 个
6.若是整数,则正整数不可能是( )
A. B. C. D.
7.已知,,则的值为( )
A. 或 B. 或 C. 或 D. 、 或
8.生态园位于县城东北方向公里处,如图表示准确的是( )
A. B.
C. D.
9.从甲地到乙地有一段上坡与一段平路,如果保持上坡每小时走,平路每小时走下坡每小时走,那么从甲地到乙地需,从乙地到甲地需设从甲地到乙地的上坡路程长,平路路程长为,依题意列方程组正确的是( )
A. B. C. D.
10.如图,,点为上方一点,,分别为,的角平分线,若,则的度数为( )
A.
B.
C.
D.
二、填空题:本题共5小题,每小题3分,共15分。
11.把图中的长方形分割成,两个小长方形,按如图所示拼接恰好组成一个大正方形空余部分是正方形若拼接后的大正方形的面积为,则图中原长方形的周长为______.
12.若,则与的关系是______.
13.若是关于,的二元一次方程,则的值______.
14.如图是我市某一天内的气温变化图:
这一天中最高气温是;
这一天中最高气温与最低气温的差为;
这一天中时至时之间的气温在逐渐升高;
这一天中只有时至时之间的气温在逐渐降低.
根据图形,下列说法中正确的是______.
15.如图,已知长方形纸带,将纸带沿折叠后,点,分别落在点,的位置,与交于点,如图,再将三角形沿折叠,点落在点的位置若,则 ______.
三、解答题:本题共8小题,共64分。解答应写出文字说明,证明过程或演算步骤。
16.本小题分
计算:;
解方程组:.
17.本小题分
已知关于,的方程组.
若方程组的解满足,求的值.
无论实数取何值,关于,的方程总有一个固定的解,请求出这个解.
18.本小题分
已知与在平面直角坐标系中的位置如图所示.
分别写出下列各点的坐标:
______; ______; ______;
若点是内部一点,则点在内部的对应点的坐标为______;
求的面积.
本小题分
某校为提高学生的综合素质,准备开设“泥塑”“绘画”“书法”“街舞”四门校本课程,为了解学生对这四门课程的选择情况要求每名学生只能选择其中一门课程,学校从七年级学生中随机抽取部分学生进行问卷调查,根据调查结果绘制成如图所示的两幅不完整的统计图,请你依据图中信息解答下列问题:
参加此次问卷调查的学生人数是______人,在扇形统计图中,选择“泥塑”的学生所对应的扇形圆心角的度数是______;
通过计算将条形统计图补充完整;
若该校七年级共有名学生,请估计七年级学生中选择“书法”课程的约有多少人?
20.本小题分
原创题如图所示,在内有一点.
过画;过画;
用量角器量一量与相交的角与的大小有怎样关系?
21.本小题分
为提高业主垃圾分类的意识,某小区物业决定在小区内安装垃圾分类的提示牌和垃圾箱,若购买个提示牌和个垃圾箱共需要元,购买个提示牌和个垃圾箱共需要元.
问提示牌和垃圾箱的单价各是多少元;
如果需要购买提示牌和垃圾箱共个,且费用不超过元,问该小区最多可以购买多少个垃圾箱?
22.本小题12分
如图,.
求证:;
若平分,,,求的度数.
23.本小题分
【探究】
如图,若,点在,外部,则,,满足的数量关系是______;
【应用】
如图为北斗七星的位置图,如图,将北斗七星分别标为,,,,,,其中,三点在一条直线上,,则,,满足的数量关系是______
如图,在问的条件下,延长到点,延长到点,过点和点分别作射线和交于点,使得平分,平分,若,直接写出的度数.
1. 2. 3. 4. 5. 6. 7. 8. 9. 10.
11.
12.互为相反数
13.
14.
15.
16.解:
;
,
得:,
得:,
解得:,
把代入得:,
解得:,
故原方程组的解是:.
17.解:方程组的解满足,
,
得:,
把代入得:,
方程组的解为:,
把代入得:
,
,
;
无论实数取何值,关于,的方程总有一个固定的解,
方程的解与的值无关,
,
,
,即时,,
关于,的方程的解为:.
18.解:; ;;
;
的面积
.
19.,;
“绘画”的人数为:人,
补全条形统计图如图所示.
名.
答:七年级学生中选择“书法”课程的约有人.
20.解:如图所示,
与夹角有两个:,;,,
所以和的夹角与相等或互补.
21.解:设提示牌的单价是元,垃圾箱的单价是元,
,
解得,
答:提示牌的单价是元,垃圾箱的单价是元;
设购买垃圾箱个,则购买提示牌个,
费用不超过元,
,
解得,
为正整数,
的最大值为,
答:该小区最多可购买个垃圾箱.
22.证明:,,
,
;
解:,
,
又,
,
,
,,
平分,
,
.
23.解:【探究】过点作,如图所示:
,
,
,,
,,
,
,
【应用】过点作,如图所示:
,
,
,,
,
,
,
,
,理由如下:
过点作,如图所示:
,平分,
,,
平分,
设,则,
在的条件下:
,
,
,
,,
,
,,
,
,
.
【探究】过点作,则,进而得,,再根据即可得出,,满足的数量关系;
同课章节目录
