江苏省如皋市09-10学年高一上学期期中调研测试(数学)
文档属性
| 名称 | 江苏省如皋市09-10学年高一上学期期中调研测试(数学) |  | |
| 格式 | zip | ||
| 文件大小 | 169.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-02-27 22:10:00 | ||
图片预览




文档简介
如皋市09-10学年高一上学期期中调研测试
数学
一 填空题:本大题共14小题,每小题5分,共70分,不需写出解答过程,请把答案直接填写在答题纸相应位置上.
1.集合,若,则的值为__ ___.
2. 已知,且是第二象限角,则的值为_ ______.
3. 已知全集,集合,则=____ ___.
4. 已知幂函数的图象过点,则= .
5. 已知扇形的周长为,面积为,则扇形圆心角的弧度数为_________.
6.函数的定义域为 _____________.
7. 下列4个命题,其中命题正确的有_ _.
①函数是其定义域到值域的映射;
②是函数;
③函数的图象是一条直线;
④函数的图象与直线图象最多只有一个公共点.
8. 定义在实数集上的偶函数在区间上是单调增函数,若,则的取值范围是__ ____.
9.已知,求的值为__ ____.
10. 设方程的解为,则关于的不等式的最大整数解为____ .
11. 已知的对应关系如下表,则的对应关系的一个表达式可以为 .
1 2 3 4 5
3 8 15 24 35
12.设函数则不等式的解集是______ ____.
13.已知函数的值域为,则实数的值为__ ____.
14.已知函数,分别由下表给出
1 2 3 5
3 2 3 2
1 2 3 4
1 3 1 3
满足的的值是 .
二.解答题:本大题共6小题,共90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15. (本题满分14分)
已知,求的值.
16. (本题满分14分)
已知函数是奇函数.
求的值;
写出的单调区间(不需要证明);
求的值域.
17. (本题满分15分)函数的图象与函数的图象交于两点(在线段 上,为坐标原点),过作轴的垂线,垂足分别为,并且分别交函数的图象于两点.
(1)试探究线段的关系;
(2)若平行于轴,求四边形的面积.
18. (本题满分15分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元
(2)当一次订购量为个, 每件商品的实际批发价为元,写出函数的表达式;
(3)根据市场调查发现,经销商一次最大定购量为个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
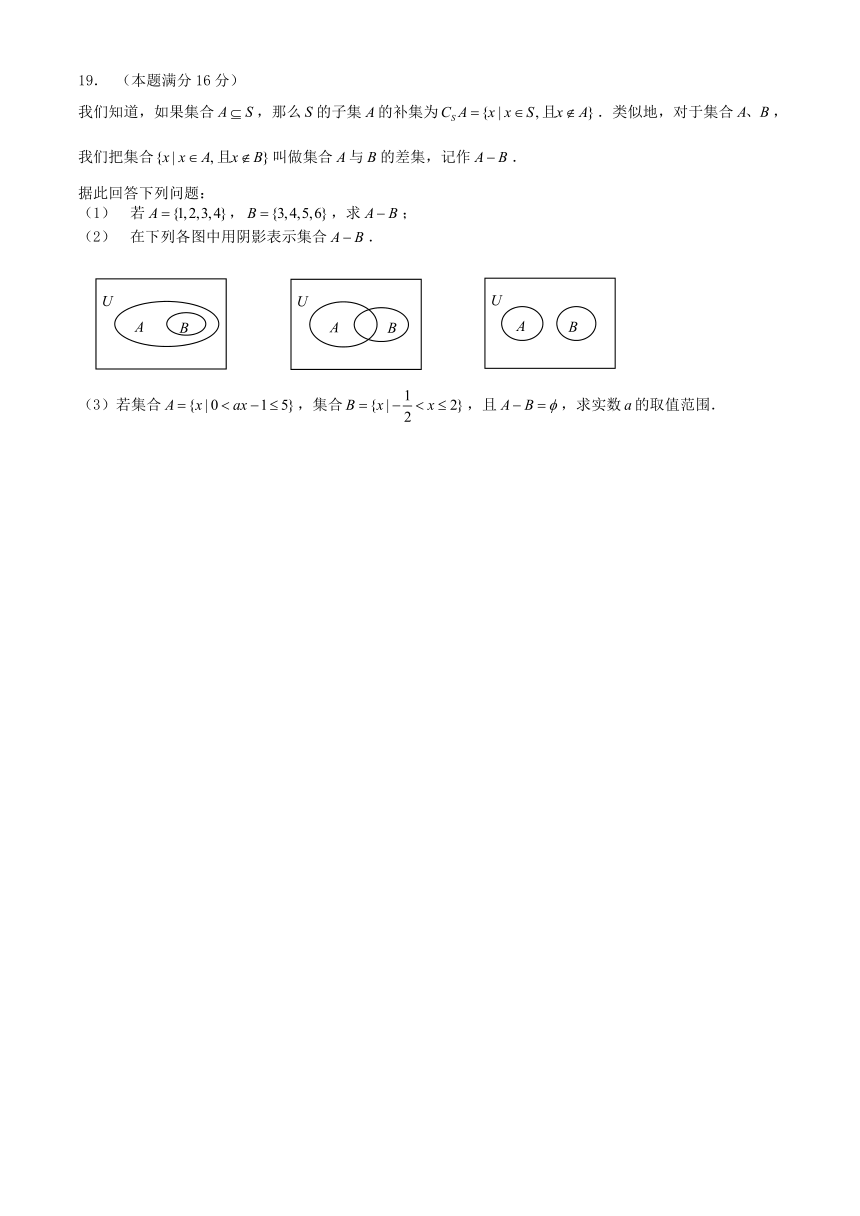
19. (本题满分16分)
我们知道,如果集合,那么的子集的补集为.类似地,对于集合,我们把集合叫做集合与的差集,记作.
据此回答下列问题:
若,,求;
在下列各图中用阴影表示集合.
(3)若集合,集合,且,求实数的取值范围.
20. (本题满分16分)
已知二次函数对于任意的实数,
都有成立,且为偶函数.
(1)求的取值范围;
(2)求函数在上的值域;
(3)定义区间的长度为.是否存在常数,使的函数在区间的值域为,且的长度为.
如皋市09-10学年高一上学期期中调研测试
高一数学答案
一 填空题:本大题共14小题,每小题5分,共70分,不需写出解答过程,请把答案直接填写在答题纸相应位置上.
1.集合,若,则的值为__4___.
2. 已知,且是第二象限角,则的值为_______.
3. 已知全集,集合,则=_______
4. 已知幂函数的图象过点,则=
5. 已知扇形的周长为,面积为,则扇形圆心角的弧度数为_________.
6.函数的定义域为 _____________.
7. 下列4个命题,其中命题正确的有_①_④_
①函数是其定义域到值域的映射;
②是函数;
③函数的图象是一条直线;
④函数的图象与直线图象最多只有一个公共点.
8. 定义在实数集上的偶函数在区间上是单调增函数,若,则的取值范围是______.
9.已知,求的值为______.
10. 设方程的解为,则关于的不等式的最大整数解为_2_____.
11. 已知的对应关系如下表,则的对应关系的一个表达式可以为 .
1 2 3 4 5
3 8 15 24 35
12.设函数则不等式的解集是__________.
13.已知函数的值域为,则实数的值为______.
14.已知函数,分别由下表给出
1 2 3 5
3 2 3 2
1 2 3 4
1 3 1 3
满足的的值是 2 .
二.解答题:本大题共6小题,共90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15. (本题满分14分)
已知,求的值
解:由得,则. 6分
= 10分
= 14分
16. (本题满分14分)
已知函数是奇函数.
求的值;
写出的单调区间(不需要证明);
求的值域.
略解:(1) 5分
在上分别递减;上递增; 9分
. 14分
17. (本题满分15分)函数的图象与函数的图象交于两点(在线段 上,为坐标原点),过作轴的垂线,垂足分别为,并且分别交函数的图象于两点.
(1)试探究线段的关系;
(2)若平行于轴,求四边形的面积.
解:由题意可设,则
(1),
故; 7分
(2)若平行于轴,则;又
联立方程组解得
此时,,所以四边形的面积=. 15分
18. (本题满分15分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元
(2)当一次订购量为个, 每件商品的实际批发价为元,写出函数的表达式;
(3)根据市场调查发现,经销商一次最大定购量为个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
解:(1)设一次订购量为,
则批发价为,令,,
所以当一次订购量为550个时,每件商品的实际批发价为102元. 5分
(2)由题意知 10分
(3)当经销商一次批发个零件时,该批发公司可获得利润为,根据题意知:
设,在时,取得最大值为;
设
所以当时,取最大值.
答:当经销商一次批发500个零件时,该批发公司可获得最大利润. 15分
19. (本题满分16分)
我们知道,如果集合,那么的子集的补集为.类似地,对于集合,我们把集合叫做集合与的差集,记作.
据此回答下列问题:
若,,求;
在下列各图中用阴影表示集合.
(3)若集合,集合,且,求实数的取值范围.
解:(1)=; 5分
(2)
10分
(3),则,
当时,,此时,符号题意;
当时,,若,则;
当时,,若,则;
综上所述:实数的取值范围是或. 16分
20. (本题满分16分)
已知二次函数对于任意的实数,
都有成立,且为偶函数.
(1)求的取值范围;
(2)求函数在上的值域;
(3)定义区间的长度为.是否存在常数,使的函数在区间的值域为,且的长度为.
解析:
由为偶函数可得的图像关于直线对称,
则,;
对于任意的实数,都有成立,则
=
因为,所以故. 5分
(2),因为,所以.
当时,即时,
函数的值域为;
当时,
函数的值域为;
当时,
函数的值域为. 10分
(3),
当时,
由时,则而,不合题意;
当时,
由,得,所以,不合题意;
当时,
故因为,所以.
综上所述:存在常数符合题意. 16分
www.
B
A
U
B
A
U
B
A
U
B
A
U
B
A
U
B
A
U
A
U
B
数学
一 填空题:本大题共14小题,每小题5分,共70分,不需写出解答过程,请把答案直接填写在答题纸相应位置上.
1.集合,若,则的值为__ ___.
2. 已知,且是第二象限角,则的值为_ ______.
3. 已知全集,集合,则=____ ___.
4. 已知幂函数的图象过点,则= .
5. 已知扇形的周长为,面积为,则扇形圆心角的弧度数为_________.
6.函数的定义域为 _____________.
7. 下列4个命题,其中命题正确的有_ _.
①函数是其定义域到值域的映射;
②是函数;
③函数的图象是一条直线;
④函数的图象与直线图象最多只有一个公共点.
8. 定义在实数集上的偶函数在区间上是单调增函数,若,则的取值范围是__ ____.
9.已知,求的值为__ ____.
10. 设方程的解为,则关于的不等式的最大整数解为____ .
11. 已知的对应关系如下表,则的对应关系的一个表达式可以为 .
1 2 3 4 5
3 8 15 24 35
12.设函数则不等式的解集是______ ____.
13.已知函数的值域为,则实数的值为__ ____.
14.已知函数,分别由下表给出
1 2 3 5
3 2 3 2
1 2 3 4
1 3 1 3
满足的的值是 .
二.解答题:本大题共6小题,共90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15. (本题满分14分)
已知,求的值.
16. (本题满分14分)
已知函数是奇函数.
求的值;
写出的单调区间(不需要证明);
求的值域.
17. (本题满分15分)函数的图象与函数的图象交于两点(在线段 上,为坐标原点),过作轴的垂线,垂足分别为,并且分别交函数的图象于两点.
(1)试探究线段的关系;
(2)若平行于轴,求四边形的面积.
18. (本题满分15分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元
(2)当一次订购量为个, 每件商品的实际批发价为元,写出函数的表达式;
(3)根据市场调查发现,经销商一次最大定购量为个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
19. (本题满分16分)
我们知道,如果集合,那么的子集的补集为.类似地,对于集合,我们把集合叫做集合与的差集,记作.
据此回答下列问题:
若,,求;
在下列各图中用阴影表示集合.
(3)若集合,集合,且,求实数的取值范围.
20. (本题满分16分)
已知二次函数对于任意的实数,
都有成立,且为偶函数.
(1)求的取值范围;
(2)求函数在上的值域;
(3)定义区间的长度为.是否存在常数,使的函数在区间的值域为,且的长度为.
如皋市09-10学年高一上学期期中调研测试
高一数学答案
一 填空题:本大题共14小题,每小题5分,共70分,不需写出解答过程,请把答案直接填写在答题纸相应位置上.
1.集合,若,则的值为__4___.
2. 已知,且是第二象限角,则的值为_______.
3. 已知全集,集合,则=_______
4. 已知幂函数的图象过点,则=
5. 已知扇形的周长为,面积为,则扇形圆心角的弧度数为_________.
6.函数的定义域为 _____________.
7. 下列4个命题,其中命题正确的有_①_④_
①函数是其定义域到值域的映射;
②是函数;
③函数的图象是一条直线;
④函数的图象与直线图象最多只有一个公共点.
8. 定义在实数集上的偶函数在区间上是单调增函数,若,则的取值范围是______.
9.已知,求的值为______.
10. 设方程的解为,则关于的不等式的最大整数解为_2_____.
11. 已知的对应关系如下表,则的对应关系的一个表达式可以为 .
1 2 3 4 5
3 8 15 24 35
12.设函数则不等式的解集是__________.
13.已知函数的值域为,则实数的值为______.
14.已知函数,分别由下表给出
1 2 3 5
3 2 3 2
1 2 3 4
1 3 1 3
满足的的值是 2 .
二.解答题:本大题共6小题,共90分,请在答题纸指定区域内作答,解答时应写出文字说明、证明过程或演算步骤.
15. (本题满分14分)
已知,求的值
解:由得,则. 6分
= 10分
= 14分
16. (本题满分14分)
已知函数是奇函数.
求的值;
写出的单调区间(不需要证明);
求的值域.
略解:(1) 5分
在上分别递减;上递增; 9分
. 14分
17. (本题满分15分)函数的图象与函数的图象交于两点(在线段 上,为坐标原点),过作轴的垂线,垂足分别为,并且分别交函数的图象于两点.
(1)试探究线段的关系;
(2)若平行于轴,求四边形的面积.
解:由题意可设,则
(1),
故; 7分
(2)若平行于轴,则;又
联立方程组解得
此时,,所以四边形的面积=. 15分
18. (本题满分15分)某批发公司批发某商品,每件商品进价80元,批发价120元,该批发商为鼓励经销商批发,决定当一次批发量超过100个时,每多批发一个,批发的全部商品的单价就降低0.04元,但最低批发价不能低于102元.
(1)当一次订购量为多少个时,每件商品的实际批发价为102元
(2)当一次订购量为个, 每件商品的实际批发价为元,写出函数的表达式;
(3)根据市场调查发现,经销商一次最大定购量为个,则当经销商一次批发多少个零件时,该批发公司可获得最大利润.
解:(1)设一次订购量为,
则批发价为,令,,
所以当一次订购量为550个时,每件商品的实际批发价为102元. 5分
(2)由题意知 10分
(3)当经销商一次批发个零件时,该批发公司可获得利润为,根据题意知:
设,在时,取得最大值为;
设
所以当时,取最大值.
答:当经销商一次批发500个零件时,该批发公司可获得最大利润. 15分
19. (本题满分16分)
我们知道,如果集合,那么的子集的补集为.类似地,对于集合,我们把集合叫做集合与的差集,记作.
据此回答下列问题:
若,,求;
在下列各图中用阴影表示集合.
(3)若集合,集合,且,求实数的取值范围.
解:(1)=; 5分
(2)
10分
(3),则,
当时,,此时,符号题意;
当时,,若,则;
当时,,若,则;
综上所述:实数的取值范围是或. 16分
20. (本题满分16分)
已知二次函数对于任意的实数,
都有成立,且为偶函数.
(1)求的取值范围;
(2)求函数在上的值域;
(3)定义区间的长度为.是否存在常数,使的函数在区间的值域为,且的长度为.
解析:
由为偶函数可得的图像关于直线对称,
则,;
对于任意的实数,都有成立,则
=
因为,所以故. 5分
(2),因为,所以.
当时,即时,
函数的值域为;
当时,
函数的值域为;
当时,
函数的值域为. 10分
(3),
当时,
由时,则而,不合题意;
当时,
由,得,所以,不合题意;
当时,
故因为,所以.
综上所述:存在常数符合题意. 16分
www.
B
A
U
B
A
U
B
A
U
B
A
U
B
A
U
B
A
U
A
U
B
同课章节目录
