浙江省杭州市二中2024-2025学年下学期高一6月统测数学试卷(图片版,含答案)
文档属性
| 名称 | 浙江省杭州市二中2024-2025学年下学期高一6月统测数学试卷(图片版,含答案) |

|
|
| 格式 | |||
| 文件大小 | 849.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 00:00:00 | ||
图片预览




文档简介
2025杭州二中 6月统测
★祝大家学习生活愉快★
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号,试室号,座位号填写在答题
卡上。用 2B铅笔将试卷类型和考生号填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应的题目选项的答案信息点涂黑;如需改动,用
橡皮擦干净后,再填涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置
上;如需改动,先划掉原来的答案,然后再写上新的答案,不准使用铅笔和涂改液。不按以上要求作答的答
案无效。
一、单选题:本题共 8小题,每小题 5分,共 40分,每小题只有一个选项符合要求
1.设集合A= 3,4,5 ,B= 2,3,4,8 ,则图中阴影部分表示的集合为 ( )
A. 2,8 B. 3,4
C. 2,5,8 D. 3,4,5
2. “ac= bc”是“a= b”的 ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
3.在某次全市高三模拟考试后,数学老师随机抽取了 6名同学的第一个解答题的得分情况如下:7,10,5,
8,4,2,则这组数据的平均数和 30%分位数分别为 ( )
A. 6,3 B. 5,3 C. 5,4 D. 6,4
4.在三棱锥P-ABC中,PA=BC= 10,PB=AC= 5,PC=AB= 13,则该三棱锥的外接球的表
面积为 ( )
A. 28π B. 28 73 π C. 7π D. 14π
5.在平面直角坐标系 xOy中,角 α与角 β均以 x轴的非负半轴为始边,它们的终边关于直线 y=-x对称.
3
若角 α的终边与单位圆交点P的纵坐标为 5 ,则 cosβ= ( )
A. 3 B. - 3 C. 45 5 5 D. -
4
5
6.Deepseek(深度求索)是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点.在神经网络
G
优化中,指数衰减的学习率模型为 L=L DG00 ,其中L表示每一轮优化时使用的学习率,L0表示初始学习
率,D表示衰减系数,G表示训练迭代轮数,G0表示衰减速度.已知某个指数衰减的学习率模型的初始
学习率 L0为 0.6,衰减速度G0为 20,且当训练迭代轮数为 10时,学习率衰减为 0.3,则学习率衰减到 0.2
以下 (不含 0.2)所需的训练迭代轮数至少为 ( )
(参考数据:lg2≈ 0.3,lg3≈ 0.477)
A. 14 B. 15 C. 16 D. 17
数学试题 第 1 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
2 2
7.已知函数 f x 1 = 2x+ x-1 的对称中心在直线 y= ax+ b a>0
a +2b
上,则 2a 的最小值为 ( )
A. 4 3- 4 B. 4 3+ 4 C. 2 6- 4 D. 2 6+ 4
8. 已知平面向量 a,b,c满足:a与 b的夹角为锐角, a = 2, b = 4, c = 1,且 t∈R, b+ta ≥ b-a ,
则 c -a c - 12 b 的最小值是 ( )
A. 0 B. 3+ 2 3 C. 6 D. 3- 2 3
二、多选题:本题共 3小题,每小题 6分,共 18分。在每小题给出的四个选项中,有多项符合题目要求。全
部选对的得 6分,部分选对的得部分分,有选错的得 0分。
9.已知事件A ,B,且P A = 0.4 ,P B = 0.5,则 ( )
A. 事件A与事件B互为对立事件 B. 若事件A与事件B互斥,则P A∪B = 0.9
C. 若事件A与事件B互斥,则P AB = 0.2 D. 若P AB = 0.3,则事件A与事件B相互独立
10.如图是一个棱长为 1的正方体的展开图,其中M,N分别为CH,DB的中点.如果将它还原成正方体,
那么下列选项中正确的是 ( )
A. π直线AB与CD所成角为 3
B. 直线EF与GH平行
C. 经过DEMN 9四个点的球的表面积为 4 π
D. P 7是正方形GKHI内的动点,若 |AP| = 2 ,那么 P点的轨迹长为
3
4 π
11.已知函数 f x = sinx+cos x sinx-cosx ,下列说法正确的是 ( )
A. f(x)的周期为 2π
B. f(x) π π在区间 - , 2 2 上是增函数
C. 若 f x1 + f x = 2 x + x = kπ 2 ,则 1 2 2 (k∈ Z)
D. 函数 g(x) = f(x) + 1在区间 [0 , 2π]上有且仅有 2个零点
三、填空题:本题共 3小题,每小题 5分,共 15分
12.在复数范围内,a a<0 的所有平方根为 .
13.某海警船在A处看灯塔B在它的北偏东 75°,距离为 3 6nmile,在A处看灯塔C
在海警船的北偏西 30°,距离为 2 3nmile,海警船由A处向正北航行到D处时,
再看灯塔B在南偏东 60°,则灯塔C与D处之间的距离为 nmile.
14.在三棱锥A-BCD中,AC⊥AB ,BD⊥AB,且AC=BD= 20 ,AB= 6,若三
棱锥A-BCD的外接球表面积的取值范围为 661π,1636π ,则三棱锥A-BCD
体积的取值范围为 .
数学试题 第 2 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
四、解答题:本题共 5小题,共 77分,解答应写出文字说明,证明过程或演算步骤
15. (13 ) e e a= 3e + e b=-2e + 2e c
分 已知 1, 2是平面内一对不共线的向量,且 1 2, 1 2, = λe1- 3e2.
(1) 2a - c
若 与 b+ 2c 共线,求实数 λ的值;
(2) c 若 = 12 a
+ μb,求 λ+ μ的值.
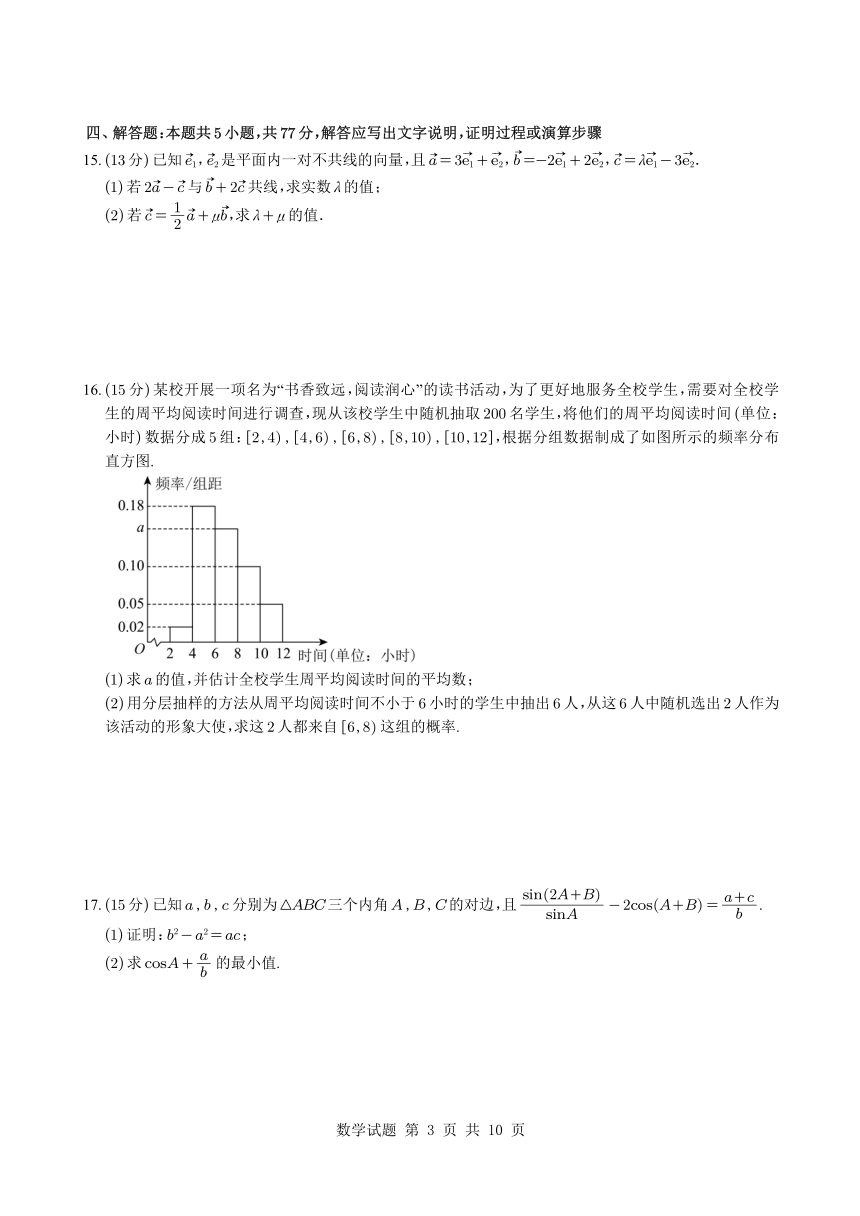
16. (15分)某校开展一项名为“书香致远,阅读润心”的读书活动,为了更好地服务全校学生,需要对全校学
生的周平均阅读时间进行调查,现从该校学生中随机抽取 200名学生,将他们的周平均阅读时间 (单位:
小时)数据分成 5组: 2,4 , 4,6 , 6,8 , 8,10 , 10,12 ,根据分组数据制成了如图所示的频率分布
直方图.
(1)求 a的值,并估计全校学生周平均阅读时间的平均数;
(2)用分层抽样的方法从周平均阅读时间不小于 6小时的学生中抽出 6人,从这 6人中随机选出 2人作为
该活动的形象大使,求这 2人都来自 6,8 这组的概率.
sin 2A+B
17. ( 15分)已知 a , b , c a+c分别为△ABC三个内角A ,B ,C的对边,且 - 2cos A+B = .
sinA b
(1)证明:b2- a2= ac;
(2) cosA+ a求 的最小值.
b
数学试题 第 3 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
18. (17分)如图 1,在平面五边形ABCDE中,∠EAC=∠DCA= π2 ,AE= 4,CD= 2,AB= BC=AC=
2 3,F ,H分别为ED ,AD的中点,将△ABC沿AC翻折,使点B到点P的位置,如图 2.
(1)若PH⊥平面ACDE.
(ⅰ)求异面直线PA与CF所成角的大小;
(ⅱ)三棱锥P-ACD的各顶点都在球O上,M为球O球面上的动点,求EM的取值范围.
(2)在翻折的过程中,设平面PCD与平面PAE的交线为 l,求二面角A- l-C的最小值.
19. (17分)已知函数 f x = x-a - 1 x + a , a∈R.
(1)若 f 1 ≤ 2,求 a的取值范围;
(2)若存在两个不相等的正实数 x1 , x2,满足 f x1 = f x2 .
(i)求 y= f x 在 x∈ 1,2 上的最小值;
(ii)证明:2< x1+ x2< 2a.
数学试题 第 4 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
参考答案
CBDDBCCD
BD ACD ACD
12.【答案】± -a i
13.【答案】2 3
14.【答案】 200 3 ,400
15.【答案】(1)λ=- 73
(2) 134
【分析】(1)首先求出 2a- c,b+ 2c ,依题意存在唯一的实数n,使得 2a- c=n b+2c ,即可得到方程
组,解得即可;
(2)用 e1 , e2作为基底,根据向量相等,得到方程组,解得即可;
【详解】(1)解:因为 a= 3e1+ e2,b=-2e1+ 2e2,c
= λe1- 3e2
所以 2a - c = 6-λ e1+ 5e
2,b+ 2c= 2λ-2 e1- 4e2.
因为 2a- c与 b+ 2c共线,所以存在唯一的实数n,使得 2a- c=n b+2c ,
6-λ=n 2λ-2 λ=-
7
6-λ e1+ 5e2= 2λ-2 ne - 4ne 31 2,即 =- ,解得5 4n 5 .n=- 4
(2)解:因为 a= 3e1+ e2,b=-2e1+ 2e
2,c= λe1- 3e2,且 c
= 12 a
+ μb,
3
所以 λe1- 3e2= 2 e1+
1
2 e2- 2μe1+ 2μe2=
3
2 -2μ e
1
1+ 2 +2μ e2,
λ=
3
2 -2μ, 7
所以 1 ,解得 λ= 5,μ=- ,-3= +2μ 42
所以 λ+ μ= 5- 7 134 = 4 .
16.【答案】(1)a= 0.15,6.92小时
(2) 15
【分析】(1)利用频率分布直方图各矩形面积和为 1求出 a的值,再根据频率分布直方图平均数的计算公
式求平均数即可;
(2)利用分层抽样的定义求出各组的人数,然后利用列举法求概率即可.
【详解】(1)依题意可得 0.02+0.05+0.1+a+0.18 × 2= 1,解得 a= 0.15,
又由频率分布直方图可得 3×0.02+5×0.18+7×0.15+9×0.1+11×0.05 × 2= 6.92,
所以估计全校学生周平均阅读时间的平均数为 6.92小时.
(2)由频率分布直方图可知 6,8 , 8,10 和 10,12 三组的频率的比为 0.15 : 0.1 : 0.05= 3 : 2 : 1,
所以利用分层抽样的方法抽取 6人,这三组被抽取的人数分别为 3 , 2 , 1,
记 6,8 中的 3人为 a1 , a2 , a3 , 8,10 中的 2人为 b1 , b2 , 10,12 中的 2人为 c1,
从这 6人中随机选出 2人,
则样本空间Ω= a1a2,a1a3,a1b1,a1b2,a1c1,a2a3,a2b1,a2b2,a2c1,a3b1,a3b2,a3c1,b1b2,b1c1,b2c1 共 15个样
本点,
数学试题 第 5 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
设事件A :选出的 2人都来自 6,8 ,则A= a1a2,a1a3,a2a3 共 3个样本点,
所以P A = 3 1 15 = 5 .
17.【答案】(1)证明见解析
(2) 2
【分析】(1) sinB a+c根据题意,化简得到 = ,结合正弦定理,即可得证;
sinA b
(2)由 (1) c+a和余弦定理,化简得 cosA= ,再由正弦定理,得到 sin B-A = sinA,得到B= 2A,求2b
1 a 1
得 2 < cosA< 1,得到 cosA+ = cosA+ ,结合基本不等式,即可求解.b 2cosA
sin 2A+B sin A+B +A( )
-2cos A+B sinA
【详解】 1 解:因为 - 2cos A+B = ,
sinA sinA
sin A+B cosA+cos A+B sinA-2cos A+B sinA=
sinA
sin A+B cosA-cos A+B sinA sin A+B -A= = = sinB
sinA sinA sinA
sinB = a+c b a+c可得 ,由正弦定理得 a = ,即 b
2- a2= ac.
sinA b b
2 2 2
(2) b +c -a解:由余弦定理得 cosA= ,因为 b2- a2= ac c+a,所以 cosA= ,
2bc 2b
可得 2bcosA= a+ c,所以由正弦定理可得
2sinBcosA= sinC+ sinA= sin A+B + sinA,
= sinAcosB+ cosAsinB+ sinA,
即 sinBcosA- sinAcosB= sin(B-A) = sinA,
即 sin B-A = sinA,故B= 2A,
π 1
又因为C= π-A-B= π- 3A,所以 0所以 cosA+ a = cosA+ sinAsinB = cosA+
1 ≥ 2,
b 2cosA
当且仅当 cosA= 2 = cosA+ a2 时,“ ”成立,故 的最小值为 2 .b
18.【答案】(1) (ⅰ)90°;(ⅱ) 2 ,4 2
(2) π3 .
【分析】(1) (ⅰ)先由AE CD等条件得出 sin∠CDA的值,再利用三角形全等得到CF⊥AD,接着因
为PH⊥平面ACDE,结合线面垂直性质与判定,证明CF⊥PA.
(ⅱ)解法一,先找外接球球心O在PH上,用勾股定理求半径R,再求EO,进而得EM最值与范围.
解法二,建立空间直角坐标系,写出点坐标,根据外接球性质求球心O坐标与半径R,最后求EO得出
EM范围.
(2)解法一:先作辅助线找二面角平面角∠MPN,因PA=PC,K为P在平面ACDE射影且是MN中
点,∠MPK=∠NPK.tan∠MPK= 3PK ,∠MPN最小则∠MPK最小,PK最大时∠MPK最小,K为AC
中点时PK最大,进而得二面角最小值.
解法二:取AC 中点Q建系,求各点及向量坐标.再分别求平面PAE和PCD法向量m、n.用向量夹角
公式求 cosφ,根据 sinθ取值求 cosφ最大值,从而得二面角 φ最小值.
【详解】(1) (ⅰ)如图,设CF与AD交于点G,
数学试题 第 6 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
由题可得AE CD,AD= AC2+CD2= 4,
则 sin∠CDA= sin∠DAE= 32 ,
所以∠CDA=∠DAE= π3 ,又AD=AE,所以△ADE为正三角形,
所以∠EDA=∠CDA= π3 ,又DF=
1
2 DE=CD,DG=DG,
故△DFG≌△DCG,所以FG=CG,故CF⊥AD.
因为PH⊥平面ACDE,CF 平面ACDE,所以CF⊥PH,
因为PH∩AD=H,PH ,AD 平面PAD,
所以CF⊥平面PAD,又PA 平面PAD,所以CF⊥PA,
即异面直线PA与CF所成角的大小为 90°.
(ⅱ) 1解法一:由 (ⅰ)AH= 2 AD= 2,由题可得PH= PA
2-AH 2= 2 2,
△ACD为直角三角形,且PH⊥平面ACDE,所以三棱锥P-ACD的外接球球心O在直线PH上,
设球O的半径为R,则OH= 2 2-R ,
如图,连接AO,在Rt△AOH中,OH 2+AH 2=OA2,即 2 2-R 2 + 22=R2,
3 2
得R= 2 .
2
连接EO,HE,因为OH= 2 ,HE= 2 3,
2
所以EO= OH 2+EH 2= 22 + 2 3 2= 5 2 2 ,
所以EM的最小值为EO-R= 2,EM的最大值为EO+R= 4 2,
故EM的取值范围为 2 ,4 2 .
解法二:
以H为坐标原点,点F ,H所在直线为 x轴,平面ACDE内过H且与 x轴垂直的直线为 y轴,HP所在
直线为 z轴,建立如图所示的空间直角坐标系,
数学试题 第 7 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
则A 1,- 3 ,0 ,C 1, 3 ,0 ,D -1, 3 ,0 ,P 0,0,2 2 ,E -3,- 3 ,0 .
设球心O x,y,z ,连接OA,OC,OD,OP,因为OA=OC=OD=OP,
所以 x-1 2 + y+ 3 2 +z2= x-1 2 + y- 3 2 +z2
= x+1 2 + y- 3 2 +z2= x2+y2+ z-2 2 2 ,
x= y= 0 z= 2 O 0,0, 2 O R= 2 2- 2 = 3 2解得 , 2 ,故 2 ,所以球 的半径 2 2 .
2 2(另解:可以通过R=OA得到R= 0-1 2 + 0+ 3 2+ = 3 2 2 2 )
2 5 2
连接EO,因为E -3,- 3 ,0 ,所以EO= 32+ 3 2 + 22 = 2 ,
所以EM的最小值为EO-R= 2,EM的最大值为EO+R= 4 2,
故EM的取值范围为 2 ,4 2 .
(2)解法一 如图,过点P作平行于AE的直线,则该直线为平面PCD与平面PAE的交线 l.
设点P在平面ACDE内的射影为K,过点K作平行于AC的直线分别交CD,AE于点M ,N,连接PM
,PN,则∠MPN为二面角A- l-C的平面角.
因为PA=PC,所以KA=KC,K为MN的中点,PM=PN,
连接PK,则∠MPK=∠NPK,
tan∠MPK= MK 3PK = PK .
若∠MPN最小,则∠MPK最小,即 tan∠MPK最小,
所以当PK取最大值时,二面角A- l-C取得最小值.
易知当点K为AC的中点时,PK取得最大值,且最大值为 3,
因此 tan∠MPK 3 π的最小值为 3 ,即∠MPK的最小值为 6 ,
所以二面角A- l-C π的最小值为 3 .
解法二:取AC的中点Q,连接PQ,QF,则PQ⊥AC,PQ= 3,QF= 3,
以Q为坐标原点,分别以FQ,QC所在直线为 x , y轴,过点Q与平面ACDE垂直的直线为 z轴,建立
数学试题 第 8 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
如图所示的空间直角坐标系,
则A 0,- 3 ,0 ,C 0, 3 ,0 ,D -2, 3 ,0 ,E -4,- 3 ,0 ,
所以DC = 2,0,0 ,EA= 4,0,0 .设∠PQx= θ 0≤θ≤π ,则P 3cosθ,0,3sinθ ,
所以AP= 3cosθ, 3 ,3sinθ ,CP= 3cosθ,- 3 ,3sinθ .
设平面PAE 的法向量为m= x1,y1,z1 ,
m
A P =0 3cosθ x1+ 3y1+3sinθ z =0则 ,即
1 ,
m EA=0 4x1=0
取 z1=-1,则 x1= 0,y1= 3sinθ
,故m= 0, 3sinθ,-1 为平面PAE的一个法向量.
设平面PCD 的法向量为n= a,b,c ,
n
C P =0 3cosθ a- 3b+3sinθ c=0则 ,即n DC=0 2a= ,0
c= 1 a= 0 b= 3sinθ n 取 ,则 , ,故 = 0, 3sinθ,1 为平面PCD的一个法向量.
易知此时m与n的夹角即二面角A- l-C的平面角.(取 c=-1,则n= 0,- 3sinθ,-1 ,此时m 与n
的夹角为二面角A- l-C的平面角的补角)
设二面角A- l-C的大小为 φ,
m n 2
则 cosφ= cosm ,n = 3sin θ-1 2 1
=
3sin2
= 1- 2 ≤ 2 ,m n θ+1 3sin θ+1
所以当 sinθ= 1时,cosφ 1 π π取得最大值 2 ,此时 φ取得最小值 3 ,故二面角A- l-C的最小值为 3 .
19.【详解】(1)因为 f(1)≤ 2,所以 1-a - 1+ a≤ 2,解得 a≤ 2.
x-
1
x ,x≥a,(2)因为 f(x) =
-x- 1 x +2a,x当 a≤ 0时,f(x) = x- 1x 在 0,+∞ 上递增,
0< a≤ 1 f(x) =-x- 1当 时, x + 2a在 (0 , a]
1
上递增,f(x) = x- x 在 [a ,+∞)上递增.
因此,当 a≤ 1时不存在两个不相等的正实数 x1 , x2满足 f x1 = f x2 .
当 a> 1时,f(x)在 (0 , 1]上递增,在 1,a 上递减,在 [a ,+∞)上递增,
所以,存在两个不相等的正实数 x1 , x2,满足 f x1 = f x2 .因此 a> 1.
(i)当 1< a< 2时,f(x) 1的最小值为 a- a ;
当 a≥ 2时,f(x)的最小值为 2a- 52 .
(ii)不妨设 x1< x2,
数学试题 第 9 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
当 0< x1< x2≤ a时,f x 11 = f x2 即-x1- x + 2a=-x -
1
2 x + 2a,1 2
得 x1 x2= 1,所以,x1+ x2> 2 , x1+ x2< 2a;
当 0< x1< a< x 1 12时,f x1 = f x2 即-x1- x + 2a= x2- x ,1 2
1 1
所以,x1+ x2= x - x + 2a< 2a,2 1
又因为 x2> a,即 x2> 2a- x2,所以-x - 11 x + 2a> 2a- x2-
1
x ,得 x1 x2> 1.1 2
所以 2< x1+ x2< 2a.
数学试题 第 10 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
★祝大家学习生活愉快★
注意事项:
1.答卷前,考生务必用黑色字迹的钢笔或签字笔将自己的姓名和考生号,试室号,座位号填写在答题
卡上。用 2B铅笔将试卷类型和考生号填涂在答题卡相应位置上。
2.选择题每小题选出答案后,用 2B铅笔把答题卡上对应的题目选项的答案信息点涂黑;如需改动,用
橡皮擦干净后,再填涂其他答案。答案不能答在试卷上。
3.非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卡各题目指定区域内相应位置
上;如需改动,先划掉原来的答案,然后再写上新的答案,不准使用铅笔和涂改液。不按以上要求作答的答
案无效。
一、单选题:本题共 8小题,每小题 5分,共 40分,每小题只有一个选项符合要求
1.设集合A= 3,4,5 ,B= 2,3,4,8 ,则图中阴影部分表示的集合为 ( )
A. 2,8 B. 3,4
C. 2,5,8 D. 3,4,5
2. “ac= bc”是“a= b”的 ( )
A. 充分不必要条件 B. 必要不充分条件 C. 充要条件 D. 既不充分也不必要条件
3.在某次全市高三模拟考试后,数学老师随机抽取了 6名同学的第一个解答题的得分情况如下:7,10,5,
8,4,2,则这组数据的平均数和 30%分位数分别为 ( )
A. 6,3 B. 5,3 C. 5,4 D. 6,4
4.在三棱锥P-ABC中,PA=BC= 10,PB=AC= 5,PC=AB= 13,则该三棱锥的外接球的表
面积为 ( )
A. 28π B. 28 73 π C. 7π D. 14π
5.在平面直角坐标系 xOy中,角 α与角 β均以 x轴的非负半轴为始边,它们的终边关于直线 y=-x对称.
3
若角 α的终边与单位圆交点P的纵坐标为 5 ,则 cosβ= ( )
A. 3 B. - 3 C. 45 5 5 D. -
4
5
6.Deepseek(深度求索)是人工智能的一种具有代表性的实现方法,它是以神经网络为出发点.在神经网络
G
优化中,指数衰减的学习率模型为 L=L DG00 ,其中L表示每一轮优化时使用的学习率,L0表示初始学习
率,D表示衰减系数,G表示训练迭代轮数,G0表示衰减速度.已知某个指数衰减的学习率模型的初始
学习率 L0为 0.6,衰减速度G0为 20,且当训练迭代轮数为 10时,学习率衰减为 0.3,则学习率衰减到 0.2
以下 (不含 0.2)所需的训练迭代轮数至少为 ( )
(参考数据:lg2≈ 0.3,lg3≈ 0.477)
A. 14 B. 15 C. 16 D. 17
数学试题 第 1 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
2 2
7.已知函数 f x 1 = 2x+ x-1 的对称中心在直线 y= ax+ b a>0
a +2b
上,则 2a 的最小值为 ( )
A. 4 3- 4 B. 4 3+ 4 C. 2 6- 4 D. 2 6+ 4
8. 已知平面向量 a,b,c满足:a与 b的夹角为锐角, a = 2, b = 4, c = 1,且 t∈R, b+ta ≥ b-a ,
则 c -a c - 12 b 的最小值是 ( )
A. 0 B. 3+ 2 3 C. 6 D. 3- 2 3
二、多选题:本题共 3小题,每小题 6分,共 18分。在每小题给出的四个选项中,有多项符合题目要求。全
部选对的得 6分,部分选对的得部分分,有选错的得 0分。
9.已知事件A ,B,且P A = 0.4 ,P B = 0.5,则 ( )
A. 事件A与事件B互为对立事件 B. 若事件A与事件B互斥,则P A∪B = 0.9
C. 若事件A与事件B互斥,则P AB = 0.2 D. 若P AB = 0.3,则事件A与事件B相互独立
10.如图是一个棱长为 1的正方体的展开图,其中M,N分别为CH,DB的中点.如果将它还原成正方体,
那么下列选项中正确的是 ( )
A. π直线AB与CD所成角为 3
B. 直线EF与GH平行
C. 经过DEMN 9四个点的球的表面积为 4 π
D. P 7是正方形GKHI内的动点,若 |AP| = 2 ,那么 P点的轨迹长为
3
4 π
11.已知函数 f x = sinx+cos x sinx-cosx ,下列说法正确的是 ( )
A. f(x)的周期为 2π
B. f(x) π π在区间 - , 2 2 上是增函数
C. 若 f x1 + f x = 2 x + x = kπ 2 ,则 1 2 2 (k∈ Z)
D. 函数 g(x) = f(x) + 1在区间 [0 , 2π]上有且仅有 2个零点
三、填空题:本题共 3小题,每小题 5分,共 15分
12.在复数范围内,a a<0 的所有平方根为 .
13.某海警船在A处看灯塔B在它的北偏东 75°,距离为 3 6nmile,在A处看灯塔C
在海警船的北偏西 30°,距离为 2 3nmile,海警船由A处向正北航行到D处时,
再看灯塔B在南偏东 60°,则灯塔C与D处之间的距离为 nmile.
14.在三棱锥A-BCD中,AC⊥AB ,BD⊥AB,且AC=BD= 20 ,AB= 6,若三
棱锥A-BCD的外接球表面积的取值范围为 661π,1636π ,则三棱锥A-BCD
体积的取值范围为 .
数学试题 第 2 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
四、解答题:本题共 5小题,共 77分,解答应写出文字说明,证明过程或演算步骤
15. (13 ) e e a= 3e + e b=-2e + 2e c
分 已知 1, 2是平面内一对不共线的向量,且 1 2, 1 2, = λe1- 3e2.
(1) 2a - c
若 与 b+ 2c 共线,求实数 λ的值;
(2) c 若 = 12 a
+ μb,求 λ+ μ的值.
16. (15分)某校开展一项名为“书香致远,阅读润心”的读书活动,为了更好地服务全校学生,需要对全校学
生的周平均阅读时间进行调查,现从该校学生中随机抽取 200名学生,将他们的周平均阅读时间 (单位:
小时)数据分成 5组: 2,4 , 4,6 , 6,8 , 8,10 , 10,12 ,根据分组数据制成了如图所示的频率分布
直方图.
(1)求 a的值,并估计全校学生周平均阅读时间的平均数;
(2)用分层抽样的方法从周平均阅读时间不小于 6小时的学生中抽出 6人,从这 6人中随机选出 2人作为
该活动的形象大使,求这 2人都来自 6,8 这组的概率.
sin 2A+B
17. ( 15分)已知 a , b , c a+c分别为△ABC三个内角A ,B ,C的对边,且 - 2cos A+B = .
sinA b
(1)证明:b2- a2= ac;
(2) cosA+ a求 的最小值.
b
数学试题 第 3 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
18. (17分)如图 1,在平面五边形ABCDE中,∠EAC=∠DCA= π2 ,AE= 4,CD= 2,AB= BC=AC=
2 3,F ,H分别为ED ,AD的中点,将△ABC沿AC翻折,使点B到点P的位置,如图 2.
(1)若PH⊥平面ACDE.
(ⅰ)求异面直线PA与CF所成角的大小;
(ⅱ)三棱锥P-ACD的各顶点都在球O上,M为球O球面上的动点,求EM的取值范围.
(2)在翻折的过程中,设平面PCD与平面PAE的交线为 l,求二面角A- l-C的最小值.
19. (17分)已知函数 f x = x-a - 1 x + a , a∈R.
(1)若 f 1 ≤ 2,求 a的取值范围;
(2)若存在两个不相等的正实数 x1 , x2,满足 f x1 = f x2 .
(i)求 y= f x 在 x∈ 1,2 上的最小值;
(ii)证明:2< x1+ x2< 2a.
数学试题 第 4 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
参考答案
CBDDBCCD
BD ACD ACD
12.【答案】± -a i
13.【答案】2 3
14.【答案】 200 3 ,400
15.【答案】(1)λ=- 73
(2) 134
【分析】(1)首先求出 2a- c,b+ 2c ,依题意存在唯一的实数n,使得 2a- c=n b+2c ,即可得到方程
组,解得即可;
(2)用 e1 , e2作为基底,根据向量相等,得到方程组,解得即可;
【详解】(1)解:因为 a= 3e1+ e2,b=-2e1+ 2e2,c
= λe1- 3e2
所以 2a - c = 6-λ e1+ 5e
2,b+ 2c= 2λ-2 e1- 4e2.
因为 2a- c与 b+ 2c共线,所以存在唯一的实数n,使得 2a- c=n b+2c ,
6-λ=n 2λ-2 λ=-
7
6-λ e1+ 5e2= 2λ-2 ne - 4ne 31 2,即 =- ,解得5 4n 5 .n=- 4
(2)解:因为 a= 3e1+ e2,b=-2e1+ 2e
2,c= λe1- 3e2,且 c
= 12 a
+ μb,
3
所以 λe1- 3e2= 2 e1+
1
2 e2- 2μe1+ 2μe2=
3
2 -2μ e
1
1+ 2 +2μ e2,
λ=
3
2 -2μ, 7
所以 1 ,解得 λ= 5,μ=- ,-3= +2μ 42
所以 λ+ μ= 5- 7 134 = 4 .
16.【答案】(1)a= 0.15,6.92小时
(2) 15
【分析】(1)利用频率分布直方图各矩形面积和为 1求出 a的值,再根据频率分布直方图平均数的计算公
式求平均数即可;
(2)利用分层抽样的定义求出各组的人数,然后利用列举法求概率即可.
【详解】(1)依题意可得 0.02+0.05+0.1+a+0.18 × 2= 1,解得 a= 0.15,
又由频率分布直方图可得 3×0.02+5×0.18+7×0.15+9×0.1+11×0.05 × 2= 6.92,
所以估计全校学生周平均阅读时间的平均数为 6.92小时.
(2)由频率分布直方图可知 6,8 , 8,10 和 10,12 三组的频率的比为 0.15 : 0.1 : 0.05= 3 : 2 : 1,
所以利用分层抽样的方法抽取 6人,这三组被抽取的人数分别为 3 , 2 , 1,
记 6,8 中的 3人为 a1 , a2 , a3 , 8,10 中的 2人为 b1 , b2 , 10,12 中的 2人为 c1,
从这 6人中随机选出 2人,
则样本空间Ω= a1a2,a1a3,a1b1,a1b2,a1c1,a2a3,a2b1,a2b2,a2c1,a3b1,a3b2,a3c1,b1b2,b1c1,b2c1 共 15个样
本点,
数学试题 第 5 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
设事件A :选出的 2人都来自 6,8 ,则A= a1a2,a1a3,a2a3 共 3个样本点,
所以P A = 3 1 15 = 5 .
17.【答案】(1)证明见解析
(2) 2
【分析】(1) sinB a+c根据题意,化简得到 = ,结合正弦定理,即可得证;
sinA b
(2)由 (1) c+a和余弦定理,化简得 cosA= ,再由正弦定理,得到 sin B-A = sinA,得到B= 2A,求2b
1 a 1
得 2 < cosA< 1,得到 cosA+ = cosA+ ,结合基本不等式,即可求解.b 2cosA
sin 2A+B sin A+B +A( )
-2cos A+B sinA
【详解】 1 解:因为 - 2cos A+B = ,
sinA sinA
sin A+B cosA+cos A+B sinA-2cos A+B sinA=
sinA
sin A+B cosA-cos A+B sinA sin A+B -A= = = sinB
sinA sinA sinA
sinB = a+c b a+c可得 ,由正弦定理得 a = ,即 b
2- a2= ac.
sinA b b
2 2 2
(2) b +c -a解:由余弦定理得 cosA= ,因为 b2- a2= ac c+a,所以 cosA= ,
2bc 2b
可得 2bcosA= a+ c,所以由正弦定理可得
2sinBcosA= sinC+ sinA= sin A+B + sinA,
= sinAcosB+ cosAsinB+ sinA,
即 sinBcosA- sinAcosB= sin(B-A) = sinA,
即 sin B-A = sinA,故B= 2A,
π 1
又因为C= π-A-B= π- 3A,所以 0
1 ≥ 2,
b 2cosA
当且仅当 cosA= 2 = cosA+ a2 时,“ ”成立,故 的最小值为 2 .b
18.【答案】(1) (ⅰ)90°;(ⅱ) 2 ,4 2
(2) π3 .
【分析】(1) (ⅰ)先由AE CD等条件得出 sin∠CDA的值,再利用三角形全等得到CF⊥AD,接着因
为PH⊥平面ACDE,结合线面垂直性质与判定,证明CF⊥PA.
(ⅱ)解法一,先找外接球球心O在PH上,用勾股定理求半径R,再求EO,进而得EM最值与范围.
解法二,建立空间直角坐标系,写出点坐标,根据外接球性质求球心O坐标与半径R,最后求EO得出
EM范围.
(2)解法一:先作辅助线找二面角平面角∠MPN,因PA=PC,K为P在平面ACDE射影且是MN中
点,∠MPK=∠NPK.tan∠MPK= 3PK ,∠MPN最小则∠MPK最小,PK最大时∠MPK最小,K为AC
中点时PK最大,进而得二面角最小值.
解法二:取AC 中点Q建系,求各点及向量坐标.再分别求平面PAE和PCD法向量m、n.用向量夹角
公式求 cosφ,根据 sinθ取值求 cosφ最大值,从而得二面角 φ最小值.
【详解】(1) (ⅰ)如图,设CF与AD交于点G,
数学试题 第 6 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
由题可得AE CD,AD= AC2+CD2= 4,
则 sin∠CDA= sin∠DAE= 32 ,
所以∠CDA=∠DAE= π3 ,又AD=AE,所以△ADE为正三角形,
所以∠EDA=∠CDA= π3 ,又DF=
1
2 DE=CD,DG=DG,
故△DFG≌△DCG,所以FG=CG,故CF⊥AD.
因为PH⊥平面ACDE,CF 平面ACDE,所以CF⊥PH,
因为PH∩AD=H,PH ,AD 平面PAD,
所以CF⊥平面PAD,又PA 平面PAD,所以CF⊥PA,
即异面直线PA与CF所成角的大小为 90°.
(ⅱ) 1解法一:由 (ⅰ)AH= 2 AD= 2,由题可得PH= PA
2-AH 2= 2 2,
△ACD为直角三角形,且PH⊥平面ACDE,所以三棱锥P-ACD的外接球球心O在直线PH上,
设球O的半径为R,则OH= 2 2-R ,
如图,连接AO,在Rt△AOH中,OH 2+AH 2=OA2,即 2 2-R 2 + 22=R2,
3 2
得R= 2 .
2
连接EO,HE,因为OH= 2 ,HE= 2 3,
2
所以EO= OH 2+EH 2= 22 + 2 3 2= 5 2 2 ,
所以EM的最小值为EO-R= 2,EM的最大值为EO+R= 4 2,
故EM的取值范围为 2 ,4 2 .
解法二:
以H为坐标原点,点F ,H所在直线为 x轴,平面ACDE内过H且与 x轴垂直的直线为 y轴,HP所在
直线为 z轴,建立如图所示的空间直角坐标系,
数学试题 第 7 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
则A 1,- 3 ,0 ,C 1, 3 ,0 ,D -1, 3 ,0 ,P 0,0,2 2 ,E -3,- 3 ,0 .
设球心O x,y,z ,连接OA,OC,OD,OP,因为OA=OC=OD=OP,
所以 x-1 2 + y+ 3 2 +z2= x-1 2 + y- 3 2 +z2
= x+1 2 + y- 3 2 +z2= x2+y2+ z-2 2 2 ,
x= y= 0 z= 2 O 0,0, 2 O R= 2 2- 2 = 3 2解得 , 2 ,故 2 ,所以球 的半径 2 2 .
2 2(另解:可以通过R=OA得到R= 0-1 2 + 0+ 3 2+ = 3 2 2 2 )
2 5 2
连接EO,因为E -3,- 3 ,0 ,所以EO= 32+ 3 2 + 22 = 2 ,
所以EM的最小值为EO-R= 2,EM的最大值为EO+R= 4 2,
故EM的取值范围为 2 ,4 2 .
(2)解法一 如图,过点P作平行于AE的直线,则该直线为平面PCD与平面PAE的交线 l.
设点P在平面ACDE内的射影为K,过点K作平行于AC的直线分别交CD,AE于点M ,N,连接PM
,PN,则∠MPN为二面角A- l-C的平面角.
因为PA=PC,所以KA=KC,K为MN的中点,PM=PN,
连接PK,则∠MPK=∠NPK,
tan∠MPK= MK 3PK = PK .
若∠MPN最小,则∠MPK最小,即 tan∠MPK最小,
所以当PK取最大值时,二面角A- l-C取得最小值.
易知当点K为AC的中点时,PK取得最大值,且最大值为 3,
因此 tan∠MPK 3 π的最小值为 3 ,即∠MPK的最小值为 6 ,
所以二面角A- l-C π的最小值为 3 .
解法二:取AC的中点Q,连接PQ,QF,则PQ⊥AC,PQ= 3,QF= 3,
以Q为坐标原点,分别以FQ,QC所在直线为 x , y轴,过点Q与平面ACDE垂直的直线为 z轴,建立
数学试题 第 8 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
如图所示的空间直角坐标系,
则A 0,- 3 ,0 ,C 0, 3 ,0 ,D -2, 3 ,0 ,E -4,- 3 ,0 ,
所以DC = 2,0,0 ,EA= 4,0,0 .设∠PQx= θ 0≤θ≤π ,则P 3cosθ,0,3sinθ ,
所以AP= 3cosθ, 3 ,3sinθ ,CP= 3cosθ,- 3 ,3sinθ .
设平面PAE 的法向量为m= x1,y1,z1 ,
m
A P =0 3cosθ x1+ 3y1+3sinθ z =0则 ,即
1 ,
m EA=0 4x1=0
取 z1=-1,则 x1= 0,y1= 3sinθ
,故m= 0, 3sinθ,-1 为平面PAE的一个法向量.
设平面PCD 的法向量为n= a,b,c ,
n
C P =0 3cosθ a- 3b+3sinθ c=0则 ,即n DC=0 2a= ,0
c= 1 a= 0 b= 3sinθ n 取 ,则 , ,故 = 0, 3sinθ,1 为平面PCD的一个法向量.
易知此时m与n的夹角即二面角A- l-C的平面角.(取 c=-1,则n= 0,- 3sinθ,-1 ,此时m 与n
的夹角为二面角A- l-C的平面角的补角)
设二面角A- l-C的大小为 φ,
m n 2
则 cosφ= cosm ,n = 3sin θ-1 2 1
=
3sin2
= 1- 2 ≤ 2 ,m n θ+1 3sin θ+1
所以当 sinθ= 1时,cosφ 1 π π取得最大值 2 ,此时 φ取得最小值 3 ,故二面角A- l-C的最小值为 3 .
19.【详解】(1)因为 f(1)≤ 2,所以 1-a - 1+ a≤ 2,解得 a≤ 2.
x-
1
x ,x≥a,(2)因为 f(x) =
-x- 1 x +2a,x
0< a≤ 1 f(x) =-x- 1当 时, x + 2a在 (0 , a]
1
上递增,f(x) = x- x 在 [a ,+∞)上递增.
因此,当 a≤ 1时不存在两个不相等的正实数 x1 , x2满足 f x1 = f x2 .
当 a> 1时,f(x)在 (0 , 1]上递增,在 1,a 上递减,在 [a ,+∞)上递增,
所以,存在两个不相等的正实数 x1 , x2,满足 f x1 = f x2 .因此 a> 1.
(i)当 1< a< 2时,f(x) 1的最小值为 a- a ;
当 a≥ 2时,f(x)的最小值为 2a- 52 .
(ii)不妨设 x1< x2,
数学试题 第 9 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
当 0< x1< x2≤ a时,f x 11 = f x2 即-x1- x + 2a=-x -
1
2 x + 2a,1 2
得 x1 x2= 1,所以,x1+ x2> 2 , x1+ x2< 2a;
当 0< x1< a< x 1 12时,f x1 = f x2 即-x1- x + 2a= x2- x ,1 2
1 1
所以,x1+ x2= x - x + 2a< 2a,2 1
又因为 x2> a,即 x2> 2a- x2,所以-x - 11 x + 2a> 2a- x2-
1
x ,得 x1 x2> 1.1 2
所以 2< x1+ x2< 2a.
数学试题 第 10 页 共 10 页
{#{QQABCQA84gA4kATACI4LEUE8CAmQkIAgJeokgQCWuA4jyRFABAA=}#}
同课章节目录
