12.2.1 扇形图、条形图和折线图 课件(共41张PPT)
文档属性
| 名称 | 12.2.1 扇形图、条形图和折线图 课件(共41张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 00:00:00 | ||
图片预览








文档简介
(共41张PPT)
第十二章 数据的收集、整理与描述
12.2 用统计图描述数据
12.2.1 扇形图、条形图和折线图
目
录
1. 学习目标
4. 知识点1 扇形统计图
7. 课堂小结
8. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 条形图和折线图
10. 拓展与延伸
9. 对接中考
3. 新课导入
6. 知识点3 条形图和折线图
1. 会绘制扇形图,能读懂扇形图、条形图、折线图反映的数据信息.
2. 能清晰认识不同统计图之间的差异与联系;在实际应用中能准确选择合适的统计图,培养数据分析能力.
3. 能用扇形图、条形图、折线图整理与描述收集到的数据,能根据统计图表分析随机现象的变化趋势,体会数据分析的必要性,形成数据观念.
学习目标
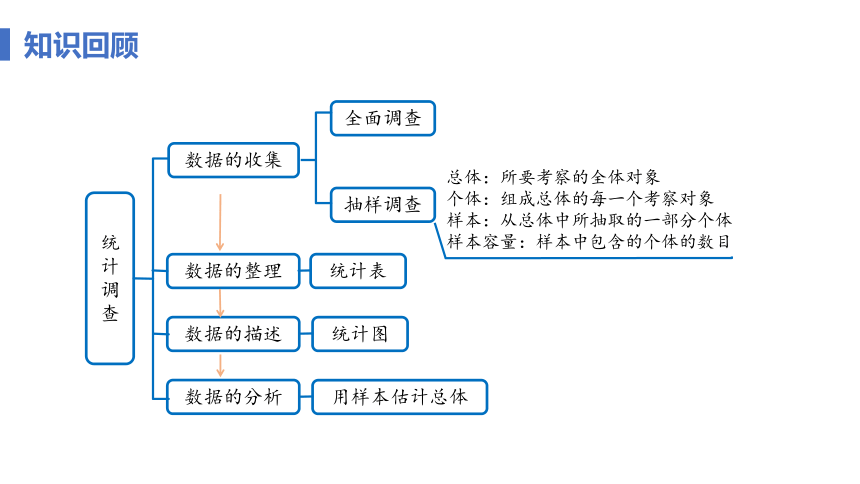
知识回顾
数据的收集
数据的整理
统计调查
全面调查
抽样调查
总体:所要考察的全体对象
个体:组成总体的每一个考察对象
样本:从总体中所抽取的一部分个体
样本容量:样本中包含的个体的数目
数据的描述
数据的分析
统计表
统计图
用样本估计总体
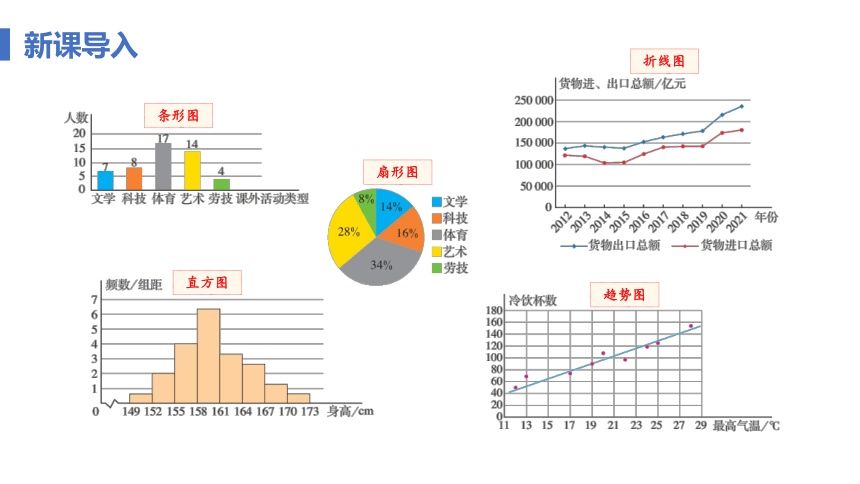
新课导入
条形图
扇形图
折线图
直方图
趋势图
新课讲解
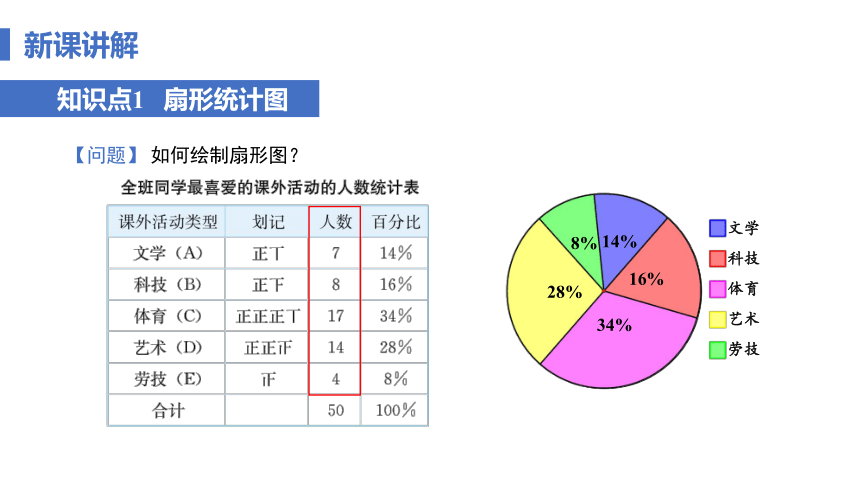
知识点1 扇形统计图
【问题】 如何绘制扇形图?
文学
科技
体育
艺术
劳技
14%
16%
34%
28%
8%
新课讲解
绘制扇形图的步骤:
1. 算:根据各部分占总体的百分比.
2. 求:求各部分对应扇形的圆心角的度数,即360°×各部分占总体的百分比.
3. 画:取适当的半径画圆,利用量角器作出各圆心角,在圆内画出各个扇形.
4. 标:在相应的扇形上注明各类别的名称及其相应的百分比.
扇形图用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
新课讲解
1. 某学校对全校500名学生进行了一项关于课外阅读偏好的调查,结果如下:喜欢读文学类书籍的学生有150名,喜欢读科普类书籍的学生有100名,喜欢读历史类书籍的学生有80名,喜欢读漫画类书籍的学生有60名,其余的学生则没有特定的阅读偏好.
(1)请根据以上数据,绘制一个扇形图;
解:(1)喜欢读文学类书籍的学生所占百分比=×100%=30%;
喜欢读科普类书籍的学生所占百分比=×100%=20%;
喜欢读历史类书籍的学生所占百分比= ×100%=16%;
喜欢读漫画类书籍的学生所占百分比=×100%=12%;
没有特定阅读偏好的学生所占百分比=100%-(30%+20%+ 16%+12%)=22%.
例
喜欢读文学类、科普类、历史类、漫画类及没有特定阅读偏好类所在扇形的圆心角度数依次为360°×30%=108°,360°×20%=72°, 360°×16%=57.6°,360°×12%=43.2°,360°×22%=79.2°.
画扇形图如图所示.
新课讲解
1. 某学校对全校500名学生进行了一项关于课外阅读偏好的调查,结果如下:喜欢读文学类书籍的学生有150名,喜欢读科普类书籍的学生有100名,喜欢读历史类书籍的学生有80名,喜欢读漫画类书籍的学生有60名,其余的学生则没有特定的阅读偏好.
(2)没有特定阅读偏好的学生有多少名?
例
画扇形图如图所示.
解:(2)因为没有特定阅读偏好的学生所占的百分比是22%,
所以没有特定阅读偏好的学生有500×22%=110(名).
新课讲解
练一练
1. 一所中学准备搬迁到新校舍,在迁校舍前对该校 300名学生如何到新校舍进行了一次调查,调查结果如下表.
请你根据表中数据画出表示调查结果的扇形统计图.
步行 骑自行车 乘公交车 其他
60 人 105 人 120 人 15 人
解:各部分占总体的百分比分别为:
步行:60÷300=20%,
骑自行车:105÷300=35%,
乘公交车:120÷300=40%,
其他:15÷300 = 5%.
所 对 应 扇 形 圆 心 角 的 度 数 分 别 为
360°× 20%=72° ,360°× 35%=126° ,
360°× 40%=144° ,360°× 5%=18° .
扇形统计图如图 所示 .
新课讲解
练一练
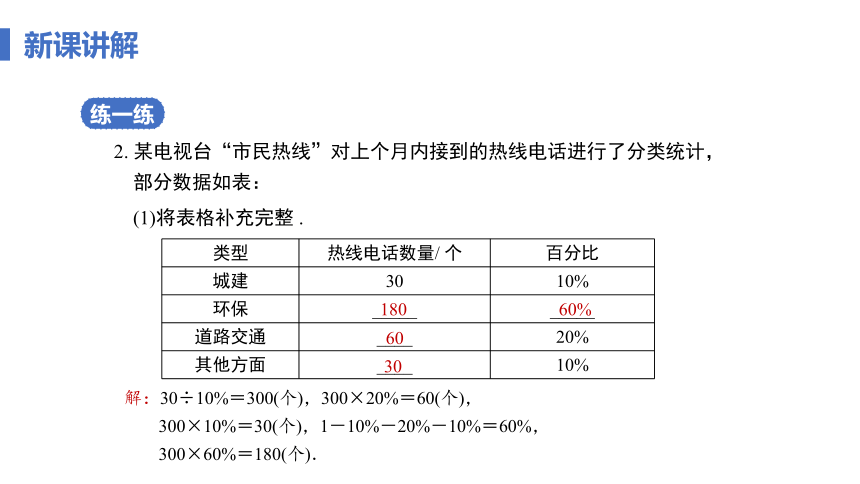
2. 某电视台“市民热线”对上个月内接到的热线电话进行了分类统计,部分数据如表:
(1)将表格补充完整 .
类型 热线电话数量/ 个 百分比
城建 30 10%
环保 _____ _____
道路交通 ____ 20%
其他方面 ____ 10%
解:30÷10%=300(个),300×20%=60(个),
300×10%=30(个),1-10%-20%-10%=60%,
300×60%=180(个).
180
60%
60
30
新课讲解
练一练
2. 某电视台“市民热线”对上个月内接到的热线电话进行了分类统计,部分数据如表:
(2)在扇形统计图中,各类数据对应的圆心角分别是多少度?.
(3)画出扇形统计图,标上各类型相应的百分比,并写上统计图的名称.
解:(2)在扇形统计图中,“城建”对应的圆心角度数为360×10%=36,
“环保”对应的圆心角度数为360×60%=216,
“道路交通”对应的圆心角度数为360×20%=72,
“其他方面”对应的圆心角度数为360×10%=36.
(3)画出扇形统计图如图.
电视台“市民热线”上个月内接到的热线电话类型扇形统计图
新课讲解
知识点2 条形图和折线图
条形图 扇形图 折线图
图示
新课讲解
条形图 扇形图 折线图
特点 用一个单位长度表示一定的数量 , 用宽度相同的直条的高低表示数量的多少 用整个圆表示总体,用圆内的每个扇形表示总体中的一部分,通过扇形的大小反映各个部分占总体的百分比 用一个单位长度表示一定的数量 , 用折线的起伏表示数量的增减变化
优点 能清楚地表示各部分的具体数量,便于相互比较 能清楚地表示各部分在总体中所占的百分比 能清楚地看出数量增减变化的情况 , 也能看出各部分数量的多少
缺点 不能反映各部分占总体的百分比 不能反映各部分数量的多少 不能反映各部分占总体的百分比
选用情境 比较数据之间的大小关系 表示各部分占总体的百分比 表示数据的变化趋势
1. 在同一条形图中,小长方形的宽必须相同;
2. 利用折线图比较两个统计量的变化趋势时,纵轴上同一单位长度所表示的意义必须要一致 .
注意
新课讲解
例
2. 体重指数(BMI)是衡量人体胖瘦程度的常用指标( ).某公司为了解员工的胖瘦状况,随机抽取了60名员工的体检数据,计算得到他们的体重指数数据 (单位:kg/m2),如表所示. 请选择合适的统计图,表示这个公司60名员工中各类别体重指数的员工人数和所占的百分比.同时说一说从绘制的统计图中,能获得哪些信息.
分析:可以先借助表格,统计各类别体重指数的员工人数和所占的百分比.
为了清楚地表示各类别中的人数,可以绘制条形图;为了直观地表示各类别中的人数所占的百分比,可以绘制扇形图.
新课讲解
解:根据上表中的数据,统计出这个公司60名员工的体重指数情况, 如下表所示.
分别画出条形图和扇形图,表示这个公司各类别体重指数的员工人数和所占的百分比.
新课讲解
从条形图和扇形图中可以看出,这个公司60名员工中体重正常的人数最多,有38人,所占百分比为63.3%;体重过低的人数次之,有10人,所占百分比为16.7%;超重的有7人,所占百分比为11.7%;肥胖的人数最少,有5人,所占百分比为8.3%.
由此可以推断这个公司员工的胖瘦状况.
例如,这个公司大多数员工的体重正常,但仍有大约8%的员工肥胖,需要引起注意.
新课讲解
3. 某平台发布《2024 春节档电影数据洞察报告》数据显示,春节档电影总票房创历史新高.春节档 8 天日票房收入及票房冠军电影 A 在日票房收入中所占比重分别如左图和右图所示.
例
【数据分析】
(1)下列结论中,所有正确的序号是 ________.
①初一至初八日票房收入超过 10 亿的天数占 50%;
②初一至初八电影 A 票房在日票房收入中所占比重呈先上升再下降的趋势;
③电影 A 日票房收入最高的一天是初四.
①②
新课讲解
3. 某平台发布《2024 春节档电影数据洞察报告》数据显示,春节档电影总票房创历史新高.春节档 8 天日票房收入及票房冠军电影 A 在日票房收入中所占比重分别如左图和右图所示.
例
(2)2024 春节档 8 天微博电影相关热搜总数为 946 个,将微博映后热搜类型分布、各级城市票房收入占比和观众性别占比绘制成如图 ①②③.
①求“全民讨论”的热搜个数(精确到个位).
②结合各级城市票房收入占比和观众性别占比分析,如果你是投资方,来年的春节档你投资影片会考虑哪些因素?
解:①“全民讨论”的热搜个数约为 946×57.3% ≈ 542(个) .
②由题意知四线城市占比最多,女性观众占比高于男性观众,∴ 来年的春节档投资影片会考虑女性观众的视角,投资反应社会上女性在生活、工作时真实现状的影片,在四线城市加大投放量.(合理即可)
新课讲解
练一练
1. 某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”“比较了解”“一般了解”“不了解”四种类型,分别记 为 A, B, C, D,根据调查结果绘制了如下尚不完整的扇形统计图 .
(1)本次问卷共随机调查了___ 名学生,在扇形统计图中, m=___.
(2)请根据数据信息,补全条形统计图 .
50
32
解:A类型的人数为50×16%=8,补全条形统计图如图.
(3)若该校有 1000名学生,估计选择“非常了解”“比较了解” 的学生共有多少名?
解:1 000×(16%+40%)=560(名),
答:估计选择“非常了解”“比较了解”的学生共有560名.
新课讲解
练一练
2. 七年级的所有学生都参加了社团活动,因条件限制,每名学生都只能加入一个社团. 李明对全年级同学参加社团活动的情况进行了一次调查.如图是根据李明的调查数据绘制的不完整的统计图,请根据图中信息,回答下列问题,并将统计图补充完整.
(1) 七年级共有多少名学生?
解:∵80÷40%=200(名),
∴七年级共有200名学生.
(2) 七年级有多少名学生参加篮球社?
解:∵200×10%=20(名),
∴七年级有20名学生参加篮球社.
新课讲解
练一练
2. 七年级的所有学生都参加了社团活动,因条件限制,每名学生都只能加入一个社团. 李明对全年级同学参加社团活动的情况进行了一次调查.如图是根据李明的调查数据绘制的不完整的统计图,请根据图中信息,回答下列问题,并将统计图补充完整.
(3) 七年级参加美术社的学生人数占全年级总人数的百分比是多少?
解:∵×100%=30%, ∴七年级参加美术社的学生人数占全年级总人数的30%.
(4) 将统计图补充完整.
解:统计图补充如图所示:
20
新课讲解
知识点3 复合折线图、复合条形图
4. 下表是2013—2022年我国货物出口总额与进口总额的数据.请选择合适的统计图,描述这十年我国货物进、出口总额的变化情况,并对它们进行比较.
例
分析:折线图用折线的上升或下降表示数据的增减变化情况,有利于描述数据的发展趋势;条形图能直观地表示各个数据的大小,便于比较数据.因此,可以绘制折线图或条形图描述这十年我国货物进、出口总额各自的变化情况.而要比较货物出口总额和进口总额,则可以把它们表示在同一幅统计图中,绘制复合折线图或复合条形图.
新课讲解
4. 下表是2013—2022年我国货物出口总额与进口总额的数据.请选择合适的统计图,描述这十年我国货物进、出口总额的变化情况,并对它们进行比较.
例
解:可以绘制复合折线图,也可以绘制复合条形图描述上表中的数据,如图所示.
从复合折线图或复合条形图中可以看出,除2014、2015、2016年外,2013—2022年这十年间,我国的货物出口总额与进口总额基本上都保持逐年增长的趋势,而且每年的出口总额都大于进口总额.
新课讲解
例
5. 小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C 三种品牌电视机销售情况的有关数据统计如图 ①②③ .
根据上述三个统计图,请解答:
(1)2019-2024 年三种品牌电视机销售总量最多的是 ______品牌,2024 年比 2023 年 A 品牌月平均销售量的增长率为_______ .
B
16%
(2)2024 年其他品牌的电视机年销售总量是多少万台?
解:(20 × 12) ÷ 25 % = 960(万台),1-25%-29%-34%=12%,960×12%=115.2(万台) .
答:2024 年其他品牌的电视机年销售总量是 115.2 万台 .
新课讲解
例
5. 小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C 三种品牌电视机销售情况的有关数据统计如图 ①②③ .
根据上述三个统计图,请解答:
(3)货比三家后,你建议小聪家购买哪种品牌的电视机?说说你的理由 .
解:因为 B 品牌 2024 年的市场占有率最高,且 6 年的月销售量最稳定,所以建议购买 B 品牌 (答案不唯一)
新课讲解
练一练
第五代移动通信技术(简称 5G)是最新
一代蜂窝移动通信技术,5G 移动通信将
推动我国数字经济发展迈上新台阶 . 据预
测,2020年到 2025 年中国 5G 直接经济产
出和间接经济产出的情况如图所示 .根提图中提供的信息回答下列问题 .
(1)2020 年到 2025 年,求 5G 间接经济产出总量共多少万亿元;
解:(1) 2020年到2025年,5G间接经济产出总量共为1.2+2+4+5+6+6.3=24.5(万亿元).
(2)2020 年到 2025 年,求 5G 间接经济产出总量比直接经济产出总量多多少万亿元;
(2) 2020年到2025年5G直接经济产出总量为0.5+1+2+2.5+3+3.3=12.3(万亿元),
∴2020年到2025年,5G间接经济产出总量比直接经济产出总量多24.5-12.3=12.2(万亿元).
新课讲解
练一练
第五代移动通信技术(简称 5G)是最新
一代蜂窝移动通信技术,5G 移动通信将
推动我国数字经济发展迈上新台阶 . 据预
测,2020年到 2025 年中国 5G 直接经济产
出和间接经济产出的情况如图所示 .根提图中提供的信息回答下列问题 .
(3)下面的推断合理的是 ______(只填序号) .
① 2020 年到 2025 年,5G 间接经济产出和直接经济产出都呈增长趋势;
② 2023 年到 2024 年,5G 间接经济产出和直接经济产出的增长率相同 .
①②
课堂小结
复和
条形图
复和条形图能清楚地表示各部分的具体数量,便于直观地对不同组别或类别的数据进行比较.
复和
折线图
复和折线图主要用于表示多组数据的增减变化情况,有利于描述多组数据的发展趋势.
复和统计图
特点
绘制扇形图的一般步骤
(1)算:计算各部分在总体中所占的百分比.
(2)求:求各部分对应扇形的圆心角的度数,即360°×各部分占总体的百分比.
(3)画:取适当的半径画圆,利用量角器作出各圆心角,从而在圆内画出各个扇形.
(4)标:在相应的扇形上注明各部分的名称及其相应的百分比.
扇形图
用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
当堂小练
1. 如图 是小张同学某一天的作息时间扇形统计图,则下列说法正确的是( )
A. 小张的睡眠时间占全天时间的 45%
B. 小张的体育活动时间为 2 小时
C. 小张的课业学习时间最多
D. 小张的睡眠时间为 8.4 小时
解:由扇形统计图,得
小张的睡眠时间占全天时间的百分比为 1-30%-10%-10%-15%=35%.
小张的体育活动时间为 24×10%=2.4(小时).
∵ 小张的睡眠时间占全天时间的 35%,
∴ 小张的睡眠时间最多.
小张的睡眠时间为 24×35%=8.4(小时).
D
当堂小练
2. 一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图,若最喜爱足球的人数比最喜爱游泳的人数多 20 人,则这次问卷调查的总人数为_______ .
200
当堂小练
2. 为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班 50 名同学进行了问卷调查(每名同学只选其中的一类),依据 50 份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图如图所示.下列说法正确的是( )
A. 班主任采用的是抽样调查
B. 喜爱动画节目的同学最多
C. 喜爱戏曲节目的同学有 6 名
D“体育”对应扇形的圆心角为 72°
D
解:班主任采用的是全面调查,故选项 A 说法错误,不符合题意;
喜爱娱乐节目的同学最多,故选项B 说法错误,不符合题意;
喜爱戏曲节目的同学有 50×6%=3(名),故选项 C 说法错误,不符合题意;
“体 育”对 应 扇 形 的 圆 心 角 为360 × 20%=72 ,故 选 项 D 说 法 正确,符合题意 .
当堂小练
3. 如图 ,观察扇形统计图,并回答下列问题:
(1)如果用这个圆代表总体,那么扇形____表示总体的45%;
(2)如果用这个圆表示某班级的全体40人,那么扇形 B 代表 ____人;
(3)如 果 用 这 个 圆 代 表 9 km2 的 稻 田,那 么 扇 形 A 代表____ km2;
(4)如果用这个圆代表某校全体学生的人数,已知扇形 B比扇形 A 代表的人数多 60,那么全校共有学生 _____人 .
C
12
2.25
1 200
解:(1) 如果用这个圆代表总体,易知扇形 A 表示总体的 25%,则扇形 C 表示总体的1-25%-30%=45%.
(2) 40×30%=12(人),故扇形 B 代表 12 人 .
(3) 9× =2.25(km 2), 故扇形 A 代表 2.25 km 2.
(4) 60÷ 30% - =1 200(人),故全校共有学生 1 200 人 .
当堂小练
4. 下面是某地区7~15岁男生、女生平均身高统计表.
(1) 要描述男生与女生身高变化情况,你认为选择______统计图比较合适.
(2) 请在下图中画出你选择的统计图,并写出标题,给出图例.
折线
如图所示
当堂小练
(3) 观察(2)中所画统计图,你能得出什么结论?
(4) 你还能提出什么数学问题?并给出答案.
解:(3)(答案不唯一)从折线图中可以发现,男生在12~15岁身体发育较女生迅速.
(4)(答案不唯一)问题:男生在12~15岁身体发育较女生迅速,应注意什么问题?
答:应注意加强营养和心理疏导.
当堂小练
5. 在社会课上学习了《中国的地形分布》一课后,小雨对自己家乡宁波的地形分布情况产生了浓厚的兴趣 . 在翻阅查找了大量的文献资料后,小雨根据所获得的宁波市陆域地形分布数据,制作了如图两个不完整的统计图 .
根据以上信息,回答下列问题:
(1)根据上述材料,宁波市的陆域总面积是______km2.
解:(1) 宁波市的陆域总面积是 2 450÷25%=9 800 (km 2) .
9 800
(2)请计算宁波市的平原地形的面积,并补全条形统计图 .
(3)在扇形统计图中,求台地对应扇形的圆心角度数.
(2) 平原地形的面积为9 800×40%=3 920 (km 2) .
补全条形统计图如图所示.
(3) 360× =7.2 ,
∴ 台地对应扇形的圆心角度数为 7.2 .
对接中考
1. 如图显示了某地连续5天的日最低气温,则能表示这5天日最低气温变化情况的是( )
A. B.
C. D.
A
对接中考
2. 为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班50名同学进行了问卷调查(每名同学只选其中的一类),依据50份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图(如图所示).下列说法正确的是( )
A.班主任采用的是抽样调查
B.喜爱动画节目的同学最多
C.喜爱戏曲节目的同学有6名
D.“体育”对应扇形的圆心角为72°
D
对接中考
3. 2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图,则a的值为 .若将获奖作品按四个等级所占比例绘制成扇形统计图,则“一等奖”对应扇形的圆心角度数为 .
30
36°
对接中考
4. 2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑.某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为A,B,C,D四个等级(A:非常了解;B:比较了解;C:了解;D:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.根据统计图信息,下列结论不正确的是( )
A.样本容量是200
B.样本中C等级所占百分比是10%
C.D等级所在扇形的圆心角为15°
D.估计全校学生A等级大约有900人
C
拓展与延伸
某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A 篮球,B 足球,C 排球,D 羽毛球,E 乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
200
36°
(1) 本次调查的样本容量是 ,扇形统计图中C对应圆心角的度数为 ;
(2) 请补全条形统计图;
B项目的人数为:200﹣54﹣20﹣50﹣46=30.
30
(3) 若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
∵ (名),∴该校最喜欢“E乒乓球”的学生人数约为460名.
第十二章 数据的收集、整理与描述
12.2 用统计图描述数据
12.2.1 扇形图、条形图和折线图
目
录
1. 学习目标
4. 知识点1 扇形统计图
7. 课堂小结
8. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 条形图和折线图
10. 拓展与延伸
9. 对接中考
3. 新课导入
6. 知识点3 条形图和折线图
1. 会绘制扇形图,能读懂扇形图、条形图、折线图反映的数据信息.
2. 能清晰认识不同统计图之间的差异与联系;在实际应用中能准确选择合适的统计图,培养数据分析能力.
3. 能用扇形图、条形图、折线图整理与描述收集到的数据,能根据统计图表分析随机现象的变化趋势,体会数据分析的必要性,形成数据观念.
学习目标
知识回顾
数据的收集
数据的整理
统计调查
全面调查
抽样调查
总体:所要考察的全体对象
个体:组成总体的每一个考察对象
样本:从总体中所抽取的一部分个体
样本容量:样本中包含的个体的数目
数据的描述
数据的分析
统计表
统计图
用样本估计总体
新课导入
条形图
扇形图
折线图
直方图
趋势图
新课讲解
知识点1 扇形统计图
【问题】 如何绘制扇形图?
文学
科技
体育
艺术
劳技
14%
16%
34%
28%
8%
新课讲解
绘制扇形图的步骤:
1. 算:根据各部分占总体的百分比.
2. 求:求各部分对应扇形的圆心角的度数,即360°×各部分占总体的百分比.
3. 画:取适当的半径画圆,利用量角器作出各圆心角,在圆内画出各个扇形.
4. 标:在相应的扇形上注明各类别的名称及其相应的百分比.
扇形图用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
新课讲解
1. 某学校对全校500名学生进行了一项关于课外阅读偏好的调查,结果如下:喜欢读文学类书籍的学生有150名,喜欢读科普类书籍的学生有100名,喜欢读历史类书籍的学生有80名,喜欢读漫画类书籍的学生有60名,其余的学生则没有特定的阅读偏好.
(1)请根据以上数据,绘制一个扇形图;
解:(1)喜欢读文学类书籍的学生所占百分比=×100%=30%;
喜欢读科普类书籍的学生所占百分比=×100%=20%;
喜欢读历史类书籍的学生所占百分比= ×100%=16%;
喜欢读漫画类书籍的学生所占百分比=×100%=12%;
没有特定阅读偏好的学生所占百分比=100%-(30%+20%+ 16%+12%)=22%.
例
喜欢读文学类、科普类、历史类、漫画类及没有特定阅读偏好类所在扇形的圆心角度数依次为360°×30%=108°,360°×20%=72°, 360°×16%=57.6°,360°×12%=43.2°,360°×22%=79.2°.
画扇形图如图所示.
新课讲解
1. 某学校对全校500名学生进行了一项关于课外阅读偏好的调查,结果如下:喜欢读文学类书籍的学生有150名,喜欢读科普类书籍的学生有100名,喜欢读历史类书籍的学生有80名,喜欢读漫画类书籍的学生有60名,其余的学生则没有特定的阅读偏好.
(2)没有特定阅读偏好的学生有多少名?
例
画扇形图如图所示.
解:(2)因为没有特定阅读偏好的学生所占的百分比是22%,
所以没有特定阅读偏好的学生有500×22%=110(名).
新课讲解
练一练
1. 一所中学准备搬迁到新校舍,在迁校舍前对该校 300名学生如何到新校舍进行了一次调查,调查结果如下表.
请你根据表中数据画出表示调查结果的扇形统计图.
步行 骑自行车 乘公交车 其他
60 人 105 人 120 人 15 人
解:各部分占总体的百分比分别为:
步行:60÷300=20%,
骑自行车:105÷300=35%,
乘公交车:120÷300=40%,
其他:15÷300 = 5%.
所 对 应 扇 形 圆 心 角 的 度 数 分 别 为
360°× 20%=72° ,360°× 35%=126° ,
360°× 40%=144° ,360°× 5%=18° .
扇形统计图如图 所示 .
新课讲解
练一练
2. 某电视台“市民热线”对上个月内接到的热线电话进行了分类统计,部分数据如表:
(1)将表格补充完整 .
类型 热线电话数量/ 个 百分比
城建 30 10%
环保 _____ _____
道路交通 ____ 20%
其他方面 ____ 10%
解:30÷10%=300(个),300×20%=60(个),
300×10%=30(个),1-10%-20%-10%=60%,
300×60%=180(个).
180
60%
60
30
新课讲解
练一练
2. 某电视台“市民热线”对上个月内接到的热线电话进行了分类统计,部分数据如表:
(2)在扇形统计图中,各类数据对应的圆心角分别是多少度?.
(3)画出扇形统计图,标上各类型相应的百分比,并写上统计图的名称.
解:(2)在扇形统计图中,“城建”对应的圆心角度数为360×10%=36,
“环保”对应的圆心角度数为360×60%=216,
“道路交通”对应的圆心角度数为360×20%=72,
“其他方面”对应的圆心角度数为360×10%=36.
(3)画出扇形统计图如图.
电视台“市民热线”上个月内接到的热线电话类型扇形统计图
新课讲解
知识点2 条形图和折线图
条形图 扇形图 折线图
图示
新课讲解
条形图 扇形图 折线图
特点 用一个单位长度表示一定的数量 , 用宽度相同的直条的高低表示数量的多少 用整个圆表示总体,用圆内的每个扇形表示总体中的一部分,通过扇形的大小反映各个部分占总体的百分比 用一个单位长度表示一定的数量 , 用折线的起伏表示数量的增减变化
优点 能清楚地表示各部分的具体数量,便于相互比较 能清楚地表示各部分在总体中所占的百分比 能清楚地看出数量增减变化的情况 , 也能看出各部分数量的多少
缺点 不能反映各部分占总体的百分比 不能反映各部分数量的多少 不能反映各部分占总体的百分比
选用情境 比较数据之间的大小关系 表示各部分占总体的百分比 表示数据的变化趋势
1. 在同一条形图中,小长方形的宽必须相同;
2. 利用折线图比较两个统计量的变化趋势时,纵轴上同一单位长度所表示的意义必须要一致 .
注意
新课讲解
例
2. 体重指数(BMI)是衡量人体胖瘦程度的常用指标( ).某公司为了解员工的胖瘦状况,随机抽取了60名员工的体检数据,计算得到他们的体重指数数据 (单位:kg/m2),如表所示. 请选择合适的统计图,表示这个公司60名员工中各类别体重指数的员工人数和所占的百分比.同时说一说从绘制的统计图中,能获得哪些信息.
分析:可以先借助表格,统计各类别体重指数的员工人数和所占的百分比.
为了清楚地表示各类别中的人数,可以绘制条形图;为了直观地表示各类别中的人数所占的百分比,可以绘制扇形图.
新课讲解
解:根据上表中的数据,统计出这个公司60名员工的体重指数情况, 如下表所示.
分别画出条形图和扇形图,表示这个公司各类别体重指数的员工人数和所占的百分比.
新课讲解
从条形图和扇形图中可以看出,这个公司60名员工中体重正常的人数最多,有38人,所占百分比为63.3%;体重过低的人数次之,有10人,所占百分比为16.7%;超重的有7人,所占百分比为11.7%;肥胖的人数最少,有5人,所占百分比为8.3%.
由此可以推断这个公司员工的胖瘦状况.
例如,这个公司大多数员工的体重正常,但仍有大约8%的员工肥胖,需要引起注意.
新课讲解
3. 某平台发布《2024 春节档电影数据洞察报告》数据显示,春节档电影总票房创历史新高.春节档 8 天日票房收入及票房冠军电影 A 在日票房收入中所占比重分别如左图和右图所示.
例
【数据分析】
(1)下列结论中,所有正确的序号是 ________.
①初一至初八日票房收入超过 10 亿的天数占 50%;
②初一至初八电影 A 票房在日票房收入中所占比重呈先上升再下降的趋势;
③电影 A 日票房收入最高的一天是初四.
①②
新课讲解
3. 某平台发布《2024 春节档电影数据洞察报告》数据显示,春节档电影总票房创历史新高.春节档 8 天日票房收入及票房冠军电影 A 在日票房收入中所占比重分别如左图和右图所示.
例
(2)2024 春节档 8 天微博电影相关热搜总数为 946 个,将微博映后热搜类型分布、各级城市票房收入占比和观众性别占比绘制成如图 ①②③.
①求“全民讨论”的热搜个数(精确到个位).
②结合各级城市票房收入占比和观众性别占比分析,如果你是投资方,来年的春节档你投资影片会考虑哪些因素?
解:①“全民讨论”的热搜个数约为 946×57.3% ≈ 542(个) .
②由题意知四线城市占比最多,女性观众占比高于男性观众,∴ 来年的春节档投资影片会考虑女性观众的视角,投资反应社会上女性在生活、工作时真实现状的影片,在四线城市加大投放量.(合理即可)
新课讲解
练一练
1. 某公司调查某中学学生对其环保产品的了解情况,随机抽取该校部分学生进行问卷,结果分“非常了解”“比较了解”“一般了解”“不了解”四种类型,分别记 为 A, B, C, D,根据调查结果绘制了如下尚不完整的扇形统计图 .
(1)本次问卷共随机调查了___ 名学生,在扇形统计图中, m=___.
(2)请根据数据信息,补全条形统计图 .
50
32
解:A类型的人数为50×16%=8,补全条形统计图如图.
(3)若该校有 1000名学生,估计选择“非常了解”“比较了解” 的学生共有多少名?
解:1 000×(16%+40%)=560(名),
答:估计选择“非常了解”“比较了解”的学生共有560名.
新课讲解
练一练
2. 七年级的所有学生都参加了社团活动,因条件限制,每名学生都只能加入一个社团. 李明对全年级同学参加社团活动的情况进行了一次调查.如图是根据李明的调查数据绘制的不完整的统计图,请根据图中信息,回答下列问题,并将统计图补充完整.
(1) 七年级共有多少名学生?
解:∵80÷40%=200(名),
∴七年级共有200名学生.
(2) 七年级有多少名学生参加篮球社?
解:∵200×10%=20(名),
∴七年级有20名学生参加篮球社.
新课讲解
练一练
2. 七年级的所有学生都参加了社团活动,因条件限制,每名学生都只能加入一个社团. 李明对全年级同学参加社团活动的情况进行了一次调查.如图是根据李明的调查数据绘制的不完整的统计图,请根据图中信息,回答下列问题,并将统计图补充完整.
(3) 七年级参加美术社的学生人数占全年级总人数的百分比是多少?
解:∵×100%=30%, ∴七年级参加美术社的学生人数占全年级总人数的30%.
(4) 将统计图补充完整.
解:统计图补充如图所示:
20
新课讲解
知识点3 复合折线图、复合条形图
4. 下表是2013—2022年我国货物出口总额与进口总额的数据.请选择合适的统计图,描述这十年我国货物进、出口总额的变化情况,并对它们进行比较.
例
分析:折线图用折线的上升或下降表示数据的增减变化情况,有利于描述数据的发展趋势;条形图能直观地表示各个数据的大小,便于比较数据.因此,可以绘制折线图或条形图描述这十年我国货物进、出口总额各自的变化情况.而要比较货物出口总额和进口总额,则可以把它们表示在同一幅统计图中,绘制复合折线图或复合条形图.
新课讲解
4. 下表是2013—2022年我国货物出口总额与进口总额的数据.请选择合适的统计图,描述这十年我国货物进、出口总额的变化情况,并对它们进行比较.
例
解:可以绘制复合折线图,也可以绘制复合条形图描述上表中的数据,如图所示.
从复合折线图或复合条形图中可以看出,除2014、2015、2016年外,2013—2022年这十年间,我国的货物出口总额与进口总额基本上都保持逐年增长的趋势,而且每年的出口总额都大于进口总额.
新课讲解
例
5. 小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C 三种品牌电视机销售情况的有关数据统计如图 ①②③ .
根据上述三个统计图,请解答:
(1)2019-2024 年三种品牌电视机销售总量最多的是 ______品牌,2024 年比 2023 年 A 品牌月平均销售量的增长率为_______ .
B
16%
(2)2024 年其他品牌的电视机年销售总量是多少万台?
解:(20 × 12) ÷ 25 % = 960(万台),1-25%-29%-34%=12%,960×12%=115.2(万台) .
答:2024 年其他品牌的电视机年销售总量是 115.2 万台 .
新课讲解
例
5. 小聪家准备购买一台电视机,小聪将收集到的某地区A,B,C 三种品牌电视机销售情况的有关数据统计如图 ①②③ .
根据上述三个统计图,请解答:
(3)货比三家后,你建议小聪家购买哪种品牌的电视机?说说你的理由 .
解:因为 B 品牌 2024 年的市场占有率最高,且 6 年的月销售量最稳定,所以建议购买 B 品牌 (答案不唯一)
新课讲解
练一练
第五代移动通信技术(简称 5G)是最新
一代蜂窝移动通信技术,5G 移动通信将
推动我国数字经济发展迈上新台阶 . 据预
测,2020年到 2025 年中国 5G 直接经济产
出和间接经济产出的情况如图所示 .根提图中提供的信息回答下列问题 .
(1)2020 年到 2025 年,求 5G 间接经济产出总量共多少万亿元;
解:(1) 2020年到2025年,5G间接经济产出总量共为1.2+2+4+5+6+6.3=24.5(万亿元).
(2)2020 年到 2025 年,求 5G 间接经济产出总量比直接经济产出总量多多少万亿元;
(2) 2020年到2025年5G直接经济产出总量为0.5+1+2+2.5+3+3.3=12.3(万亿元),
∴2020年到2025年,5G间接经济产出总量比直接经济产出总量多24.5-12.3=12.2(万亿元).
新课讲解
练一练
第五代移动通信技术(简称 5G)是最新
一代蜂窝移动通信技术,5G 移动通信将
推动我国数字经济发展迈上新台阶 . 据预
测,2020年到 2025 年中国 5G 直接经济产
出和间接经济产出的情况如图所示 .根提图中提供的信息回答下列问题 .
(3)下面的推断合理的是 ______(只填序号) .
① 2020 年到 2025 年,5G 间接经济产出和直接经济产出都呈增长趋势;
② 2023 年到 2024 年,5G 间接经济产出和直接经济产出的增长率相同 .
①②
课堂小结
复和
条形图
复和条形图能清楚地表示各部分的具体数量,便于直观地对不同组别或类别的数据进行比较.
复和
折线图
复和折线图主要用于表示多组数据的增减变化情况,有利于描述多组数据的发展趋势.
复和统计图
特点
绘制扇形图的一般步骤
(1)算:计算各部分在总体中所占的百分比.
(2)求:求各部分对应扇形的圆心角的度数,即360°×各部分占总体的百分比.
(3)画:取适当的半径画圆,利用量角器作出各圆心角,从而在圆内画出各个扇形.
(4)标:在相应的扇形上注明各部分的名称及其相应的百分比.
扇形图
用圆代表总体,每一个扇形代表总体中的一部分,通过扇形的大小反映各个部分占总体的百分比.
当堂小练
1. 如图 是小张同学某一天的作息时间扇形统计图,则下列说法正确的是( )
A. 小张的睡眠时间占全天时间的 45%
B. 小张的体育活动时间为 2 小时
C. 小张的课业学习时间最多
D. 小张的睡眠时间为 8.4 小时
解:由扇形统计图,得
小张的睡眠时间占全天时间的百分比为 1-30%-10%-10%-15%=35%.
小张的体育活动时间为 24×10%=2.4(小时).
∵ 小张的睡眠时间占全天时间的 35%,
∴ 小张的睡眠时间最多.
小张的睡眠时间为 24×35%=8.4(小时).
D
当堂小练
2. 一次对若干名青少年进行最喜爱的运动项目的问卷调查,得到如图的统计图,若最喜爱足球的人数比最喜爱游泳的人数多 20 人,则这次问卷调查的总人数为_______ .
200
当堂小练
2. 为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班 50 名同学进行了问卷调查(每名同学只选其中的一类),依据 50 份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图如图所示.下列说法正确的是( )
A. 班主任采用的是抽样调查
B. 喜爱动画节目的同学最多
C. 喜爱戏曲节目的同学有 6 名
D“体育”对应扇形的圆心角为 72°
D
解:班主任采用的是全面调查,故选项 A 说法错误,不符合题意;
喜爱娱乐节目的同学最多,故选项B 说法错误,不符合题意;
喜爱戏曲节目的同学有 50×6%=3(名),故选项 C 说法错误,不符合题意;
“体 育”对 应 扇 形 的 圆 心 角 为360 × 20%=72 ,故 选 项 D 说 法 正确,符合题意 .
当堂小练
3. 如图 ,观察扇形统计图,并回答下列问题:
(1)如果用这个圆代表总体,那么扇形____表示总体的45%;
(2)如果用这个圆表示某班级的全体40人,那么扇形 B 代表 ____人;
(3)如 果 用 这 个 圆 代 表 9 km2 的 稻 田,那 么 扇 形 A 代表____ km2;
(4)如果用这个圆代表某校全体学生的人数,已知扇形 B比扇形 A 代表的人数多 60,那么全校共有学生 _____人 .
C
12
2.25
1 200
解:(1) 如果用这个圆代表总体,易知扇形 A 表示总体的 25%,则扇形 C 表示总体的1-25%-30%=45%.
(2) 40×30%=12(人),故扇形 B 代表 12 人 .
(3) 9× =2.25(km 2), 故扇形 A 代表 2.25 km 2.
(4) 60÷ 30% - =1 200(人),故全校共有学生 1 200 人 .
当堂小练
4. 下面是某地区7~15岁男生、女生平均身高统计表.
(1) 要描述男生与女生身高变化情况,你认为选择______统计图比较合适.
(2) 请在下图中画出你选择的统计图,并写出标题,给出图例.
折线
如图所示
当堂小练
(3) 观察(2)中所画统计图,你能得出什么结论?
(4) 你还能提出什么数学问题?并给出答案.
解:(3)(答案不唯一)从折线图中可以发现,男生在12~15岁身体发育较女生迅速.
(4)(答案不唯一)问题:男生在12~15岁身体发育较女生迅速,应注意什么问题?
答:应注意加强营养和心理疏导.
当堂小练
5. 在社会课上学习了《中国的地形分布》一课后,小雨对自己家乡宁波的地形分布情况产生了浓厚的兴趣 . 在翻阅查找了大量的文献资料后,小雨根据所获得的宁波市陆域地形分布数据,制作了如图两个不完整的统计图 .
根据以上信息,回答下列问题:
(1)根据上述材料,宁波市的陆域总面积是______km2.
解:(1) 宁波市的陆域总面积是 2 450÷25%=9 800 (km 2) .
9 800
(2)请计算宁波市的平原地形的面积,并补全条形统计图 .
(3)在扇形统计图中,求台地对应扇形的圆心角度数.
(2) 平原地形的面积为9 800×40%=3 920 (km 2) .
补全条形统计图如图所示.
(3) 360× =7.2 ,
∴ 台地对应扇形的圆心角度数为 7.2 .
对接中考
1. 如图显示了某地连续5天的日最低气温,则能表示这5天日最低气温变化情况的是( )
A. B.
C. D.
A
对接中考
2. 为了解全班同学对新闻、体育、动画、娱乐、戏曲五类节目的喜爱情况,班主任对全班50名同学进行了问卷调查(每名同学只选其中的一类),依据50份问卷调查结果绘制了全班同学喜爱节目情况扇形统计图(如图所示).下列说法正确的是( )
A.班主任采用的是抽样调查
B.喜爱动画节目的同学最多
C.喜爱戏曲节目的同学有6名
D.“体育”对应扇形的圆心角为72°
D
对接中考
3. 2023年5月30日是第7个全国科技工作者日,某中学举行了科普知识手抄报评比活动,共有100件作品获得一、二、三等奖和优胜奖,根据获奖结果绘制如图所示的条形图,则a的值为 .若将获奖作品按四个等级所占比例绘制成扇形统计图,则“一等奖”对应扇形的圆心角度数为 .
30
36°
对接中考
4. 2023年5月30日,神舟十六号载人飞船成功发射,成为我国航天事业的里程碑.某校对全校1500名学生进行了“航空航天知识”了解情况的调查,调查结果分为A,B,C,D四个等级(A:非常了解;B:比较了解;C:了解;D:不了解).随机抽取了部分学生的调查结果,绘制成两幅不完整的统计图.根据统计图信息,下列结论不正确的是( )
A.样本容量是200
B.样本中C等级所占百分比是10%
C.D等级所在扇形的圆心角为15°
D.估计全校学生A等级大约有900人
C
拓展与延伸
某校为丰富学生的课余生活,开展了多姿多彩的体育活动,开设了五种球类运动项目:A 篮球,B 足球,C 排球,D 羽毛球,E 乒乓球.为了解学生最喜欢以上哪种球类运动项目,随机抽取部分学生进行调查(每位学生仅选一种),并绘制了统计图.某同学不小心将图中部分数据丢失,请结合统计图,完成下列问题:
200
36°
(1) 本次调查的样本容量是 ,扇形统计图中C对应圆心角的度数为 ;
(2) 请补全条形统计图;
B项目的人数为:200﹣54﹣20﹣50﹣46=30.
30
(3) 若该校共有2000名学生,请你估计该校最喜欢“E乒乓球”的学生人数.
∵ (名),∴该校最喜欢“E乒乓球”的学生人数约为460名.
同课章节目录
