12.2.2 直方图 课件(共43张PPT)
文档属性
| 名称 | 12.2.2 直方图 课件(共43张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 10:49:54 | ||
图片预览








文档简介
(共43张PPT)
第十二章 数据的收集、整理与描述
12.2 用统计图描述数据
12.2.2 直方图
目
录
1. 学习目标
4. 知识点1 频数分布表
7. 课堂小结
8. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 频数分布直方图
9. 对接中考
3. 新课导入
6. 知识点3 频数分布直方图的应用
1.理解频数分布直方图及其相关概念;会制作频数分布表;会画频数分布直方图.
2.能利用直方图描述数据,能够从直方图中获取相关信息,培养数据分析能力,并解决实际问题.
学习目标
知识回顾
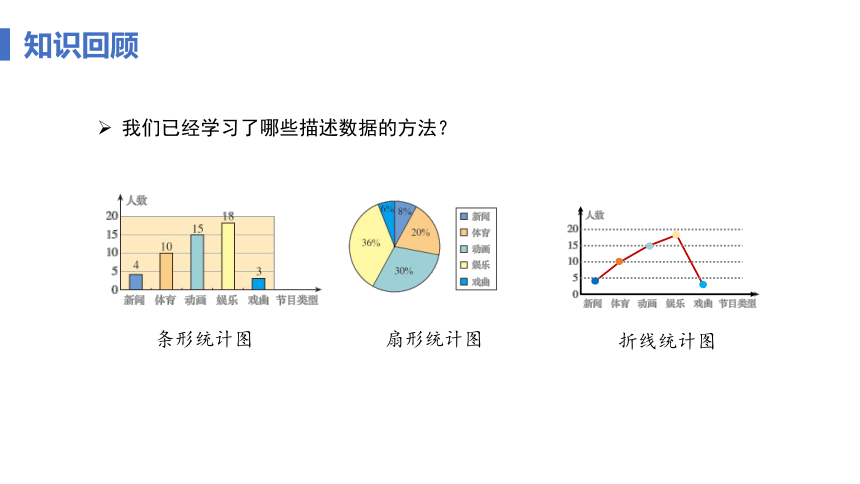
我们已经学习了哪些描述数据的方法?
扇形统计图
条形统计图
折线统计图
新课导入
我们已经学习过了条形图、折线图、扇形图等描述数据的方法,本节我们将学习另一种常用来描述数据的统计图——直方图.
新课讲解
知识点1 频数分布表
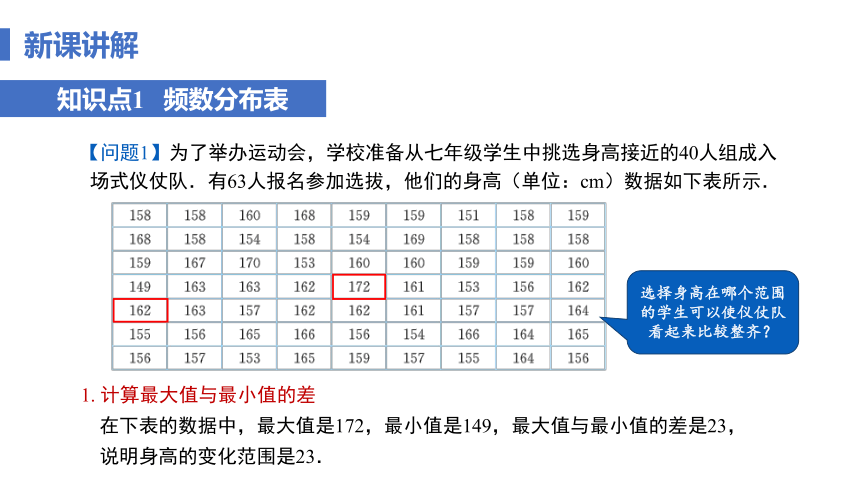
【问题1】为了举办运动会,学校准备从七年级学生中挑选身高接近的40人组成入场式仪仗队.有63人报名参加选拔,他们的身高(单位:cm)数据如下表所示.
选择身高在哪个范围的学生可以使仪仗队看起来比较整齐?
1. 计算最大值与最小值的差
在下表的数据中,最大值是172,最小值是149,最大值与最小值的差是23,说明身高的变化范围是23.
新课讲解
2. 决定组距和组数
把所有数据分成若干组,每个小组的两个端点间的距离 (组内数据的取值范围)称为组距.根据问题的需要,各组的组距可以相同或不同.
在本问题中, 我们作等距分组,即令各组的组距相同.
②数据分组:(x表示身高值)
149≤x<152,
152≤x<155,
…,
170≤x<173.
①组距与组数
组距为3
组数为8
当数据在100个以内时,按照数据的多少,常分成5~12组.
新课讲解
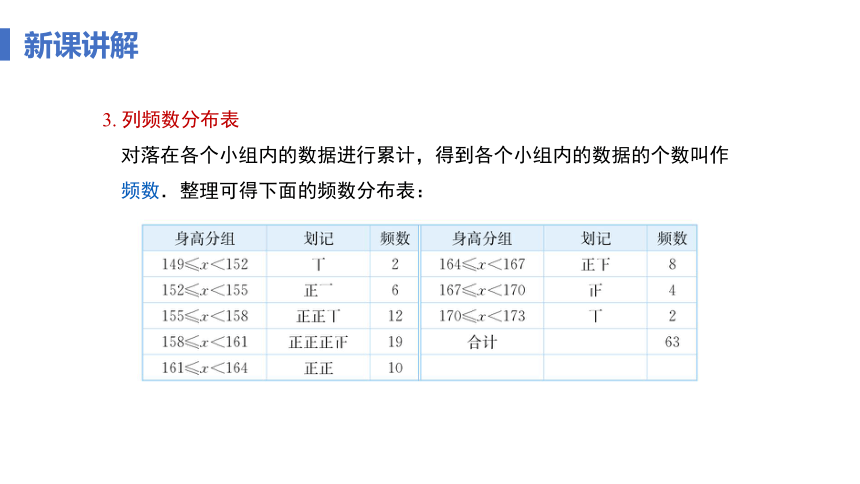
3. 列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数叫作频数.整理可得下面的频数分布表:
新课讲解
1. 各小组的频数之和等于总数;
2. 组距可以相同,也可以不同;为研究方便,本节中我们作等距分组;
3. 数据所分组数没有明确要求,当数据在100 个以内时,根据数据的多少,常分成5 ~ 12 组.
数据分组时,可以先确定组距,再根据组距确定组数;也可以先确定组数,再根据组数确定组距 .
注意
新课讲解
频数分布表制作步骤
1. 算:计算最大值与最小值的差,得到数据的变化范围.
2. 定:根据数据的个数与数据的变化范围,确定组距、组数.
3. 划:利用划记的方法累计落在各组内的数据个数,得到各组的频数.
4. 列:根据上述过程列频数分布表. 频数分布表一般由数据分组、划记、频数三部分组成.
归纳
新课讲解
例
1. 有60 个数据,其中最大的数据是187,最小的数据是140,如果分组时的组距为6,那么这组数据应分为( )
A. 7 组 B. 7 组 C. 8 组 D. 10 组
解:因为 =7,所以这组数据应分为8 组.
C
新课讲解
例
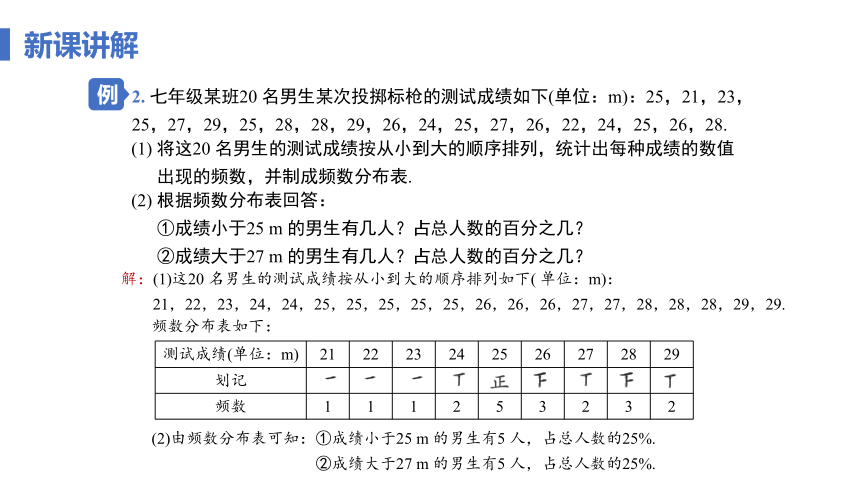
2. 七年级某班20 名男生某次投掷标枪的测试成绩如下(单位:m):25,21,23,25,27,29,25,28,28,29,26,24,25,27,26,22,24,25,26,28.
(1) 将这20 名男生的测试成绩按从小到大的顺序排列,统计出每种成绩的数值出现的频数,并制成频数分布表.
解:(1)这20 名男生的测试成绩按从小到大的顺序排列如下( 单位:m):
21,22,23,24,24,25,25,25,25,25,26,26,26,27,27,28,28,28,29,29.
频数分布表如下:
测试成绩(单位:m) 21 22 23 24 25 26 27 28 29
划记
频数 1 1 1 2 5 3 2 3 2
(2) 根据频数分布表回答:
①成绩小于25 m 的男生有几人?占总人数的百分之几?
②成绩大于27 m 的男生有几人?占总人数的百分之几?
(2)由频数分布表可知:①成绩小于25 m 的男生有5 人,占总人数的25%.
②成绩大于27 m 的男生有5 人,占总人数的25%.
新课讲解
练一练
1. 已知样本 21,21,22,23,24,25,25,25,26,26,26,27,28,29,29,30. 若组距为 2,那么组数是____________.
5
新课讲解
练一练
2. 某校学生会为了了解全校学生对艺体项目的喜爱情况,随机调查了200 名学生(每名学生仅选一项最喜爱的项目),根据调查结果制作了如下频数分布表:
最喜爱的项目 频数 百分比
篮球 28%
排球 24 12%
乒乓球 48 24%
健美操
武术操 22 11%
跑步 20 10%
合计 200 1
(1)补全频数分布表.
56
30
15%
(2)在这次抽样调查中,最喜爱哪个项目的学生最多?最喜爱哪个项目的学生最少?
解:(2) 最喜爱篮球的学生最多,最喜爱跑步的学生最少.
(3)根据以上调查,试估计该校1620 名学生中最喜爱健美操的有多少名.
(3) 估计该校1620名学生中最喜爱健美操的有1620×15%=243(名).
新课讲解
知识点2 频数分布直方图
4. 画频数分布直方图
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小,小长方形的高是频数与组距的比值.
为了更直观形象地看出频数分布的情况,可以根据频数分布表画出频数分布直方图.
画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
小长方形的宽是组距
小长方形的高是频数与组距的比值
横轴
纵轴
新课讲解
从频数分布表和频数分布直方图中可以看出,身高在155≤x<158,158≤x<161, 161≤x<164三个组的人数最多,共有12+19+10=41(人).因此,可以从身高在155 cm至164 cm(不含164 cm)范围的同学中挑选仪仗队队员.
新课讲解
画频数分布直方图的基本步骤
1. 算:计算最大值与最小值的差,确定数据值的变化范围.
2. 定:决定组距和组数,当数据在100个以内时,按照数据的多少,常分成5~12组.
3. 列:列频数分布表.
4. 画:画频数分布直方图.
归纳
新课讲解
画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
1. 直方图中的各小长方形之间没有空隙;
2. 一般情况下,相邻各分点的归宿:“上限不在内”.
新课讲解
等距分组的频数分布直方图的画法.
1. 画两条互相垂直的轴:横轴和纵轴;
2. 在横轴上划分一些相互衔接的线段,每条线段表示一组,在每条线段的左端点标明这组的下限,在线段的右端点标明其上限;
3. 在纵轴上划分刻度,并用自然数标记;
4. 以横轴上的每条线段为底各作一个长方形立于横轴上,使各长方形的高等于相应的频数.
新课讲解
直方图与条形图的区别
条形图 直方图
用小长方形的高度表示数据的大小 以小长方形的面积来表示频数的大小
横轴上的数据是孤立的,相邻的数据没有联系 横轴上相邻的数据有必然联系,它表示一个范围
各个小长方形之间有间隔 相邻的小长方形之间没有间隔
侧重反映每个项目具体数目的多少 描述的是一组连续的数据,它侧重反映这些数据落在各小组内的频数的分布情况
新课讲解
例
3. 某中学部分同学参加数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分为120 分),
并且绘制了如图所示的频数分布直方图(每组中含
最低分数,但不含最高分数),请回答:
(1)该中学参加本次数学竞赛的共有多少人?
(2)如果成绩在90分以上(含90 分)的同学获奖,那么该中学参赛同学的获奖率是多少?
解:由频数分布直方图知,从左到右各分数段的人数分别为4,6,8,7,5,2.
(1) 4+6+8+7+5+2=32(人). 所以该中学参加本次数学竞赛的共有32 人.
(2) 成绩在90 分以上(含90 分)的同学有7+5+2=14(人),
所以该中学参赛同学的获奖率是 ×100%=43.75%.
(3)图中还提供了其他信息,例如该中学没有获得满分的同学,请再写出两条信息.
(3) 该中学参赛同学的成绩均不低于60 分;成绩在80 ~ 90 分(含80 分,但不含90 分)的人数最多. (答案不唯一,合理即可)
新课讲解
例
4. 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100根麦穗,量得它们的长度(单位:cm)如下表所示.列出样本的频数分布表,画出频数分布直方图,并估计这种大麦穗长的分布情况.
解:在样本数据中,最大值是7.4,最小值是4.0,它们的差是7.4-4.0=3.4.
最大值与最小值的差是3.4,如果取组距为0.3,那么由于,所以可以分成12组,组数适合.于是取组距为0.3,组数为12.
计算最大值与最小值的差
决定组距与组数
新课讲解
画频数分布直方图.
从频数分布表和频数分布直方图看到,麦穗长度大部分落在5.2 cm至7.0 cm(不含7.0 cm)的范围,落在其他范围的较少.长度在5.8≤x<6.1范围的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6,4.6≤x<4.9, 7.0≤x<7.3,7.3≤x<7.6范围的麦穗根数很少,总共只有7根.由此可以估计这种大麦穗长主要分布在5.2 cm至7.0 cm (不含7.0 cm)的范围,其中穗长在5.8 cm至6.1 cm (不含6.1 cm)范围的大麦最多.
新课讲解
练一练
1. 如图反映了七年级(1)班全班同学从家到学校所需的平均时间,请根据直方图回答下列问题:
(1)七年级(1)班一共有多少名同学?
(2)从家到学校所需的平均时间在哪个范围
的同学最多?哪个范围的同学最少?
(3)你还能从图中获得什么信息?
解:(1)∵5+17+14+2+2=40(名),
∴七年级(1)班一共有40名同学.
(2)从家到学校所需的平均时间在10 min至20 min(不含20 min)的同学最多,30 min至40 min(不含40 min)的同学最少.
(3)超过75%的同学从家到学校所需的平均时间在10 min至30 min(不含30 min)的范围.(答案不唯一)
新课讲解
练一练
2. 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集的20株西红柿秧上小西红柿的个数如下:
将数据适当分组,绘制相应的频数
分布直方图,并分析这20株西红柿秧上小西红柿个数的分布情况.
解:在样本数据中,最大值是62,最小值是28,它们的差是62-28=34,当组距为8时,=4,可分为5组.
频数分布表如下:
频数分布直方图如图所示.
新课讲解
练一练
2. 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集的20株西红柿秧上小西红柿的个数如下:
将数据适当分组,绘制相应的频数
分布直方图,并分析这20株西红柿秧上小西红柿个数的分布情况.
从频数分布表、频数分布直方图看到,西红柿秧上
小西红柿的个数大部分落在36个到60个(不含60个)的
范围,共有5+7+4=16(株),落在其他范围的较少.其中小西红柿个数在44≤x<52范围的西红柿秧最多,有7株,而小西红柿个数在28≤x<36,60≤x<68范围的西红柿秧最少,均为2株.
新课讲解
知识点3 频数分布直方图的应用
例
5. 某社区为了解该社区居民为某地震灾区的捐款情况,对社区部分捐款户数进行分组统计(统计表如右表所示),数据整理成如图所示的不完整的统计图.
捐款分组统计表
组别 捐款额x/元
A 10≤x<100
B 100≤x<200
C 200≤x<300
D 300≤x<400
E x≥400
请结合图中相关数据回答下列问题:
(1) 本次调查的样本容量是多少?
(2) 求出 C 组的频数并补全频数分布直方图.
解:(1)根据题意,得本次调查的样本容量是 (210)÷(128%40%8%)12÷24%50.
20
14
4
(2)根据题意,得
C 组的频数是 50×40%=20;
D 组的频数是 50×28%=14;
E 组的频数是 50×8%=4.
补全的频数分布直方图如图所示.
新课讲解
例
158 158 160 168 159 159 151 158 159
168 158 164 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
6. 某校为了解七年级 630 名学生的身高情况,随机抽查了该校七年级 63 名学生的身高(单位:cm)如表:
请你估计该校七年级 630 名学生中身高不低于 164 cm 的人数.
解:(1) 确定所给数据的最大值和
最小值.
上述数据中最小值是 149,最大值是 172,它们的差是 17214923.
(2) 决定组距与组数.取组距为 3,
那么由于 ,
可分成 8 组,组数适合.
于是取组距为 3,组数为 8.
(3) 列频数分布表.
(4) 画频数分布直方图.
从图中可以看出该校七年级 630 名学生中身高不低于 164 cm 的人数约有 630×150(人).
新课讲解
运用统计表(图)解决问题的方法
解题时可采用数形结合法,注意频数分布直方图能显示各项的具体数量,而扇形统计图能显示各项所占的百分比的大小,且扇形统计图中所有扇形所占的百分比之和为 1,某项的具体数量除以其所占的百分比即可得到总体的数量.
技巧点拨
新课讲解
练一练
1. 某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾.下面是七年级各班一周收集的可回收垃圾的质量的频数表和如图
所示的频数分布直方图(每组含前一
个边界值,不含后一个边界值).
(1) 求 a 的值.
(2) 该年级这周收集的可回收垃圾被
回收后所得金额(0.8元/千克)能不能达到 50 元?
解:(1)由题中频数分布直方图可知,收集的可回收垃圾的质量在 4.5 kg~5.0 kg 范围内的频数 a4.
(2)∵ 该年级这周收集的可回收垃圾的质量小于 4.5×2+5×4+5.5×3+6=51.5(kg),
∴ 该年级这周收集的可回收垃圾被回收后所得金额小于 51.5×0.8=41.2(元),不能达到 50 元.
新课讲解
练一练
2. 国庆节前,某校开展以“我爱祖国”为主题的征文评比活动,作品的交稿时间为 11 月 1 日至 24 日,评委会把学生上交的作品篇数按 4 天一组分组统计,绘制成如图所示的频数分布直方图.
已知从左往右各小长方形的高的比为 2:3:4:6:4:1,第二组的频数为 18.
请回答下列问题:
(1) 本次活动共有多少篇作品参加评比?
(2) 哪组上交的作品数量最多?是多少?
(3) 经过评比,第四组和第六组分别有 20 篇、4 篇作品获奖,则这两组哪组的获奖率高?
解:(1)∵从左往右各小长方形的高的比为 2:3:4:6:4:1,
∴从左往右各组的频数的比为 2:3:4:6:4:1.
∵第二组的频数为18,
∴总数为(篇).
∴本次活动共有120篇作品参加评比.
(2)第四组上交的作品数量最多,为 (篇).
(3)第六组上交的作品数量为 (篇).
第四组的获奖率为 2036100%56%,
第六组的获奖率为 46100%67%.
∵ 56%67%,∴ 第六组的获奖率高.
课堂小结
特点
能够显示一组连续数据的分布情况
计算最大值与最小值的差
决定组距和组数
列频数分布表
绘制频数分布直方图
直方图
绘制步骤
频数
落在各个小组内的数据的个数
当堂小练
1. 某市视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数分布直方图,则这组数据的组数与组距分别是( )
A. 4 和 0.20
B. 4 和 0.30
C. 5 和 0.20
D. 5 和 0.30
D
组距:4.253.95=0.30
当堂小练
2. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图如图所示,由图可知,下列结论正确的是( )
A. 最喜欢篮球的人数最多
B. 最喜欢羽毛球的人数是最喜欢乒乓球
人数的两倍
C. 全班共有 50 名学生
D. 最喜欢田径的人数占总人数的 10%
足球
12+20+8+4+6=50(名)
4÷50×100%=8%
C
6
8
当堂小练
3. 一个容量为 80 的样本,最大值为 143,最小值为 50,取组距为 10,则可以分成( )
A. 10 组 B. 9 组
C. 8 组 D. 7 组
A
组数:9+1=10
4. 一个样本有100个数据,最大值为7.4,最小值为4.0,如果取组距为0.3,那么这组数据可分成( )
A.11组 B.12组 C.13组 D.以上答案均不对
B
当堂小练
6. 在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
7. 如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
B
C
当堂小练
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
解:(1)a=50-4-8-16-10=12.
(2)如图.
7. 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出频数分布表和频数直方图(不完整)如下:
当堂小练
8. 某市教育局在全市党员教职工中开展“学习新党章、树立新形象”的活动,并进行了论文的评比,论文的交稿时间为 11 月 1 日至 24 日,评委会把各校上交的论文篇数按 4 天一组进行分组统计,绘制成如图所示的频数分布直方图(每组包括左端点,不包括右端点). 已知从左往右各小长方形的高的比为 2∶3∶4∶6∶4∶1,
第二组的频数为 18. 请回答下列问题:
解 :(1)因为从左往右各小长方形的高的比为 2∶ 3∶ 4∶6∶ 4∶ 1,所以从左往右各组的频数的比为 2∶ 3∶ 4∶ 6∶ 4∶ 1.因为第二组的频数为 18,所以本次活动共有 18÷=120(篇)论文参加评比 .
(1)本次活动共有多少篇论文参加评比?
(2)哪组上交的论文篇数最多?是多少?
(3)经过评比,第四组和第六组分别有 20 篇、4 篇论文获奖,则这两组哪组的获奖率高?
(2)观察频数分布直方图可知,第四组的小长方形最高,所以该组的频数最大,所以第四组上交的论文篇数最多,是× 120 =36(篇).
(3)第四组的获奖率为20÷36×100%≈56%,第六组的获奖率为4÷(120×) ×100% ≈ 67%.因为 56%<67%, 所以第六组的获奖率高 .
当堂小练
9. 为了加强对青少年防溺水安全教育,某学校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.从全校随机抽取了50名学生的竞赛成绩进行整理、描述和分析,比赛成绩用x表示,共分为五个等级:A:50≤x<60;B:60≤x<70;C:70≤x<80;D:80≤x<90;E:90≤x≤100. 并根据结果绘制成如下两幅不完整的频数分布直方图和扇形图.
(1)补全频数分布直方图.
(2)扇形统计图中比赛成绩为E等级和D等级所在扇形的圆心角的度数之和是多少?
(3)竞赛成绩90分及以上的同学会被评为“安全标兵”,请估计全校参加比赛的1800名学生中获此殊荣的人数.
解:(1)比赛成绩为B等级的学生为50×24%=12(人).补全频数分布直方图如图.
(2)扇形图中比赛成绩为E等级和D等级所在扇形的圆心角的度数之和是360× +360×20%=129.6.
(3)在样本中,比赛成绩90分及以上的同学所占的百分比为×100%=16%,
所以估计全校参加比赛的1800名学生中被评为“安全标兵”的有1800×36%=288(人).
当堂小练
10. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区 450 户居民的生活用水情况.他从中随机调查了若干户居民的月均用水量 x(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1) 频数分布表中,a______,b ______,c_____.
15
30%
6
a502121063215
b=15÷50×100%=30%
c5012%6
调查总户数:2÷4%=50
(2) 补全频数分布直方图.
15
6
(3) 如果家庭月均用水量“大于或等于 4 t 且小于 7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
解:由题意得,总体中中等用水量家庭大约有 450×(30%+20%+12%)=279(户).
对接中考
1. 了解公园用地面积x(单位:公顷)的基本情况,某地随机调查了本地50个公园的用地面积,按照0<x≤4,4<x≤8,8<x≤12,12<x≤16,16<x≤20的分组绘制了如图所示的频数分布直方图,下列说法正确的是( )
A.a的值为20
B.用地面积在8<x≤12这一组的公园个数最多
C.用地面积在4<x≤8这一组的公园个数最少
D.这50个公园中有一半以上的公园用地面积超
过12公顷
B
对接中考
2. 某校学生“亚运知识”竞赛成绩的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80分及以上的学生有 人.
140
对接中考
3. 为增强学生安全意识,某校举行了一次全校3000名学生参加的安全知识竞赛.从中随机抽取n名学生的竞赛成绩进行了分析,把成绩(满分100分,所有竞赛成绩均不低于60分)分成四个等级(D:60≤x<70;C:70≤x<80;B:80≤x<90;A:90≤x≤100),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.请根据以上信息,解答下列问题:
(1) 填空:n= ,m= ;
(2) 请补全频数分布直方图;
(3) 扇形统计图中B等级所在扇形的圆心角度数为 度;
(4) 若把A等级定为“优秀”等级,请你估计该校参加竞赛的3000名学生中达到“优秀”等级的学生人数.
150
36
D等级学生有:150﹣54﹣60﹣24=12(人).
12
144
∵3000×16%=480(人),
∴该校参加竞赛的3000名学生中达到“优秀”等级的学生人数约为480人.
第十二章 数据的收集、整理与描述
12.2 用统计图描述数据
12.2.2 直方图
目
录
1. 学习目标
4. 知识点1 频数分布表
7. 课堂小结
8. 当堂小练
CONTENTS
2. 知识回顾
5. 知识点2 频数分布直方图
9. 对接中考
3. 新课导入
6. 知识点3 频数分布直方图的应用
1.理解频数分布直方图及其相关概念;会制作频数分布表;会画频数分布直方图.
2.能利用直方图描述数据,能够从直方图中获取相关信息,培养数据分析能力,并解决实际问题.
学习目标
知识回顾
我们已经学习了哪些描述数据的方法?
扇形统计图
条形统计图
折线统计图
新课导入
我们已经学习过了条形图、折线图、扇形图等描述数据的方法,本节我们将学习另一种常用来描述数据的统计图——直方图.
新课讲解
知识点1 频数分布表
【问题1】为了举办运动会,学校准备从七年级学生中挑选身高接近的40人组成入场式仪仗队.有63人报名参加选拔,他们的身高(单位:cm)数据如下表所示.
选择身高在哪个范围的学生可以使仪仗队看起来比较整齐?
1. 计算最大值与最小值的差
在下表的数据中,最大值是172,最小值是149,最大值与最小值的差是23,说明身高的变化范围是23.
新课讲解
2. 决定组距和组数
把所有数据分成若干组,每个小组的两个端点间的距离 (组内数据的取值范围)称为组距.根据问题的需要,各组的组距可以相同或不同.
在本问题中, 我们作等距分组,即令各组的组距相同.
②数据分组:(x表示身高值)
149≤x<152,
152≤x<155,
…,
170≤x<173.
①组距与组数
组距为3
组数为8
当数据在100个以内时,按照数据的多少,常分成5~12组.
新课讲解
3. 列频数分布表
对落在各个小组内的数据进行累计,得到各个小组内的数据的个数叫作频数.整理可得下面的频数分布表:
新课讲解
1. 各小组的频数之和等于总数;
2. 组距可以相同,也可以不同;为研究方便,本节中我们作等距分组;
3. 数据所分组数没有明确要求,当数据在100 个以内时,根据数据的多少,常分成5 ~ 12 组.
数据分组时,可以先确定组距,再根据组距确定组数;也可以先确定组数,再根据组数确定组距 .
注意
新课讲解
频数分布表制作步骤
1. 算:计算最大值与最小值的差,得到数据的变化范围.
2. 定:根据数据的个数与数据的变化范围,确定组距、组数.
3. 划:利用划记的方法累计落在各组内的数据个数,得到各组的频数.
4. 列:根据上述过程列频数分布表. 频数分布表一般由数据分组、划记、频数三部分组成.
归纳
新课讲解
例
1. 有60 个数据,其中最大的数据是187,最小的数据是140,如果分组时的组距为6,那么这组数据应分为( )
A. 7 组 B. 7 组 C. 8 组 D. 10 组
解:因为 =7,所以这组数据应分为8 组.
C
新课讲解
例
2. 七年级某班20 名男生某次投掷标枪的测试成绩如下(单位:m):25,21,23,25,27,29,25,28,28,29,26,24,25,27,26,22,24,25,26,28.
(1) 将这20 名男生的测试成绩按从小到大的顺序排列,统计出每种成绩的数值出现的频数,并制成频数分布表.
解:(1)这20 名男生的测试成绩按从小到大的顺序排列如下( 单位:m):
21,22,23,24,24,25,25,25,25,25,26,26,26,27,27,28,28,28,29,29.
频数分布表如下:
测试成绩(单位:m) 21 22 23 24 25 26 27 28 29
划记
频数 1 1 1 2 5 3 2 3 2
(2) 根据频数分布表回答:
①成绩小于25 m 的男生有几人?占总人数的百分之几?
②成绩大于27 m 的男生有几人?占总人数的百分之几?
(2)由频数分布表可知:①成绩小于25 m 的男生有5 人,占总人数的25%.
②成绩大于27 m 的男生有5 人,占总人数的25%.
新课讲解
练一练
1. 已知样本 21,21,22,23,24,25,25,25,26,26,26,27,28,29,29,30. 若组距为 2,那么组数是____________.
5
新课讲解
练一练
2. 某校学生会为了了解全校学生对艺体项目的喜爱情况,随机调查了200 名学生(每名学生仅选一项最喜爱的项目),根据调查结果制作了如下频数分布表:
最喜爱的项目 频数 百分比
篮球 28%
排球 24 12%
乒乓球 48 24%
健美操
武术操 22 11%
跑步 20 10%
合计 200 1
(1)补全频数分布表.
56
30
15%
(2)在这次抽样调查中,最喜爱哪个项目的学生最多?最喜爱哪个项目的学生最少?
解:(2) 最喜爱篮球的学生最多,最喜爱跑步的学生最少.
(3)根据以上调查,试估计该校1620 名学生中最喜爱健美操的有多少名.
(3) 估计该校1620名学生中最喜爱健美操的有1620×15%=243(名).
新课讲解
知识点2 频数分布直方图
4. 画频数分布直方图
频数分布直方图是以小长方形的面积来反映数据落在各个小组内的频数的大小,小长方形的高是频数与组距的比值.
为了更直观形象地看出频数分布的情况,可以根据频数分布表画出频数分布直方图.
画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
小长方形的宽是组距
小长方形的高是频数与组距的比值
横轴
纵轴
新课讲解
从频数分布表和频数分布直方图中可以看出,身高在155≤x<158,158≤x<161, 161≤x<164三个组的人数最多,共有12+19+10=41(人).因此,可以从身高在155 cm至164 cm(不含164 cm)范围的同学中挑选仪仗队队员.
新课讲解
画频数分布直方图的基本步骤
1. 算:计算最大值与最小值的差,确定数据值的变化范围.
2. 定:决定组距和组数,当数据在100个以内时,按照数据的多少,常分成5~12组.
3. 列:列频数分布表.
4. 画:画频数分布直方图.
归纳
新课讲解
画等距分组的频数分布直方图时,为画图与看图方便,通常直接用小长方形的高表示频数.
1. 直方图中的各小长方形之间没有空隙;
2. 一般情况下,相邻各分点的归宿:“上限不在内”.
新课讲解
等距分组的频数分布直方图的画法.
1. 画两条互相垂直的轴:横轴和纵轴;
2. 在横轴上划分一些相互衔接的线段,每条线段表示一组,在每条线段的左端点标明这组的下限,在线段的右端点标明其上限;
3. 在纵轴上划分刻度,并用自然数标记;
4. 以横轴上的每条线段为底各作一个长方形立于横轴上,使各长方形的高等于相应的频数.
新课讲解
直方图与条形图的区别
条形图 直方图
用小长方形的高度表示数据的大小 以小长方形的面积来表示频数的大小
横轴上的数据是孤立的,相邻的数据没有联系 横轴上相邻的数据有必然联系,它表示一个范围
各个小长方形之间有间隔 相邻的小长方形之间没有间隔
侧重反映每个项目具体数目的多少 描述的是一组连续的数据,它侧重反映这些数据落在各小组内的频数的分布情况
新课讲解
例
3. 某中学部分同学参加数学竞赛,取得了优异的成绩,指导老师统计了所有参赛同学的成绩(成绩都是整数,试题满分为120 分),
并且绘制了如图所示的频数分布直方图(每组中含
最低分数,但不含最高分数),请回答:
(1)该中学参加本次数学竞赛的共有多少人?
(2)如果成绩在90分以上(含90 分)的同学获奖,那么该中学参赛同学的获奖率是多少?
解:由频数分布直方图知,从左到右各分数段的人数分别为4,6,8,7,5,2.
(1) 4+6+8+7+5+2=32(人). 所以该中学参加本次数学竞赛的共有32 人.
(2) 成绩在90 分以上(含90 分)的同学有7+5+2=14(人),
所以该中学参赛同学的获奖率是 ×100%=43.75%.
(3)图中还提供了其他信息,例如该中学没有获得满分的同学,请再写出两条信息.
(3) 该中学参赛同学的成绩均不低于60 分;成绩在80 ~ 90 分(含80 分,但不含90 分)的人数最多. (答案不唯一,合理即可)
新课讲解
例
4. 为了考察某种大麦穗长的分布情况,在一块试验田里抽取了100根麦穗,量得它们的长度(单位:cm)如下表所示.列出样本的频数分布表,画出频数分布直方图,并估计这种大麦穗长的分布情况.
解:在样本数据中,最大值是7.4,最小值是4.0,它们的差是7.4-4.0=3.4.
最大值与最小值的差是3.4,如果取组距为0.3,那么由于,所以可以分成12组,组数适合.于是取组距为0.3,组数为12.
计算最大值与最小值的差
决定组距与组数
新课讲解
画频数分布直方图.
从频数分布表和频数分布直方图看到,麦穗长度大部分落在5.2 cm至7.0 cm(不含7.0 cm)的范围,落在其他范围的较少.长度在5.8≤x<6.1范围的麦穗根数最多,有28根,而长度在4.0≤x<4.3,4.3≤x<4.6,4.6≤x<4.9, 7.0≤x<7.3,7.3≤x<7.6范围的麦穗根数很少,总共只有7根.由此可以估计这种大麦穗长主要分布在5.2 cm至7.0 cm (不含7.0 cm)的范围,其中穗长在5.8 cm至6.1 cm (不含6.1 cm)范围的大麦最多.
新课讲解
练一练
1. 如图反映了七年级(1)班全班同学从家到学校所需的平均时间,请根据直方图回答下列问题:
(1)七年级(1)班一共有多少名同学?
(2)从家到学校所需的平均时间在哪个范围
的同学最多?哪个范围的同学最少?
(3)你还能从图中获得什么信息?
解:(1)∵5+17+14+2+2=40(名),
∴七年级(1)班一共有40名同学.
(2)从家到学校所需的平均时间在10 min至20 min(不含20 min)的同学最多,30 min至40 min(不含40 min)的同学最少.
(3)超过75%的同学从家到学校所需的平均时间在10 min至30 min(不含30 min)的范围.(答案不唯一)
新课讲解
练一练
2. 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集的20株西红柿秧上小西红柿的个数如下:
将数据适当分组,绘制相应的频数
分布直方图,并分析这20株西红柿秧上小西红柿个数的分布情况.
解:在样本数据中,最大值是62,最小值是28,它们的差是62-28=34,当组距为8时,=4,可分为5组.
频数分布表如下:
频数分布直方图如图所示.
新课讲解
练一练
2. 阳泉同学参加周末社会实践活动,到“富乐花乡”蔬菜大棚中收集的20株西红柿秧上小西红柿的个数如下:
将数据适当分组,绘制相应的频数
分布直方图,并分析这20株西红柿秧上小西红柿个数的分布情况.
从频数分布表、频数分布直方图看到,西红柿秧上
小西红柿的个数大部分落在36个到60个(不含60个)的
范围,共有5+7+4=16(株),落在其他范围的较少.其中小西红柿个数在44≤x<52范围的西红柿秧最多,有7株,而小西红柿个数在28≤x<36,60≤x<68范围的西红柿秧最少,均为2株.
新课讲解
知识点3 频数分布直方图的应用
例
5. 某社区为了解该社区居民为某地震灾区的捐款情况,对社区部分捐款户数进行分组统计(统计表如右表所示),数据整理成如图所示的不完整的统计图.
捐款分组统计表
组别 捐款额x/元
A 10≤x<100
B 100≤x<200
C 200≤x<300
D 300≤x<400
E x≥400
请结合图中相关数据回答下列问题:
(1) 本次调查的样本容量是多少?
(2) 求出 C 组的频数并补全频数分布直方图.
解:(1)根据题意,得本次调查的样本容量是 (210)÷(128%40%8%)12÷24%50.
20
14
4
(2)根据题意,得
C 组的频数是 50×40%=20;
D 组的频数是 50×28%=14;
E 组的频数是 50×8%=4.
补全的频数分布直方图如图所示.
新课讲解
例
158 158 160 168 159 159 151 158 159
168 158 164 158 154 169 158 158 158
159 167 170 153 160 160 159 159 160
149 163 163 162 172 161 153 156 162
162 163 157 162 162 161 157 157 164
155 156 165 166 156 154 166 164 165
156 157 153 165 159 157 155 164 156
6. 某校为了解七年级 630 名学生的身高情况,随机抽查了该校七年级 63 名学生的身高(单位:cm)如表:
请你估计该校七年级 630 名学生中身高不低于 164 cm 的人数.
解:(1) 确定所给数据的最大值和
最小值.
上述数据中最小值是 149,最大值是 172,它们的差是 17214923.
(2) 决定组距与组数.取组距为 3,
那么由于 ,
可分成 8 组,组数适合.
于是取组距为 3,组数为 8.
(3) 列频数分布表.
(4) 画频数分布直方图.
从图中可以看出该校七年级 630 名学生中身高不低于 164 cm 的人数约有 630×150(人).
新课讲解
运用统计表(图)解决问题的方法
解题时可采用数形结合法,注意频数分布直方图能显示各项的具体数量,而扇形统计图能显示各项所占的百分比的大小,且扇形统计图中所有扇形所占的百分比之和为 1,某项的具体数量除以其所占的百分比即可得到总体的数量.
技巧点拨
新课讲解
练一练
1. 某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾.下面是七年级各班一周收集的可回收垃圾的质量的频数表和如图
所示的频数分布直方图(每组含前一
个边界值,不含后一个边界值).
(1) 求 a 的值.
(2) 该年级这周收集的可回收垃圾被
回收后所得金额(0.8元/千克)能不能达到 50 元?
解:(1)由题中频数分布直方图可知,收集的可回收垃圾的质量在 4.5 kg~5.0 kg 范围内的频数 a4.
(2)∵ 该年级这周收集的可回收垃圾的质量小于 4.5×2+5×4+5.5×3+6=51.5(kg),
∴ 该年级这周收集的可回收垃圾被回收后所得金额小于 51.5×0.8=41.2(元),不能达到 50 元.
新课讲解
练一练
2. 国庆节前,某校开展以“我爱祖国”为主题的征文评比活动,作品的交稿时间为 11 月 1 日至 24 日,评委会把学生上交的作品篇数按 4 天一组分组统计,绘制成如图所示的频数分布直方图.
已知从左往右各小长方形的高的比为 2:3:4:6:4:1,第二组的频数为 18.
请回答下列问题:
(1) 本次活动共有多少篇作品参加评比?
(2) 哪组上交的作品数量最多?是多少?
(3) 经过评比,第四组和第六组分别有 20 篇、4 篇作品获奖,则这两组哪组的获奖率高?
解:(1)∵从左往右各小长方形的高的比为 2:3:4:6:4:1,
∴从左往右各组的频数的比为 2:3:4:6:4:1.
∵第二组的频数为18,
∴总数为(篇).
∴本次活动共有120篇作品参加评比.
(2)第四组上交的作品数量最多,为 (篇).
(3)第六组上交的作品数量为 (篇).
第四组的获奖率为 2036100%56%,
第六组的获奖率为 46100%67%.
∵ 56%67%,∴ 第六组的获奖率高.
课堂小结
特点
能够显示一组连续数据的分布情况
计算最大值与最小值的差
决定组距和组数
列频数分布表
绘制频数分布直方图
直方图
绘制步骤
频数
落在各个小组内的数据的个数
当堂小练
1. 某市视力健康管理中心对全市初中生的视力情况进行了一次抽样调查,如图是利用调查所得数据绘制的频数分布直方图,则这组数据的组数与组距分别是( )
A. 4 和 0.20
B. 4 和 0.30
C. 5 和 0.20
D. 5 和 0.30
D
组距:4.253.95=0.30
当堂小练
2. 某班组织了针对全班同学关于“你最喜欢的一项体育活动”的问卷调查后,绘制出频数分布直方图如图所示,由图可知,下列结论正确的是( )
A. 最喜欢篮球的人数最多
B. 最喜欢羽毛球的人数是最喜欢乒乓球
人数的两倍
C. 全班共有 50 名学生
D. 最喜欢田径的人数占总人数的 10%
足球
12+20+8+4+6=50(名)
4÷50×100%=8%
C
6
8
当堂小练
3. 一个容量为 80 的样本,最大值为 143,最小值为 50,取组距为 10,则可以分成( )
A. 10 组 B. 9 组
C. 8 组 D. 7 组
A
组数:9+1=10
4. 一个样本有100个数据,最大值为7.4,最小值为4.0,如果取组距为0.3,那么这组数据可分成( )
A.11组 B.12组 C.13组 D.以上答案均不对
B
当堂小练
6. 在频数分布表中,各小组的频数之和( )
A.小于数据总数 B.等于数据总数
C.大于数据总数 D.不能确定
7. 如图是某班45名同学爱心捐款额的频数直方图(每组含前一个边界值,不含后一个边界值),则捐款人数最多的一组是( )
A.5~10元 B.10~15元
C.15~20元 D.20~25元
B
C
当堂小练
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?
解:(1)a=50-4-8-16-10=12.
(2)如图.
7. 为了提高学生书写汉字的能力,增强保护汉字的意识,我市举办了首届“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出频数分布表和频数直方图(不完整)如下:
当堂小练
8. 某市教育局在全市党员教职工中开展“学习新党章、树立新形象”的活动,并进行了论文的评比,论文的交稿时间为 11 月 1 日至 24 日,评委会把各校上交的论文篇数按 4 天一组进行分组统计,绘制成如图所示的频数分布直方图(每组包括左端点,不包括右端点). 已知从左往右各小长方形的高的比为 2∶3∶4∶6∶4∶1,
第二组的频数为 18. 请回答下列问题:
解 :(1)因为从左往右各小长方形的高的比为 2∶ 3∶ 4∶6∶ 4∶ 1,所以从左往右各组的频数的比为 2∶ 3∶ 4∶ 6∶ 4∶ 1.因为第二组的频数为 18,所以本次活动共有 18÷=120(篇)论文参加评比 .
(1)本次活动共有多少篇论文参加评比?
(2)哪组上交的论文篇数最多?是多少?
(3)经过评比,第四组和第六组分别有 20 篇、4 篇论文获奖,则这两组哪组的获奖率高?
(2)观察频数分布直方图可知,第四组的小长方形最高,所以该组的频数最大,所以第四组上交的论文篇数最多,是× 120 =36(篇).
(3)第四组的获奖率为20÷36×100%≈56%,第六组的获奖率为4÷(120×) ×100% ≈ 67%.因为 56%<67%, 所以第六组的获奖率高 .
当堂小练
9. 为了加强对青少年防溺水安全教育,某学校开展了“远离溺水,珍爱生命”的防溺水安全知识比赛.从全校随机抽取了50名学生的竞赛成绩进行整理、描述和分析,比赛成绩用x表示,共分为五个等级:A:50≤x<60;B:60≤x<70;C:70≤x<80;D:80≤x<90;E:90≤x≤100. 并根据结果绘制成如下两幅不完整的频数分布直方图和扇形图.
(1)补全频数分布直方图.
(2)扇形统计图中比赛成绩为E等级和D等级所在扇形的圆心角的度数之和是多少?
(3)竞赛成绩90分及以上的同学会被评为“安全标兵”,请估计全校参加比赛的1800名学生中获此殊荣的人数.
解:(1)比赛成绩为B等级的学生为50×24%=12(人).补全频数分布直方图如图.
(2)扇形图中比赛成绩为E等级和D等级所在扇形的圆心角的度数之和是360× +360×20%=129.6.
(3)在样本中,比赛成绩90分及以上的同学所占的百分比为×100%=16%,
所以估计全校参加比赛的1800名学生中被评为“安全标兵”的有1800×36%=288(人).
当堂小练
10. 小军同学在学校组织的社会调查活动中负责了解他所居住的小区 450 户居民的生活用水情况.他从中随机调查了若干户居民的月均用水量 x(单位:t),并绘制了样本的频数分布表和频数分布直方图(如图).
(1) 频数分布表中,a______,b ______,c_____.
15
30%
6
a502121063215
b=15÷50×100%=30%
c5012%6
调查总户数:2÷4%=50
(2) 补全频数分布直方图.
15
6
(3) 如果家庭月均用水量“大于或等于 4 t 且小于 7 t”为中等用水量家庭,请你通过样本估计总体中的中等用水量家庭大约有多少户.
解:由题意得,总体中中等用水量家庭大约有 450×(30%+20%+12%)=279(户).
对接中考
1. 了解公园用地面积x(单位:公顷)的基本情况,某地随机调查了本地50个公园的用地面积,按照0<x≤4,4<x≤8,8<x≤12,12<x≤16,16<x≤20的分组绘制了如图所示的频数分布直方图,下列说法正确的是( )
A.a的值为20
B.用地面积在8<x≤12这一组的公园个数最多
C.用地面积在4<x≤8这一组的公园个数最少
D.这50个公园中有一半以上的公园用地面积超
过12公顷
B
对接中考
2. 某校学生“亚运知识”竞赛成绩的频数分布直方图(每一组含前一个边界值,不含后一个边界值)如图所示,其中成绩在80分及以上的学生有 人.
140
对接中考
3. 为增强学生安全意识,某校举行了一次全校3000名学生参加的安全知识竞赛.从中随机抽取n名学生的竞赛成绩进行了分析,把成绩(满分100分,所有竞赛成绩均不低于60分)分成四个等级(D:60≤x<70;C:70≤x<80;B:80≤x<90;A:90≤x≤100),并根据分析结果绘制了不完整的频数分布直方图和扇形统计图.请根据以上信息,解答下列问题:
(1) 填空:n= ,m= ;
(2) 请补全频数分布直方图;
(3) 扇形统计图中B等级所在扇形的圆心角度数为 度;
(4) 若把A等级定为“优秀”等级,请你估计该校参加竞赛的3000名学生中达到“优秀”等级的学生人数.
150
36
D等级学生有:150﹣54﹣60﹣24=12(人).
12
144
∵3000×16%=480(人),
∴该校参加竞赛的3000名学生中达到“优秀”等级的学生人数约为480人.
同课章节目录
