期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 14:50:19 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2024春 福建期末)已知非零向量,满足,且向量在向量上的投影向量是,则与的夹角是( )
A. B. C. D.
2.(2025春 滨湖区校级期末)已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A与B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
3.(2024春 武威期末)复数的虚部为( )
A. B. C.1 D.2
4.(2023春 河北期末)元宵节是春节之后的第一个重要节日,元宵节又称灯节,很多地区家家户户都挂花灯.下图是小明为自家设计的一个花灯,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为40cm和20cm,正六棱台与正六棱柱的高分别为10cm和60cm,则该花灯的体积为( )
A. B.
C. D.
5.(2024春 大通县期末)用2,3,4这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”发生的概率为( )
A. B. C. D.
6.(2024春 丽江期末)在平行四边形ABCD中(1,0),(2,1),则( )
A.4 B.﹣4 C.1 D.﹣1
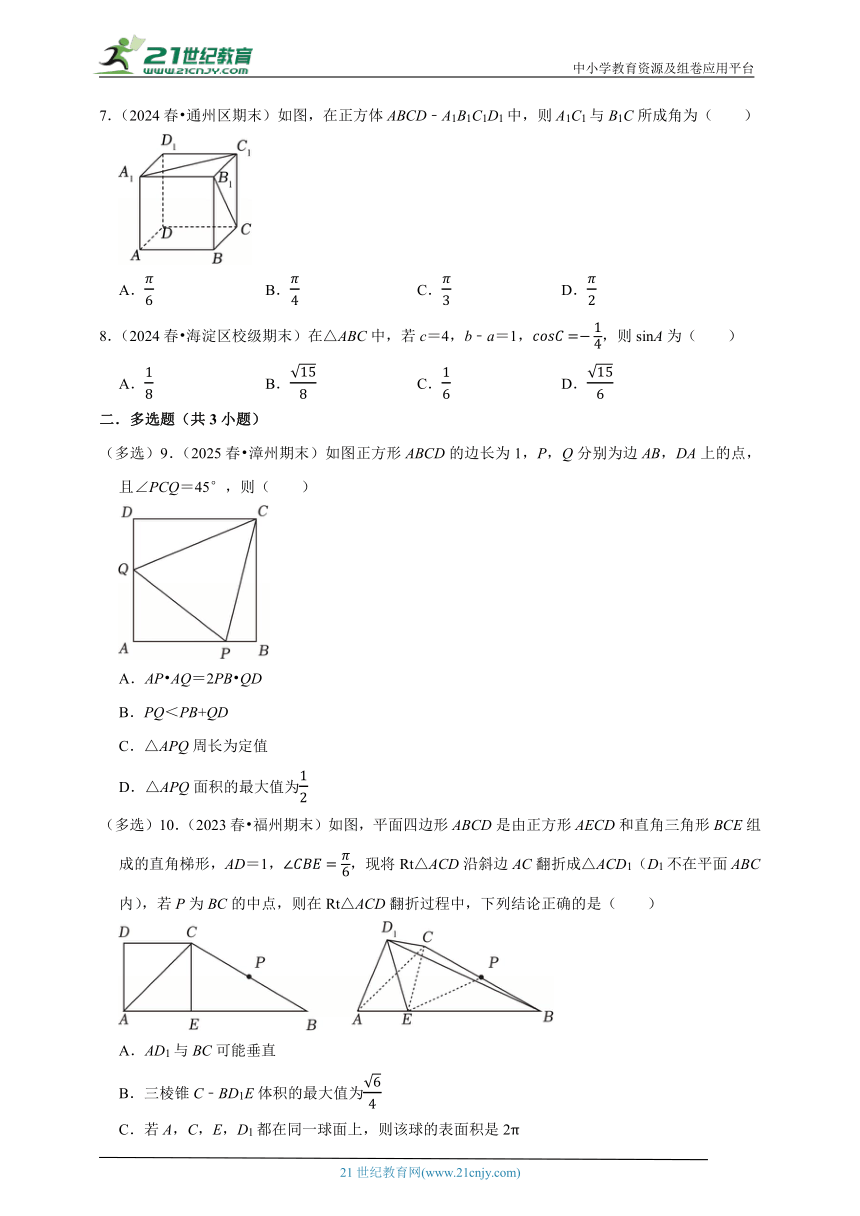
7.(2024春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,则A1C1与B1C所成角为( )
A. B. C. D.
8.(2024春 海淀区校级期末)在△ABC中,若c=4,b﹣a=1,,则sinA为( )
A. B. C. D.
二.多选题(共3小题)
(多选)9.(2025春 漳州期末)如图正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且∠PCQ=45°,则( )
A.AP AQ=2PB QD
B.PQ<PB+QD
C.△APQ周长为定值
D.△APQ面积的最大值为
(多选)10.(2023春 福州期末)如图,平面四边形ABCD是由正方形AECD和直角三角形BCE组成的直角梯形,AD=1,,现将Rt△ACD沿斜边AC翻折成△ACD1(D1不在平面ABC内),若P为BC的中点,则在Rt△ACD翻折过程中,下列结论正确的是( )
A.AD1与BC可能垂直
B.三棱锥C﹣BD1E体积的最大值为
C.若A,C,E,D1都在同一球面上,则该球的表面积是2π
D.直线AD1与EP所成角的取值范围为
(多选)11.(2025春 海曙区校级期末)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O为正方体的中心,M为DD1的中点,F为侧面正方形AA1D1D内一动点,且满足B1F∥平面BC1M,则( )
A.三棱锥D1﹣DCB的外接球表面积为12π
B.动点F的轨迹是一条线段
C.三棱锥F﹣BC1M的体积是随点F的运动而变化的
D.若过A,M,C1三点作正方体的截面Ω,Q为截面Ω上一点,则线段A1Q长度的取值范围为
三.填空题(共3小题)
12.(2025春 静安区期末)连续抛掷一枚质地均匀的硬币4次,并记录朝上的一面是正面还是反面,则恰好出现正面与反面朝上都是2次的概率是 .
13.(2025春 宝山区期末)如图,以边长为1的正方形ABCD的各边为基准向外作正三角形,构成八边形AFBGCHDE.若点P、Q在八边形的内部(含边界),则的最小值为 .
14.(2024秋 宝山区校级期末)如图,已知直四棱柱ABCD﹣A1B1C1D1的所有棱长等于1,∠ABC=120°,O和O1分别是上下底面对角线的交点,H在线段OB1上,OH=3HB1,点M在线段BD上移动,则三棱锥M﹣C1O1H的体积最小值为 .
四.解答题(共5小题)
15.(2024春 锡林郭勒盟期末)已知向量,,
(Ⅰ)若,求实数x的值;
(Ⅱ)若,求向量与的夹角的余弦值.
16.(2023春 湘潭县期末)在△ABC中,设角A,B,C的对边长分别为a,b,c.
(1)若,,,求△ABC的周长;
(2)若点D是BC边上一点,且CD=2,BD=1,b2+2c2=9,求AD的长.
17.(2024秋 宁城县期末)某中学为研究本校高三学生在市联考中的语文成绩,随机抽取了100位同学的语文成绩作为样本,得到以[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组的样本频率分布直方图如图.
(1)求直方图中x的值;
(2)请估计本次联考该校语文成绩的中位数和平均数;
(3)样本内语文分数在[130,140),[140,150]的两组学生中,用分层抽样的方法抽取5名学生,再从这5名学生中随机选出2人,求选出的两名学生中恰有一人成绩在[130,140)中的概率.
18.(2024春 东坡区期末)在①,②,③sin2A﹣cos2B+cos2C=sinAsinB这三个条件中任选一个,补充在下面问题中,并完成解答.
在△ABC中,角A、B、C的对边分别为a、b、c,已知_____.
(1)求角C;
(2)若c=1,△ABC的面积,求△ABC的周长l的取值范围;
(3)若,,求tan∠ABD.
注:如果选择多个条件分别解答,按第一个解答计分.
19.(2024春 达拉特旗校级期末)如图,在直三棱柱ABC﹣A1B1C1中,,AB=2AC=4,AC⊥CB,点D,E分别为棱BC,A1C1的中点,点F是线段CE的中点.
(1)求证:AF⊥平面BCE;
(2)求直线DF与平面ABF所成角的正弦值;
(3)求二面角F﹣AD﹣C的余弦值.
期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A B B C C C C B
二.多选题(共3小题)
题号 9 10 11
答案 AC ACD ABD
一.选择题(共8小题)
1.(2024春 福建期末)已知非零向量,满足,且向量在向量上的投影向量是,则与的夹角是( )
A. B. C. D.
【解答】解:因为,
所以,
所以,
因为向量在向量上的投影向量是,
所以,
即,所以,
又因为,
所以与的夹角是.
故选:A.
2.(2025春 滨湖区校级期末)已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A与B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
【解答】解:已知事件A,B满足P(A)=0.5,P(B)=0.2,
选项A:若B A,则P(AB)=P(B)=0.2,
选项B:若A与B互斥,则P(A+B)=0.7=P(A)+P(B).故选项B正确.
选项C:若A与B相互独立,则 A与相互独立,,故选项C错误.
选项D:若P(B)+P(C)=1,则由于不确定C与B是否互斥,所以无法确定两事件是否对立,故D错误.
故选:B.
3.(2024春 武威期末)复数的虚部为( )
A. B. C.1 D.2
【解答】解:,
则复数的虚部为.
故选:B.
4.(2023春 河北期末)元宵节是春节之后的第一个重要节日,元宵节又称灯节,很多地区家家户户都挂花灯.下图是小明为自家设计的一个花灯,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为40cm和20cm,正六棱台与正六棱柱的高分别为10cm和60cm,则该花灯的体积为( )
A. B.
C. D.
【解答】解:依题意,花灯的体积等于上面的正六棱台体积与下面的正六棱柱体积的和,
正六棱台的两个底面积分别为,,
所以花灯的体积.
故选:C.
5.(2024春 大通县期末)用2,3,4这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”发生的概率为( )
A. B. C. D.
【解答】解:将2,3,4组成一个没有重复数字的三位数的情况有{234,243,324,342,423,432},共6种,
其中偶数有{234,324,342,432},共4种,
所以事件“这个三位数是偶数”发生的概率为.
故选:C.
6.(2024春 丽江期末)在平行四边形ABCD中(1,0),(2,1),则( )
A.4 B.﹣4 C.1 D.﹣1
【解答】解:因为四边形ABCD为平行四边形,
所以,
所以.
故选:C.
7.(2024春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,则A1C1与B1C所成角为( )
A. B. C. D.
【解答】解:连接DA1,DC1,
在正方体ABCD﹣A1B1C1D1中,
A1B1∥CD且A1B1=CD,
即四边形A1B1CD是平行四边形,
所以DA1∥B1C,
所以∠DA1C1即为A1C1与B1C所成角.
又△DA1C1是等边三角形,
即∠DA1C1=60°,
所以A1C1与B1C所成的角为.
故选:C.
8.(2024春 海淀区校级期末)在△ABC中,若c=4,b﹣a=1,,则sinA为( )
A. B. C. D.
【解答】解:由余弦定理知,c2=a2+b2﹣2abcosC,
所以42=a2+(a+1)2﹣2a (a+1) (),整理得a2+a﹣6=0,
解得a=2或a=﹣3,
由,知sinC,
由正弦定理知,,
所以,
所以sinA.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 漳州期末)如图正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且∠PCQ=45°,则( )
A.AP AQ=2PB QD
B.PQ<PB+QD
C.△APQ周长为定值
D.△APQ面积的最大值为
【解答】解:在正方形ABCD中,延长AD到E,使DE=BP,连接CE,
由S△APQ+2(S△PBC+S△QDC)=1,得,
于是(1﹣PB)(1﹣QD)+2PB+2QD=2,整理得PB+QD+PB QD=1,
2PB QD=1﹣PB﹣QD+PB QD=(1﹣PB)(1﹣QD)=AP AQ,所以A正确;
由正方形的性质可得Rt△CDE≌Rt△CBP,
∠ECD=∠PCB,CE=CP,由∠PCQ=45°,
得∠ECQ=∠ECD+∠DCQ=∠BCP+∠DCQ=45°=∠PCQ,
于是△ECQ≌△PCQ,PQ=QE=PB+QD,所以B错误;
△APQ周长为AP+AQ+PQ=1﹣PB+1﹣QD+PQ=2,所以C正确;
由C选项分析,2=AP+AQ2
=(2),
即AP AQ≤()2=6﹣4,
当且仅当AP=AQ时取等号,,所以D错误.
故选:AC.
(多选)10.(2023春 福州期末)如图,平面四边形ABCD是由正方形AECD和直角三角形BCE组成的直角梯形,AD=1,,现将Rt△ACD沿斜边AC翻折成△ACD1(D1不在平面ABC内),若P为BC的中点,则在Rt△ACD翻折过程中,下列结论正确的是( )
A.AD1与BC可能垂直
B.三棱锥C﹣BD1E体积的最大值为
C.若A,C,E,D1都在同一球面上,则该球的表面积是2π
D.直线AD1与EP所成角的取值范围为
【解答】解:对于A,由AD⊥CD,则AD1⊥CD1,当AD1⊥D1B时,且D1B<AB,
此时满足AD1⊥平面BCD1,因此AD1⊥BC,选项A正确;
对于B,取AC的中点O,连接OE,OD1,
则,且OD1⊥AC,
因为,
当平面ACD1⊥平面ABC时,三棱锥C﹣BD1E体积的最大值,
在Rt△BCE中,∠CBE,CE=1,则,
此时,
所以三棱锥C﹣BD1E体积的最大值为,选项B错误;
对于C,因为,
所以A,C,E,D1都在同一球面上,且球的半径为,
所以该球的表面积是,选项C正确;
对于D,作AM∥EP,因为P为BC的中点,所以EP=1,
因为,所以,
所以∠BAM=∠ABC=30°,所以∠MAC=15°,
AD1可以看成以AC为轴线,且母线和底面所成角是45°的圆锥的母线,
所以AC与AD1夹角为45°,AC与AM夹角为15°,又D1不在平面ABC内,
且60°=45°+15°,30°=45°﹣15°,
所以AD1与DM所成角的取值范围是,所以选项D正确,
故选:ACD.
(多选)11.(2025春 海曙区校级期末)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O为正方体的中心,M为DD1的中点,F为侧面正方形AA1D1D内一动点,且满足B1F∥平面BC1M,则( )
A.三棱锥D1﹣DCB的外接球表面积为12π
B.动点F的轨迹是一条线段
C.三棱锥F﹣BC1M的体积是随点F的运动而变化的
D.若过A,M,C1三点作正方体的截面Ω,Q为截面Ω上一点,则线段A1Q长度的取值范围为
【解答】解:对于A,因为三棱锥D1﹣DCB的外接球与正方体ABCD﹣A1B1C1D1的外接球是同一个球,
因为正方体的外接球直径是正方体的体对角线,
设外接球半径为R,则2R=2,即R,
所以三棱锥D1﹣DCB的外接球表面积为4πR2=4π×3=12π,故A正确;
对于B,如图,分别取AA1,A1D1的中点H,G连接B1G,GH,HB1,AD1,
因为B1H∥C1M,B1H 平面BGH,C1M 平面BGH,
所以C1M∥平面BGH,
因为GH∥BC1,GH 平面BGH,BC1 平面BGH,
所以BC1∥平面BGH,
C1M 平面BC1M,BC1 平面BC1M,BC1∩C1M=C1,
所以平面B1GH∥平面BC1M,
而B1F∥平面BC1M,所以B1F 平面B1GH,所以点F轨迹为线段GH,故B正确;
由选项B可知,点F的轨迹为线段GH,因为GH∥平面BC1M,则点F到平面BC1M的距离为定值,
又△BC1M的面积为定值,从而可得三棱锥F﹣BC1M的体积是定值,故C不正确;
如图,设截面Ω与平面BAA1B1交于AN,N在BB1上,
因为截面Ω∩平面DAA1D1=AM,平面DAA1D1∥平面CBB1C1,
所以AM∥NC1,同理可证AN∥MC1,所以截面AMC1N为平行四边形,所以点N为BB1中点,
在四棱锥A1﹣AMC1N中,侧棱A1C1最长,且A1C1,设四棱锥A1﹣AMC1N的高为h,
因为AM=MC1,所以四边形AMC1N为菱形,
所以△AMC1的边AC1上的高为面对角线的一半,即为,又AC1,
则,,
所以,解得,
综上,可知线段A1Q长度的取值范围为,故D正确.
故选:ABD.
三.填空题(共3小题)
12.(2025春 静安区期末)连续抛掷一枚质地均匀的硬币4次,并记录朝上的一面是正面还是反面,则恰好出现正面与反面朝上都是2次的概率是 .
【解答】解:根据题意,连续抛掷一枚质地均匀的硬币4次,设正面向上的次数为X,则X=0、1、2、3、4,
易得X~B(4,),
若恰好出现正面与反面朝上都是2次,即X=2,则其概率P(X=2)()2(1)2.
故答案为:.
13.(2025春 宝山区期末)如图,以边长为1的正方形ABCD的各边为基准向外作正三角形,构成八边形AFBGCHDE.若点P、Q在八边形的内部(含边界),则的最小值为 .
【解答】解:由题意知, 的最小值为
||||cos∠FAH
=1cos135°
()
.
故答案为:.
14.(2024秋 宝山区校级期末)如图,已知直四棱柱ABCD﹣A1B1C1D1的所有棱长等于1,∠ABC=120°,O和O1分别是上下底面对角线的交点,H在线段OB1上,OH=3HB1,点M在线段BD上移动,则三棱锥M﹣C1O1H的体积最小值为 .
【解答】解:因为直四棱柱ABCD﹣A1B1C1D1的底面是菱形,∠ABC=120°,边长为1,
所以O1C1⊥平面BB1D1D,且,,
C1到平面BB1D1D的距离为,
因为OH=3HB1,点M是线段BD上的动点,
所以当△O1MH的面积取得最小值时,三棱锥C1﹣O1MH的体积有最小值.
将平面BB1D1D单独画图可得,
当M点到O1H的距离最小时,△O1MH的面积有最小值.
过点B作BF∥O1H,可得直线BF上方的点到O1H的距离比直线BF上的点到O1H的距离小,
而线段BD上除B点外的所有点都在直线BF下方,到O1H的距离比B点到O1H的距离大,
即当M点在B点时,△O1MH的面积取得最小值,且三棱锥C1﹣O1MH的体积有最小值.
连接O1B,则,
所以B1到O1B的距离,
因为OH=3HB1,
所以H到直线O1B的距离为,
所以,
所以.
故答案为:.
四.解答题(共5小题)
15.(2024春 锡林郭勒盟期末)已知向量,,
(Ⅰ)若,求实数x的值;
(Ⅱ)若,求向量与的夹角的余弦值.
【解答】解:(Ⅰ)已知向量,,
则,
又,
则(﹣4)×4=8(x﹣4),
即x=2;
(Ⅱ)由题意可得,
又,
则(﹣4)×(﹣2﹣x)+8×8=0,
即x=﹣18,
则,
则,
则向量与的夹角的余弦值为.
16.(2023春 湘潭县期末)在△ABC中,设角A,B,C的对边长分别为a,b,c.
(1)若,,,求△ABC的周长;
(2)若点D是BC边上一点,且CD=2,BD=1,b2+2c2=9,求AD的长.
【解答】解:(1)因为,,
所以.
由正弦定理,得,
所以.
(2)
设AD=x,在三角形ABD与三角形ACD中,由余弦定理得:
AB2=BD2+x2﹣2BD x cos∠ADB,AC2=CD2+x2﹣2CD x cos∠ADC,
所以12+x2﹣2x cos∠ADB=c2①,22+x2+4x cos∠ADB=b2②,
①×2+②得6+3x2=b2+2c2,
因为b2+2c2=9,所以6+3x2=9,解得x=1,
即AD的长为1.
17.(2024秋 宁城县期末)某中学为研究本校高三学生在市联考中的语文成绩,随机抽取了100位同学的语文成绩作为样本,得到以[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组的样本频率分布直方图如图.
(1)求直方图中x的值;
(2)请估计本次联考该校语文成绩的中位数和平均数;
(3)样本内语文分数在[130,140),[140,150]的两组学生中,用分层抽样的方法抽取5名学生,再从这5名学生中随机选出2人,求选出的两名学生中恰有一人成绩在[130,140)中的概率.
【解答】解:(1)由频率分布直方图得:(0.012+0.022+0.028+0.018+x+0.008+0.002)×10=1,
解得:x=0.01.
(2)由频率分布直方图知,分数在区间[80,100)、[80,110)的频率分别为0.34,0.62,因此,该校语文成绩的中位数m在[100,110)之间,
则(m﹣100)×0.028=0.16,
解得:m,
语文成绩的平均数为85×0.12+95×0.22+105×0.28+115×0.18+125×0.1+135×0.08+145×0.02=107.4,
所以该校语文成绩的中位数是,语文成绩的平均数是107.4.
(3)由频率分布直方图知,分数在[130,140),[140,150]内分别有8人和2人,
因此抽取的5人中,分数在[130,140)内有4人,在[140,150]内有1人,
记[130,140)内的4人为
a
,
b
,
c
,
d
,在[140,150]内的1人为
F
,
从5人中任取2人的结果有:ab,ac,ad,aF,bc,bd,bF,cd,cF,dF,共10个不同结果,它们等可能,
选出的2人中恰有一人成绩在[130,140)中的结果是:aF,bF,cF,dF,
所以选出的两名学生中恰有一人成绩在[130,140)中的概率是P.
18.(2024春 东坡区期末)在①,②,③sin2A﹣cos2B+cos2C=sinAsinB这三个条件中任选一个,补充在下面问题中,并完成解答.
在△ABC中,角A、B、C的对边分别为a、b、c,已知_____.
(1)求角C;
(2)若c=1,△ABC的面积,求△ABC的周长l的取值范围;
(3)若,,求tan∠ABD.
注:如果选择多个条件分别解答,按第一个解答计分.
【解答】解:(1)若选①:,
由正弦定理得,又sin(B+C)=sinA,
所以,又sinB>0,所以,即,
又0<C<π,所以;
若选②:因为,所以,
所以,所以,所以a2+b2﹣c2=ab,
所以,又0<C<π,所以;
若选③:因为sin2A﹣cos2B+cos2C=sin2A﹣(1﹣sin2B)+(1﹣sin2C)=sinAsinB,
即sin2A+sin2B﹣sin2C=sinAsinB,所以由正弦定理得a2+b2﹣c2=ab,
所以,又0<C<π,所以;
(2)因为△ABC的面积,所以,
由余弦定理得,即1=a2+b2﹣ab=(a+b)2﹣3ab,
所以,因为,所以,又c=1,
所以△ABC的周长l的取值范围为;
(3)因为,所以,所以,
又b<c,所以,,
,
又,所以,
记∠ABD=θ,在△BCD中,由正弦定理得:,
所以,
在△ABD中,由正弦定理得:,所以,
所以,所以,整理化简得,
所以,即tan∠ABD.
19.(2024春 达拉特旗校级期末)如图,在直三棱柱ABC﹣A1B1C1中,,AB=2AC=4,AC⊥CB,点D,E分别为棱BC,A1C1的中点,点F是线段CE的中点.
(1)求证:AF⊥平面BCE;
(2)求直线DF与平面ABF所成角的正弦值;
(3)求二面角F﹣AD﹣C的余弦值.
【解答】解:(1)在直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,又BC 平面ABC,所以AA1⊥BC,
又AC⊥CB,AC∩AA1=A,AC,AA1 平面ACC1A1,
所以BC⊥平面ACC1A1,
又AF 平面ACC1A1,
所以BC⊥AF,
在矩形ACC1A1中,,AC=2,点E是棱A1C1的中点,
所以AE=EC=2,所以△AEC是等边三角形,
又点F是线段CE的中点,所以AF⊥EC,
又CE∩BC=C,CE,BC 平面BCE,
所以AF⊥平面BCE.
(2)在平面BCE内,过点D作BF的垂线,垂足为H,
由(1)知AF⊥平面BCE,又DH 平面BCE,
所以AF⊥DH,
又BF⊥DH,BF∩AF=F,BF,AF 平面ABF,
所以DH⊥平面ABF,
所以∠DFB是直线DF与平面ABF所成角,
在△ABC中,AB=2AC=4,AC⊥CB,
所以,
又点D为棱BC的中点,所以,
因为BC⊥平面ACC1A1,又CE 平面ACC1A1,
所以BC⊥CE,
所以,,
在△BDF中,由余弦定理得,
所以,
即直线DF与平面ABF所成角的正弦值为.
(3)在平面ACC1A1内,过点F作AC的垂线,垂足为O,在平面ABC内,过O作AD的垂线,垂足为G,连接FG,
因为BC⊥平面ACC1A1,又FO 平面ACC1A1,所以BC⊥FO,
又AC⊥FO,AC∩BC=C,AC,BC 平面ABC,
所以FO⊥平面ABC,
又GO,AD 平面ABC,所以FO⊥GO,FO⊥AD,
又GO⊥AD,GO∩OF=O,GO,OF 平面GOF,
所以AD⊥平面GOF,
又GF 平面GOF,所以AD⊥GF,又GO⊥AD,
所以∠FGO为二面角F﹣AD﹣C的平面角,
在△FOC中,,
因为AF⊥平面BCE,DF 平面BCE,所以AF⊥FD,
又易得,FD=2,
所以,
由等面积法可知,
在△GFO中,FO⊥GO,,,
所以,
所以,
即二面角F﹣AD﹣C的余弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
一.选择题(共8小题)
1.(2024春 福建期末)已知非零向量,满足,且向量在向量上的投影向量是,则与的夹角是( )
A. B. C. D.
2.(2025春 滨湖区校级期末)已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A与B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
3.(2024春 武威期末)复数的虚部为( )
A. B. C.1 D.2
4.(2023春 河北期末)元宵节是春节之后的第一个重要节日,元宵节又称灯节,很多地区家家户户都挂花灯.下图是小明为自家设计的一个花灯,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为40cm和20cm,正六棱台与正六棱柱的高分别为10cm和60cm,则该花灯的体积为( )
A. B.
C. D.
5.(2024春 大通县期末)用2,3,4这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”发生的概率为( )
A. B. C. D.
6.(2024春 丽江期末)在平行四边形ABCD中(1,0),(2,1),则( )
A.4 B.﹣4 C.1 D.﹣1
7.(2024春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,则A1C1与B1C所成角为( )
A. B. C. D.
8.(2024春 海淀区校级期末)在△ABC中,若c=4,b﹣a=1,,则sinA为( )
A. B. C. D.
二.多选题(共3小题)
(多选)9.(2025春 漳州期末)如图正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且∠PCQ=45°,则( )
A.AP AQ=2PB QD
B.PQ<PB+QD
C.△APQ周长为定值
D.△APQ面积的最大值为
(多选)10.(2023春 福州期末)如图,平面四边形ABCD是由正方形AECD和直角三角形BCE组成的直角梯形,AD=1,,现将Rt△ACD沿斜边AC翻折成△ACD1(D1不在平面ABC内),若P为BC的中点,则在Rt△ACD翻折过程中,下列结论正确的是( )
A.AD1与BC可能垂直
B.三棱锥C﹣BD1E体积的最大值为
C.若A,C,E,D1都在同一球面上,则该球的表面积是2π
D.直线AD1与EP所成角的取值范围为
(多选)11.(2025春 海曙区校级期末)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O为正方体的中心,M为DD1的中点,F为侧面正方形AA1D1D内一动点,且满足B1F∥平面BC1M,则( )
A.三棱锥D1﹣DCB的外接球表面积为12π
B.动点F的轨迹是一条线段
C.三棱锥F﹣BC1M的体积是随点F的运动而变化的
D.若过A,M,C1三点作正方体的截面Ω,Q为截面Ω上一点,则线段A1Q长度的取值范围为
三.填空题(共3小题)
12.(2025春 静安区期末)连续抛掷一枚质地均匀的硬币4次,并记录朝上的一面是正面还是反面,则恰好出现正面与反面朝上都是2次的概率是 .
13.(2025春 宝山区期末)如图,以边长为1的正方形ABCD的各边为基准向外作正三角形,构成八边形AFBGCHDE.若点P、Q在八边形的内部(含边界),则的最小值为 .
14.(2024秋 宝山区校级期末)如图,已知直四棱柱ABCD﹣A1B1C1D1的所有棱长等于1,∠ABC=120°,O和O1分别是上下底面对角线的交点,H在线段OB1上,OH=3HB1,点M在线段BD上移动,则三棱锥M﹣C1O1H的体积最小值为 .
四.解答题(共5小题)
15.(2024春 锡林郭勒盟期末)已知向量,,
(Ⅰ)若,求实数x的值;
(Ⅱ)若,求向量与的夹角的余弦值.
16.(2023春 湘潭县期末)在△ABC中,设角A,B,C的对边长分别为a,b,c.
(1)若,,,求△ABC的周长;
(2)若点D是BC边上一点,且CD=2,BD=1,b2+2c2=9,求AD的长.
17.(2024秋 宁城县期末)某中学为研究本校高三学生在市联考中的语文成绩,随机抽取了100位同学的语文成绩作为样本,得到以[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组的样本频率分布直方图如图.
(1)求直方图中x的值;
(2)请估计本次联考该校语文成绩的中位数和平均数;
(3)样本内语文分数在[130,140),[140,150]的两组学生中,用分层抽样的方法抽取5名学生,再从这5名学生中随机选出2人,求选出的两名学生中恰有一人成绩在[130,140)中的概率.
18.(2024春 东坡区期末)在①,②,③sin2A﹣cos2B+cos2C=sinAsinB这三个条件中任选一个,补充在下面问题中,并完成解答.
在△ABC中,角A、B、C的对边分别为a、b、c,已知_____.
(1)求角C;
(2)若c=1,△ABC的面积,求△ABC的周长l的取值范围;
(3)若,,求tan∠ABD.
注:如果选择多个条件分别解答,按第一个解答计分.
19.(2024春 达拉特旗校级期末)如图,在直三棱柱ABC﹣A1B1C1中,,AB=2AC=4,AC⊥CB,点D,E分别为棱BC,A1C1的中点,点F是线段CE的中点.
(1)求证:AF⊥平面BCE;
(2)求直线DF与平面ABF所成角的正弦值;
(3)求二面角F﹣AD﹣C的余弦值.
期末真题重组练习卷-2024-2025学年高一数学下学期人教A版(2019)必修第二册
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 A B B C C C C B
二.多选题(共3小题)
题号 9 10 11
答案 AC ACD ABD
一.选择题(共8小题)
1.(2024春 福建期末)已知非零向量,满足,且向量在向量上的投影向量是,则与的夹角是( )
A. B. C. D.
【解答】解:因为,
所以,
所以,
因为向量在向量上的投影向量是,
所以,
即,所以,
又因为,
所以与的夹角是.
故选:A.
2.(2025春 滨湖区校级期末)已知事件A,B满足P(A)=0.5,P(B)=0.2,则( )
A.若B A,则P(AB)=0.5
B.若A与B互斥,则P(A+B)=0.7
C.若A与B相互独立,则
D.若P(B)+P(C)=1,则C与B相互对立
【解答】解:已知事件A,B满足P(A)=0.5,P(B)=0.2,
选项A:若B A,则P(AB)=P(B)=0.2,
选项B:若A与B互斥,则P(A+B)=0.7=P(A)+P(B).故选项B正确.
选项C:若A与B相互独立,则 A与相互独立,,故选项C错误.
选项D:若P(B)+P(C)=1,则由于不确定C与B是否互斥,所以无法确定两事件是否对立,故D错误.
故选:B.
3.(2024春 武威期末)复数的虚部为( )
A. B. C.1 D.2
【解答】解:,
则复数的虚部为.
故选:B.
4.(2023春 河北期末)元宵节是春节之后的第一个重要节日,元宵节又称灯节,很多地区家家户户都挂花灯.下图是小明为自家设计的一个花灯,该花灯由上面的正六棱台与下面的正六棱柱组成,若正六棱台的上、下两个底面的边长分别为40cm和20cm,正六棱台与正六棱柱的高分别为10cm和60cm,则该花灯的体积为( )
A. B.
C. D.
【解答】解:依题意,花灯的体积等于上面的正六棱台体积与下面的正六棱柱体积的和,
正六棱台的两个底面积分别为,,
所以花灯的体积.
故选:C.
5.(2024春 大通县期末)用2,3,4这3个数组成没有重复数字的三位数,则事件“这个三位数是偶数”发生的概率为( )
A. B. C. D.
【解答】解:将2,3,4组成一个没有重复数字的三位数的情况有{234,243,324,342,423,432},共6种,
其中偶数有{234,324,342,432},共4种,
所以事件“这个三位数是偶数”发生的概率为.
故选:C.
6.(2024春 丽江期末)在平行四边形ABCD中(1,0),(2,1),则( )
A.4 B.﹣4 C.1 D.﹣1
【解答】解:因为四边形ABCD为平行四边形,
所以,
所以.
故选:C.
7.(2024春 通州区期末)如图,在正方体ABCD﹣A1B1C1D1中,则A1C1与B1C所成角为( )
A. B. C. D.
【解答】解:连接DA1,DC1,
在正方体ABCD﹣A1B1C1D1中,
A1B1∥CD且A1B1=CD,
即四边形A1B1CD是平行四边形,
所以DA1∥B1C,
所以∠DA1C1即为A1C1与B1C所成角.
又△DA1C1是等边三角形,
即∠DA1C1=60°,
所以A1C1与B1C所成的角为.
故选:C.
8.(2024春 海淀区校级期末)在△ABC中,若c=4,b﹣a=1,,则sinA为( )
A. B. C. D.
【解答】解:由余弦定理知,c2=a2+b2﹣2abcosC,
所以42=a2+(a+1)2﹣2a (a+1) (),整理得a2+a﹣6=0,
解得a=2或a=﹣3,
由,知sinC,
由正弦定理知,,
所以,
所以sinA.
故选:B.
二.多选题(共3小题)
(多选)9.(2025春 漳州期末)如图正方形ABCD的边长为1,P,Q分别为边AB,DA上的点,且∠PCQ=45°,则( )
A.AP AQ=2PB QD
B.PQ<PB+QD
C.△APQ周长为定值
D.△APQ面积的最大值为
【解答】解:在正方形ABCD中,延长AD到E,使DE=BP,连接CE,
由S△APQ+2(S△PBC+S△QDC)=1,得,
于是(1﹣PB)(1﹣QD)+2PB+2QD=2,整理得PB+QD+PB QD=1,
2PB QD=1﹣PB﹣QD+PB QD=(1﹣PB)(1﹣QD)=AP AQ,所以A正确;
由正方形的性质可得Rt△CDE≌Rt△CBP,
∠ECD=∠PCB,CE=CP,由∠PCQ=45°,
得∠ECQ=∠ECD+∠DCQ=∠BCP+∠DCQ=45°=∠PCQ,
于是△ECQ≌△PCQ,PQ=QE=PB+QD,所以B错误;
△APQ周长为AP+AQ+PQ=1﹣PB+1﹣QD+PQ=2,所以C正确;
由C选项分析,2=AP+AQ2
=(2),
即AP AQ≤()2=6﹣4,
当且仅当AP=AQ时取等号,,所以D错误.
故选:AC.
(多选)10.(2023春 福州期末)如图,平面四边形ABCD是由正方形AECD和直角三角形BCE组成的直角梯形,AD=1,,现将Rt△ACD沿斜边AC翻折成△ACD1(D1不在平面ABC内),若P为BC的中点,则在Rt△ACD翻折过程中,下列结论正确的是( )
A.AD1与BC可能垂直
B.三棱锥C﹣BD1E体积的最大值为
C.若A,C,E,D1都在同一球面上,则该球的表面积是2π
D.直线AD1与EP所成角的取值范围为
【解答】解:对于A,由AD⊥CD,则AD1⊥CD1,当AD1⊥D1B时,且D1B<AB,
此时满足AD1⊥平面BCD1,因此AD1⊥BC,选项A正确;
对于B,取AC的中点O,连接OE,OD1,
则,且OD1⊥AC,
因为,
当平面ACD1⊥平面ABC时,三棱锥C﹣BD1E体积的最大值,
在Rt△BCE中,∠CBE,CE=1,则,
此时,
所以三棱锥C﹣BD1E体积的最大值为,选项B错误;
对于C,因为,
所以A,C,E,D1都在同一球面上,且球的半径为,
所以该球的表面积是,选项C正确;
对于D,作AM∥EP,因为P为BC的中点,所以EP=1,
因为,所以,
所以∠BAM=∠ABC=30°,所以∠MAC=15°,
AD1可以看成以AC为轴线,且母线和底面所成角是45°的圆锥的母线,
所以AC与AD1夹角为45°,AC与AM夹角为15°,又D1不在平面ABC内,
且60°=45°+15°,30°=45°﹣15°,
所以AD1与DM所成角的取值范围是,所以选项D正确,
故选:ACD.
(多选)11.(2025春 海曙区校级期末)如图,在棱长为2的正方体ABCD﹣A1B1C1D1中,O为正方体的中心,M为DD1的中点,F为侧面正方形AA1D1D内一动点,且满足B1F∥平面BC1M,则( )
A.三棱锥D1﹣DCB的外接球表面积为12π
B.动点F的轨迹是一条线段
C.三棱锥F﹣BC1M的体积是随点F的运动而变化的
D.若过A,M,C1三点作正方体的截面Ω,Q为截面Ω上一点,则线段A1Q长度的取值范围为
【解答】解:对于A,因为三棱锥D1﹣DCB的外接球与正方体ABCD﹣A1B1C1D1的外接球是同一个球,
因为正方体的外接球直径是正方体的体对角线,
设外接球半径为R,则2R=2,即R,
所以三棱锥D1﹣DCB的外接球表面积为4πR2=4π×3=12π,故A正确;
对于B,如图,分别取AA1,A1D1的中点H,G连接B1G,GH,HB1,AD1,
因为B1H∥C1M,B1H 平面BGH,C1M 平面BGH,
所以C1M∥平面BGH,
因为GH∥BC1,GH 平面BGH,BC1 平面BGH,
所以BC1∥平面BGH,
C1M 平面BC1M,BC1 平面BC1M,BC1∩C1M=C1,
所以平面B1GH∥平面BC1M,
而B1F∥平面BC1M,所以B1F 平面B1GH,所以点F轨迹为线段GH,故B正确;
由选项B可知,点F的轨迹为线段GH,因为GH∥平面BC1M,则点F到平面BC1M的距离为定值,
又△BC1M的面积为定值,从而可得三棱锥F﹣BC1M的体积是定值,故C不正确;
如图,设截面Ω与平面BAA1B1交于AN,N在BB1上,
因为截面Ω∩平面DAA1D1=AM,平面DAA1D1∥平面CBB1C1,
所以AM∥NC1,同理可证AN∥MC1,所以截面AMC1N为平行四边形,所以点N为BB1中点,
在四棱锥A1﹣AMC1N中,侧棱A1C1最长,且A1C1,设四棱锥A1﹣AMC1N的高为h,
因为AM=MC1,所以四边形AMC1N为菱形,
所以△AMC1的边AC1上的高为面对角线的一半,即为,又AC1,
则,,
所以,解得,
综上,可知线段A1Q长度的取值范围为,故D正确.
故选:ABD.
三.填空题(共3小题)
12.(2025春 静安区期末)连续抛掷一枚质地均匀的硬币4次,并记录朝上的一面是正面还是反面,则恰好出现正面与反面朝上都是2次的概率是 .
【解答】解:根据题意,连续抛掷一枚质地均匀的硬币4次,设正面向上的次数为X,则X=0、1、2、3、4,
易得X~B(4,),
若恰好出现正面与反面朝上都是2次,即X=2,则其概率P(X=2)()2(1)2.
故答案为:.
13.(2025春 宝山区期末)如图,以边长为1的正方形ABCD的各边为基准向外作正三角形,构成八边形AFBGCHDE.若点P、Q在八边形的内部(含边界),则的最小值为 .
【解答】解:由题意知, 的最小值为
||||cos∠FAH
=1cos135°
()
.
故答案为:.
14.(2024秋 宝山区校级期末)如图,已知直四棱柱ABCD﹣A1B1C1D1的所有棱长等于1,∠ABC=120°,O和O1分别是上下底面对角线的交点,H在线段OB1上,OH=3HB1,点M在线段BD上移动,则三棱锥M﹣C1O1H的体积最小值为 .
【解答】解:因为直四棱柱ABCD﹣A1B1C1D1的底面是菱形,∠ABC=120°,边长为1,
所以O1C1⊥平面BB1D1D,且,,
C1到平面BB1D1D的距离为,
因为OH=3HB1,点M是线段BD上的动点,
所以当△O1MH的面积取得最小值时,三棱锥C1﹣O1MH的体积有最小值.
将平面BB1D1D单独画图可得,
当M点到O1H的距离最小时,△O1MH的面积有最小值.
过点B作BF∥O1H,可得直线BF上方的点到O1H的距离比直线BF上的点到O1H的距离小,
而线段BD上除B点外的所有点都在直线BF下方,到O1H的距离比B点到O1H的距离大,
即当M点在B点时,△O1MH的面积取得最小值,且三棱锥C1﹣O1MH的体积有最小值.
连接O1B,则,
所以B1到O1B的距离,
因为OH=3HB1,
所以H到直线O1B的距离为,
所以,
所以.
故答案为:.
四.解答题(共5小题)
15.(2024春 锡林郭勒盟期末)已知向量,,
(Ⅰ)若,求实数x的值;
(Ⅱ)若,求向量与的夹角的余弦值.
【解答】解:(Ⅰ)已知向量,,
则,
又,
则(﹣4)×4=8(x﹣4),
即x=2;
(Ⅱ)由题意可得,
又,
则(﹣4)×(﹣2﹣x)+8×8=0,
即x=﹣18,
则,
则,
则向量与的夹角的余弦值为.
16.(2023春 湘潭县期末)在△ABC中,设角A,B,C的对边长分别为a,b,c.
(1)若,,,求△ABC的周长;
(2)若点D是BC边上一点,且CD=2,BD=1,b2+2c2=9,求AD的长.
【解答】解:(1)因为,,
所以.
由正弦定理,得,
所以.
(2)
设AD=x,在三角形ABD与三角形ACD中,由余弦定理得:
AB2=BD2+x2﹣2BD x cos∠ADB,AC2=CD2+x2﹣2CD x cos∠ADC,
所以12+x2﹣2x cos∠ADB=c2①,22+x2+4x cos∠ADB=b2②,
①×2+②得6+3x2=b2+2c2,
因为b2+2c2=9,所以6+3x2=9,解得x=1,
即AD的长为1.
17.(2024秋 宁城县期末)某中学为研究本校高三学生在市联考中的语文成绩,随机抽取了100位同学的语文成绩作为样本,得到以[80,90),[90,100),[100,110),[110,120),[120,130),[130,140),[140,150]分组的样本频率分布直方图如图.
(1)求直方图中x的值;
(2)请估计本次联考该校语文成绩的中位数和平均数;
(3)样本内语文分数在[130,140),[140,150]的两组学生中,用分层抽样的方法抽取5名学生,再从这5名学生中随机选出2人,求选出的两名学生中恰有一人成绩在[130,140)中的概率.
【解答】解:(1)由频率分布直方图得:(0.012+0.022+0.028+0.018+x+0.008+0.002)×10=1,
解得:x=0.01.
(2)由频率分布直方图知,分数在区间[80,100)、[80,110)的频率分别为0.34,0.62,因此,该校语文成绩的中位数m在[100,110)之间,
则(m﹣100)×0.028=0.16,
解得:m,
语文成绩的平均数为85×0.12+95×0.22+105×0.28+115×0.18+125×0.1+135×0.08+145×0.02=107.4,
所以该校语文成绩的中位数是,语文成绩的平均数是107.4.
(3)由频率分布直方图知,分数在[130,140),[140,150]内分别有8人和2人,
因此抽取的5人中,分数在[130,140)内有4人,在[140,150]内有1人,
记[130,140)内的4人为
a
,
b
,
c
,
d
,在[140,150]内的1人为
F
,
从5人中任取2人的结果有:ab,ac,ad,aF,bc,bd,bF,cd,cF,dF,共10个不同结果,它们等可能,
选出的2人中恰有一人成绩在[130,140)中的结果是:aF,bF,cF,dF,
所以选出的两名学生中恰有一人成绩在[130,140)中的概率是P.
18.(2024春 东坡区期末)在①,②,③sin2A﹣cos2B+cos2C=sinAsinB这三个条件中任选一个,补充在下面问题中,并完成解答.
在△ABC中,角A、B、C的对边分别为a、b、c,已知_____.
(1)求角C;
(2)若c=1,△ABC的面积,求△ABC的周长l的取值范围;
(3)若,,求tan∠ABD.
注:如果选择多个条件分别解答,按第一个解答计分.
【解答】解:(1)若选①:,
由正弦定理得,又sin(B+C)=sinA,
所以,又sinB>0,所以,即,
又0<C<π,所以;
若选②:因为,所以,
所以,所以,所以a2+b2﹣c2=ab,
所以,又0<C<π,所以;
若选③:因为sin2A﹣cos2B+cos2C=sin2A﹣(1﹣sin2B)+(1﹣sin2C)=sinAsinB,
即sin2A+sin2B﹣sin2C=sinAsinB,所以由正弦定理得a2+b2﹣c2=ab,
所以,又0<C<π,所以;
(2)因为△ABC的面积,所以,
由余弦定理得,即1=a2+b2﹣ab=(a+b)2﹣3ab,
所以,因为,所以,又c=1,
所以△ABC的周长l的取值范围为;
(3)因为,所以,所以,
又b<c,所以,,
,
又,所以,
记∠ABD=θ,在△BCD中,由正弦定理得:,
所以,
在△ABD中,由正弦定理得:,所以,
所以,所以,整理化简得,
所以,即tan∠ABD.
19.(2024春 达拉特旗校级期末)如图,在直三棱柱ABC﹣A1B1C1中,,AB=2AC=4,AC⊥CB,点D,E分别为棱BC,A1C1的中点,点F是线段CE的中点.
(1)求证:AF⊥平面BCE;
(2)求直线DF与平面ABF所成角的正弦值;
(3)求二面角F﹣AD﹣C的余弦值.
【解答】解:(1)在直三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,又BC 平面ABC,所以AA1⊥BC,
又AC⊥CB,AC∩AA1=A,AC,AA1 平面ACC1A1,
所以BC⊥平面ACC1A1,
又AF 平面ACC1A1,
所以BC⊥AF,
在矩形ACC1A1中,,AC=2,点E是棱A1C1的中点,
所以AE=EC=2,所以△AEC是等边三角形,
又点F是线段CE的中点,所以AF⊥EC,
又CE∩BC=C,CE,BC 平面BCE,
所以AF⊥平面BCE.
(2)在平面BCE内,过点D作BF的垂线,垂足为H,
由(1)知AF⊥平面BCE,又DH 平面BCE,
所以AF⊥DH,
又BF⊥DH,BF∩AF=F,BF,AF 平面ABF,
所以DH⊥平面ABF,
所以∠DFB是直线DF与平面ABF所成角,
在△ABC中,AB=2AC=4,AC⊥CB,
所以,
又点D为棱BC的中点,所以,
因为BC⊥平面ACC1A1,又CE 平面ACC1A1,
所以BC⊥CE,
所以,,
在△BDF中,由余弦定理得,
所以,
即直线DF与平面ABF所成角的正弦值为.
(3)在平面ACC1A1内,过点F作AC的垂线,垂足为O,在平面ABC内,过O作AD的垂线,垂足为G,连接FG,
因为BC⊥平面ACC1A1,又FO 平面ACC1A1,所以BC⊥FO,
又AC⊥FO,AC∩BC=C,AC,BC 平面ABC,
所以FO⊥平面ABC,
又GO,AD 平面ABC,所以FO⊥GO,FO⊥AD,
又GO⊥AD,GO∩OF=O,GO,OF 平面GOF,
所以AD⊥平面GOF,
又GF 平面GOF,所以AD⊥GF,又GO⊥AD,
所以∠FGO为二面角F﹣AD﹣C的平面角,
在△FOC中,,
因为AF⊥平面BCE,DF 平面BCE,所以AF⊥FD,
又易得,FD=2,
所以,
由等面积法可知,
在△GFO中,FO⊥GO,,,
所以,
所以,
即二面角F﹣AD﹣C的余弦值为.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
