期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)(含详解)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:13:13 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2025春 成都校级期末)以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A.DeepSeek B.ChatGPT
C.纳米AI D.微云人工智能
2.(2025春 成都校级期末)下列计算正确的是( )
A.(a2)3 (﹣a)=﹣a6 B.(﹣a3)2 a=a6
C.(﹣a2)3÷a=﹣a5 D.(﹣a3)2÷(﹣a)=a4
3.(2023秋 南召县期末)下列事件是必然事件的是( )
A.任意画一个三角形,其内角和为180°
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.投一次骰子,朝上的点数是6
4.(2024秋 南充期末)清代 袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )
A.8.4×10﹣5 B.8.4×10﹣6 C.8.4×10﹣7 D.8.4×106
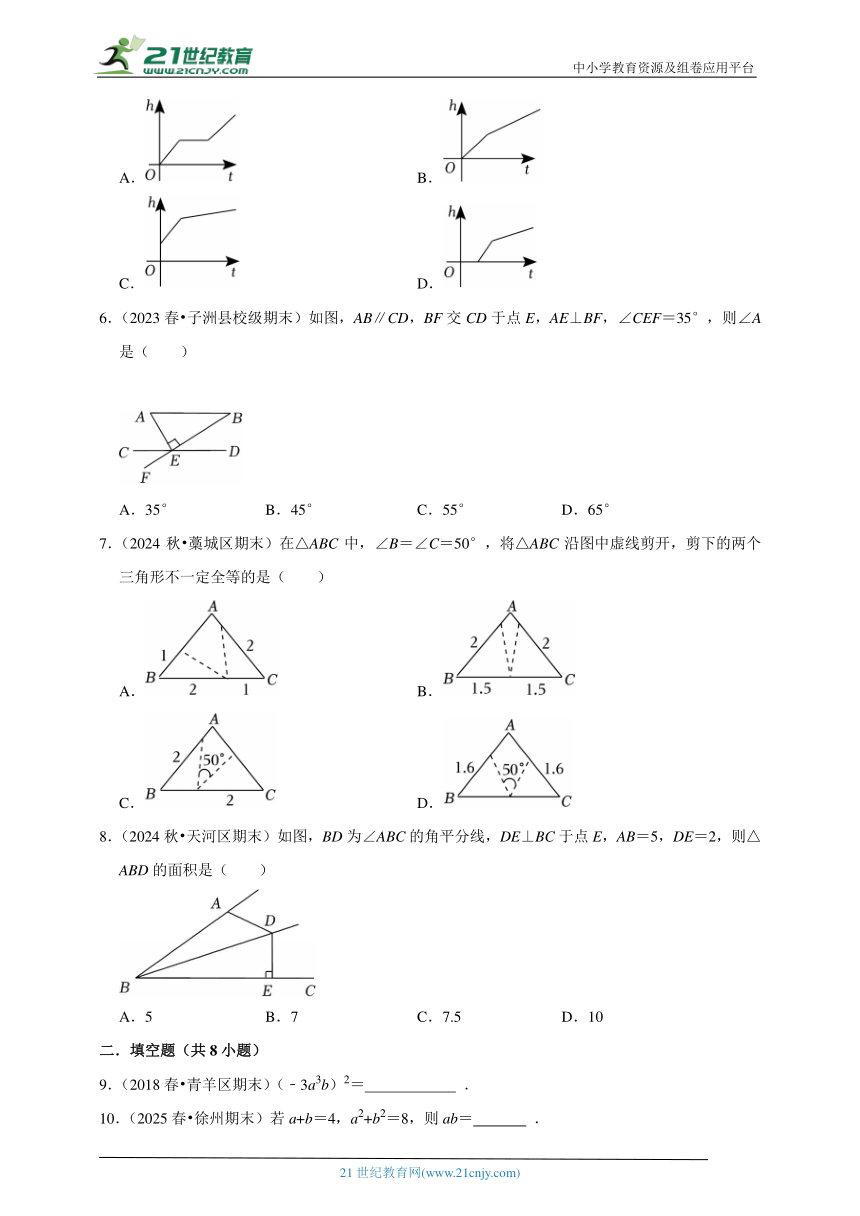
5.(2024春 永寿县期末)如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与时间注水时间t(s)的大致图象是( )
A. B.
C. D.
6.(2023春 子洲县校级期末)如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
7.(2024秋 藁城区期末)在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A. B.
C. D.
8.(2024秋 天河区期末)如图,BD为∠ABC的角平分线,DE⊥BC于点E,AB=5,DE=2,则△ABD的面积是( )
A.5 B.7 C.7.5 D.10
二.填空题(共8小题)
9.(2018春 青羊区期末)(﹣3a3b)2= .
10.(2025春 徐州期末)若a+b=4,a2+b2=8,则ab= .
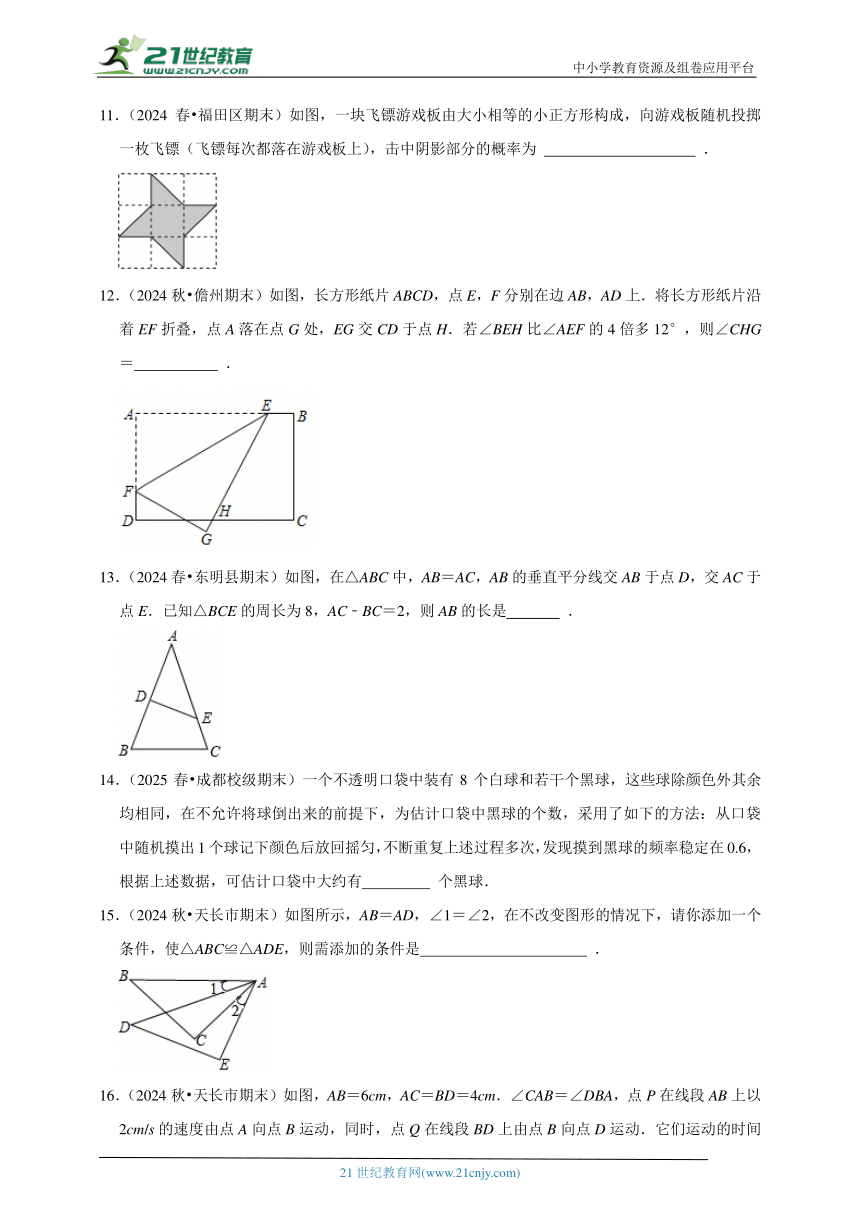
11.(2024春 福田区期末)如图,一块飞镖游戏板由大小相等的小正方形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),击中阴影部分的概率为 .
12.(2024秋 儋州期末)如图,长方形纸片ABCD,点E,F分别在边AB,AD上.将长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH比∠AEF的4倍多12°,则∠CHG= .
13.(2024春 东明县期末)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,AC﹣BC=2,则AB的长是 .
14.(2025春 成都校级期末)一个不透明口袋中装有8个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 个黑球.
15.(2024秋 天长市期末)如图所示,AB=AD,∠1=∠2,在不改变图形的情况下,请你添加一个条件,使△ABC≌△ADE,则需添加的条件是 .
16.(2024秋 天长市期末)如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为 .
三.解答题(共8小题)
17.(2023秋 崇明区期末)计算:(2x+3y)2﹣2x (2x﹣3y).
18.(2024春 碑林区期末)一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
19.(2024春 乌兰察布期末)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2= ( ).
又∵∠1=∠2,∴∠1=∠3( ).
∴AB∥ ( ).
∴∠BAC+ =180°( ).
∵∠BAC=70°,
∴∠AGD= .
20.(2024春 河源期末)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
21.(2024春 城关区校级期末)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
22.(2024春 永寿县期末)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为 米;李老师与家长聊天时间为 分钟;
(2)李老师的步行的速度是 米/分钟,跑步的速度是 米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
23.(2024秋 宁江区期末)如图,某市有一块长方形地块用来建造住宅、广场和商厦.住宅用地是长为(3a+2b)米,宽为4a米的长方形,广场是长为3a米,宽为(2a﹣b)米的长方形.
(1)这块用地的总面积是多少平方米?
(2)求出当a=30,b=50时商厦的用地面积.
24.(2024春 凤凰县期末)问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中AB∥CD,MG∥FN.点E,M,F在同一直线上,点G,N,H在同一直线上,且∠EFN=∠G.
(1)EF与GH平行吗?理由是什么?
(2)求证:∠AEF=∠GHD(提示:延长EF交CD于点P)
期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C A B D C D A
一.选择题(共8小题)
1.(2025春 成都校级期末)以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A.DeepSeek B.ChatGPT
C.纳米AI D.微云人工智能
【解答】解:A,B,C不是轴对称图形,D是轴对称图形,
故选:D.
2.(2025春 成都校级期末)下列计算正确的是( )
A.(a2)3 (﹣a)=﹣a6 B.(﹣a3)2 a=a6
C.(﹣a2)3÷a=﹣a5 D.(﹣a3)2÷(﹣a)=a4
【解答】解:根据同底数的幂相乘,底数不变指数相加;同底数的幂相除,底数不变指数相减;幂的乘方运算,底数不变指数相判断如下:
A.(a2)3 (﹣a)=a6 (﹣a)=﹣a7,故A错误.
B.(﹣a3)2 a=a6 a=a7,故B错误.
C.(﹣a2)3÷a=﹣a6÷a=﹣a5,故C正确.
D.(﹣a3)2÷(﹣a)=a6÷(﹣a)=﹣a5,故D错误.
故选:C.
3.(2023秋 南召县期末)下列事件是必然事件的是( )
A.任意画一个三角形,其内角和为180°
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.投一次骰子,朝上的点数是6
【解答】解:A、任意画一个三角形,其内角和为180°,是必然事件,故此选项符合题意;
B、球队员在罚球线上投篮一次,未投中,是随机事件,故此选项不符合题意;
C、经过有交通信号灯的路口,遇到红灯,是随机事件,故此选项不符合题意;
D、投一次骰子,朝上的点数是6,是随机事件,故此选项不符合题意.
故选:A.
4.(2024秋 南充期末)清代 袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )
A.8.4×10﹣5 B.8.4×10﹣6 C.8.4×10﹣7 D.8.4×106
【解答】解:0.0000084=8.4×10﹣6,
故选:B.
5.(2024春 永寿县期末)如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与时间注水时间t(s)的大致图象是( )
A. B.
C. D.
【解答】解:开始时向小烧杯中匀速注水,大烧杯的液面高度h(cm)为零,即h不会随时间t的增加而增大,故选项A、B、C不合题意;
当小烧杯满了后继续匀速注水,大烧杯的液面高度h(cm)随时间t的增加而增大,当小烧杯注满水后大烧杯的液面高度升高速度应该是由快到慢,故选项D符合题意.
故选:D.
6.(2023春 子洲县校级期末)如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
【解答】解:∵AE⊥BF,
∴∠AEF=90°,
∴∠AEC=90°﹣∠CEF=90°﹣35°=55°,
∵AB∥CD,
∴∠A=∠AEC=55°.
故选:C.
7.(2024秋 藁城区期末)在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A. B.
C. D.
【解答】解:A、根据SAS可以推出剪下的两个三角形全等,故A选项不符合题意;
B、根据SAS可以推出剪下的两个三角形全等,故B选项不符合题意;
C、如图:
∵∠DFC=∠DFE+∠EFC且∠DFC=∠B+∠BDF,
∴∠DFE+∠EFC=∠B+∠BDF,
∵∠B=∠DFE=50°,
∴∠EFC=∠BDF,
∵BD=FC,∠B=∠C,
∴△DBF≌△FCE(ASA).
根据ASA可以推出剪下的两个三角形全等,故C选项不符合题意;
D、如图:
由C选项可得:∠EFC=∠BDF,∠B=∠C,但FC不是两个角的夹边,所以两个三角形不一定全等,故D选项符合题意;
故选:D.
8.(2024秋 天河区期末)如图,BD为∠ABC的角平分线,DE⊥BC于点E,AB=5,DE=2,则△ABD的面积是( )
A.5 B.7 C.7.5 D.10
【解答】解:过D点作DH⊥AB于H,如图,
∵BD为∠ABC的角平分线,DE⊥BC,DH⊥AB,
∴DH=DE=2,
∴S△ABD5×2=5.
故选:A.
二.填空题(共8小题)
9.(2018春 青羊区期末)(﹣3a3b)2= 9a6b2 .
【解答】解:(﹣3a3b)2=9a6b2.
故答案为9a6b2.
10.(2025春 徐州期末)若a+b=4,a2+b2=8,则ab= 4 .
【解答】解:由条件可得,
故答案为:4.
11.(2024春 福田区期末)如图,一块飞镖游戏板由大小相等的小正方形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),击中阴影部分的概率为 .
【解答】解:∵游戏板的总面积为9个小正方形的面积,其中阴影部分面积为3个小正方形的面积,
∴飞镖落在阴影部分的概率是:,
故答案为:.
12.(2024秋 儋州期末)如图,长方形纸片ABCD,点E,F分别在边AB,AD上.将长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH比∠AEF的4倍多12°,则∠CHG= 124° .
【解答】解:由折叠的性质,可知:∠AEF=∠FEH.
∵∠BEH=4∠AEF+12°,∠AEF+∠FEH+∠BEH=180°,
∴∠AEF+∠AEF+4∠AEF+12°=180°,
∴∠AEF(180°﹣12°)=28°,
∴∠BEH=4∠AEF+12°=124°.
∵AB∥CD,
∴∠CHG=∠BEH=124°.
故答案为:124°.
13.(2024春 东明县期末)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,AC﹣BC=2,则AB的长是 5 .
【解答】解:如图所示:
∵△BCE的周长为8,
∴BE+EC+BC=8.
∵AB的垂直平分线交AB于点D,
∴AE=BE,
∴AE+EC+BC=8,
即AC+BC=8,
∵AC﹣BC=2,
∴AC=5,BC=3,
∵AB=AC,
∴AB=AC=5;
故答案为:5.
14.(2025春 成都校级期末)一个不透明口袋中装有8个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 12 个黑球.
【解答】解:由题意知,袋中球的总个数约为8÷(1﹣0.6)=20(个),
则口袋中黑球的个数约为20×0.6=12(个),
故答案为:12.
15.(2024秋 天长市期末)如图所示,AB=AD,∠1=∠2,在不改变图形的情况下,请你添加一个条件,使△ABC≌△ADE,则需添加的条件是 AC=AE或∠B=∠DA或∠ACB=∠AED(填对其中一个均可) .
【解答】解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
∵AB=AD,
∴根据SAS只要添加AC=AE即可,
根据ASA只要添加∠B=∠D即可,
根据AAS只要添加∠C=∠E即可.
故答案为:AC=AE或∠B=∠DA或∠ACB=∠AED
16.(2024秋 天长市期末)如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为 2或 .
【解答】解:当△ACP≌△BPQ,
∴AP=BQ,
∵运动时间相同,
∴P,Q的运动速度也相同,
∴x=2.
当△ACP≌△BQP时,
AC=BQ=4,PA=PB,
∴t=1.5,
∴x
故答案为2或.
三.解答题(共8小题)
17.(2023秋 崇明区期末)计算:(2x+3y)2﹣2x (2x﹣3y).
【解答】解:原式=4x2+12xy+9y2﹣4x2+6xy
=18xy+9y2.
18.(2024春 碑林区期末)一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
【解答】解:(1)∵一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,从袋中任取一个球是白球的概率是,
∴白球的个数为:29029(个),
设黑球的个数为x个,
则2x+3+x=290﹣29,
解得:x=86,
则2x+3=175,
答:袋中红球的个数为175个;
(2)由(1)得:从袋中任取一个球是黑球的概率为:.
19.(2024春 乌兰察布期末)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2= ∠3 ( 两直线平行,同位角相等 ).
又∵∠1=∠2,∴∠1=∠3( 等量代换 ).
∴AB∥ DG ( 内错角相等,两直线平行 ).
∴∠BAC+ ∠AGD =180°( 两直线平行,同旁内角互补 ).
∵∠BAC=70°,
∴∠AGD= 110° .
【解答】解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AB∥DG(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
20.(2024春 河源期末)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
【解答】(1)证明:∵E为AC中点,
∴AE=CE,
∵CF∥AB.
∴∠A=∠ACF,
在△AED 和△CEF中,
∴△AED≌△CEF(ASA);
(2)解:∵BE 平分∠ABC,∠ABE=25°,
∴∠ABC=2∠ABE=50°,
∵CF∥AB.
∴∠ABC+∠BCF=180°,∠A=∠ACF,
∴∠BCF=180°﹣∠ABC=130°,
∵CA平分∠BCF,
∴,
∴∠A=65°.
21.(2024春 城关区校级期末)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
【解答】解:(1)如图1,四边形ABCD即为所求.
(2)如图2,过点P作AB的垂线,交AB于点Q,
则点Q即为所求.
22.(2024春 永寿县期末)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为 1200 米;李老师与家长聊天时间为 5 分钟;
(2)李老师的步行的速度是 100 米/分钟,跑步的速度是 175 米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
【解答】解:(1)由李老师走过路程y(米)与出发后时间x(分钟)关系图可知李老师家与学校距离为1200米,
则10﹣5=5(分钟)
李老师与家长聊天时间经历了5分钟,
故答案为:1200;5;
(2)由李老师走过路程y(米)与出发后时间x(分钟)关系图可知,
李老师步行的速度为500÷5=100(米/分);
李老师跑步的速度为(1200﹣500)÷(14﹣10)=175(米/分),
答:步行速度100米/分;跑步的速度为175米/分.
(3)解:依题意,1200÷100=12(分)
14﹣12=2(分)
∴那么她比实际情况早到2分钟.
23.(2024秋 宁江区期末)如图,某市有一块长方形地块用来建造住宅、广场和商厦.住宅用地是长为(3a+2b)米,宽为4a米的长方形,广场是长为3a米,宽为(2a﹣b)米的长方形.
(1)这块用地的总面积是多少平方米?
(2)求出当a=30,b=50时商厦的用地面积.
【解答】解:(1)由题意,该块地是长方形,长为:3a+2b+(2a﹣b)=(5a+b)米,宽为4a(米),
∴这块用地的总面积为:(5a+b)×4a=(20a2+4ab)平方米.
(2)由题意得:商厦用地的宽为:2a﹣b=60﹣50=10(米),
长为:4a﹣3a=a=30(米).
∴商厦的用地面积为:30×10=300(平方米).
24.(2024春 凤凰县期末)问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中AB∥CD,MG∥FN.点E,M,F在同一直线上,点G,N,H在同一直线上,且∠EFN=∠G.
(1)EF与GH平行吗?理由是什么?
(2)求证:∠AEF=∠GHD(提示:延长EF交CD于点P)
【解答】解:(1)平行;理由如下:
∵MG∥FN,
∴∠EFN=∠EMG,
∵∠EFN=∠G,
∴∠G=∠EMG,
∴EF∥GH;
(2)延长EF交CD于点P,
∵AB∥CD,
∴∠BEF+∠MPH=180°,
∵EP∥GH,
∴∠GHP+∠MPH=180°,
∴∠BEF=∠GHP,
∵∠BEF=180°﹣∠AEF,∠GHP=180°﹣∠GHD,
∴∠AEF=∠GHD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)
一.选择题(共8小题)
1.(2025春 成都校级期末)以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A.DeepSeek B.ChatGPT
C.纳米AI D.微云人工智能
2.(2025春 成都校级期末)下列计算正确的是( )
A.(a2)3 (﹣a)=﹣a6 B.(﹣a3)2 a=a6
C.(﹣a2)3÷a=﹣a5 D.(﹣a3)2÷(﹣a)=a4
3.(2023秋 南召县期末)下列事件是必然事件的是( )
A.任意画一个三角形,其内角和为180°
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.投一次骰子,朝上的点数是6
4.(2024秋 南充期末)清代 袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )
A.8.4×10﹣5 B.8.4×10﹣6 C.8.4×10﹣7 D.8.4×106
5.(2024春 永寿县期末)如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与时间注水时间t(s)的大致图象是( )
A. B.
C. D.
6.(2023春 子洲县校级期末)如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
7.(2024秋 藁城区期末)在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A. B.
C. D.
8.(2024秋 天河区期末)如图,BD为∠ABC的角平分线,DE⊥BC于点E,AB=5,DE=2,则△ABD的面积是( )
A.5 B.7 C.7.5 D.10
二.填空题(共8小题)
9.(2018春 青羊区期末)(﹣3a3b)2= .
10.(2025春 徐州期末)若a+b=4,a2+b2=8,则ab= .
11.(2024春 福田区期末)如图,一块飞镖游戏板由大小相等的小正方形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),击中阴影部分的概率为 .
12.(2024秋 儋州期末)如图,长方形纸片ABCD,点E,F分别在边AB,AD上.将长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH比∠AEF的4倍多12°,则∠CHG= .
13.(2024春 东明县期末)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,AC﹣BC=2,则AB的长是 .
14.(2025春 成都校级期末)一个不透明口袋中装有8个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 个黑球.
15.(2024秋 天长市期末)如图所示,AB=AD,∠1=∠2,在不改变图形的情况下,请你添加一个条件,使△ABC≌△ADE,则需添加的条件是 .
16.(2024秋 天长市期末)如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为 .
三.解答题(共8小题)
17.(2023秋 崇明区期末)计算:(2x+3y)2﹣2x (2x﹣3y).
18.(2024春 碑林区期末)一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
19.(2024春 乌兰察布期末)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2= ( ).
又∵∠1=∠2,∴∠1=∠3( ).
∴AB∥ ( ).
∴∠BAC+ =180°( ).
∵∠BAC=70°,
∴∠AGD= .
20.(2024春 河源期末)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
21.(2024春 城关区校级期末)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
22.(2024春 永寿县期末)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为 米;李老师与家长聊天时间为 分钟;
(2)李老师的步行的速度是 米/分钟,跑步的速度是 米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
23.(2024秋 宁江区期末)如图,某市有一块长方形地块用来建造住宅、广场和商厦.住宅用地是长为(3a+2b)米,宽为4a米的长方形,广场是长为3a米,宽为(2a﹣b)米的长方形.
(1)这块用地的总面积是多少平方米?
(2)求出当a=30,b=50时商厦的用地面积.
24.(2024春 凤凰县期末)问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中AB∥CD,MG∥FN.点E,M,F在同一直线上,点G,N,H在同一直线上,且∠EFN=∠G.
(1)EF与GH平行吗?理由是什么?
(2)求证:∠AEF=∠GHD(提示:延长EF交CD于点P)
期末真题重组练习卷-2024-2025学年数学七年级下册北师大版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D C A B D C D A
一.选择题(共8小题)
1.(2025春 成都校级期末)以下是四款常用的人工智能大模型的图标,其文字上方的图案是轴对称图形的是( )
A.DeepSeek B.ChatGPT
C.纳米AI D.微云人工智能
【解答】解:A,B,C不是轴对称图形,D是轴对称图形,
故选:D.
2.(2025春 成都校级期末)下列计算正确的是( )
A.(a2)3 (﹣a)=﹣a6 B.(﹣a3)2 a=a6
C.(﹣a2)3÷a=﹣a5 D.(﹣a3)2÷(﹣a)=a4
【解答】解:根据同底数的幂相乘,底数不变指数相加;同底数的幂相除,底数不变指数相减;幂的乘方运算,底数不变指数相判断如下:
A.(a2)3 (﹣a)=a6 (﹣a)=﹣a7,故A错误.
B.(﹣a3)2 a=a6 a=a7,故B错误.
C.(﹣a2)3÷a=﹣a6÷a=﹣a5,故C正确.
D.(﹣a3)2÷(﹣a)=a6÷(﹣a)=﹣a5,故D错误.
故选:C.
3.(2023秋 南召县期末)下列事件是必然事件的是( )
A.任意画一个三角形,其内角和为180°
B.篮球队员在罚球线上投篮一次,未投中
C.经过有交通信号灯的路口,遇到红灯
D.投一次骰子,朝上的点数是6
【解答】解:A、任意画一个三角形,其内角和为180°,是必然事件,故此选项符合题意;
B、球队员在罚球线上投篮一次,未投中,是随机事件,故此选项不符合题意;
C、经过有交通信号灯的路口,遇到红灯,是随机事件,故此选项不符合题意;
D、投一次骰子,朝上的点数是6,是随机事件,故此选项不符合题意.
故选:A.
4.(2024秋 南充期末)清代 袁枚的一首诗《苔》中的诗句:“白日不到处,青春恰自来.苔花如米小,也学牡丹开.”若苔花的花粉直径约为0.0000084米,则数据0.0000084用科学记数法表示为( )
A.8.4×10﹣5 B.8.4×10﹣6 C.8.4×10﹣7 D.8.4×106
【解答】解:0.0000084=8.4×10﹣6,
故选:B.
5.(2024春 永寿县期末)如图,在大烧杯中放了一个小烧杯,现向小烧杯中匀速注水,小烧杯满了后继续匀速注水,则大烧杯的液面高度h(cm)与时间注水时间t(s)的大致图象是( )
A. B.
C. D.
【解答】解:开始时向小烧杯中匀速注水,大烧杯的液面高度h(cm)为零,即h不会随时间t的增加而增大,故选项A、B、C不合题意;
当小烧杯满了后继续匀速注水,大烧杯的液面高度h(cm)随时间t的增加而增大,当小烧杯注满水后大烧杯的液面高度升高速度应该是由快到慢,故选项D符合题意.
故选:D.
6.(2023春 子洲县校级期末)如图,AB∥CD,BF交CD于点E,AE⊥BF,∠CEF=35°,则∠A是( )
A.35° B.45° C.55° D.65°
【解答】解:∵AE⊥BF,
∴∠AEF=90°,
∴∠AEC=90°﹣∠CEF=90°﹣35°=55°,
∵AB∥CD,
∴∠A=∠AEC=55°.
故选:C.
7.(2024秋 藁城区期末)在△ABC中,∠B=∠C=50°,将△ABC沿图中虚线剪开,剪下的两个三角形不一定全等的是( )
A. B.
C. D.
【解答】解:A、根据SAS可以推出剪下的两个三角形全等,故A选项不符合题意;
B、根据SAS可以推出剪下的两个三角形全等,故B选项不符合题意;
C、如图:
∵∠DFC=∠DFE+∠EFC且∠DFC=∠B+∠BDF,
∴∠DFE+∠EFC=∠B+∠BDF,
∵∠B=∠DFE=50°,
∴∠EFC=∠BDF,
∵BD=FC,∠B=∠C,
∴△DBF≌△FCE(ASA).
根据ASA可以推出剪下的两个三角形全等,故C选项不符合题意;
D、如图:
由C选项可得:∠EFC=∠BDF,∠B=∠C,但FC不是两个角的夹边,所以两个三角形不一定全等,故D选项符合题意;
故选:D.
8.(2024秋 天河区期末)如图,BD为∠ABC的角平分线,DE⊥BC于点E,AB=5,DE=2,则△ABD的面积是( )
A.5 B.7 C.7.5 D.10
【解答】解:过D点作DH⊥AB于H,如图,
∵BD为∠ABC的角平分线,DE⊥BC,DH⊥AB,
∴DH=DE=2,
∴S△ABD5×2=5.
故选:A.
二.填空题(共8小题)
9.(2018春 青羊区期末)(﹣3a3b)2= 9a6b2 .
【解答】解:(﹣3a3b)2=9a6b2.
故答案为9a6b2.
10.(2025春 徐州期末)若a+b=4,a2+b2=8,则ab= 4 .
【解答】解:由条件可得,
故答案为:4.
11.(2024春 福田区期末)如图,一块飞镖游戏板由大小相等的小正方形构成,向游戏板随机投掷一枚飞镖(飞镖每次都落在游戏板上),击中阴影部分的概率为 .
【解答】解:∵游戏板的总面积为9个小正方形的面积,其中阴影部分面积为3个小正方形的面积,
∴飞镖落在阴影部分的概率是:,
故答案为:.
12.(2024秋 儋州期末)如图,长方形纸片ABCD,点E,F分别在边AB,AD上.将长方形纸片沿着EF折叠,点A落在点G处,EG交CD于点H.若∠BEH比∠AEF的4倍多12°,则∠CHG= 124° .
【解答】解:由折叠的性质,可知:∠AEF=∠FEH.
∵∠BEH=4∠AEF+12°,∠AEF+∠FEH+∠BEH=180°,
∴∠AEF+∠AEF+4∠AEF+12°=180°,
∴∠AEF(180°﹣12°)=28°,
∴∠BEH=4∠AEF+12°=124°.
∵AB∥CD,
∴∠CHG=∠BEH=124°.
故答案为:124°.
13.(2024春 东明县期末)如图,在△ABC中,AB=AC,AB的垂直平分线交AB于点D,交AC于点E.已知△BCE的周长为8,AC﹣BC=2,则AB的长是 5 .
【解答】解:如图所示:
∵△BCE的周长为8,
∴BE+EC+BC=8.
∵AB的垂直平分线交AB于点D,
∴AE=BE,
∴AE+EC+BC=8,
即AC+BC=8,
∵AC﹣BC=2,
∴AC=5,BC=3,
∵AB=AC,
∴AB=AC=5;
故答案为:5.
14.(2025春 成都校级期末)一个不透明口袋中装有8个白球和若干个黑球,这些球除颜色外其余均相同,在不允许将球倒出来的前提下,为估计口袋中黑球的个数,采用了如下的方法:从口袋中随机摸出1个球记下颜色后放回摇匀,不断重复上述过程多次,发现摸到黑球的频率稳定在0.6,根据上述数据,可估计口袋中大约有 12 个黑球.
【解答】解:由题意知,袋中球的总个数约为8÷(1﹣0.6)=20(个),
则口袋中黑球的个数约为20×0.6=12(个),
故答案为:12.
15.(2024秋 天长市期末)如图所示,AB=AD,∠1=∠2,在不改变图形的情况下,请你添加一个条件,使△ABC≌△ADE,则需添加的条件是 AC=AE或∠B=∠DA或∠ACB=∠AED(填对其中一个均可) .
【解答】解:∵∠1=∠2,
∴∠1+∠DAC=∠2+∠DAC,
即∠BAC=∠DAE,
∵AB=AD,
∴根据SAS只要添加AC=AE即可,
根据ASA只要添加∠B=∠D即可,
根据AAS只要添加∠C=∠E即可.
故答案为:AC=AE或∠B=∠DA或∠ACB=∠AED
16.(2024秋 天长市期末)如图,AB=6cm,AC=BD=4cm.∠CAB=∠DBA,点P在线段AB上以2cm/s的速度由点A向点B运动,同时,点Q在线段BD上由点B向点D运动.它们运动的时间为t(s).设点Q的运动速度为xcm/s,若使得△ACP与△BPQ全等,则x的值为 2或 .
【解答】解:当△ACP≌△BPQ,
∴AP=BQ,
∵运动时间相同,
∴P,Q的运动速度也相同,
∴x=2.
当△ACP≌△BQP时,
AC=BQ=4,PA=PB,
∴t=1.5,
∴x
故答案为2或.
三.解答题(共8小题)
17.(2023秋 崇明区期末)计算:(2x+3y)2﹣2x (2x﹣3y).
【解答】解:原式=4x2+12xy+9y2﹣4x2+6xy
=18xy+9y2.
18.(2024春 碑林区期末)一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,若红球个数是黑球个数的2倍多3个,从袋中任取一个球是白球的概率是.
(1)求袋中红球的个数.
(2)求从袋中任取一个球是黑球的概率.
【解答】解:(1)∵一个口袋中放有290个涂有红、黑、白三种色的质地相同的小球,从袋中任取一个球是白球的概率是,
∴白球的个数为:29029(个),
设黑球的个数为x个,
则2x+3+x=290﹣29,
解得:x=86,
则2x+3=175,
答:袋中红球的个数为175个;
(2)由(1)得:从袋中任取一个球是黑球的概率为:.
19.(2024春 乌兰察布期末)如图,EF∥AD,∠1=∠2,∠BAC=70°,求∠AGD的度数.
解:∵EF∥AD,
∴∠2= ∠3 ( 两直线平行,同位角相等 ).
又∵∠1=∠2,∴∠1=∠3( 等量代换 ).
∴AB∥ DG ( 内错角相等,两直线平行 ).
∴∠BAC+ ∠AGD =180°( 两直线平行,同旁内角互补 ).
∵∠BAC=70°,
∴∠AGD= 110° .
【解答】解:∵EF∥AD,
∴∠2=∠3(两直线平行,同位角相等).
又∵∠1=∠2,
∴∠1=∠3(等量代换).
∴AB∥DG(内错角相等,两直线平行).
∴∠BAC+∠AGD=180°(两直线平行,同旁内角互补).
∵∠BAC=70°,
∴∠AGD=110°.
故答案为:∠3;两直线平行,同位角相等;等量代换;DG;内错角相等,两直线平行;∠AGD;两直线平行,同旁内角互补;110°.
20.(2024春 河源期末)如图,在△ABC中,D为AB上一点,E为AC中点,连接DE并延长至点F,使得CF∥AB.
(1)求证:△AED≌△CEF;
(2)连接BE,若BE平分∠ABC,CA平分∠BCF,且∠ABE=25°,求∠A的度数.
【解答】(1)证明:∵E为AC中点,
∴AE=CE,
∵CF∥AB.
∴∠A=∠ACF,
在△AED 和△CEF中,
∴△AED≌△CEF(ASA);
(2)解:∵BE 平分∠ABC,∠ABE=25°,
∴∠ABC=2∠ABE=50°,
∵CF∥AB.
∴∠ABC+∠BCF=180°,∠A=∠ACF,
∴∠BCF=180°﹣∠ABC=130°,
∵CA平分∠BCF,
∴,
∴∠A=65°.
21.(2024春 城关区校级期末)如图是4×4的正方形网格,请仅用无刻度尺的直尺按要求完成以下作图.
(1)在图1中作四边形ABCD,使点C,D在格点上,并且四边形ABCD为轴对称图形.(画出一种即可)
(2)在图2中的线段AB上作点Q,使PQ最短.(用实线保留作图痕迹)
【解答】解:(1)如图1,四边形ABCD即为所求.
(2)如图2,过点P作AB的垂线,交AB于点Q,
则点Q即为所求.
22.(2024春 永寿县期末)李老师为锻炼身体一直坚持步行上下班,一天早上李老师从家出发步行前往学校,途中遇到一位家长,同他聊了一会儿,之后便跑步到学校,这一过程李老师走过的路程y(米)与出发后时间x(分钟)关系如图所示.
(1)李老师家与学校距离为 1200 米;李老师与家长聊天时间为 5 分钟;
(2)李老师的步行的速度是 100 米/分钟,跑步的速度是 175 米/分钟;
(3)如果李老师没有遇到家长,一直步行到校,那么她比实际情况早到多少分钟?
【解答】解:(1)由李老师走过路程y(米)与出发后时间x(分钟)关系图可知李老师家与学校距离为1200米,
则10﹣5=5(分钟)
李老师与家长聊天时间经历了5分钟,
故答案为:1200;5;
(2)由李老师走过路程y(米)与出发后时间x(分钟)关系图可知,
李老师步行的速度为500÷5=100(米/分);
李老师跑步的速度为(1200﹣500)÷(14﹣10)=175(米/分),
答:步行速度100米/分;跑步的速度为175米/分.
(3)解:依题意,1200÷100=12(分)
14﹣12=2(分)
∴那么她比实际情况早到2分钟.
23.(2024秋 宁江区期末)如图,某市有一块长方形地块用来建造住宅、广场和商厦.住宅用地是长为(3a+2b)米,宽为4a米的长方形,广场是长为3a米,宽为(2a﹣b)米的长方形.
(1)这块用地的总面积是多少平方米?
(2)求出当a=30,b=50时商厦的用地面积.
【解答】解:(1)由题意,该块地是长方形,长为:3a+2b+(2a﹣b)=(5a+b)米,宽为4a(米),
∴这块用地的总面积为:(5a+b)×4a=(20a2+4ab)平方米.
(2)由题意得:商厦用地的宽为:2a﹣b=60﹣50=10(米),
长为:4a﹣3a=a=30(米).
∴商厦的用地面积为:30×10=300(平方米).
24.(2024春 凤凰县期末)问题:中国汉字博大精深,方块文字智慧灵秀,奥妙无穷,如图(1)是一个“互”字,如图(2)是由图(1)抽象的几何图形,其中AB∥CD,MG∥FN.点E,M,F在同一直线上,点G,N,H在同一直线上,且∠EFN=∠G.
(1)EF与GH平行吗?理由是什么?
(2)求证:∠AEF=∠GHD(提示:延长EF交CD于点P)
【解答】解:(1)平行;理由如下:
∵MG∥FN,
∴∠EFN=∠EMG,
∵∠EFN=∠G,
∴∠G=∠EMG,
∴EF∥GH;
(2)延长EF交CD于点P,
∵AB∥CD,
∴∠BEF+∠MPH=180°,
∵EP∥GH,
∴∠GHP+∠MPH=180°,
∴∠BEF=∠GHP,
∵∠BEF=180°﹣∠AEF,∠GHP=180°﹣∠GHD,
∴∠AEF=∠GHD.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
