期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)(含详解)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:43:07 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024春 余干县校级期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
2.(2024春 七星关区校级期末)一把直尺和一个含30°角的直角三角板按如图方式放置,若∠1=25°,则∠2=( )
A.25° B.30° C.35° D.45°
3.(2022秋 江北区校级期末)如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
4.(2025春 五华区校级期末)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOB=45°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
5.(2024秋 长安区期末)“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则2x+y的值为( )
A.﹣5 B.﹣4 C.4 D.5
6.(2025春 上海期末)在下列方程组中,属于二元一次方程组的是( )
A. B.
C. D.
7.(2025春 五华区校级期末)如果点A(m﹣8,m﹣2)在x轴上,那么点B(m+1,m﹣6)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.(2025春 隆昌市校级期末)关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
二.填空题(共8小题)
9.(2024春 硚口区期末)写出一个小于3的正无理数 .
10.(2021秋 开化县期末)不等式3x﹣1<5的解集为 .
11.(2024春 张店区期末)比较大小:2 (填“>”、“<”或“=”).
12.(2025春 五华区校级期末)为了估计学校池塘中鱼的数量,九年级一班的同学采用如下方法:从池塘中捕上50条鱼做上标记,然后放回池塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再捕上50条,若其中带有标记的鱼有10条,则池塘中鱼估计有 条.
13.(2025春 虹口区校级期末)关于x,y的方程组有无数组解,则ab= .
14.(2025春 五华区校级期末)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为 .
15.(2025春 上海期末)某班级同学分组,若每组5人则余3人,若每组6人则缺5人.设班级人数为x人,组数为y组,则列方程组为 .
16.(2024秋 朝阳区校级期末)如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= .
三.解答题(共10小题)
17.(2025春 吐鲁番市期末)计算:.
18.(2025春 上海期末)(1)解方程组:;
(2)解方程组:.
19.(2023秋 高新区校级期末)解不等式,并把不等式的解集在数轴上表示出来.
20.(2024秋 东坡区期末)解不等式组:,将其解集在数轴上表示出来,并写出所有的整数解.
21.(2025春 五华区校级期末)如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)求证:∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
22.(2024秋 西安期末)如果一个正数m的两个平方根分别是2a﹣3和a﹣9,n+2的算术平方根是1.
(1)求m和n的值.
(2)求m﹣11n的算术平方根.
23.(2024秋 榆树市期末)完成下面的证明:
如图,已知AB∥EF,EP⊥EQ,∠1+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE= ( ).
∵EP⊥EQ,
∴∠PEQ= ( ).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1= .
∴ ∥CD( ).
又∵AB∥EF,
∴AB∥CD( ).
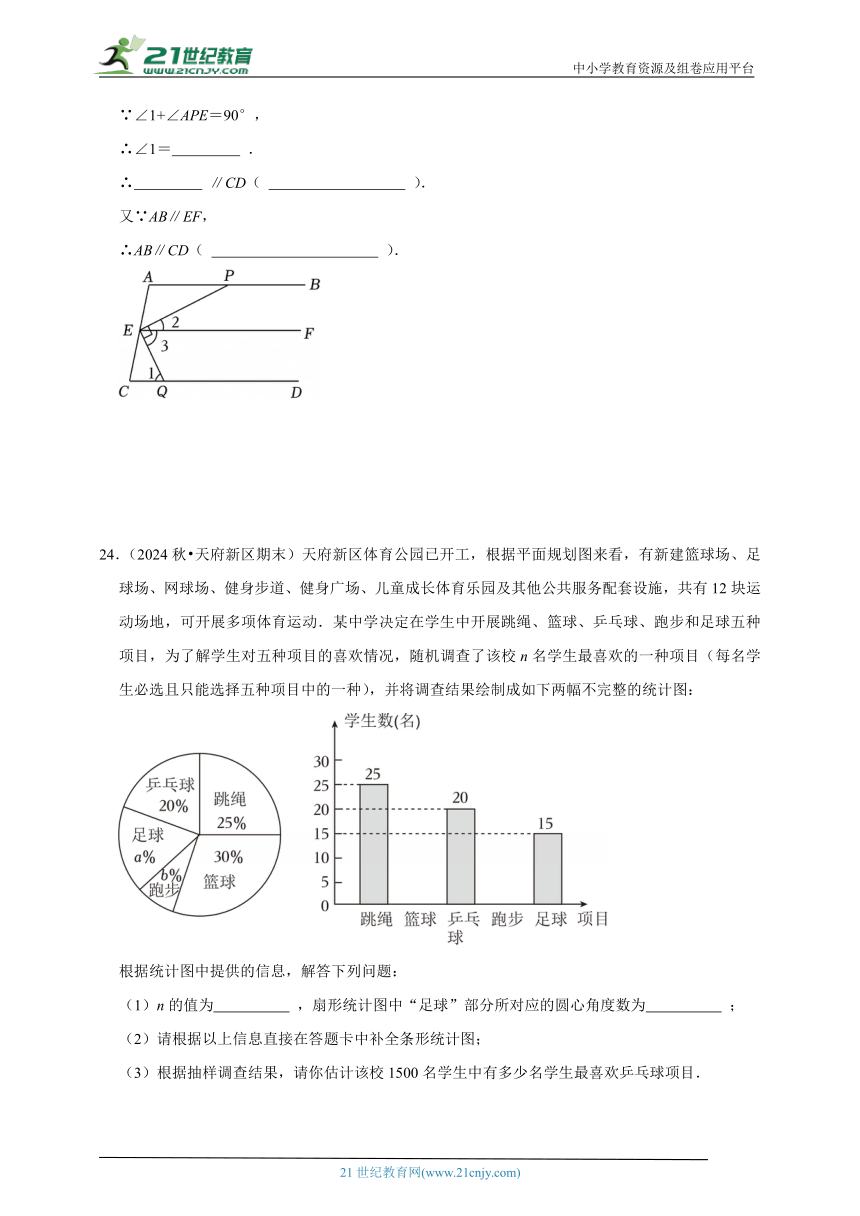
24.(2024秋 天府新区期末)天府新区体育公园已开工,根据平面规划图来看,有新建篮球场、足球场、网球场、健身步道、健身广场、儿童成长体育乐园及其他公共服务配套设施,共有12块运动场地,可开展多项体育运动.某中学决定在学生中开展跳绳、篮球、乒乓球、跑步和足球五种项目,为了解学生对五种项目的喜欢情况,随机调查了该校n名学生最喜欢的一种项目(每名学生必选且只能选择五种项目中的一种),并将调查结果绘制成如下两幅不完整的统计图:
根据统计图中提供的信息,解答下列问题:
(1)n的值为 ,扇形统计图中“足球”部分所对应的圆心角度数为 ;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计该校1500名学生中有多少名学生最喜欢乒乓球项目.
25.(2024秋 长沙期末)“文房四宝”是中国独有的书法绘画工具,即笔、墨、纸、砚,文房四宝之名,起源于南北朝时期.我校为了落实双减政策,丰富学生的课后服务活动,开设了书法社团,计划为学生购买甲、乙两种型号“文房四宝”,经过调查得知:每套甲型号“文房四宝”的价格比每套乙型号的价格贵30元,买5套甲型号“文房四宝”和10套乙型号“文房四宝”共用900元.
(1)求每套甲、乙型号“文房四宝”的价格分别是多少?
(2)若学校需购进甲、乙两种型号“文房四宝”共100套,总费用不超过5870元,并且根据学生需求,要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍,请问共有几种购买方案?最低费用是多少?
26.(2024秋 沈阳期末)【发现问题】
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
【提出问题】
小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= °(不需要写解答过程)
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C C B C D B
一.选择题(共8小题)
1.(2024春 余干县校级期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【解答】解:∵,3,
而,
∴2,
∴估计的值在2和3之间.
故选:B.
2.(2024春 七星关区校级期末)一把直尺和一个含30°角的直角三角板按如图方式放置,若∠1=25°,则∠2=( )
A.25° B.30° C.35° D.45°
【解答】解:如图,
∵AB∥CD,
∴∠1=∠ABC=25°,
∵∠MBC=60°,
∴∠2=∠MBC﹣∠ABC=35°,
故选:C.
3.(2022秋 江北区校级期末)如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
【解答】解:∵OP是∠AOB的平分线,∠AOB=30°,
∴∠POA∠AOB=15°,
∵PC∥OA,
∴∠CPO=∠POA=15°.
故选:C.
4.(2025春 五华区校级期末)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOB=45°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
【解答】解:∵直线AB,CD相交于点O,∠DOB=45°,
∴∠AOC=∠DOB=45°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=∠AOE﹣∠AOC=90°﹣45°=45°.
故选:C.
5.(2024秋 长安区期末)“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则2x+y的值为( )
A.﹣5 B.﹣4 C.4 D.5
【解答】解:由题意得:,
解得:,
∴2x+y=2×(﹣3)+2=﹣4,
故选:B.
6.(2025春 上海期末)在下列方程组中,属于二元一次方程组的是( )
A. B.
C. D.
【解答】解:A、是三元一次方程组,故选项不符合题意;
B、是二元二次方程组,故选项不符合题意;
C、是二元一次方程组,故选项符合题意;
D、是分式方程组,故选项不符合题意;
故选:C.
7.(2025春 五华区校级期末)如果点A(m﹣8,m﹣2)在x轴上,那么点B(m+1,m﹣6)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由题意得,m﹣2=0,
解得,m=2,
∴m+1=3,m﹣6=﹣4,
∴B(m+1,m﹣6)在第四象限.
故选:D.
8.(2025春 隆昌市校级期末)关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
【解答】解:,
由①得:y>﹣2,
由②得:y<a,
∴原不等式组的解集为﹣2<y<a,
∵关于y的一元一次不等式组有3个整数解,
∴1<a≤2,
故选:B.
二.填空题(共8小题)
9.(2024春 硚口区期末)写出一个小于3的正无理数 (答案不唯一) .
【解答】解:本题答案不唯一:如等.
故答案为:(答案不唯一).
10.(2021秋 开化县期末)不等式3x﹣1<5的解集为 x<2 .
【解答】解:3x﹣1<5,
3x<6,
x<2.
故答案为:x<2.
11.(2024春 张店区期末)比较大小:2 < (填“>”、“<”或“=”).
【解答】解:∵2,
∴,
∴2;
故答案为:<.
12.(2025春 五华区校级期末)为了估计学校池塘中鱼的数量,九年级一班的同学采用如下方法:从池塘中捕上50条鱼做上标记,然后放回池塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再捕上50条,若其中带有标记的鱼有10条,则池塘中鱼估计有 250 条.
【解答】解:池塘中鱼估计有:50250(条),
故答案为:250.
13.(2025春 虹口区校级期末)关于x,y的方程组有无数组解,则ab= .
【解答】解:因为关于x,y的方程组有无数组解,
设比例系数k,
所以,﹣1=3bk,1=2k,
解得:,a=1,b,
所以ab.
故答案为:.
14.(2025春 五华区校级期末)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为 51 .
【解答】解:∵S△ABC=S△DEF,
∴S阴=S梯形ABEH (10+7)×6=51
故答案为:51.
15.(2025春 上海期末)某班级同学分组,若每组5人则余3人,若每组6人则缺5人.设班级人数为x人,组数为y组,则列方程组为 .
【解答】解:设班级人数为x人,组数为y组,
由题意得:.
故答案为:.
16.(2024秋 朝阳区校级期末)如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= 50° .
【解答】解:∵∠1=40°,
∴∠3=90°﹣40°=50°,
∵直线l1∥l2,
∴∠2=∠3=50°.
故答案为:50°.
三.解答题(共10小题)
17.(2025春 吐鲁番市期末)计算:.
【解答】解:原式.
18.(2025春 上海期末)(1)解方程组:;
(2)解方程组:.
【解答】解:(1),
根据消元法可知①×2,得2y﹣6x=﹣10③,
②﹣③,得10x=21,
解得:x=2.1,
把x=2.1代入①,得y﹣6.3=﹣5,
解得y=1.3,
∴;
(2)
①+②得:8x﹣z=18④,
②+③得:6x+2z=8⑤,
联立得,
根据消元法可知④×2+⑤得:22x=44,
解得x=2,
将x=2代入④得,
解得:z=﹣2,
将x=2,z=﹣2代入③得:2+y﹣(﹣2)=3,
解得y=﹣1,
∴.
19.(2023秋 高新区校级期末)解不等式,并把不等式的解集在数轴上表示出来.
【解答】解:,
去分母,两边乘以10,得:5(3+2x)﹣10<2(1+2x),
去括号,得:15+10x﹣10<2+4x,
移项,得:10x﹣4x<2﹣15+10,
合并同类项,得:6x<﹣3,
系数化为1,得:,
不等式的解集在数轴上表示如下:
20.(2024秋 东坡区期末)解不等式组:,将其解集在数轴上表示出来,并写出所有的整数解.
【解答】解:解不等式①得x≤3,
解不等式②得x>﹣1,
所以不等式组的解集为﹣1<x≤3,
解集在数轴上表示为:
不等式组的整数解为0,1,2,3.
21.(2025春 五华区校级期末)如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)求证:∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
【解答】(1)证明:∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°
∴AD∥CE
∴∠ADC+∠3=180°
又∵∠2+∠3=180°,
∴∠2=∠ADC
∴AB∥CD
∴∠1=∠BDC
(2)解:∵AD⊥EF,
∴∠FAD=90°.
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC∠BDC70°=35°.
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD﹣∠2=90°﹣35°=55°.
22.(2024秋 西安期末)如果一个正数m的两个平方根分别是2a﹣3和a﹣9,n+2的算术平方根是1.
(1)求m和n的值.
(2)求m﹣11n的算术平方根.
【解答】解:(1)∵一个正数m的两个平方根分别是2a﹣3和a﹣9,
∴2a﹣3+a﹣9=0,
解得:a=4,
∴2a﹣3=5,
∴m=25,
∵n+2的算术平方根是1
∴n+2=1
∴n=﹣1;
(2)由(1)得m=25,n=﹣1,
∴m﹣11n=25+11=36,
∴m﹣11n的算术平方根为6.
23.(2024秋 榆树市期末)完成下面的证明:
如图,已知AB∥EF,EP⊥EQ,∠1+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE= ∠2 ( 两直线平行,内错角相等 ).
∵EP⊥EQ,
∴∠PEQ= 90° ( 垂直的定义 ).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1= ∠3 .
∴ EF ∥CD( 内错角相等,两直线平行 ).
又∵AB∥EF,
∴AB∥CD( 平行于同一直线的两条直线互相平行 ).
【解答】证明:∵AB∥EF,
∴∠APE=∠2(两直线平行,内错角相等).
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1=∠3.
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥EF,
∴AB∥CD(平行于同一直线的两条直线互相平行).
故答案为:∠2;两直线平行,内错角相等;90°;垂直的定义;∠3;EF;内错角相等,两直线平行;平行于同一直线的两条直线互相平行.
24.(2024秋 天府新区期末)天府新区体育公园已开工,根据平面规划图来看,有新建篮球场、足球场、网球场、健身步道、健身广场、儿童成长体育乐园及其他公共服务配套设施,共有12块运动场地,可开展多项体育运动.某中学决定在学生中开展跳绳、篮球、乒乓球、跑步和足球五种项目,为了解学生对五种项目的喜欢情况,随机调查了该校n名学生最喜欢的一种项目(每名学生必选且只能选择五种项目中的一种),并将调查结果绘制成如下两幅不完整的统计图:
根据统计图中提供的信息,解答下列问题:
(1)n的值为 100 ,扇形统计图中“足球”部分所对应的圆心角度数为 54° ;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计该校1500名学生中有多少名学生最喜欢乒乓球项目.
【解答】解:(1)根据题意n=25÷25%=100,360°54°,
故答案为:100,54;
(2)“篮球”人数为100×30%=30(名),
“跑步”人数为100﹣25﹣30﹣20﹣15=10(名),
补全图形如下:
(3)估计该校1500名学生中最喜欢乒乓球项目的学生有1500×20%=300(名).
答:估计该校1500名学生中最喜欢乒乓球项目的学生有300名.
25.(2024秋 长沙期末)“文房四宝”是中国独有的书法绘画工具,即笔、墨、纸、砚,文房四宝之名,起源于南北朝时期.我校为了落实双减政策,丰富学生的课后服务活动,开设了书法社团,计划为学生购买甲、乙两种型号“文房四宝”,经过调查得知:每套甲型号“文房四宝”的价格比每套乙型号的价格贵30元,买5套甲型号“文房四宝”和10套乙型号“文房四宝”共用900元.
(1)求每套甲、乙型号“文房四宝”的价格分别是多少?
(2)若学校需购进甲、乙两种型号“文房四宝”共100套,总费用不超过5870元,并且根据学生需求,要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍,请问共有几种购买方案?最低费用是多少?
【解答】解:(1)设每套甲型号“文房四宝”的价格是x元,则每套乙型号“文房四宝”的价格是(x﹣30)元,
根据题意得:5x+10(x﹣30)=900,
解得:x=80,
∴x﹣30=80﹣30=50(元).
答:每套甲型号“文房四宝”的价格是80元,每套乙型号“文房四宝”的价格是50元;
(2)设购买m套甲型号“文房四宝”,则购买(100﹣m)套乙型号“文房四宝”,
根据题意得:,
解得:25<m≤29,
∵m为正整数,
∴m可以为26,27,28,29,
∴共有4种购买方案,
方案1:购买26套甲型号“文房四宝”,74套乙型号“文房四宝”,所需费用为80×26+50×74=5780(元);
方案2:购买27套甲型号“文房四宝”,73套乙型号“文房四宝”,所需费用为80×27+50×73=5810(元);
方案3:购买28套甲型号“文房四宝”,72套乙型号“文房四宝”,所需费用为80×28+50×72=5840(元);
方案4:购买29套甲型号“文房四宝”,71套乙型号“文房四宝”,所需费用为80×29+50×71=5870(元),
∵5780<5810<5840<5870,
∴最低费用为5780元.
答:共有4种购买方案,最低费用为5780元.
26.(2024秋 沈阳期末)【发现问题】
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
【提出问题】
小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ∠AMP=∠P+∠CNP ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= 145 °(不需要写解答过程)
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.
【解答】解:探究一:∠BPD=∠ABP+∠CDP,理由如下:
如图①,
∵AB∥MN∥CD,
∴∠BPN=∠ABP,∠DPN=∠CDP,
∴∠BPN+∠DPN=∠ABP+∠CDP,
∴∠BPD=∠ABP+∠CDP.
探究二:如图②,
∠AMP=∠P+∠CNP,理由如下:
∵AB∥CD,
∴∠MKP=∠CNP,
∵∠AMP=∠P+∠MKP,
∴∠AMP=∠P+∠CNP.
如图③,延长EA交BC于L,
∵AE∥CD,
∴∠ALC=∠C=60°,
∴∠ALB=180°﹣∠ALC=120°,
∴∠BAE=∠B+∠ALB=25°+120°=145°.
故答案为:∠AMP=∠P+∠CNP,145.
∵射线ME,NF分别平分∠BMP和∠CNP,
∴∠PME∠PMB,∠CNF=∠PNF,
如图④,
由探究一的结论得:∠P=∠AMF+∠PMF+∠CNF+∠PNF,∠F=∠AMF+∠CNF,
∵∠P=2∠F,
∴∠AMF+∠PMF+∠CNF+∠PNF=2∠AMF+2∠CNF,
∵∠CNF=∠PNF,
∴∠AMF+∠PMF=2∠AMF,
∴∠PMF=∠AMF∠AMP,
∴∠PMF+∠PME(∠AMP+∠PMB),
∴∠FME∠AMB180°=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
一.选择题(共8小题)
1.(2024春 余干县校级期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
2.(2024春 七星关区校级期末)一把直尺和一个含30°角的直角三角板按如图方式放置,若∠1=25°,则∠2=( )
A.25° B.30° C.35° D.45°
3.(2022秋 江北区校级期末)如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
4.(2025春 五华区校级期末)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOB=45°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
5.(2024秋 长安区期末)“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则2x+y的值为( )
A.﹣5 B.﹣4 C.4 D.5
6.(2025春 上海期末)在下列方程组中,属于二元一次方程组的是( )
A. B.
C. D.
7.(2025春 五华区校级期末)如果点A(m﹣8,m﹣2)在x轴上,那么点B(m+1,m﹣6)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8.(2025春 隆昌市校级期末)关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
二.填空题(共8小题)
9.(2024春 硚口区期末)写出一个小于3的正无理数 .
10.(2021秋 开化县期末)不等式3x﹣1<5的解集为 .
11.(2024春 张店区期末)比较大小:2 (填“>”、“<”或“=”).
12.(2025春 五华区校级期末)为了估计学校池塘中鱼的数量,九年级一班的同学采用如下方法:从池塘中捕上50条鱼做上标记,然后放回池塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再捕上50条,若其中带有标记的鱼有10条,则池塘中鱼估计有 条.
13.(2025春 虹口区校级期末)关于x,y的方程组有无数组解,则ab= .
14.(2025春 五华区校级期末)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为 .
15.(2025春 上海期末)某班级同学分组,若每组5人则余3人,若每组6人则缺5人.设班级人数为x人,组数为y组,则列方程组为 .
16.(2024秋 朝阳区校级期末)如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= .
三.解答题(共10小题)
17.(2025春 吐鲁番市期末)计算:.
18.(2025春 上海期末)(1)解方程组:;
(2)解方程组:.
19.(2023秋 高新区校级期末)解不等式,并把不等式的解集在数轴上表示出来.
20.(2024秋 东坡区期末)解不等式组:,将其解集在数轴上表示出来,并写出所有的整数解.
21.(2025春 五华区校级期末)如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)求证:∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
22.(2024秋 西安期末)如果一个正数m的两个平方根分别是2a﹣3和a﹣9,n+2的算术平方根是1.
(1)求m和n的值.
(2)求m﹣11n的算术平方根.
23.(2024秋 榆树市期末)完成下面的证明:
如图,已知AB∥EF,EP⊥EQ,∠1+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE= ( ).
∵EP⊥EQ,
∴∠PEQ= ( ).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1= .
∴ ∥CD( ).
又∵AB∥EF,
∴AB∥CD( ).
24.(2024秋 天府新区期末)天府新区体育公园已开工,根据平面规划图来看,有新建篮球场、足球场、网球场、健身步道、健身广场、儿童成长体育乐园及其他公共服务配套设施,共有12块运动场地,可开展多项体育运动.某中学决定在学生中开展跳绳、篮球、乒乓球、跑步和足球五种项目,为了解学生对五种项目的喜欢情况,随机调查了该校n名学生最喜欢的一种项目(每名学生必选且只能选择五种项目中的一种),并将调查结果绘制成如下两幅不完整的统计图:
根据统计图中提供的信息,解答下列问题:
(1)n的值为 ,扇形统计图中“足球”部分所对应的圆心角度数为 ;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计该校1500名学生中有多少名学生最喜欢乒乓球项目.
25.(2024秋 长沙期末)“文房四宝”是中国独有的书法绘画工具,即笔、墨、纸、砚,文房四宝之名,起源于南北朝时期.我校为了落实双减政策,丰富学生的课后服务活动,开设了书法社团,计划为学生购买甲、乙两种型号“文房四宝”,经过调查得知:每套甲型号“文房四宝”的价格比每套乙型号的价格贵30元,买5套甲型号“文房四宝”和10套乙型号“文房四宝”共用900元.
(1)求每套甲、乙型号“文房四宝”的价格分别是多少?
(2)若学校需购进甲、乙两种型号“文房四宝”共100套,总费用不超过5870元,并且根据学生需求,要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍,请问共有几种购买方案?最低费用是多少?
26.(2024秋 沈阳期末)【发现问题】
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
【提出问题】
小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= °(不需要写解答过程)
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.
期末真题重组练习卷-2024-2025学年数学七年级下册人教版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B C C C B C D B
一.选择题(共8小题)
1.(2024春 余干县校级期末)估计的值在( )
A.1和2之间 B.2和3之间 C.3和4之间 D.4和5之间
【解答】解:∵,3,
而,
∴2,
∴估计的值在2和3之间.
故选:B.
2.(2024春 七星关区校级期末)一把直尺和一个含30°角的直角三角板按如图方式放置,若∠1=25°,则∠2=( )
A.25° B.30° C.35° D.45°
【解答】解:如图,
∵AB∥CD,
∴∠1=∠ABC=25°,
∵∠MBC=60°,
∴∠2=∠MBC﹣∠ABC=35°,
故选:C.
3.(2022秋 江北区校级期末)如图,已知OP平分∠AOB,∠AOB=30°,PC∥OA,则∠CPO为( )
A.30° B.10° C.15° D.5°
【解答】解:∵OP是∠AOB的平分线,∠AOB=30°,
∴∠POA∠AOB=15°,
∵PC∥OA,
∴∠CPO=∠POA=15°.
故选:C.
4.(2025春 五华区校级期末)已知直线AB,CD相交于点O,如图所示,OE⊥AB于点O,若∠DOB=45°,则∠COE的度数是( )
A.25° B.35° C.45° D.55°
【解答】解:∵直线AB,CD相交于点O,∠DOB=45°,
∴∠AOC=∠DOB=45°,
∵OE⊥AB,
∴∠AOE=90°,
∴∠COE=∠AOE﹣∠AOC=90°﹣45°=45°.
故选:C.
5.(2024秋 长安区期末)“九宫图”传说是远古时代洛河中的一个神龟背上的图案,故又称“龟背图”,中国古代数学史上经常研究这一神话.数学上的“九宫图”所体现的是一个3×3表格,其每行、每列、每条对角线上三个数字之和都相等,也称为三阶幻方,如图是一个三阶幻方,则2x+y的值为( )
A.﹣5 B.﹣4 C.4 D.5
【解答】解:由题意得:,
解得:,
∴2x+y=2×(﹣3)+2=﹣4,
故选:B.
6.(2025春 上海期末)在下列方程组中,属于二元一次方程组的是( )
A. B.
C. D.
【解答】解:A、是三元一次方程组,故选项不符合题意;
B、是二元二次方程组,故选项不符合题意;
C、是二元一次方程组,故选项符合题意;
D、是分式方程组,故选项不符合题意;
故选:C.
7.(2025春 五华区校级期末)如果点A(m﹣8,m﹣2)在x轴上,那么点B(m+1,m﹣6)所在的象限是( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【解答】解:由题意得,m﹣2=0,
解得,m=2,
∴m+1=3,m﹣6=﹣4,
∴B(m+1,m﹣6)在第四象限.
故选:D.
8.(2025春 隆昌市校级期末)关于y的一元一次不等式组有3个整数解,则a的取值范围是( )
A.a≤2 B.1<a≤2 C.a≥1 D.1≤a<2
【解答】解:,
由①得:y>﹣2,
由②得:y<a,
∴原不等式组的解集为﹣2<y<a,
∵关于y的一元一次不等式组有3个整数解,
∴1<a≤2,
故选:B.
二.填空题(共8小题)
9.(2024春 硚口区期末)写出一个小于3的正无理数 (答案不唯一) .
【解答】解:本题答案不唯一:如等.
故答案为:(答案不唯一).
10.(2021秋 开化县期末)不等式3x﹣1<5的解集为 x<2 .
【解答】解:3x﹣1<5,
3x<6,
x<2.
故答案为:x<2.
11.(2024春 张店区期末)比较大小:2 < (填“>”、“<”或“=”).
【解答】解:∵2,
∴,
∴2;
故答案为:<.
12.(2025春 五华区校级期末)为了估计学校池塘中鱼的数量,九年级一班的同学采用如下方法:从池塘中捕上50条鱼做上标记,然后放回池塘.经过一段时间,待有标记的鱼完全混合于鱼群后,再捕上50条,若其中带有标记的鱼有10条,则池塘中鱼估计有 250 条.
【解答】解:池塘中鱼估计有:50250(条),
故答案为:250.
13.(2025春 虹口区校级期末)关于x,y的方程组有无数组解,则ab= .
【解答】解:因为关于x,y的方程组有无数组解,
设比例系数k,
所以,﹣1=3bk,1=2k,
解得:,a=1,b,
所以ab.
故答案为:.
14.(2025春 五华区校级期末)如图,两个完全一样的直角三角形重叠在一起,将其中的一个三角形沿着B到点C的方向平移到△DEF的位置,AB=10,EH=7,平移距离是6,则图中阴影部分的面积为 51 .
【解答】解:∵S△ABC=S△DEF,
∴S阴=S梯形ABEH (10+7)×6=51
故答案为:51.
15.(2025春 上海期末)某班级同学分组,若每组5人则余3人,若每组6人则缺5人.设班级人数为x人,组数为y组,则列方程组为 .
【解答】解:设班级人数为x人,组数为y组,
由题意得:.
故答案为:.
16.(2024秋 朝阳区校级期末)如图,直线l1∥l2,将直角三角板按如图方式放置,直角顶点在l2上,若∠1=40°,则∠2= 50° .
【解答】解:∵∠1=40°,
∴∠3=90°﹣40°=50°,
∵直线l1∥l2,
∴∠2=∠3=50°.
故答案为:50°.
三.解答题(共10小题)
17.(2025春 吐鲁番市期末)计算:.
【解答】解:原式.
18.(2025春 上海期末)(1)解方程组:;
(2)解方程组:.
【解答】解:(1),
根据消元法可知①×2,得2y﹣6x=﹣10③,
②﹣③,得10x=21,
解得:x=2.1,
把x=2.1代入①,得y﹣6.3=﹣5,
解得y=1.3,
∴;
(2)
①+②得:8x﹣z=18④,
②+③得:6x+2z=8⑤,
联立得,
根据消元法可知④×2+⑤得:22x=44,
解得x=2,
将x=2代入④得,
解得:z=﹣2,
将x=2,z=﹣2代入③得:2+y﹣(﹣2)=3,
解得y=﹣1,
∴.
19.(2023秋 高新区校级期末)解不等式,并把不等式的解集在数轴上表示出来.
【解答】解:,
去分母,两边乘以10,得:5(3+2x)﹣10<2(1+2x),
去括号,得:15+10x﹣10<2+4x,
移项,得:10x﹣4x<2﹣15+10,
合并同类项,得:6x<﹣3,
系数化为1,得:,
不等式的解集在数轴上表示如下:
20.(2024秋 东坡区期末)解不等式组:,将其解集在数轴上表示出来,并写出所有的整数解.
【解答】解:解不等式①得x≤3,
解不等式②得x>﹣1,
所以不等式组的解集为﹣1<x≤3,
解集在数轴上表示为:
不等式组的整数解为0,1,2,3.
21.(2025春 五华区校级期末)如图,已知AD⊥EF,CE⊥EF,∠2+∠3=180°.
(1)求证:∠1=∠BDC;
(2)若∠1=70°,DA平分∠BDC,试求∠FAB的度数.
【解答】(1)证明:∵AD⊥EF,CE⊥EF,
∴∠GAD=∠GEC=90°
∴AD∥CE
∴∠ADC+∠3=180°
又∵∠2+∠3=180°,
∴∠2=∠ADC
∴AB∥CD
∴∠1=∠BDC
(2)解:∵AD⊥EF,
∴∠FAD=90°.
∵AB∥CD,
∴∠BDC=∠1=70°,
∵DA平分∠BDC,
∴∠ADC∠BDC70°=35°.
∵AB∥CD,
∴∠2=∠ADC=35°,
∴∠FAB=∠FAD﹣∠2=90°﹣35°=55°.
22.(2024秋 西安期末)如果一个正数m的两个平方根分别是2a﹣3和a﹣9,n+2的算术平方根是1.
(1)求m和n的值.
(2)求m﹣11n的算术平方根.
【解答】解:(1)∵一个正数m的两个平方根分别是2a﹣3和a﹣9,
∴2a﹣3+a﹣9=0,
解得:a=4,
∴2a﹣3=5,
∴m=25,
∵n+2的算术平方根是1
∴n+2=1
∴n=﹣1;
(2)由(1)得m=25,n=﹣1,
∴m﹣11n=25+11=36,
∴m﹣11n的算术平方根为6.
23.(2024秋 榆树市期末)完成下面的证明:
如图,已知AB∥EF,EP⊥EQ,∠1+∠APE=90°,求证:AB∥CD.
证明:∵AB∥EF,
∴∠APE= ∠2 ( 两直线平行,内错角相等 ).
∵EP⊥EQ,
∴∠PEQ= 90° ( 垂直的定义 ).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1= ∠3 .
∴ EF ∥CD( 内错角相等,两直线平行 ).
又∵AB∥EF,
∴AB∥CD( 平行于同一直线的两条直线互相平行 ).
【解答】证明:∵AB∥EF,
∴∠APE=∠2(两直线平行,内错角相等).
∵EP⊥EQ,
∴∠PEQ=90°(垂直的定义).
即∠2+∠3=90°.
∴∠APE+∠3=90°.
∵∠1+∠APE=90°,
∴∠1=∠3.
∴EF∥CD(内错角相等,两直线平行).
又∵AB∥EF,
∴AB∥CD(平行于同一直线的两条直线互相平行).
故答案为:∠2;两直线平行,内错角相等;90°;垂直的定义;∠3;EF;内错角相等,两直线平行;平行于同一直线的两条直线互相平行.
24.(2024秋 天府新区期末)天府新区体育公园已开工,根据平面规划图来看,有新建篮球场、足球场、网球场、健身步道、健身广场、儿童成长体育乐园及其他公共服务配套设施,共有12块运动场地,可开展多项体育运动.某中学决定在学生中开展跳绳、篮球、乒乓球、跑步和足球五种项目,为了解学生对五种项目的喜欢情况,随机调查了该校n名学生最喜欢的一种项目(每名学生必选且只能选择五种项目中的一种),并将调查结果绘制成如下两幅不完整的统计图:
根据统计图中提供的信息,解答下列问题:
(1)n的值为 100 ,扇形统计图中“足球”部分所对应的圆心角度数为 54° ;
(2)请根据以上信息直接在答题卡中补全条形统计图;
(3)根据抽样调查结果,请你估计该校1500名学生中有多少名学生最喜欢乒乓球项目.
【解答】解:(1)根据题意n=25÷25%=100,360°54°,
故答案为:100,54;
(2)“篮球”人数为100×30%=30(名),
“跑步”人数为100﹣25﹣30﹣20﹣15=10(名),
补全图形如下:
(3)估计该校1500名学生中最喜欢乒乓球项目的学生有1500×20%=300(名).
答:估计该校1500名学生中最喜欢乒乓球项目的学生有300名.
25.(2024秋 长沙期末)“文房四宝”是中国独有的书法绘画工具,即笔、墨、纸、砚,文房四宝之名,起源于南北朝时期.我校为了落实双减政策,丰富学生的课后服务活动,开设了书法社团,计划为学生购买甲、乙两种型号“文房四宝”,经过调查得知:每套甲型号“文房四宝”的价格比每套乙型号的价格贵30元,买5套甲型号“文房四宝”和10套乙型号“文房四宝”共用900元.
(1)求每套甲、乙型号“文房四宝”的价格分别是多少?
(2)若学校需购进甲、乙两种型号“文房四宝”共100套,总费用不超过5870元,并且根据学生需求,要求购进乙型号“文房四宝”的数量必须低于甲型号“文房四宝”数量的3倍,请问共有几种购买方案?最低费用是多少?
【解答】解:(1)设每套甲型号“文房四宝”的价格是x元,则每套乙型号“文房四宝”的价格是(x﹣30)元,
根据题意得:5x+10(x﹣30)=900,
解得:x=80,
∴x﹣30=80﹣30=50(元).
答:每套甲型号“文房四宝”的价格是80元,每套乙型号“文房四宝”的价格是50元;
(2)设购买m套甲型号“文房四宝”,则购买(100﹣m)套乙型号“文房四宝”,
根据题意得:,
解得:25<m≤29,
∵m为正整数,
∴m可以为26,27,28,29,
∴共有4种购买方案,
方案1:购买26套甲型号“文房四宝”,74套乙型号“文房四宝”,所需费用为80×26+50×74=5780(元);
方案2:购买27套甲型号“文房四宝”,73套乙型号“文房四宝”,所需费用为80×27+50×73=5810(元);
方案3:购买28套甲型号“文房四宝”,72套乙型号“文房四宝”,所需费用为80×28+50×72=5840(元);
方案4:购买29套甲型号“文房四宝”,71套乙型号“文房四宝”,所需费用为80×29+50×71=5870(元),
∵5780<5810<5840<5870,
∴最低费用为5780元.
答:共有4种购买方案,最低费用为5780元.
26.(2024秋 沈阳期末)【发现问题】
如图①,小明同学在做光的折射实验时发现:平行于主光轴MN的光线AB和CD经过凹透镜的折射后,折射光线BE,DF的反向延长线交于主光轴MN上一点P.
【提出问题】
小明提出:∠BPD,∠ABP和∠CDP三个角之间存在着怎样的数量关系?
【分析问题】
已知平行,可以利用平行线的性质,把∠BPD分成两部分进行研究.
【解决问题】
探究一:请你帮小明解决这个问题,并说明理由.
探究二:如图②,∠P,∠AMP,∠CNP的数量关系为 ∠AMP=∠P+∠CNP ;如图③,已知∠ABC=25°,∠C=60°,AE∥CD,则∠BAE= 145 °(不需要写解答过程)
利用探究一得到的结论解决下列问题:
如图④,射线ME,NF分别平分∠BMP和∠CNP,ME交直线CD于点E,NF与∠AMP内部的一条射线MF交于点F,若∠P=2∠F,求∠FME的度数.
【解答】解:探究一:∠BPD=∠ABP+∠CDP,理由如下:
如图①,
∵AB∥MN∥CD,
∴∠BPN=∠ABP,∠DPN=∠CDP,
∴∠BPN+∠DPN=∠ABP+∠CDP,
∴∠BPD=∠ABP+∠CDP.
探究二:如图②,
∠AMP=∠P+∠CNP,理由如下:
∵AB∥CD,
∴∠MKP=∠CNP,
∵∠AMP=∠P+∠MKP,
∴∠AMP=∠P+∠CNP.
如图③,延长EA交BC于L,
∵AE∥CD,
∴∠ALC=∠C=60°,
∴∠ALB=180°﹣∠ALC=120°,
∴∠BAE=∠B+∠ALB=25°+120°=145°.
故答案为:∠AMP=∠P+∠CNP,145.
∵射线ME,NF分别平分∠BMP和∠CNP,
∴∠PME∠PMB,∠CNF=∠PNF,
如图④,
由探究一的结论得:∠P=∠AMF+∠PMF+∠CNF+∠PNF,∠F=∠AMF+∠CNF,
∵∠P=2∠F,
∴∠AMF+∠PMF+∠CNF+∠PNF=2∠AMF+2∠CNF,
∵∠CNF=∠PNF,
∴∠AMF+∠PMF=2∠AMF,
∴∠PMF=∠AMF∠AMP,
∴∠PMF+∠PME(∠AMP+∠PMB),
∴∠FME∠AMB180°=90°.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
