期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)(含详解)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 607.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:46:30 | ||
图片预览



文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2025春 五华区校级期末)已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为( )
A.3 B.4 C.5 D.6
2.(2015春 平顶山期末)下列计算正确的是( )
A.a3+a2=a5 B.a3 a2=a6 C.(a3)2=a9 D.a6÷a2=a4
3.(2024秋 丹巴县期末)若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
4.(2025春 河西区校级期末)《九章算术 盈不足》载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二.问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出11钱,就多了8钱:如果每人出9钱,就少了12钱.问一共有多少人?这个物品的价格是多少?设共有x人,物品的价格为y钱,则可列方程组为( )
A. B.
C. D.
5.(2022春 玉林期末)小华去商店购买A、B两种玩具,共用了12元,A种玩具每件1元,B种玩具每件3元.若每种玩具至少买一件,且A种玩具的数量不少于B种玩具的数量,则小华的购买方案有( )
A.7种 B.6种 C.4种 D.3种
6.(2024春 西青区期末)下列命题中真命题是( )
A.互为相反数的两个数和为0
B.相等的角是对顶角
C.若两个角的和为180°,则这两个角互为邻补角
D.同位角相等
7.(2025春 徐州期末)下列各式不能使用平方差公式的是( )
A.(2a+b)(2a﹣b) B.(2a﹣b)(b﹣2a)
C.(﹣2a+b)(﹣2a﹣b) D.(2a﹣b)(﹣2a﹣b)
8.(2024春 谷城县期末)若关于x的不等式组的解集为x<3,则m的取值范围是( )
A.m>2 B.m≥2 C.m<2 D.m≤2
二.填空题(共8小题)
9.(2025春 成都校级期末)已知27a=81b+1,则9a2﹣16b2﹣32b的值为 .
10.(2021春 顺义区期末)写出一个以为解的二元一次方程 .
11.(2024春 盱眙县期末)不等式2x+3>1的解集为 .
12.(2023秋 蜀山区期末)写出“对顶角相等”的逆命题 .
13.(2024秋 康平县期末)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为 .
14.(2022秋 玉林期末)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为 .
15.(2021春 固始县期末)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
16.(2025春 隆昌市校级期末)已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是 .
三.解答题(共7小题)
17.(2024秋 深圳校级期末)解下列方程组:
(1);
(2).
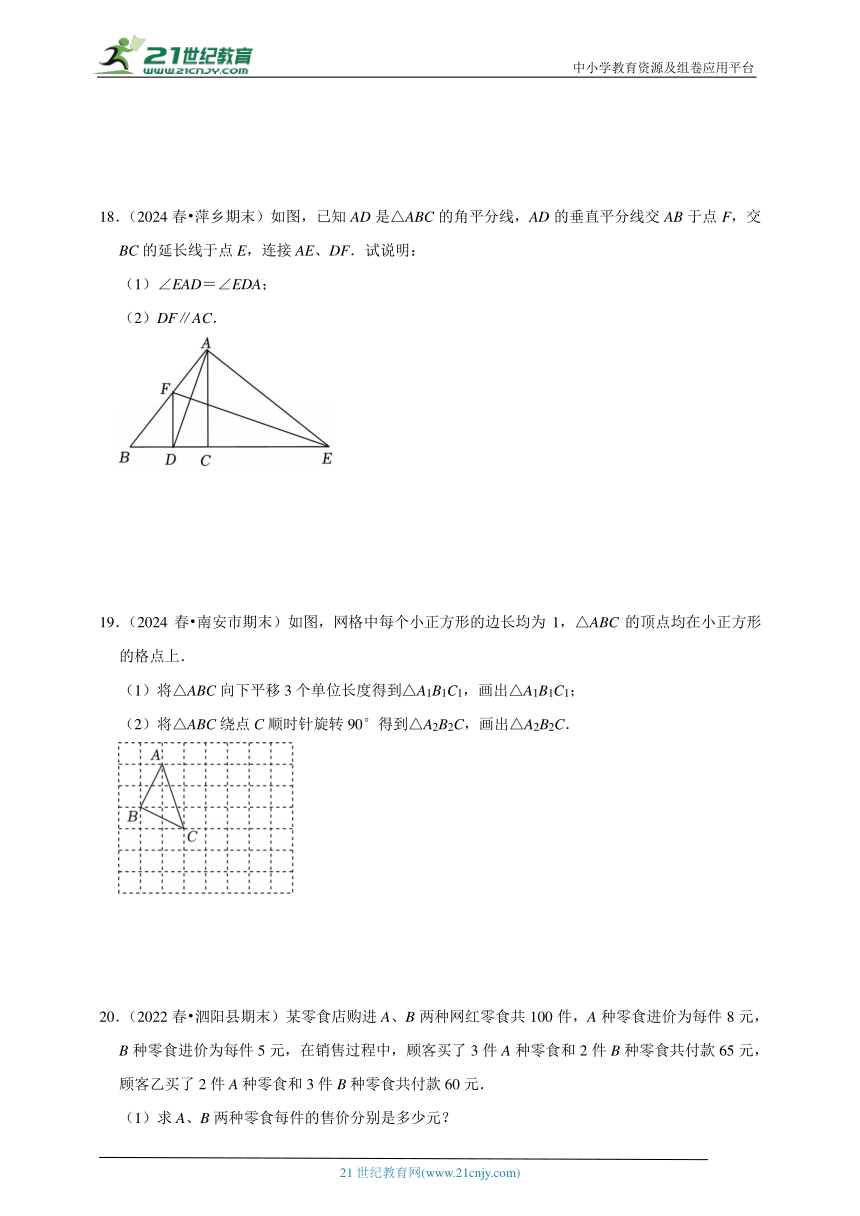
18.(2024春 萍乡期末)如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
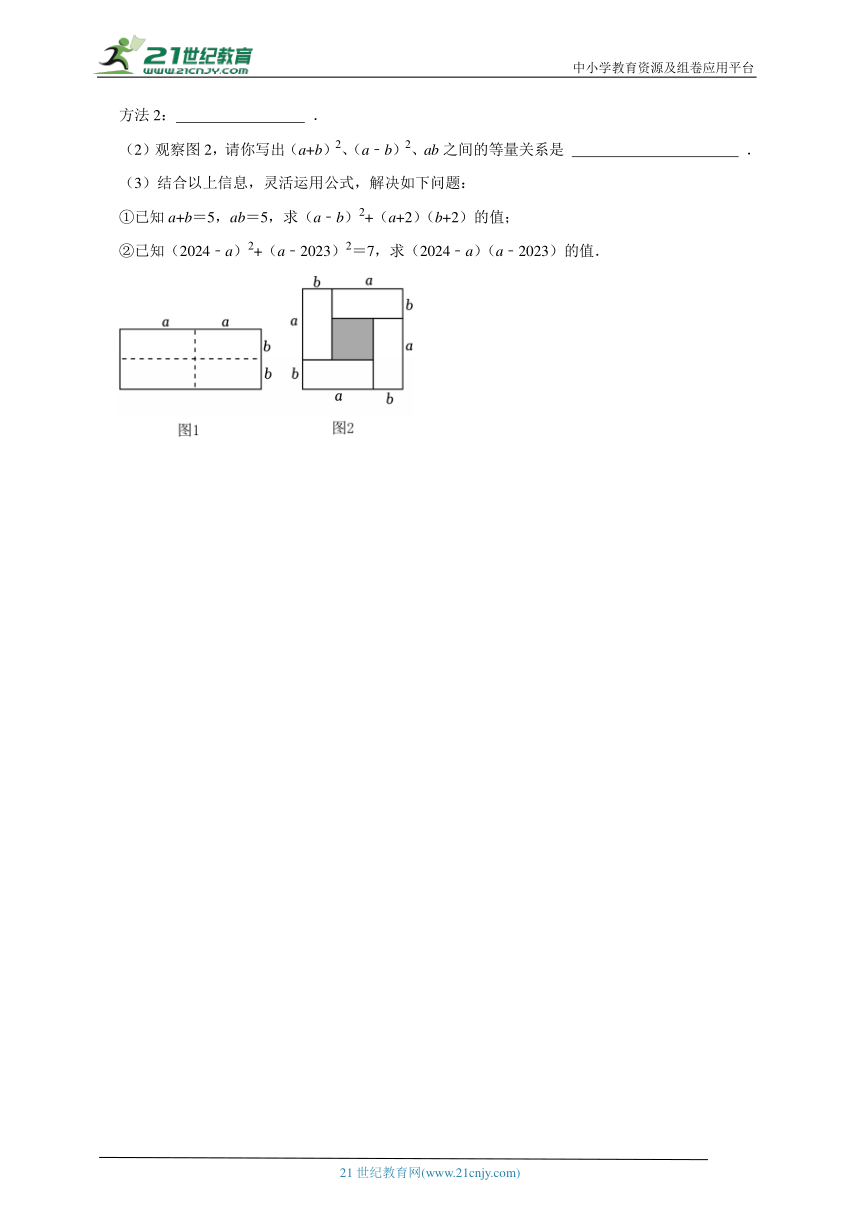
19.(2024春 南安市期末)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C,画出△A2B2C.
20.(2022春 泗阳县期末)某零食店购进A、B两种网红零食共100件,A种零食进价为每件8元,B种零食进价为每件5元,在销售过程中,顾客买了3件A种零食和2件B种零食共付款65元,顾客乙买了2件A种零食和3件B种零食共付款60元.
(1)求A、B两种零食每件的售价分别是多少元?
(2)若该零食店计划A、B两种零食的进货总投入不超过656元,且销售完后总利润不低于600元,则购进A、B两种零食有多少种进货方案?
(3)在(2)的条件下,哪种进货方案可使获利最大?最大利润是多少元?
21.(2024春 和县期末)阅读材料:如果x是一个有理数,我们把不超过x的最大整数记作[x].
例如,[3.2]=3,[5]=5,[﹣2.1]=﹣3.
那么,x=[x]+a,其中0≤a<1.
例如,3.2=[3.2]+0.2,5=[5]+0.﹣2.1=[﹣2.1]+0.9.请你解决下列问题:
(1)[4.8]= ,[﹣6.5]= ,[0]= :
(2)如果[x]=3,那么x的取值范围是 ;
(3)如果[5x﹣2]=3x+1,求x的值.
22.(2024春 惠城区校级期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为x>﹣1,请求常数“□”的取值范围.
23.(2024春 贵州期末)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.数学活动课上,老师展示了如图1的长方形纸片,它是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的形状拼成一个正方形,请解答下列问题:
(1)请用两种不同的方法表示图2中阴影部分的面积:
方法1: ;
方法2: .
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)结合以上信息,灵活运用公式,解决如下问题:
①已知a+b=5,ab=5,求(a﹣b)2+(a+2)(b+2)的值;
②已知(2024﹣a)2+(a﹣2023)2=7,求(2024﹣a)(a﹣2023)的值.
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B D C C D A B B
一.选择题(共8小题)
1.(2025春 五华区校级期末)已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为( )
A.3 B.4 C.5 D.6
【解答】解:∵(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,
∴m+4≠0且|m|﹣3=1,
∴m≠﹣4且m=±4,
∴m=4,
故选:B.
2.(2015春 平顶山期末)下列计算正确的是( )
A.a3+a2=a5 B.a3 a2=a6 C.(a3)2=a9 D.a6÷a2=a4
【解答】解:A、a3+a2不是同类项,不能合并,错误;
B、a3 a2=a5,错误;
C、(a3)2=a6,错误;
D、a6÷a2=a4,正确;
故选:D.
3.(2024秋 丹巴县期末)若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
【解答】解:把代入方程3x+ay=1得:
﹣3+2a=1,
∴a=2.
故选:C.
4.(2025春 河西区校级期末)《九章算术 盈不足》载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二.问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出11钱,就多了8钱:如果每人出9钱,就少了12钱.问一共有多少人?这个物品的价格是多少?设共有x人,物品的价格为y钱,则可列方程组为( )
A. B.
C. D.
【解答】解:设共有x人,物品的价格为y钱,根据题意得:
.
故选:C.
5.(2022春 玉林期末)小华去商店购买A、B两种玩具,共用了12元,A种玩具每件1元,B种玩具每件3元.若每种玩具至少买一件,且A种玩具的数量不少于B种玩具的数量,则小华的购买方案有( )
A.7种 B.6种 C.4种 D.3种
【解答】解:设小华购买了A种玩具x件,则购买的B种玩具为件,根据题意得,
,
解得,3≤x≤9,
∵x为整数,也为整数,
∴x=3或6或9,
∴有3种购买方案.
故选:D.
6.(2024春 西青区期末)下列命题中真命题是( )
A.互为相反数的两个数和为0
B.相等的角是对顶角
C.若两个角的和为180°,则这两个角互为邻补角
D.同位角相等
【解答】解:A、互为相反数的两个数和为0,原命题正确,故A选项符合题意;
B、相等的角不一定是对顶角,原命题错误,故B选项不符合题意;
C、若两个角的和为180°,则这两个角互补,不一定是邻补角,原命题错误,故C选项不符合题意;
D、两直线平行,同位角相等,原命题错误,故D选项不符合题意.
故选:A.
7.(2025春 徐州期末)下列各式不能使用平方差公式的是( )
A.(2a+b)(2a﹣b) B.(2a﹣b)(b﹣2a)
C.(﹣2a+b)(﹣2a﹣b) D.(2a﹣b)(﹣2a﹣b)
【解答】解:各式不能使用平方差公式的是(2a﹣b)(b﹣2a),
故选:B.
8.(2024春 谷城县期末)若关于x的不等式组的解集为x<3,则m的取值范围是( )
A.m>2 B.m≥2 C.m<2 D.m≤2
【解答】解:解不等式2x﹣1<5,得:x<3,
∵关于x的不等式组的解集为x<3,
∴m+1≥3,
∴m≥2.
故选:B.
二.填空题(共8小题)
9.(2025春 成都校级期末)已知27a=81b+1,则9a2﹣16b2﹣32b的值为 16 .
【解答】解:∵27a=81b+1,
∴(33)a=(34)b+1,
∴33a=34b+4,
∴3a=4b+4,
∴3a﹣4b=4,
∴9a2﹣16b2﹣32b
=(3a﹣4b)(3a+4b)﹣32b
=4(3a+4b)﹣32b
=12a+16b﹣32b
=12a﹣16b
=4(3a﹣4b)
=4×4
=16,
故答案为:16.
10.(2021春 顺义区期末)写出一个以为解的二元一次方程 2x﹣y=1 .
【解答】解:答案不唯一,如2x﹣y=1.
故答案为:2x﹣y=1.
11.(2024春 盱眙县期末)不等式2x+3>1的解集为 x>﹣1 .
【解答】解:移项,得:2x>1﹣3,
合并同类项,得:2x>﹣2,
系数化为1,得:x>﹣1,
故答案为:x>﹣1.
12.(2023秋 蜀山区期末)写出“对顶角相等”的逆命题 相等的角是对顶角 .
【解答】解:∵原命题的条件是:如果两个角是对顶角,结论是:那么这两个角相等;
∴其逆命题应该为:如两个角相等那么这两个角是对顶角,简化后即为:相等的角是对顶角.
13.(2024秋 康平县期末)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为 36 .
【解答】解:设小长方形的长为x,宽为y,则小正方形的边长为2y,
依题意得:,
解得:,
∴图中阴影部分的面积为(2y)2=(2×3)2=36.
故答案为:36.
14.(2022秋 玉林期末)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为 .
【解答】解:设大马有x匹,小马有y匹,由题意得:
,
故答案为:.
15.(2021春 固始县期末)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= 105°
【解答】解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180°﹣75°=105°.
故答案为:105°.
16.(2025春 隆昌市校级期末)已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是 .
【解答】解:设,
可得,
解得:,
故答案为:.
三.解答题(共7小题)
17.(2024秋 深圳校级期末)解下列方程组:
(1);
(2).
【解答】解:(1),
①代入②,可得:3(y+1)﹣4y=﹣2,
解得y=5,
把y=5代入①,解得x=5+1=6,
∴原方程组的解是.
(2),
由①,可得3x﹣2y=8③,
②+③,可得6x=18,
解得x=3,
把x=3代入②,可得:3×3+2y=10,
解得y=0.5,
∴原方程组的解是.
18.(2024春 萍乡期末)如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
【解答】证明:(1)∵EF是AD的垂直平分线,
∴EA=ED,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴FA=FD,
∴∠FDA=∠FAD,
∵AD平分∠BAC,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF∥AC.
19.(2024春 南安市期末)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C,画出△A2B2C.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C即为所求.
20.(2022春 泗阳县期末)某零食店购进A、B两种网红零食共100件,A种零食进价为每件8元,B种零食进价为每件5元,在销售过程中,顾客买了3件A种零食和2件B种零食共付款65元,顾客乙买了2件A种零食和3件B种零食共付款60元.
(1)求A、B两种零食每件的售价分别是多少元?
(2)若该零食店计划A、B两种零食的进货总投入不超过656元,且销售完后总利润不低于600元,则购进A、B两种零食有多少种进货方案?
(3)在(2)的条件下,哪种进货方案可使获利最大?最大利润是多少元?
【解答】解:(1)设A种零食每件的售价是x元,B种零食每件的售价是y元,
根据题意得:,
解得,
答:A种零食每件的售价是15元,B种零食每件的售价是10元;
(2)设购进A种零食m件,则购进B种零食(100﹣m)件,
∵进货总投入不超过656元,且销售完后总利润不低于600元,
∴,
解得50≤m≤52,
∵m为整数,
∴m可取50,51,52,
∴购进A、B两种零食有3种进货方案:
①购进A种零食50件,购进B种零食50件;
②购进A种零食51件,购进B种零食49件;
③购进A种零食52件,购进B种零食48件;
(3)设获利w元,
购进A种零食50件,购进B种零食50件,w=(15﹣8)×50+(10﹣5)×50=600(元),
购进A种零食51件,购进B种零食49件,w=(15﹣8)×51+(10﹣5)×49=602(元),
购进A种零食52件,购进B种零食48件,w=(15﹣8)×52+(10﹣5)×48=604(元),
∵600<602<604,
∴购进A种零食52件,购进B种零食48件,获利最大,最大利润是604元.
21.(2024春 和县期末)阅读材料:如果x是一个有理数,我们把不超过x的最大整数记作[x].
例如,[3.2]=3,[5]=5,[﹣2.1]=﹣3.
那么,x=[x]+a,其中0≤a<1.
例如,3.2=[3.2]+0.2,5=[5]+0.﹣2.1=[﹣2.1]+0.9.请你解决下列问题:
(1)[4.8]= 4 ,[﹣6.5]= ﹣7 ,[0]= 0 :
(2)如果[x]=3,那么x的取值范围是 3≤x<4 ;
(3)如果[5x﹣2]=3x+1,求x的值.
【解答】解:(1)[4.8]=4,[﹣6.5]=﹣7,[0]=0,
故答案为:4,﹣7,0;
(2)如果[x]=3,那么x的取值范围是3≤x<4,
故答案为:3≤x<4;
(3)∵[5x﹣2]=3x+1,
∴3x+1≤5x﹣2<3x+2.
解得x<2,
∵3x+1是整数,
∴x.
22.(2024春 惠城区校级期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为x>﹣1,请求常数“□”的取值范围.
【解答】解:(1),
解不等式2x﹣4<3(x﹣1)得,
∴2x﹣4<3x﹣3,
∴x>﹣1,
解不等式得,
∴2x﹣6>x﹣4,
∴x>2,
∴不等式组的解集为x>2;
(2),
设常数“□”为m,
∵,
∴2x﹣2m>x﹣4,
∴x>2m﹣4,
∴不等式的解集为x>2m﹣4,
又∵不等式2x﹣4<3(x﹣1)的解集为x>﹣1,
而不等式组的解集为x>﹣1,
∴﹣1≥2m﹣4,
∴,
∴.
23.(2024春 贵州期末)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.数学活动课上,老师展示了如图1的长方形纸片,它是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的形状拼成一个正方形,请解答下列问题:
(1)请用两种不同的方法表示图2中阴影部分的面积:
方法1: (a﹣b)2 ;
方法2: (a+b)2﹣4ab .
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 (a﹣b)2=(a+b)2﹣4ab .
(3)结合以上信息,灵活运用公式,解决如下问题:
①已知a+b=5,ab=5,求(a﹣b)2+(a+2)(b+2)的值;
②已知(2024﹣a)2+(a﹣2023)2=7,求(2024﹣a)(a﹣2023)的值.
【解答】解:(1)方法一:阴影部分是边长为a﹣b的正方形,因此面积为(a﹣b)2,
方法二:阴影部分的面积可以看作从边长为a+b的正方形面积减去4个长a,宽为b的长方形面积,即(a+b)2﹣4ab;
故答案为:(a﹣b)2,(a+b)2﹣4ab;
(2)由(1)得,(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(3)①∵a+b=5,ab=5,
∴(a﹣b)2+(a+2)(b+2)
=(a+b)2﹣4ab+ab+2(a+b)+4
=(a+b)2﹣3ab+2(a+b)+4
=52﹣3×5+2×5+4
=24;
②设2024﹣a=x,a﹣2023=y,
∴x+y=2024﹣a+a﹣2023=1,
∵(2024﹣a)2+(a﹣2023)2=7,
∴x2+y2=7,
∴(x+y)2﹣2xy=7,
∴12﹣2xy=7,
∴xy=﹣3,
∴(2024﹣a)(a﹣2023)=﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
一.选择题(共8小题)
1.(2025春 五华区校级期末)已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为( )
A.3 B.4 C.5 D.6
2.(2015春 平顶山期末)下列计算正确的是( )
A.a3+a2=a5 B.a3 a2=a6 C.(a3)2=a9 D.a6÷a2=a4
3.(2024秋 丹巴县期末)若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
4.(2025春 河西区校级期末)《九章算术 盈不足》载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二.问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出11钱,就多了8钱:如果每人出9钱,就少了12钱.问一共有多少人?这个物品的价格是多少?设共有x人,物品的价格为y钱,则可列方程组为( )
A. B.
C. D.
5.(2022春 玉林期末)小华去商店购买A、B两种玩具,共用了12元,A种玩具每件1元,B种玩具每件3元.若每种玩具至少买一件,且A种玩具的数量不少于B种玩具的数量,则小华的购买方案有( )
A.7种 B.6种 C.4种 D.3种
6.(2024春 西青区期末)下列命题中真命题是( )
A.互为相反数的两个数和为0
B.相等的角是对顶角
C.若两个角的和为180°,则这两个角互为邻补角
D.同位角相等
7.(2025春 徐州期末)下列各式不能使用平方差公式的是( )
A.(2a+b)(2a﹣b) B.(2a﹣b)(b﹣2a)
C.(﹣2a+b)(﹣2a﹣b) D.(2a﹣b)(﹣2a﹣b)
8.(2024春 谷城县期末)若关于x的不等式组的解集为x<3,则m的取值范围是( )
A.m>2 B.m≥2 C.m<2 D.m≤2
二.填空题(共8小题)
9.(2025春 成都校级期末)已知27a=81b+1,则9a2﹣16b2﹣32b的值为 .
10.(2021春 顺义区期末)写出一个以为解的二元一次方程 .
11.(2024春 盱眙县期末)不等式2x+3>1的解集为 .
12.(2023秋 蜀山区期末)写出“对顶角相等”的逆命题 .
13.(2024秋 康平县期末)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为 .
14.(2022秋 玉林期末)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为 .
15.(2021春 固始县期末)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE=
16.(2025春 隆昌市校级期末)已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是 .
三.解答题(共7小题)
17.(2024秋 深圳校级期末)解下列方程组:
(1);
(2).
18.(2024春 萍乡期末)如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
19.(2024春 南安市期末)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C,画出△A2B2C.
20.(2022春 泗阳县期末)某零食店购进A、B两种网红零食共100件,A种零食进价为每件8元,B种零食进价为每件5元,在销售过程中,顾客买了3件A种零食和2件B种零食共付款65元,顾客乙买了2件A种零食和3件B种零食共付款60元.
(1)求A、B两种零食每件的售价分别是多少元?
(2)若该零食店计划A、B两种零食的进货总投入不超过656元,且销售完后总利润不低于600元,则购进A、B两种零食有多少种进货方案?
(3)在(2)的条件下,哪种进货方案可使获利最大?最大利润是多少元?
21.(2024春 和县期末)阅读材料:如果x是一个有理数,我们把不超过x的最大整数记作[x].
例如,[3.2]=3,[5]=5,[﹣2.1]=﹣3.
那么,x=[x]+a,其中0≤a<1.
例如,3.2=[3.2]+0.2,5=[5]+0.﹣2.1=[﹣2.1]+0.9.请你解决下列问题:
(1)[4.8]= ,[﹣6.5]= ,[0]= :
(2)如果[x]=3,那么x的取值范围是 ;
(3)如果[5x﹣2]=3x+1,求x的值.
22.(2024春 惠城区校级期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为x>﹣1,请求常数“□”的取值范围.
23.(2024春 贵州期末)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.数学活动课上,老师展示了如图1的长方形纸片,它是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的形状拼成一个正方形,请解答下列问题:
(1)请用两种不同的方法表示图2中阴影部分的面积:
方法1: ;
方法2: .
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 .
(3)结合以上信息,灵活运用公式,解决如下问题:
①已知a+b=5,ab=5,求(a﹣b)2+(a+2)(b+2)的值;
②已知(2024﹣a)2+(a﹣2023)2=7,求(2024﹣a)(a﹣2023)的值.
期末真题重组练习卷-2024-2025学年数学七年级下册苏科版(2024)
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B D C C D A B B
一.选择题(共8小题)
1.(2025春 五华区校级期末)已知(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,则m的值为( )
A.3 B.4 C.5 D.6
【解答】解:∵(m+4)x|m|﹣3+6>0是关于x的一元一次不等式,
∴m+4≠0且|m|﹣3=1,
∴m≠﹣4且m=±4,
∴m=4,
故选:B.
2.(2015春 平顶山期末)下列计算正确的是( )
A.a3+a2=a5 B.a3 a2=a6 C.(a3)2=a9 D.a6÷a2=a4
【解答】解:A、a3+a2不是同类项,不能合并,错误;
B、a3 a2=a5,错误;
C、(a3)2=a6,错误;
D、a6÷a2=a4,正确;
故选:D.
3.(2024秋 丹巴县期末)若是方程3x+ay=1的一个解,则a的值是( )
A.1 B.﹣1 C.2 D.﹣2
【解答】解:把代入方程3x+ay=1得:
﹣3+2a=1,
∴a=2.
故选:C.
4.(2025春 河西区校级期末)《九章算术 盈不足》载,其文曰:“今有共买物,人出十一,盈八;人出九,不足十二.问人数、物价各几何?”意思为:几个人一起去买东西,如果每人出11钱,就多了8钱:如果每人出9钱,就少了12钱.问一共有多少人?这个物品的价格是多少?设共有x人,物品的价格为y钱,则可列方程组为( )
A. B.
C. D.
【解答】解:设共有x人,物品的价格为y钱,根据题意得:
.
故选:C.
5.(2022春 玉林期末)小华去商店购买A、B两种玩具,共用了12元,A种玩具每件1元,B种玩具每件3元.若每种玩具至少买一件,且A种玩具的数量不少于B种玩具的数量,则小华的购买方案有( )
A.7种 B.6种 C.4种 D.3种
【解答】解:设小华购买了A种玩具x件,则购买的B种玩具为件,根据题意得,
,
解得,3≤x≤9,
∵x为整数,也为整数,
∴x=3或6或9,
∴有3种购买方案.
故选:D.
6.(2024春 西青区期末)下列命题中真命题是( )
A.互为相反数的两个数和为0
B.相等的角是对顶角
C.若两个角的和为180°,则这两个角互为邻补角
D.同位角相等
【解答】解:A、互为相反数的两个数和为0,原命题正确,故A选项符合题意;
B、相等的角不一定是对顶角,原命题错误,故B选项不符合题意;
C、若两个角的和为180°,则这两个角互补,不一定是邻补角,原命题错误,故C选项不符合题意;
D、两直线平行,同位角相等,原命题错误,故D选项不符合题意.
故选:A.
7.(2025春 徐州期末)下列各式不能使用平方差公式的是( )
A.(2a+b)(2a﹣b) B.(2a﹣b)(b﹣2a)
C.(﹣2a+b)(﹣2a﹣b) D.(2a﹣b)(﹣2a﹣b)
【解答】解:各式不能使用平方差公式的是(2a﹣b)(b﹣2a),
故选:B.
8.(2024春 谷城县期末)若关于x的不等式组的解集为x<3,则m的取值范围是( )
A.m>2 B.m≥2 C.m<2 D.m≤2
【解答】解:解不等式2x﹣1<5,得:x<3,
∵关于x的不等式组的解集为x<3,
∴m+1≥3,
∴m≥2.
故选:B.
二.填空题(共8小题)
9.(2025春 成都校级期末)已知27a=81b+1,则9a2﹣16b2﹣32b的值为 16 .
【解答】解:∵27a=81b+1,
∴(33)a=(34)b+1,
∴33a=34b+4,
∴3a=4b+4,
∴3a﹣4b=4,
∴9a2﹣16b2﹣32b
=(3a﹣4b)(3a+4b)﹣32b
=4(3a+4b)﹣32b
=12a+16b﹣32b
=12a﹣16b
=4(3a﹣4b)
=4×4
=16,
故答案为:16.
10.(2021春 顺义区期末)写出一个以为解的二元一次方程 2x﹣y=1 .
【解答】解:答案不唯一,如2x﹣y=1.
故答案为:2x﹣y=1.
11.(2024春 盱眙县期末)不等式2x+3>1的解集为 x>﹣1 .
【解答】解:移项,得:2x>1﹣3,
合并同类项,得:2x>﹣2,
系数化为1,得:x>﹣1,
故答案为:x>﹣1.
12.(2023秋 蜀山区期末)写出“对顶角相等”的逆命题 相等的角是对顶角 .
【解答】解:∵原命题的条件是:如果两个角是对顶角,结论是:那么这两个角相等;
∴其逆命题应该为:如两个角相等那么这两个角是对顶角,简化后即为:相等的角是对顶角.
13.(2024秋 康平县期末)如图是由7个形状、大小都相同的小长方形和一块正方形无缝隙拼合而成,则图中阴影部分的面积为 36 .
【解答】解:设小长方形的长为x,宽为y,则小正方形的边长为2y,
依题意得:,
解得:,
∴图中阴影部分的面积为(2y)2=(2×3)2=36.
故答案为:36.
14.(2022秋 玉林期末)我国古代数学名著《孙子算经》中记载了一道题,大意是:100匹马恰好拉了100片瓦,已知1匹大马能拉3片瓦,3匹小马能拉1片瓦,问有多少匹大马、多少匹小马?若设大马有x匹,小马有y匹,那么可列方程组为 .
【解答】解:设大马有x匹,小马有y匹,由题意得:
,
故答案为:.
15.(2021春 固始县期末)如图,将△ABC沿射线AB的方向平移到△DEF的位置,点A、B、C的对应点分别为点D、E、F,若∠ABC=75°,则∠CFE= 105°
【解答】解:由平移可知∠DEF=∠ABC=75°,
∵BE∥CF,
∴∠EFC=180°﹣∠DEF=180°﹣75°=105°.
故答案为:105°.
16.(2025春 隆昌市校级期末)已知关于x,y的二元一次方程组的解为,则关于m,n的方程组的解是 .
【解答】解:设,
可得,
解得:,
故答案为:.
三.解答题(共7小题)
17.(2024秋 深圳校级期末)解下列方程组:
(1);
(2).
【解答】解:(1),
①代入②,可得:3(y+1)﹣4y=﹣2,
解得y=5,
把y=5代入①,解得x=5+1=6,
∴原方程组的解是.
(2),
由①,可得3x﹣2y=8③,
②+③,可得6x=18,
解得x=3,
把x=3代入②,可得:3×3+2y=10,
解得y=0.5,
∴原方程组的解是.
18.(2024春 萍乡期末)如图,已知AD是△ABC的角平分线,AD的垂直平分线交AB于点F,交BC的延长线于点E,连接AE、DF.试说明:
(1)∠EAD=∠EDA;
(2)DF∥AC.
【解答】证明:(1)∵EF是AD的垂直平分线,
∴EA=ED,
∴∠EAD=∠EDA;
(2)∵EF是AD的垂直平分线,
∴FA=FD,
∴∠FDA=∠FAD,
∵AD平分∠BAC,
∴∠FAD=∠CAD,
∴∠FDA=∠CAD,
∴DF∥AC.
19.(2024春 南安市期末)如图,网格中每个小正方形的边长均为1,△ABC的顶点均在小正方形的格点上.
(1)将△ABC向下平移3个单位长度得到△A1B1C1,画出△A1B1C1;
(2)将△ABC绕点C顺时针旋转90°得到△A2B2C,画出△A2B2C.
【解答】解:(1)如图,△A1B1C1即为所求.
(2)如图,△A2B2C即为所求.
20.(2022春 泗阳县期末)某零食店购进A、B两种网红零食共100件,A种零食进价为每件8元,B种零食进价为每件5元,在销售过程中,顾客买了3件A种零食和2件B种零食共付款65元,顾客乙买了2件A种零食和3件B种零食共付款60元.
(1)求A、B两种零食每件的售价分别是多少元?
(2)若该零食店计划A、B两种零食的进货总投入不超过656元,且销售完后总利润不低于600元,则购进A、B两种零食有多少种进货方案?
(3)在(2)的条件下,哪种进货方案可使获利最大?最大利润是多少元?
【解答】解:(1)设A种零食每件的售价是x元,B种零食每件的售价是y元,
根据题意得:,
解得,
答:A种零食每件的售价是15元,B种零食每件的售价是10元;
(2)设购进A种零食m件,则购进B种零食(100﹣m)件,
∵进货总投入不超过656元,且销售完后总利润不低于600元,
∴,
解得50≤m≤52,
∵m为整数,
∴m可取50,51,52,
∴购进A、B两种零食有3种进货方案:
①购进A种零食50件,购进B种零食50件;
②购进A种零食51件,购进B种零食49件;
③购进A种零食52件,购进B种零食48件;
(3)设获利w元,
购进A种零食50件,购进B种零食50件,w=(15﹣8)×50+(10﹣5)×50=600(元),
购进A种零食51件,购进B种零食49件,w=(15﹣8)×51+(10﹣5)×49=602(元),
购进A种零食52件,购进B种零食48件,w=(15﹣8)×52+(10﹣5)×48=604(元),
∵600<602<604,
∴购进A种零食52件,购进B种零食48件,获利最大,最大利润是604元.
21.(2024春 和县期末)阅读材料:如果x是一个有理数,我们把不超过x的最大整数记作[x].
例如,[3.2]=3,[5]=5,[﹣2.1]=﹣3.
那么,x=[x]+a,其中0≤a<1.
例如,3.2=[3.2]+0.2,5=[5]+0.﹣2.1=[﹣2.1]+0.9.请你解决下列问题:
(1)[4.8]= 4 ,[﹣6.5]= ﹣7 ,[0]= 0 :
(2)如果[x]=3,那么x的取值范围是 3≤x<4 ;
(3)如果[5x﹣2]=3x+1,求x的值.
【解答】解:(1)[4.8]=4,[﹣6.5]=﹣7,[0]=0,
故答案为:4,﹣7,0;
(2)如果[x]=3,那么x的取值范围是3≤x<4,
故答案为:3≤x<4;
(3)∵[5x﹣2]=3x+1,
∴3x+1≤5x﹣2<3x+2.
解得x<2,
∵3x+1是整数,
∴x.
22.(2024春 惠城区校级期末)嘉淇准备完成题目:解不等式组时,发现常数“□”印刷不清楚.
(1)他把“□”猜成3,请你解不等式组;
(2)王老师说:我做一下变式,若不等式组的解集为x>﹣1,请求常数“□”的取值范围.
【解答】解:(1),
解不等式2x﹣4<3(x﹣1)得,
∴2x﹣4<3x﹣3,
∴x>﹣1,
解不等式得,
∴2x﹣6>x﹣4,
∴x>2,
∴不等式组的解集为x>2;
(2),
设常数“□”为m,
∵,
∴2x﹣2m>x﹣4,
∴x>2m﹣4,
∴不等式的解集为x>2m﹣4,
又∵不等式2x﹣4<3(x﹣1)的解集为x>﹣1,
而不等式组的解集为x>﹣1,
∴﹣1≥2m﹣4,
∴,
∴.
23.(2024春 贵州期末)通常,用两种不同的方法计算同一个图形的面积,可以得到一个恒等式.数学活动课上,老师展示了如图1的长方形纸片,它是一个长为2a,宽为2b的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图2的形状拼成一个正方形,请解答下列问题:
(1)请用两种不同的方法表示图2中阴影部分的面积:
方法1: (a﹣b)2 ;
方法2: (a+b)2﹣4ab .
(2)观察图2,请你写出(a+b)2、(a﹣b)2、ab之间的等量关系是 (a﹣b)2=(a+b)2﹣4ab .
(3)结合以上信息,灵活运用公式,解决如下问题:
①已知a+b=5,ab=5,求(a﹣b)2+(a+2)(b+2)的值;
②已知(2024﹣a)2+(a﹣2023)2=7,求(2024﹣a)(a﹣2023)的值.
【解答】解:(1)方法一:阴影部分是边长为a﹣b的正方形,因此面积为(a﹣b)2,
方法二:阴影部分的面积可以看作从边长为a+b的正方形面积减去4个长a,宽为b的长方形面积,即(a+b)2﹣4ab;
故答案为:(a﹣b)2,(a+b)2﹣4ab;
(2)由(1)得,(a﹣b)2=(a+b)2﹣4ab,
故答案为:(a﹣b)2=(a+b)2﹣4ab;
(3)①∵a+b=5,ab=5,
∴(a﹣b)2+(a+2)(b+2)
=(a+b)2﹣4ab+ab+2(a+b)+4
=(a+b)2﹣3ab+2(a+b)+4
=52﹣3×5+2×5+4
=24;
②设2024﹣a=x,a﹣2023=y,
∴x+y=2024﹣a+a﹣2023=1,
∵(2024﹣a)2+(a﹣2023)2=7,
∴x2+y2=7,
∴(x+y)2﹣2xy=7,
∴12﹣2xy=7,
∴xy=﹣3,
∴(2024﹣a)(a﹣2023)=﹣3.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
