期末真题重组练习卷-2024-2025学年数学八年级下册北师大版(含详解)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年数学八年级下册北师大版(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:47:58 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学八年级下册北师大版
一.选择题(共8小题)
1.(2024春 历城区期末)《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
2.(2024春 织金县期末)计算的结果等于( )
A.﹣1 B.1 C.x﹣1 D.
3.(2024春 易门县期末)C60是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是C60的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A.60° B.72° C.108° D.120°
4.(2023秋 邗江区期末)一次函数y=ax+b的自变量和函数值的部分对应值如下表所示:
x 0 5
y 3 5
则关于x的不等式ax+b>x的解集是( )
A.x<5 B.x>5 C.x<0 D.x>0
5.(2024秋 天山区校级期末)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
6.(2024秋 岱岳区期末)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=12m,则A,B之间的距离是( )
A.48m B.24m C.12m D.6m
7.(2023秋 兰陵县期末)点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
8.(2022春 福田区校级期末)如图,在平行四边形ABCD中,对角线BD=8,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,若GA=3,则AD的长是( )
A.3 B.4 C.5 D.3
二.填空题(共8小题)
9.(2023秋 互助县期末)分解因式:x2﹣1= .
10.(2024秋 鄂州期末)若代数式有意义,则实数x的取值范围是 .
11.(2025春 虹口区校级期末)关于x的不等式组的解集是x>5,则a= .
12.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: .
13.(2024春 曲阜市期末)如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
14.(2023秋 东营期末)如图,在平行四边形ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
15.(2024春 三明期末)如图,直线与y2=﹣x+a相交于点P(2,m),则关于x的不等式的解集是 .
16.(2024春 新郑市期末)如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,点H,G分别是边DC,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为 .
三.解答题(共11小题)
17.(2024春 中牟县期末)把下列各式因式分解:
(1)﹣16m3+16m2﹣4m;
(2)9(x+y)2﹣4y2.
18.(2024春 涞源县期末)解方程:1.
19.(2024春 福田区校级期末)解不等式组,并把解集在数轴上表示出来.
20.(2024春 海沧区期末)先化简,再求值:,其中.
21.(2024春 蓬江区校级期末)如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
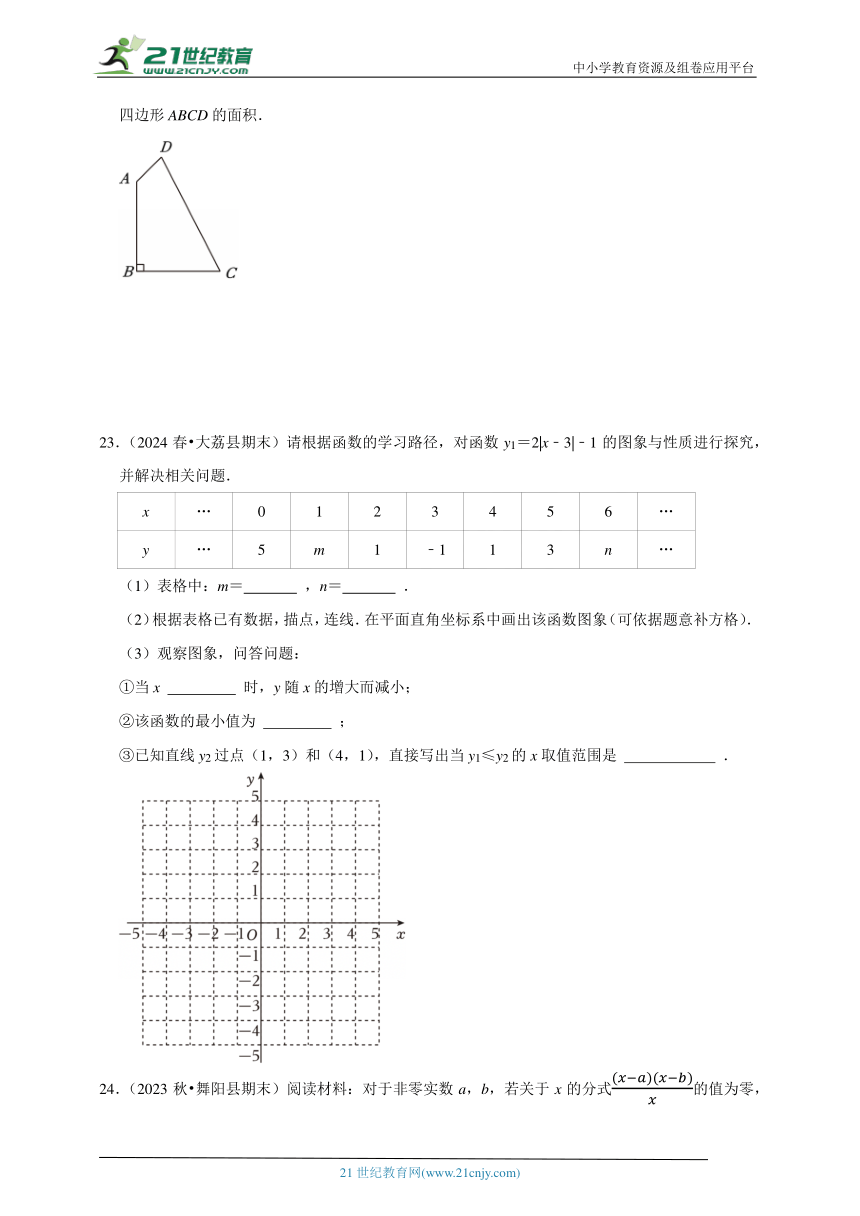
22.(2024春 博兴县期末)如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
23.(2024春 大荔县期末)请根据函数的学习路径,对函数y1=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.
x … 0 1 2 3 4 5 6 …
y … 5 m 1 ﹣1 1 3 n …
(1)表格中:m= ,n= .
(2)根据表格已有数据,描点,连线.在平面直角坐标系中画出该函数图象(可依据题意补方格).
(3)观察图象,问答问题:
①当x 时,y随x的增大而减小;
②该函数的最小值为 ;
③已知直线y2过点(1,3)和(4,1),直接写出当y1≤y2的x取值范围是 .
24.(2023秋 舞阳县期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为(a+b),所以关于x的方程xa+b的解为x1=a,x2=b.
(1)理解应用:方程的解为:x1= ,x2= ;
(2)知识迁移:若关于x的方程x7的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+4t3的值.
25.(2024春 中牟县期末)2020年12月28日,习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买A型和B型两种农机具,已知1件A型农机具比1件B型农机具多0.5万元,用18万元购买A型农机具和15万元购买B型农机具的数量相同.
(1)求购买1件A型农机具和1件B型农机具各需多少钱?
(2)若该粮食生产基地计划购买A型和B型两种农机具共24件,且购买的总费用不超过66万元,购买A型农机具最多能购买多少件?
26.(2024春 涞源县期末)阅读理解
下列一组方程:①x3,②x5,③x7,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解,他的解过程如下:
由①x1+2得x=1或x=2;
由②x2+3得x=2或x=3;
由③x3+4得x=3或x=4.
(1)问题解决:请写出第四个方程,并按照小明的解题思路求出该方程的解;
(2)规律探究:若n为正整数,请写出第n个方程及其方程的解;
(3)变式拓展:若n为正整数,关于x的方程x2n﹣1的一个解是x=10,求n的值.
27.(2024春 阳谷县期末)如图1,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别记为a、b、c.
实验一:
小聪和小明用八张这样的三角形纸片拼出了如图2所示的正方形.
(1)在图2中,正方形CDEF的面积可表示为 ,正方形IJKL的面积可表示为 (用含a,b的式子表示)
(2)请结合图2,用面积法说明(a+b)2,ab,(a﹣b)2三者之间的等量关系.
实验二:
小聪和小明分别用四个这样三角形纸片拼成了如图3所示的图形.他们根据面积法得到了一个关于边a、b、c的等式,整理后发现a2+b2=c2.
(3)请你用面积法证明a2+b2=c2.
期末真题重组练习卷-2024-2025学年数学八年级下册北师大版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A D A A B C B
一.选择题(共8小题)
1.(2024春 历城区期末)《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
【解答】解:A、不是中心对称图形,故选项错误,不符合题意;
B、是中心对称图形,故选项正确,符合题意;
C、不是中心对称图形,故本选项错误,不符合题意;
D、不是中心对称图形,故本选项错误,不符合题意.
故选:B.
2.(2024春 织金县期末)计算的结果等于( )
A.﹣1 B.1 C.x﹣1 D.
【解答】解:原式1,
故选:A.
3.(2024春 易门县期末)C60是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是C60的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A.60° B.72° C.108° D.120°
【解答】解:∵正六边形的内角和为:(6﹣2)×180°=720°,
又∵正六边形的6个内角都相等,
∴正六边形的每一个内角的度数是:720÷6=120°.
故选:D.
4.(2023秋 邗江区期末)一次函数y=ax+b的自变量和函数值的部分对应值如下表所示:
x 0 5
y 3 5
则关于x的不等式ax+b>x的解集是( )
A.x<5 B.x>5 C.x<0 D.x>0
【解答】解:由题意得:5k+3=5,解得:k=0.4,
∴y=0.4x+3,
∴0.4x+3>x,
解得:x<5,
故选:A.
5.(2024秋 天山区校级期末)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
【解答】解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
2,
故选:A.
6.(2024秋 岱岳区期末)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=12m,则A,B之间的距离是( )
A.48m B.24m C.12m D.6m
【解答】解:∵C,D是OA,OB的中点,
∴CD是△OAB的中位线,
∴AB=2CD=2×12=24(m),
故选:B.
7.(2023秋 兰陵县期末)点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
【解答】解:已知点P(2,﹣3),
则点P关于原点对称的点的坐标是(﹣2,3),
故选:C.
8.(2022春 福田区校级期末)如图,在平行四边形ABCD中,对角线BD=8,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,若GA=3,则AD的长是( )
A.3 B.4 C.5 D.3
【解答】解:由作图可知:EF是线段AB的垂直平分线,
∴BG=GA=3,
∴DG=BD﹣BG=8﹣3=5.
∵GA⊥AD,
∴∠GAD=90°,
在Rt△ADG中,由勾股定理,得,
AD4.
故选:B.
二.填空题(共8小题)
9.(2023秋 互助县期末)分解因式:x2﹣1= (x+1)(x﹣1) .
【解答】解:x2﹣1=(x+1)(x﹣1).
故答案为:(x+1)(x﹣1).
10.(2024秋 鄂州期末)若代数式有意义,则实数x的取值范围是 x≠2 .
【解答】解:要使代数式有意义,只需x﹣2≠0,
∴x≠2,
则实数x的取值范围是x≠2,
故答案为:x≠2.
11.(2025春 虹口区校级期末)关于x的不等式组的解集是x>5,则a= 2 .
【解答】解:∵不等式组的解集为x>5,
∴3a﹣1<a+1=5,或a+1<3a﹣1=5,
a+1=5,解得a=4,3a﹣1>a+1,不满足条件,
3a﹣1=5,解得a=2,a+1<3a﹣1,满足条件,
∴综上所述,a=2.
故答案为:2.
12.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: 3y2﹣5y﹣1=0 .
【解答】解:由题意可得:,
方程两边同乘以y,得3y2﹣1=5y,
则3y2﹣5y﹣1=0,
故答案为:3y2﹣5y﹣1=0.
13.(2024春 曲阜市期末)如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 (0,3)或(﹣4,0) .
【解答】解:设平移后点P、Q的对应点分别是P′、Q′.
分两种情况:
①P′在y轴上,Q′在x轴上,
则P′横坐标为0,Q′纵坐标为0,
∵0﹣(n﹣3)=﹣n+3,
∴n﹣n+3=3,
∴点P平移后的对应点的坐标是(0,3);
②P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
综上可知,点P平移后的对应点的坐标是(0,3)或(﹣4,0).
故答案为:(0,3)或(﹣4,0).
14.(2023秋 东营期末)如图,在平行四边形ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 36 .
【解答】解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC∠ABC,∠ECB∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=3,
同理可证 DE=DC=3,
∴DE+AE=AD=6,
∴BE2+CE2=BC2=AD2=36.
故答案为:36.
15.(2024春 三明期末)如图,直线与y2=﹣x+a相交于点P(2,m),则关于x的不等式的解集是 x>2 .
【解答】】解:根据图象可得:不等式的解集是x>2.
故答案为:x>2.
16.(2024春 新郑市期末)如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,点H,G分别是边DC,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为 .
【解答】解:如图,连接AG,过点A作AG′⊥BC于G′,
∵点E为AH的中点,点F为GH的中点,
∴EF是△AGH的中位线,
∴EFAG,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=120°,
∴∠B=60°,
∴∠BAG′=30°,
∴BG′AB=1,
由勾股定理得:AG′,
由垂线段最短可知,当点G在G′位置时,AG最小,
∴EF的最小值为,
故答案为:.
三.解答题(共11小题)
17.(2024春 中牟县期末)把下列各式因式分解:
(1)﹣16m3+16m2﹣4m;
(2)9(x+y)2﹣4y2.
【解答】解:(1)原式=﹣4m(4m2﹣4m+1)=﹣4m(2m﹣1)2.
(2)原式=[3(x+y)+2y][3(x+y)﹣2y]=(3x+5y)(3x+y).
18.(2024春 涞源县期末)解方程:1.
【解答】解:对分母进行因式分解,得1,
方程的两边都乘以(x+3)(x﹣3),得:(x+1)(x﹣3)﹣12=(x+3)(x﹣3),
去括号,得:x2﹣3x+x﹣3﹣12=x2﹣9,
移项,得:x2﹣x2﹣3x+x=﹣9+3+12,
合并同类项,得:﹣2x=6,
系数化为1,得:x=﹣3.
检验:当x=﹣3时,(x+3)(x﹣3)=0,所以x=﹣3是原方程的增根,
所以,原方程无解.
19.(2024春 福田区校级期末)解不等式组,并把解集在数轴上表示出来.
【解答】解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
20.(2024春 海沧区期末)先化简,再求值:,其中.
【解答】解:
,
当x1时,原式.
21.(2024春 蓬江区校级期末)如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
【解答】(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)解:∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DEBG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF(AB﹣AG)(AB﹣AC)(10﹣4)=3.
22.(2024春 博兴县期末)如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
【解答】解:连接AC,
∵∠B=90°,AB=BC=2,
∴AC=2,∠BAC=45°,
∵AD=1,CD=3,
∴AD2+AC2=12+(2)2,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
在Rt△ABC中,S△ABCBC AB2×2=2,
在Rt△ADC中,S△ADCAD AC1×2,
∴S四边形ABCD=S△ABC+S△ADC=2.
23.(2024春 大荔县期末)请根据函数的学习路径,对函数y1=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.
x … 0 1 2 3 4 5 6 …
y … 5 m 1 ﹣1 1 3 n …
(1)表格中:m= 3 ,n= 5 .
(2)根据表格已有数据,描点,连线.在平面直角坐标系中画出该函数图象(可依据题意补方格).
(3)观察图象,问答问题:
①当x ≤3 时,y随x的增大而减小;
②该函数的最小值为 ﹣1 ;
③已知直线y2过点(1,3)和(4,1),直接写出当y1≤y2的x取值范围是 1≤x≤4 .
【解答】解:(1)当x=1时,m=2×|1﹣3|﹣1=3,
当x=6时,n=2×|6﹣3|﹣1=5,
故答案为:3,5;
(2)根据表中数据,描点,连线如图所示:
(3)解:①由图可知,由图可知,当x≤3时,y随x的增大而减小,
故答案为:x≤3;
②当x=3时,函数值y最小,最小值为﹣1.
故答案为:﹣1;
③∵直线y2过点(1,3)和(4,1),如图所示,
∴当y1≤y2的x取值范围是1≤x≤4,
故答案为:1≤x≤4.
24.(2023秋 舞阳县期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为(a+b),所以关于x的方程xa+b的解为x1=a,x2=b.
(1)理解应用:方程的解为:x1= 5 ,x2= ;
(2)知识迁移:若关于x的方程x7的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+4t3的值.
【解答】解:(1)∵xa+b的解为x1=a,x2=b,
∴5的解为x=5或x,
故答案为:5,;
(2)∵方程x7,
∴a+b=7,ab=3,
∴a2+b2=(a+b)2﹣2ab=49﹣6=43;
(3)方程k﹣x可化为x﹣1k﹣1,
设y=x﹣1,方程变形为yk﹣1,
∴y1 y2=6,y1+y2=k﹣1,
∴y1=x1﹣1,y2=x2﹣1,
∵x1=t+1,x2=t2+2,
∴y1=t+1﹣t=t,,
∴x﹣1=t或x﹣1=t2+1,
∴t(t2+1)=6,t+t2+1=k﹣1,
∴k=t+t2+2,t3+t=6,
k2﹣4k+4t3
=k(k﹣4)+4t3
=(t+t2+2)(t+t2﹣2)+4t3
=t4+6t3+t2﹣4
=t(t3+t)+6t3﹣4
=6t+6t3﹣4
=6(t3+t)﹣4
=6×6﹣4
=32.
25.(2024春 中牟县期末)2020年12月28日,习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买A型和B型两种农机具,已知1件A型农机具比1件B型农机具多0.5万元,用18万元购买A型农机具和15万元购买B型农机具的数量相同.
(1)求购买1件A型农机具和1件B型农机具各需多少钱?
(2)若该粮食生产基地计划购买A型和B型两种农机具共24件,且购买的总费用不超过66万元,购买A型农机具最多能购买多少件?
【解答】解:(1)设购买一件A型农机具需要x万元,购买一件B型农机具需要(x﹣0.5)万元,
根据题意,得.
解这个方程得x=3,
经检验,x=3是原方程的解,
x﹣0.5=2.5(万元),
所以,购买一件A型农机具需要3万元,购买一件B型农机具需要2.5万元;
(2)设购买A型农机具m件,
根据题意,得3m+2.5(24﹣m)≤66,
解这个不等式,得m≤12.
所以,最多可以购买12件A型农机具.
26.(2024春 涞源县期末)阅读理解
下列一组方程:①x3,②x5,③x7,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解,他的解过程如下:
由①x1+2得x=1或x=2;
由②x2+3得x=2或x=3;
由③x3+4得x=3或x=4.
(1)问题解决:请写出第四个方程,并按照小明的解题思路求出该方程的解;
(2)规律探究:若n为正整数,请写出第n个方程及其方程的解;
(3)变式拓展:若n为正整数,关于x的方程x2n﹣1的一个解是x=10,求n的值.
【解答】解:(1)由①x1+2得x=1或x=2;
由②x+x2+3得x=2或x=3;
由③x3+4得x=3或x=4,
则第四个方程为:x4+5,即x9,
由x4+5得:x=4或x=5;
(2)可得第n个方程为:x2n+1,
解得:x=n或x=n+1;
(3)将原方程变形,(x+2)n+(2n+1),
∴x+2=n或x+2=2n+1,
∴方程的解是x=n﹣2,或x=2n﹣1,
当n﹣2=10时,n=12,
当2n﹣1=10时,n=5.5,
∴n的值是12或5.5.
27.(2024春 阳谷县期末)如图1,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别记为a、b、c.
实验一:
小聪和小明用八张这样的三角形纸片拼出了如图2所示的正方形.
(1)在图2中,正方形CDEF的面积可表示为 (a+b)2 ,正方形IJKL的面积可表示为 (a﹣b)2 (用含a,b的式子表示)
(2)请结合图2,用面积法说明(a+b)2,ab,(a﹣b)2三者之间的等量关系.
实验二:
小聪和小明分别用四个这样三角形纸片拼成了如图3所示的图形.他们根据面积法得到了一个关于边a、b、c的等式,整理后发现a2+b2=c2.
(3)请你用面积法证明a2+b2=c2.
【解答】解:(1)∵正方形CDEF的边长为a+b,
∴正方形CDEF的面积为(a+b)2.
∵正方形IJKL的边长为a﹣b,
∴正方形IJKL的面积为(a﹣b)2.
故答案为:(a+b)2,(a﹣b)2;
(2)由图2可以看出,正方形CDEF的面积﹣正方形IJKL的面积=4个矩形的面积.
∴(a+b)2﹣(a﹣b)2=4ab;
(3)∵S五边形BCFGI=S正方形BCED+S正方形HEFG+S△BID+S△IHG=S正方形ABIG+S△ABC+S△AGF,
∴a2+b2abab=c2abab.
∴a2+b2=c2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学八年级下册北师大版
一.选择题(共8小题)
1.(2024春 历城区期末)《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
2.(2024春 织金县期末)计算的结果等于( )
A.﹣1 B.1 C.x﹣1 D.
3.(2024春 易门县期末)C60是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是C60的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A.60° B.72° C.108° D.120°
4.(2023秋 邗江区期末)一次函数y=ax+b的自变量和函数值的部分对应值如下表所示:
x 0 5
y 3 5
则关于x的不等式ax+b>x的解集是( )
A.x<5 B.x>5 C.x<0 D.x>0
5.(2024秋 天山区校级期末)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
6.(2024秋 岱岳区期末)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=12m,则A,B之间的距离是( )
A.48m B.24m C.12m D.6m
7.(2023秋 兰陵县期末)点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
8.(2022春 福田区校级期末)如图,在平行四边形ABCD中,对角线BD=8,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,若GA=3,则AD的长是( )
A.3 B.4 C.5 D.3
二.填空题(共8小题)
9.(2023秋 互助县期末)分解因式:x2﹣1= .
10.(2024秋 鄂州期末)若代数式有意义,则实数x的取值范围是 .
11.(2025春 虹口区校级期末)关于x的不等式组的解集是x>5,则a= .
12.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: .
13.(2024春 曲阜市期末)如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 .
14.(2023秋 东营期末)如图,在平行四边形ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 .
15.(2024春 三明期末)如图,直线与y2=﹣x+a相交于点P(2,m),则关于x的不等式的解集是 .
16.(2024春 新郑市期末)如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,点H,G分别是边DC,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为 .
三.解答题(共11小题)
17.(2024春 中牟县期末)把下列各式因式分解:
(1)﹣16m3+16m2﹣4m;
(2)9(x+y)2﹣4y2.
18.(2024春 涞源县期末)解方程:1.
19.(2024春 福田区校级期末)解不等式组,并把解集在数轴上表示出来.
20.(2024春 海沧区期末)先化简,再求值:,其中.
21.(2024春 蓬江区校级期末)如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
22.(2024春 博兴县期末)如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
23.(2024春 大荔县期末)请根据函数的学习路径,对函数y1=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.
x … 0 1 2 3 4 5 6 …
y … 5 m 1 ﹣1 1 3 n …
(1)表格中:m= ,n= .
(2)根据表格已有数据,描点,连线.在平面直角坐标系中画出该函数图象(可依据题意补方格).
(3)观察图象,问答问题:
①当x 时,y随x的增大而减小;
②该函数的最小值为 ;
③已知直线y2过点(1,3)和(4,1),直接写出当y1≤y2的x取值范围是 .
24.(2023秋 舞阳县期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为(a+b),所以关于x的方程xa+b的解为x1=a,x2=b.
(1)理解应用:方程的解为:x1= ,x2= ;
(2)知识迁移:若关于x的方程x7的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+4t3的值.
25.(2024春 中牟县期末)2020年12月28日,习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买A型和B型两种农机具,已知1件A型农机具比1件B型农机具多0.5万元,用18万元购买A型农机具和15万元购买B型农机具的数量相同.
(1)求购买1件A型农机具和1件B型农机具各需多少钱?
(2)若该粮食生产基地计划购买A型和B型两种农机具共24件,且购买的总费用不超过66万元,购买A型农机具最多能购买多少件?
26.(2024春 涞源县期末)阅读理解
下列一组方程:①x3,②x5,③x7,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解,他的解过程如下:
由①x1+2得x=1或x=2;
由②x2+3得x=2或x=3;
由③x3+4得x=3或x=4.
(1)问题解决:请写出第四个方程,并按照小明的解题思路求出该方程的解;
(2)规律探究:若n为正整数,请写出第n个方程及其方程的解;
(3)变式拓展:若n为正整数,关于x的方程x2n﹣1的一个解是x=10,求n的值.
27.(2024春 阳谷县期末)如图1,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别记为a、b、c.
实验一:
小聪和小明用八张这样的三角形纸片拼出了如图2所示的正方形.
(1)在图2中,正方形CDEF的面积可表示为 ,正方形IJKL的面积可表示为 (用含a,b的式子表示)
(2)请结合图2,用面积法说明(a+b)2,ab,(a﹣b)2三者之间的等量关系.
实验二:
小聪和小明分别用四个这样三角形纸片拼成了如图3所示的图形.他们根据面积法得到了一个关于边a、b、c的等式,整理后发现a2+b2=c2.
(3)请你用面积法证明a2+b2=c2.
期末真题重组练习卷-2024-2025学年数学八年级下册北师大版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 B A D A A B C B
一.选择题(共8小题)
1.(2024春 历城区期末)《国家宝藏》节目立足于中华文化宝库资源,通过对文物的梳理与总结,演绎文物背后的故事与历史,让更多的观众走进博物馆,让一个个馆藏文物鲜活起来.下面四幅图是我国一些博物馆的标志,其中是中心对称图形的是( )
A. B. C. D.
【解答】解:A、不是中心对称图形,故选项错误,不符合题意;
B、是中心对称图形,故选项正确,符合题意;
C、不是中心对称图形,故本选项错误,不符合题意;
D、不是中心对称图形,故本选项错误,不符合题意.
故选:B.
2.(2024春 织金县期末)计算的结果等于( )
A.﹣1 B.1 C.x﹣1 D.
【解答】解:原式1,
故选:A.
3.(2024春 易门县期末)C60是单纯由碳原子结合形成的稳定分子,它的发现最初始于天文学领域的研究,由英国、美国科学家探明和勾画其碳分子结构,于1985年正式制得,它的发现使人类了解到一个全新的碳世界.如图是C60的分子结构图,它具有60个顶点和32个面,其中12个为正五边形,20个为正六边形,其中正六边形的每一个内角的度数是( )
A.60° B.72° C.108° D.120°
【解答】解:∵正六边形的内角和为:(6﹣2)×180°=720°,
又∵正六边形的6个内角都相等,
∴正六边形的每一个内角的度数是:720÷6=120°.
故选:D.
4.(2023秋 邗江区期末)一次函数y=ax+b的自变量和函数值的部分对应值如下表所示:
x 0 5
y 3 5
则关于x的不等式ax+b>x的解集是( )
A.x<5 B.x>5 C.x<0 D.x>0
【解答】解:由题意得:5k+3=5,解得:k=0.4,
∴y=0.4x+3,
∴0.4x+3>x,
解得:x<5,
故选:A.
5.(2024秋 天山区校级期末)《九章算术》中记录的一道题译为白话文是:把一份文件用慢马送到900里外的城市,需要的时间比规定时间多一天,如果用快马送,所需的时间比规定时间少3天,已知快马的速度是慢马的2倍,求规定时间.设规定时间为x天,则可列方程为( )
A. B.
C. D.
【解答】解:设规定时间为x天,则快马所需的时间为(x﹣3)天,慢马所需的时间为(x+1)天,由题意得:
2,
故选:A.
6.(2024秋 岱岳区期末)如图,为测量位于一水塘旁的两点A,B间的距离,在地面上确定点O,分别取OA,OB的中点C,D,量得CD=12m,则A,B之间的距离是( )
A.48m B.24m C.12m D.6m
【解答】解:∵C,D是OA,OB的中点,
∴CD是△OAB的中位线,
∴AB=2CD=2×12=24(m),
故选:B.
7.(2023秋 兰陵县期末)点P(2,﹣3)关于原点对称的点的坐标是( )
A.(﹣2,﹣3) B.(2,3) C.(﹣2,3) D.(﹣3,2)
【解答】解:已知点P(2,﹣3),
则点P关于原点对称的点的坐标是(﹣2,3),
故选:C.
8.(2022春 福田区校级期末)如图,在平行四边形ABCD中,对角线BD=8,分别以点A,B为圆心,以大于AB的长为半径画弧,两弧相交于点E和点F,作直线EF,交对角线BD于点G,连接GA,GA恰好垂直于边AD,若GA=3,则AD的长是( )
A.3 B.4 C.5 D.3
【解答】解:由作图可知:EF是线段AB的垂直平分线,
∴BG=GA=3,
∴DG=BD﹣BG=8﹣3=5.
∵GA⊥AD,
∴∠GAD=90°,
在Rt△ADG中,由勾股定理,得,
AD4.
故选:B.
二.填空题(共8小题)
9.(2023秋 互助县期末)分解因式:x2﹣1= (x+1)(x﹣1) .
【解答】解:x2﹣1=(x+1)(x﹣1).
故答案为:(x+1)(x﹣1).
10.(2024秋 鄂州期末)若代数式有意义,则实数x的取值范围是 x≠2 .
【解答】解:要使代数式有意义,只需x﹣2≠0,
∴x≠2,
则实数x的取值范围是x≠2,
故答案为:x≠2.
11.(2025春 虹口区校级期末)关于x的不等式组的解集是x>5,则a= 2 .
【解答】解:∵不等式组的解集为x>5,
∴3a﹣1<a+1=5,或a+1<3a﹣1=5,
a+1=5,解得a=4,3a﹣1>a+1,不满足条件,
3a﹣1=5,解得a=2,a+1<3a﹣1,满足条件,
∴综上所述,a=2.
故答案为:2.
12.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: 3y2﹣5y﹣1=0 .
【解答】解:由题意可得:,
方程两边同乘以y,得3y2﹣1=5y,
则3y2﹣5y﹣1=0,
故答案为:3y2﹣5y﹣1=0.
13.(2024春 曲阜市期末)如图第一象限内有两点P(m﹣4,n),Q(m,n﹣3),将线段PQ平移,使点P、Q分别落在两条坐标轴上,则点P平移后的对应点的坐标是 (0,3)或(﹣4,0) .
【解答】解:设平移后点P、Q的对应点分别是P′、Q′.
分两种情况:
①P′在y轴上,Q′在x轴上,
则P′横坐标为0,Q′纵坐标为0,
∵0﹣(n﹣3)=﹣n+3,
∴n﹣n+3=3,
∴点P平移后的对应点的坐标是(0,3);
②P′在x轴上,Q′在y轴上,
则P′纵坐标为0,Q′横坐标为0,
∵0﹣m=﹣m,
∴m﹣4﹣m=﹣4,
∴点P平移后的对应点的坐标是(﹣4,0);
综上可知,点P平移后的对应点的坐标是(0,3)或(﹣4,0).
故答案为:(0,3)或(﹣4,0).
14.(2023秋 东营期末)如图,在平行四边形ABCD中,AB=3,∠ABC的平分线与∠BCD的平分线交于点E,若点E恰好在边AD上,则BE2+CE2的值为 36 .
【解答】解:∵BE、CE 分别平分∠ABC 和∠BCD
∴∠EBC∠ABC,∠ECB∠BCD,
∵四边形ABCD是平行四边形,
∴AD∥BC,AB=CD=2,BC=AD,
∴∠ABC+∠BCD=180°,
∴∠EBC+∠ECB=90°,
∴∠BEC=90°,
∴BE2+CE2=BC2 ,
∵AD∥BC,
∴∠EBC=∠AEB,
∵BE平分∠ABC,
∴∠EBC=∠ABE,
∴∠AEB=∠ABE,
∴AB=AE=3,
同理可证 DE=DC=3,
∴DE+AE=AD=6,
∴BE2+CE2=BC2=AD2=36.
故答案为:36.
15.(2024春 三明期末)如图,直线与y2=﹣x+a相交于点P(2,m),则关于x的不等式的解集是 x>2 .
【解答】】解:根据图象可得:不等式的解集是x>2.
故答案为:x>2.
16.(2024春 新郑市期末)如图,在 ABCD中,∠C=120°,AB=2,AD=2AB,点H,G分别是边DC,BC上的动点,连接AH,HG,点E为AH的中点,点F为GH的中点,连接EF,则EF的最小值为 .
【解答】解:如图,连接AG,过点A作AG′⊥BC于G′,
∵点E为AH的中点,点F为GH的中点,
∴EF是△AGH的中位线,
∴EFAG,
∵四边形ABCD为平行四边形,
∴AB∥CD,
∴∠B+∠C=180°,
∵∠C=120°,
∴∠B=60°,
∴∠BAG′=30°,
∴BG′AB=1,
由勾股定理得:AG′,
由垂线段最短可知,当点G在G′位置时,AG最小,
∴EF的最小值为,
故答案为:.
三.解答题(共11小题)
17.(2024春 中牟县期末)把下列各式因式分解:
(1)﹣16m3+16m2﹣4m;
(2)9(x+y)2﹣4y2.
【解答】解:(1)原式=﹣4m(4m2﹣4m+1)=﹣4m(2m﹣1)2.
(2)原式=[3(x+y)+2y][3(x+y)﹣2y]=(3x+5y)(3x+y).
18.(2024春 涞源县期末)解方程:1.
【解答】解:对分母进行因式分解,得1,
方程的两边都乘以(x+3)(x﹣3),得:(x+1)(x﹣3)﹣12=(x+3)(x﹣3),
去括号,得:x2﹣3x+x﹣3﹣12=x2﹣9,
移项,得:x2﹣x2﹣3x+x=﹣9+3+12,
合并同类项,得:﹣2x=6,
系数化为1,得:x=﹣3.
检验:当x=﹣3时,(x+3)(x﹣3)=0,所以x=﹣3是原方程的增根,
所以,原方程无解.
19.(2024春 福田区校级期末)解不等式组,并把解集在数轴上表示出来.
【解答】解:解不等式①,得:x≥﹣2,
解不等式②,得:x<1,
则不等式组的解集为﹣2≤x<1,
将不等式组的解集表示在数轴上如下:
20.(2024春 海沧区期末)先化简,再求值:,其中.
【解答】解:
,
当x1时,原式.
21.(2024春 蓬江区校级期末)如图,在△ABC中,点D是边BC的中点,点E在△ABC内,AE平分∠BAC,CE⊥AE,点F在边AB上,EF∥BC.
(1)求证:四边形BDEF是平行四边形;
(2)若AB=10,AC=4,求BF的长.
【解答】(1)证明:延长CE交AB于点G,
∵AE⊥CE,
∴∠AEG=∠AEC=90°,
在△AEG和△AEC中,
,
∴△AGE≌△ACE(ASA).
∴GE=EC.
∵BD=CD,
∴DE为△CGB的中位线,
∴DE∥AB.
∵EF∥BC,
∴四边形BDEF是平行四边形.
(2)解:∵四边形BDEF是平行四边形,
∴BF=DE.
∵D、E分别是BC、GC的中点,
∴BF=DEBG.
∵△AGE≌△ACE,
∴AG=AC,
∴BF(AB﹣AG)(AB﹣AC)(10﹣4)=3.
22.(2024春 博兴县期末)如图,在四边形ABCD中,∠B=90°,AB=BC=2,AD=1,CD=3.求四边形ABCD的面积.
【解答】解:连接AC,
∵∠B=90°,AB=BC=2,
∴AC=2,∠BAC=45°,
∵AD=1,CD=3,
∴AD2+AC2=12+(2)2,CD2=9,
∴AD2+AC2=CD2,
∴△ADC是直角三角形,
∴∠DAC=90°,
在Rt△ABC中,S△ABCBC AB2×2=2,
在Rt△ADC中,S△ADCAD AC1×2,
∴S四边形ABCD=S△ABC+S△ADC=2.
23.(2024春 大荔县期末)请根据函数的学习路径,对函数y1=2|x﹣3|﹣1的图象与性质进行探究,并解决相关问题.
x … 0 1 2 3 4 5 6 …
y … 5 m 1 ﹣1 1 3 n …
(1)表格中:m= 3 ,n= 5 .
(2)根据表格已有数据,描点,连线.在平面直角坐标系中画出该函数图象(可依据题意补方格).
(3)观察图象,问答问题:
①当x ≤3 时,y随x的增大而减小;
②该函数的最小值为 ﹣1 ;
③已知直线y2过点(1,3)和(4,1),直接写出当y1≤y2的x取值范围是 1≤x≤4 .
【解答】解:(1)当x=1时,m=2×|1﹣3|﹣1=3,
当x=6时,n=2×|6﹣3|﹣1=5,
故答案为:3,5;
(2)根据表中数据,描点,连线如图所示:
(3)解:①由图可知,由图可知,当x≤3时,y随x的增大而减小,
故答案为:x≤3;
②当x=3时,函数值y最小,最小值为﹣1.
故答案为:﹣1;
③∵直线y2过点(1,3)和(4,1),如图所示,
∴当y1≤y2的x取值范围是1≤x≤4,
故答案为:1≤x≤4.
24.(2023秋 舞阳县期末)阅读材料:对于非零实数a,b,若关于x的分式的值为零,则解得x1=a,x2=b.又因为(a+b),所以关于x的方程xa+b的解为x1=a,x2=b.
(1)理解应用:方程的解为:x1= 5 ,x2= ;
(2)知识迁移:若关于x的方程x7的解为x1=a,x2=b,求a2+b2的值;
(3)拓展提升:若关于x的方程k﹣x的解为x1=t+1,x2=t2+2,求k2﹣4k+4t3的值.
【解答】解:(1)∵xa+b的解为x1=a,x2=b,
∴5的解为x=5或x,
故答案为:5,;
(2)∵方程x7,
∴a+b=7,ab=3,
∴a2+b2=(a+b)2﹣2ab=49﹣6=43;
(3)方程k﹣x可化为x﹣1k﹣1,
设y=x﹣1,方程变形为yk﹣1,
∴y1 y2=6,y1+y2=k﹣1,
∴y1=x1﹣1,y2=x2﹣1,
∵x1=t+1,x2=t2+2,
∴y1=t+1﹣t=t,,
∴x﹣1=t或x﹣1=t2+1,
∴t(t2+1)=6,t+t2+1=k﹣1,
∴k=t+t2+2,t3+t=6,
k2﹣4k+4t3
=k(k﹣4)+4t3
=(t+t2+2)(t+t2﹣2)+4t3
=t4+6t3+t2﹣4
=t(t3+t)+6t3﹣4
=6t+6t3﹣4
=6(t3+t)﹣4
=6×6﹣4
=32.
25.(2024春 中牟县期末)2020年12月28日,习近平总书记在主持召开中央农村工作会议中指出:“坚持中国人的饭碗任何时候都要牢牢端在自己手中,饭碗主要装中国粮.”某粮食生产基地为了落实总书记的重要讲话精神,积极扩大粮食生产规模,计划投入一笔资金购买A型和B型两种农机具,已知1件A型农机具比1件B型农机具多0.5万元,用18万元购买A型农机具和15万元购买B型农机具的数量相同.
(1)求购买1件A型农机具和1件B型农机具各需多少钱?
(2)若该粮食生产基地计划购买A型和B型两种农机具共24件,且购买的总费用不超过66万元,购买A型农机具最多能购买多少件?
【解答】解:(1)设购买一件A型农机具需要x万元,购买一件B型农机具需要(x﹣0.5)万元,
根据题意,得.
解这个方程得x=3,
经检验,x=3是原方程的解,
x﹣0.5=2.5(万元),
所以,购买一件A型农机具需要3万元,购买一件B型农机具需要2.5万元;
(2)设购买A型农机具m件,
根据题意,得3m+2.5(24﹣m)≤66,
解这个不等式,得m≤12.
所以,最多可以购买12件A型农机具.
26.(2024春 涞源县期末)阅读理解
下列一组方程:①x3,②x5,③x7,…小明通过观察,发现了其中蕴含的规律,并顺利地求出了前三个方程的解,他的解过程如下:
由①x1+2得x=1或x=2;
由②x2+3得x=2或x=3;
由③x3+4得x=3或x=4.
(1)问题解决:请写出第四个方程,并按照小明的解题思路求出该方程的解;
(2)规律探究:若n为正整数,请写出第n个方程及其方程的解;
(3)变式拓展:若n为正整数,关于x的方程x2n﹣1的一个解是x=10,求n的值.
【解答】解:(1)由①x1+2得x=1或x=2;
由②x+x2+3得x=2或x=3;
由③x3+4得x=3或x=4,
则第四个方程为:x4+5,即x9,
由x4+5得:x=4或x=5;
(2)可得第n个方程为:x2n+1,
解得:x=n或x=n+1;
(3)将原方程变形,(x+2)n+(2n+1),
∴x+2=n或x+2=2n+1,
∴方程的解是x=n﹣2,或x=2n﹣1,
当n﹣2=10时,n=12,
当2n﹣1=10时,n=5.5,
∴n的值是12或5.5.
27.(2024春 阳谷县期末)如图1,△ABC中,∠C=90°,∠A、∠B、∠C的对边分别记为a、b、c.
实验一:
小聪和小明用八张这样的三角形纸片拼出了如图2所示的正方形.
(1)在图2中,正方形CDEF的面积可表示为 (a+b)2 ,正方形IJKL的面积可表示为 (a﹣b)2 (用含a,b的式子表示)
(2)请结合图2,用面积法说明(a+b)2,ab,(a﹣b)2三者之间的等量关系.
实验二:
小聪和小明分别用四个这样三角形纸片拼成了如图3所示的图形.他们根据面积法得到了一个关于边a、b、c的等式,整理后发现a2+b2=c2.
(3)请你用面积法证明a2+b2=c2.
【解答】解:(1)∵正方形CDEF的边长为a+b,
∴正方形CDEF的面积为(a+b)2.
∵正方形IJKL的边长为a﹣b,
∴正方形IJKL的面积为(a﹣b)2.
故答案为:(a+b)2,(a﹣b)2;
(2)由图2可以看出,正方形CDEF的面积﹣正方形IJKL的面积=4个矩形的面积.
∴(a+b)2﹣(a﹣b)2=4ab;
(3)∵S五边形BCFGI=S正方形BCED+S正方形HEFG+S△BID+S△IHG=S正方形ABIG+S△ABC+S△AGF,
∴a2+b2abab=c2abab.
∴a2+b2=c2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
