期末真题重组练习卷-2024-2025学年数学八年级下册苏科版(含详解)
文档属性
| 名称 | 期末真题重组练习卷-2024-2025学年数学八年级下册苏科版(含详解) |  | |
| 格式 | docx | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
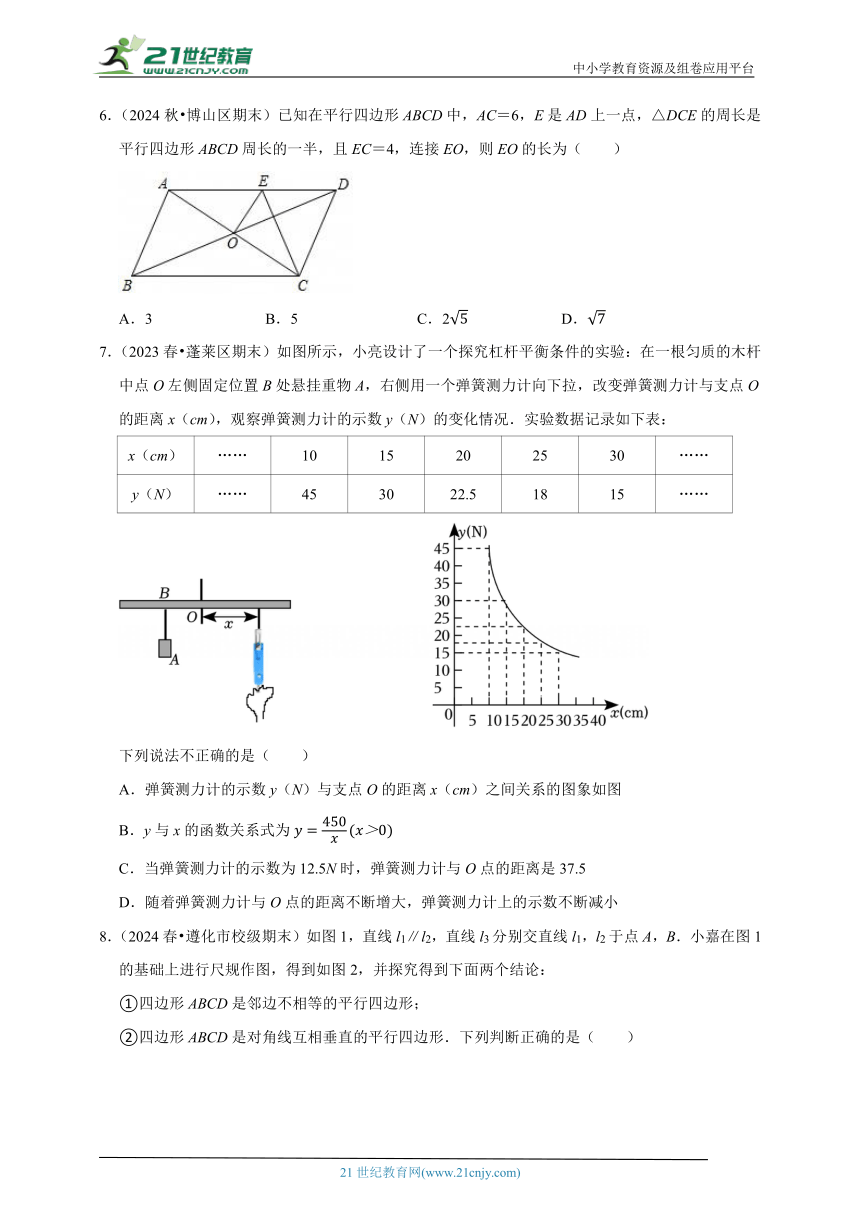
| 版本资源 | 苏科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:47:21 | ||
图片预览




文档简介
中小学教育资源及组卷应用平台
期末真题重组练习卷-2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2024秋 莱阳市期末)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(2025春 崇川区期末)下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.抛掷一枚硬币,正面向上
D.地球围绕太阳公转
3.(2014春 成都期末)分式方程解为( )
A.x=﹣4 B.x=2 C.x=﹣2 D.x=4
4.(2023春 盐田区期末)将一个边长为2cm的正方形与一个长、宽分别为4cm、1cm的矩形重叠在一起.下列图形中,重叠部分的面积最大的是( )
A. B. C. D.
5.(2024春 广饶县期末)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.2.5 B.2.4 C.1.2 D.1.3
6.(2024秋 博山区期末)已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
7.(2023春 蓬莱区期末)如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下表:
x(cm) …… 10 15 20 25 30 ……
y(N) …… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数y(N)与支点O的距离x(cm)之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
8.(2024春 遵化市校级期末)如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
二.填空题(共8小题)
9.(2025春 嘉定区期末)在菱形ABCD中,∠ABC=68°,则∠BAC= 度.
10.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: .
11.(2024秋 冷水江市期末)若2,则 .
12.(2023春 鼓楼区校级期末)如图,在△ABC中,D、E分别是AB、AC的中点,若DE=3,则BC= .
13.(2025春 虹口区校级期末)以下事件的可能性大小关系为 (由小到大写出序号).
(1)销量很大某种彩票中了一等奖;(2)掷一枚质地均匀的骰子,得到的结果为偶数;(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;(4)自然状态下水往高处流.
14.(2025春 崇川区期末)如图,在△ABC中,D、E分别为AB、BC的中点,点F在DE上,且AF⊥BF,若AB=5,AC=8,则EF的长为 .
15.(2021春 西城区校级期末)如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB,点C的坐标为(4,0),则点A的坐标为 .
16.(2022春 滕州市期末)对于实数a、b,定义一种新运算“Δ”为:aΔb,这里等式右边是实数运算例如:1Δ3.则方程xΔ(﹣3)1的解是 .
三.解答题(共11小题)
17.(2024春 渭源县期末)计算
(1);
(2)()().
18.(2025春 西安期末)解方程:.
19.(2024秋 丰城市期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
20.(2024春 仪征市期末)一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.4,估计袋中红球的个数.
21.(2024秋 博山区期末)如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
22.(2024春 灯塔市期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(﹣4,1),B(﹣1,1),C(﹣2,3).
(1)将△ABC向右平移1个单位长度,再向下平移3个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)直接写出以C1、B1、B2为顶点的三角形的形状是 .
23.(2024春 东港区校级期末)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
24.(2024秋 宣城期末)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
25.(2024春 丹阳市期末)中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式.根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.
根据图中信息回答下列问题;
(1)求接受问卷调查的学生共有 人;
(2)条形统计图中m= ,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数= °;
(3)若该校共有600名学生,根据上述调查结果,估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是多少?
26.(2022春 洪泽区期末)如图,点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500.
(1)直接写出y与x之间的函数表达式 ;
(2)若图象的另一支可以表示老李从家里出发步行到单位所需时间y(min)与速度x(m/min)之间的关系,则:
①老李家距离单位 m;
②若老李每天都七点一刻出发,单位上班时间为8点,但是员工必须提前5分钟到岗,请你用函数的性质说明老李步行速度至少为多少m/min才能不迟到?
27.(2024春 高碑店市校级期末)【规律探究题】观察下列运算:
①由,得;
②由,得;
…
问题:
(1) ; ;
(2)利用(1)中发现的规律计算:
.
期末真题重组练习卷-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D D D C C D C B
一.选择题(共8小题)
1.(2024秋 莱阳市期末)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,是中心对称图形,故此选项不合题意;
D.既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
2.(2025春 崇川区期末)下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.抛掷一枚硬币,正面向上
D.地球围绕太阳公转
【解答】解:购买一张彩票,中奖是随机事件,则A不符合题意,
打开电视,正在播放广告是随机事件,则B不符合题意,
抛掷一枚硬币,正面向上是随机事件,则C不符合题意,
地球围绕太阳公转是必然事件,则D符合题意,
故选:D.
3.(2014春 成都期末)分式方程解为( )
A.x=﹣4 B.x=2 C.x=﹣2 D.x=4
【解答】解:去分母得:x=2x﹣4,
解得:x=4,
经检验x=4是分式方程的解,
故选:D.
4.(2023春 盐田区期末)将一个边长为2cm的正方形与一个长、宽分别为4cm、1cm的矩形重叠在一起.下列图形中,重叠部分的面积最大的是( )
A. B. C. D.
【解答】解:B.S阴影=1×2=2(cm2);
C.设重叠的平行四边形的较短边为x,则较长边为,由正方形的面积=重叠部分的面积+2个小直角三角形面积,可得4=12(2﹣x),
解得x(负值已舍去),
∴S重叠部分=2x,
D.S重叠部分21;
A.图A与图C对比,因为图A的倾斜度比图C的倾斜度小,
∴图A的底比图C的底小,
∵两图为等高不等底,
∴图A阴影部分的面积小于图C阴影部分的面积;
故选:C.
5.(2024春 广饶县期末)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.2.5 B.2.4 C.1.2 D.1.3
【解答】解:如图,连接AP,
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
∵M是EF的中点,
∴PMEFAP,
根据垂线段最短可知,当AP⊥BC时,AP最短,
则PM也最短,
此时,S△ABCBC APAB AC,
∴AP2.4,
即AP最短时,AP=2.4,
∴PM的最小值AP=1.2,
故选:C.
6.(2024秋 博山区期末)已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
【解答】解:∵四边形ABCD是平行四边形,
∴AC、BD互相平分,
∴O是AC的中点.
∴OA=OCAC=3,
∵△DCE的周长是平行四边形ABCD周长的一半,
∴△DCE的周长=CD+CE+DE=CD+AD,
∴CE+DE=AD,
∵AE+DE=AD,
∴AE=CE,
∴OE是线段AC的中垂线,
∴OE⊥BD,
∵AE=EC=4,OA=3,
∴EO.
故选:D.
7.(2023春 蓬莱区期末)如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下表:
x(cm) …… 10 15 20 25 30 ……
y(N) …… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数y(N)与支点O的距离x(cm)之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
【解答】解:由图象猜测y与x之间的函数关系为反比例函数.
所以设y(k≠0),
把x=10,y=45代入求得k=450,
∴y,
将其余各点代入验证均适合,
∴y与x的函数关系式为y(x>0),
把y=12.5代入y,得x=36,
∴当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是36cm,
随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小.
故选:C.
8.(2024春 遵化市校级期末)如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
【解答】解:根据作图过程可知:AB=CB,∠ABD=∠CBD,
∵l1∥l2,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵AB=CB,
∴四边形ABCD是菱形,
∴四边形ABCD对角线互相垂直.
∴①错误,②正确.
故选B.
二.填空题(共8小题)
9.(2025春 嘉定区期末)在菱形ABCD中,∠ABC=68°,则∠BAC= 56 度.
【解答】解:如图,
∴AB=BC,
∴∠BAC=∠ACB,
由条件可知,
故答案为:56.
10.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: 3y2﹣5y﹣1=0 .
【解答】解:由题意可得:,
方程两边同乘以y,得3y2﹣1=5y,
则3y2﹣5y﹣1=0,
故答案为:3y2﹣5y﹣1=0.
11.(2024秋 冷水江市期末)若2,则 .
【解答】解:由2,得x+y=2xy
则.
故答案为.
12.(2023春 鼓楼区校级期末)如图,在△ABC中,D、E分别是AB、AC的中点,若DE=3,则BC= 6 .
【解答】解:∵D,E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵DE=3,
∴BC=2DE=6.
故答案为:6.
13.(2025春 虹口区校级期末)以下事件的可能性大小关系为 (4)(1)(2)(3) (由小到大写出序号).
(1)销量很大某种彩票中了一等奖;(2)掷一枚质地均匀的骰子,得到的结果为偶数;(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;(4)自然状态下水往高处流.
【解答】解:根据题意,将这些事件发生的可能性大小从小到大排列为:
(4)自然状态下水往高处流.
(1)销量很大某种彩票中了一等奖;
(2)掷一枚质地均匀的骰子,得到的结果为偶数;
(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;
故答案为:(4)(1)(2)(3).
14.(2025春 崇川区期末)如图,在△ABC中,D、E分别为AB、BC的中点,点F在DE上,且AF⊥BF,若AB=5,AC=8,则EF的长为 1.5 .
【解答】解:∵DE是△ABC的中位线,
∴DEBC=4.
∵AF⊥BF,D是AB的中点,
∴DFAB=2.5,
∴EF=DE﹣DF=4﹣2.5=1.5.
故答案为:1.5.
15.(2021春 西城区校级期末)如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB,点C的坐标为(4,0),则点A的坐标为 (2,1) .
【解答】解:如图,连接AB,交OC于D,
∵点C(4,0),
∴OC=4,
∵四边形AOBC是菱形,
∴ODOC4=2,AB⊥OC,
∵OB,
∴OA=OB,
在Rt△AOD中,AD1,
∴点A的坐标为(2,1).
故答案为:(2,1).
16.(2022春 滕州市期末)对于实数a、b,定义一种新运算“Δ”为:aΔb,这里等式右边是实数运算例如:1Δ3.则方程xΔ(﹣3)1的解是 x=6 .
【解答】解:xΔ(﹣3)1,
1,
1,
1=﹣2﹣(x﹣9),
解得:x=6,
检验:当x=6时,x﹣9≠0,
∴x=6是原方程的根,
故答案为:x=6.
三.解答题(共11小题)
17.(2024春 渭源县期末)计算
(1);
(2)()().
【解答】解:(1)
=32
=5;
(2)()()
=5﹣2
=3.
18.(2025春 西安期末)解方程:.
【解答】解:去分母得:2﹣x(x+1)=x2﹣1,
解得:x=1或,
检验:当x=1时,x2﹣1=0,
当x时,x2﹣1≠0,
∴分式方程的解为x.
19.(2024秋 丰城市期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
【解答】解:原式
,
∵a+2≠0,a﹣2≠0,a﹣1≠0,
∴a只能取﹣1,
当a=﹣1时,原式.
20.(2024春 仪征市期末)一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.4,估计袋中红球的个数.
【解答】解:由题意可得:摸到黑球和白球的频率之和为:1﹣0.4=0.6,
∴总的球数为:(7+5)÷0.6=20,
∴红球有:20﹣(7+5)=8(个).
21.(2024秋 博山区期末)如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
22.(2024春 灯塔市期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(﹣4,1),B(﹣1,1),C(﹣2,3).
(1)将△ABC向右平移1个单位长度,再向下平移3个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)直接写出以C1、B1、B2为顶点的三角形的形状是 等腰直角三角形 .
【解答】解:(1)如图,△A1B1C1为所作;点A1,B1,C1的坐标分别为(﹣3,﹣2),(0,﹣2),(﹣1,0)
(2)如图,△A2B2C2为所作.
(3)∵C1B12=5,C1B22=5,B1B22=10,
∴C1B12+C1B22=B1B22,C1B1=C1B2,
∴以C1、B1、B2为顶点的三角形的形状是等腰直角三角形.
故答案为等腰直角三角形.
23.(2024春 东港区校级期末)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
24.(2024秋 宣城期末)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
【解答】解:(1)把A(6,1)代入y2中,
解得:m=6,
故反比例函数的解析式为y2;
把B(a,﹣3)代入y2,解得a=﹣2,
故B(﹣2,﹣3),
把A(6,1),B(﹣2,﹣3)代入y1=kx+b,
得,解得:,
故一次函数解析式为y1x﹣2;
(2)如图,设一次函数y1x﹣2与x轴交于点C,
令y=0,得x=4.
∴点C的坐标是(4,0),
∴S△AOB=S△AOC+S△BOC4×14×3=8.
故答案为:8;
(3)由图象可知,当﹣2≤x<0或x≥6时,y1≥y2,
所以y1≥y2时x的取值范围是﹣2≤x<0或x≥6.
25.(2024春 丹阳市期末)中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式.根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.
根据图中信息回答下列问题;
(1)求接受问卷调查的学生共有 80 人;
(2)条形统计图中m= 16 ,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数= 90 °;
(3)若该校共有600名学生,根据上述调查结果,估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是多少?
【解答】解:(1)40÷50%=80(人),
∴接受问卷调查的学生共有80人,
故答案为:80;
(2)m=80﹣20﹣40﹣4=16(人);
扇形统计图中“非常了解”部分所对应扇形的圆心角=90°,
答:故答案为:16,90;
(3)600=450(名),
答:估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是450名.
26.(2022春 洪泽区期末)如图,点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500.
(1)直接写出y与x之间的函数表达式 y ;
(2)若图象的另一支可以表示老李从家里出发步行到单位所需时间y(min)与速度x(m/min)之间的关系,则:
①老李家距离单位 3000 m;
②若老李每天都七点一刻出发,单位上班时间为8点,但是员工必须提前5分钟到岗,请你用函数的性质说明老李步行速度至少为多少m/min才能不迟到?
【解答】解:(1)设y与x之间的函数表达式为y.
∵点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500,
∴|k|=1500,
∴k=±3000,
∵k>0,
∴k=3000,
∴y与x之间的函数表达式为y.
故答案为:y;
(2)①由题意可知,y,
∴老李家距离单位3000m.
故答案为:3000;
②∵y,
∴当y=60﹣15﹣5=40时,40,
解得x=75.
∵在每一个象限内,y随x的增大而减小,
∴老李步行速度至少为75m/min才能不迟到.
27.(2024春 高碑店市校级期末)【规律探究题】观察下列运算:
①由,得;
②由,得;
…
问题:
(1) ; ;
(2)利用(1)中发现的规律计算:
.
【解答】解:(1),
(n为正整数),
故答案为:;;
(2)原式=(1 ) (1)
=(1)(1)
=2025﹣1
=2024.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
期末真题重组练习卷-2024-2025学年数学八年级下册苏科版
一.选择题(共8小题)
1.(2024秋 莱阳市期末)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
2.(2025春 崇川区期末)下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.抛掷一枚硬币,正面向上
D.地球围绕太阳公转
3.(2014春 成都期末)分式方程解为( )
A.x=﹣4 B.x=2 C.x=﹣2 D.x=4
4.(2023春 盐田区期末)将一个边长为2cm的正方形与一个长、宽分别为4cm、1cm的矩形重叠在一起.下列图形中,重叠部分的面积最大的是( )
A. B. C. D.
5.(2024春 广饶县期末)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.2.5 B.2.4 C.1.2 D.1.3
6.(2024秋 博山区期末)已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
7.(2023春 蓬莱区期末)如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下表:
x(cm) …… 10 15 20 25 30 ……
y(N) …… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数y(N)与支点O的距离x(cm)之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
8.(2024春 遵化市校级期末)如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
二.填空题(共8小题)
9.(2025春 嘉定区期末)在菱形ABCD中,∠ABC=68°,则∠BAC= 度.
10.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: .
11.(2024秋 冷水江市期末)若2,则 .
12.(2023春 鼓楼区校级期末)如图,在△ABC中,D、E分别是AB、AC的中点,若DE=3,则BC= .
13.(2025春 虹口区校级期末)以下事件的可能性大小关系为 (由小到大写出序号).
(1)销量很大某种彩票中了一等奖;(2)掷一枚质地均匀的骰子,得到的结果为偶数;(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;(4)自然状态下水往高处流.
14.(2025春 崇川区期末)如图,在△ABC中,D、E分别为AB、BC的中点,点F在DE上,且AF⊥BF,若AB=5,AC=8,则EF的长为 .
15.(2021春 西城区校级期末)如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB,点C的坐标为(4,0),则点A的坐标为 .
16.(2022春 滕州市期末)对于实数a、b,定义一种新运算“Δ”为:aΔb,这里等式右边是实数运算例如:1Δ3.则方程xΔ(﹣3)1的解是 .
三.解答题(共11小题)
17.(2024春 渭源县期末)计算
(1);
(2)()().
18.(2025春 西安期末)解方程:.
19.(2024秋 丰城市期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
20.(2024春 仪征市期末)一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.4,估计袋中红球的个数.
21.(2024秋 博山区期末)如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
22.(2024春 灯塔市期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(﹣4,1),B(﹣1,1),C(﹣2,3).
(1)将△ABC向右平移1个单位长度,再向下平移3个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)直接写出以C1、B1、B2为顶点的三角形的形状是 .
23.(2024春 东港区校级期末)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
24.(2024秋 宣城期末)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
25.(2024春 丹阳市期末)中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式.根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.
根据图中信息回答下列问题;
(1)求接受问卷调查的学生共有 人;
(2)条形统计图中m= ,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数= °;
(3)若该校共有600名学生,根据上述调查结果,估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是多少?
26.(2022春 洪泽区期末)如图,点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500.
(1)直接写出y与x之间的函数表达式 ;
(2)若图象的另一支可以表示老李从家里出发步行到单位所需时间y(min)与速度x(m/min)之间的关系,则:
①老李家距离单位 m;
②若老李每天都七点一刻出发,单位上班时间为8点,但是员工必须提前5分钟到岗,请你用函数的性质说明老李步行速度至少为多少m/min才能不迟到?
27.(2024春 高碑店市校级期末)【规律探究题】观察下列运算:
①由,得;
②由,得;
…
问题:
(1) ; ;
(2)利用(1)中发现的规律计算:
.
期末真题重组练习卷-2024-2025学年数学八年级下册苏科版
参考答案与试题解析
一.选择题(共8小题)
题号 1 2 3 4 5 6 7 8
答案 D D D C C D C B
一.选择题(共8小题)
1.(2024秋 莱阳市期末)下列食品标识中,既是轴对称图形又是中心对称图形的是( )
A. B.
C. D.
【解答】解:A.不是轴对称图形,也不是中心对称图形,故此选项不合题意;
B.是轴对称图形,不是中心对称图形,故此选项不合题意;
C.不是轴对称图形,是中心对称图形,故此选项不合题意;
D.既是轴对称图形又是中心对称图形,故此选项符合题意.
故选:D.
2.(2025春 崇川区期末)下列事件中,为必然事件的是( )
A.购买一张彩票,中奖
B.打开电视,正在播放广告
C.抛掷一枚硬币,正面向上
D.地球围绕太阳公转
【解答】解:购买一张彩票,中奖是随机事件,则A不符合题意,
打开电视,正在播放广告是随机事件,则B不符合题意,
抛掷一枚硬币,正面向上是随机事件,则C不符合题意,
地球围绕太阳公转是必然事件,则D符合题意,
故选:D.
3.(2014春 成都期末)分式方程解为( )
A.x=﹣4 B.x=2 C.x=﹣2 D.x=4
【解答】解:去分母得:x=2x﹣4,
解得:x=4,
经检验x=4是分式方程的解,
故选:D.
4.(2023春 盐田区期末)将一个边长为2cm的正方形与一个长、宽分别为4cm、1cm的矩形重叠在一起.下列图形中,重叠部分的面积最大的是( )
A. B. C. D.
【解答】解:B.S阴影=1×2=2(cm2);
C.设重叠的平行四边形的较短边为x,则较长边为,由正方形的面积=重叠部分的面积+2个小直角三角形面积,可得4=12(2﹣x),
解得x(负值已舍去),
∴S重叠部分=2x,
D.S重叠部分21;
A.图A与图C对比,因为图A的倾斜度比图C的倾斜度小,
∴图A的底比图C的底小,
∵两图为等高不等底,
∴图A阴影部分的面积小于图C阴影部分的面积;
故选:C.
5.(2024春 广饶县期末)如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
A.2.5 B.2.4 C.1.2 D.1.3
【解答】解:如图,连接AP,
∵∠BAC=90°,AB=3,AC=4,
∴BC5,
∵PE⊥AB,PF⊥AC,
∴∠AEP=∠AFP=90°,
∴四边形AFPE是矩形,
∴EF=AP,
∵M是EF的中点,
∴PMEFAP,
根据垂线段最短可知,当AP⊥BC时,AP最短,
则PM也最短,
此时,S△ABCBC APAB AC,
∴AP2.4,
即AP最短时,AP=2.4,
∴PM的最小值AP=1.2,
故选:C.
6.(2024秋 博山区期末)已知在平行四边形ABCD中,AC=6,E是AD上一点,△DCE的周长是平行四边形ABCD周长的一半,且EC=4,连接EO,则EO的长为( )
A.3 B.5 C.2 D.
【解答】解:∵四边形ABCD是平行四边形,
∴AC、BD互相平分,
∴O是AC的中点.
∴OA=OCAC=3,
∵△DCE的周长是平行四边形ABCD周长的一半,
∴△DCE的周长=CD+CE+DE=CD+AD,
∴CE+DE=AD,
∵AE+DE=AD,
∴AE=CE,
∴OE是线段AC的中垂线,
∴OE⊥BD,
∵AE=EC=4,OA=3,
∴EO.
故选:D.
7.(2023春 蓬莱区期末)如图所示,小亮设计了一个探究杠杆平衡条件的实验:在一根匀质的木杆中点O左侧固定位置B处悬挂重物A,右侧用一个弹簧测力计向下拉,改变弹簧测力计与支点O的距离x(cm),观察弹簧测力计的示数y(N)的变化情况.实验数据记录如下表:
x(cm) …… 10 15 20 25 30 ……
y(N) …… 45 30 22.5 18 15 ……
下列说法不正确的是( )
A.弹簧测力计的示数y(N)与支点O的距离x(cm)之间关系的图象如图
B.y与x的函数关系式为
C.当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是37.5
D.随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小
【解答】解:由图象猜测y与x之间的函数关系为反比例函数.
所以设y(k≠0),
把x=10,y=45代入求得k=450,
∴y,
将其余各点代入验证均适合,
∴y与x的函数关系式为y(x>0),
把y=12.5代入y,得x=36,
∴当弹簧测力计的示数为12.5N时,弹簧测力计与O点的距离是36cm,
随着弹簧测力计与O点的距离不断增大,弹簧测力计上的示数不断减小.
故选:C.
8.(2024春 遵化市校级期末)如图1,直线l1∥l2,直线l3分别交直线l1,l2于点A,B.小嘉在图1的基础上进行尺规作图,得到如图2,并探究得到下面两个结论:
①四边形ABCD是邻边不相等的平行四边形;
②四边形ABCD是对角线互相垂直的平行四边形.下列判断正确的是( )
A.①②都正确 B.①错误,②正确
C.①②都错误 D.①正确,②错误
【解答】解:根据作图过程可知:AB=CB,∠ABD=∠CBD,
∵l1∥l2,
∴∠ADB=∠CBD,
∴∠ABD=∠ADB,
∴AB=AD,
∴AD=BC,
∴四边形ABCD是平行四边形,
∵AB=CB,
∴四边形ABCD是菱形,
∴四边形ABCD对角线互相垂直.
∴①错误,②正确.
故选B.
二.填空题(共8小题)
9.(2025春 嘉定区期末)在菱形ABCD中,∠ABC=68°,则∠BAC= 56 度.
【解答】解:如图,
∴AB=BC,
∴∠BAC=∠ACB,
由条件可知,
故答案为:56.
10.(2025春 嘉定区期末)解方程时,可以设,那么原方程可转化为整式方程: 3y2﹣5y﹣1=0 .
【解答】解:由题意可得:,
方程两边同乘以y,得3y2﹣1=5y,
则3y2﹣5y﹣1=0,
故答案为:3y2﹣5y﹣1=0.
11.(2024秋 冷水江市期末)若2,则 .
【解答】解:由2,得x+y=2xy
则.
故答案为.
12.(2023春 鼓楼区校级期末)如图,在△ABC中,D、E分别是AB、AC的中点,若DE=3,则BC= 6 .
【解答】解:∵D,E分别是△ABC的边AB和AC的中点,
∴DE是△ABC的中位线,
∵DE=3,
∴BC=2DE=6.
故答案为:6.
13.(2025春 虹口区校级期末)以下事件的可能性大小关系为 (4)(1)(2)(3) (由小到大写出序号).
(1)销量很大某种彩票中了一等奖;(2)掷一枚质地均匀的骰子,得到的结果为偶数;(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;(4)自然状态下水往高处流.
【解答】解:根据题意,将这些事件发生的可能性大小从小到大排列为:
(4)自然状态下水往高处流.
(1)销量很大某种彩票中了一等奖;
(2)掷一枚质地均匀的骰子,得到的结果为偶数;
(3)4个球随机放入3个盒子中,至少有一个盒子中的球数不少于2个;
故答案为:(4)(1)(2)(3).
14.(2025春 崇川区期末)如图,在△ABC中,D、E分别为AB、BC的中点,点F在DE上,且AF⊥BF,若AB=5,AC=8,则EF的长为 1.5 .
【解答】解:∵DE是△ABC的中位线,
∴DEBC=4.
∵AF⊥BF,D是AB的中点,
∴DFAB=2.5,
∴EF=DE﹣DF=4﹣2.5=1.5.
故答案为:1.5.
15.(2021春 西城区校级期末)如图,以菱形AOBC的顶点O为原点,对角线OC所在直线为x轴建立平面直角坐标系,若OB,点C的坐标为(4,0),则点A的坐标为 (2,1) .
【解答】解:如图,连接AB,交OC于D,
∵点C(4,0),
∴OC=4,
∵四边形AOBC是菱形,
∴ODOC4=2,AB⊥OC,
∵OB,
∴OA=OB,
在Rt△AOD中,AD1,
∴点A的坐标为(2,1).
故答案为:(2,1).
16.(2022春 滕州市期末)对于实数a、b,定义一种新运算“Δ”为:aΔb,这里等式右边是实数运算例如:1Δ3.则方程xΔ(﹣3)1的解是 x=6 .
【解答】解:xΔ(﹣3)1,
1,
1,
1=﹣2﹣(x﹣9),
解得:x=6,
检验:当x=6时,x﹣9≠0,
∴x=6是原方程的根,
故答案为:x=6.
三.解答题(共11小题)
17.(2024春 渭源县期末)计算
(1);
(2)()().
【解答】解:(1)
=32
=5;
(2)()()
=5﹣2
=3.
18.(2025春 西安期末)解方程:.
【解答】解:去分母得:2﹣x(x+1)=x2﹣1,
解得:x=1或,
检验:当x=1时,x2﹣1=0,
当x时,x2﹣1≠0,
∴分式方程的解为x.
19.(2024秋 丰城市期末)先化简代数式,再从2,﹣2,1,﹣1四个数中选择一个你喜欢的数代入求值.
【解答】解:原式
,
∵a+2≠0,a﹣2≠0,a﹣1≠0,
∴a只能取﹣1,
当a=﹣1时,原式.
20.(2024春 仪征市期末)一个不透明的布袋中装有除颜色外均相同的7个黑球、5个白球和若干个红球.每次摇匀后随机摸出一个球,记下颜色后再放回袋中,通过大量重复摸球试验后,发现摸到红球的频率稳定在0.4,估计袋中红球的个数.
【解答】解:由题意可得:摸到黑球和白球的频率之和为:1﹣0.4=0.6,
∴总的球数为:(7+5)÷0.6=20,
∴红球有:20﹣(7+5)=8(个).
21.(2024秋 博山区期末)如图,等边△ABC的边长是4,D,E分别为AB,AC的中点,延长BC至点F,使CFBC,连接CD和EF.
(1)求证:DE=CF;
(2)求EF的长;
(3)求四边形DEFC的面积.
【解答】解:(1)在△ABC中,
∵D、E分别为AB、AC的中点,
∴DE为△ABC的中位线,
∴DEBC,
∵CFBC,
∴DE=CF.
(2)∵AC=BC,AD=BD,
∴CD⊥AB,
∵BC=4,BD=2,
∴CD2,
∵DE∥CF,DE=CF,
∴四边形DEFC是平行四边形,
∴EF=CD=2.
(3)过点D作DH⊥BC于H.
∵∠DHC=90°,∠DCB=30°,
∴DHDC,
∵DE=CF=2,
∴S四边形DEFC=CF DH=22.
22.(2024春 灯塔市期末)如图,正方形网格中,每个小正方形的边长都是一个单位长度,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(﹣4,1),B(﹣1,1),C(﹣2,3).
(1)将△ABC向右平移1个单位长度,再向下平移3个单位长度后得到△A1B1C1,请画出△A1B1C1;
(2)将△ABC绕原点O顺时针旋转90°后得到△A2B2C2,请画出△A2B2C2;
(3)直接写出以C1、B1、B2为顶点的三角形的形状是 等腰直角三角形 .
【解答】解:(1)如图,△A1B1C1为所作;点A1,B1,C1的坐标分别为(﹣3,﹣2),(0,﹣2),(﹣1,0)
(2)如图,△A2B2C2为所作.
(3)∵C1B12=5,C1B22=5,B1B22=10,
∴C1B12+C1B22=B1B22,C1B1=C1B2,
∴以C1、B1、B2为顶点的三角形的形状是等腰直角三角形.
故答案为等腰直角三角形.
23.(2024春 东港区校级期末)如图,在四边形ABCD中,AB∥DC,AB=AD,对角线AC,BD交于点O,AC平分∠BAD,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若,BD=2,求OE的长.
【解答】(1)证明:∵AB∥DC,
∴∠OAB=∠DCA,
∵AC为∠DAB的平分线,
∴∠OAB=∠DAC,
∴∠DCA=∠DAC,
∴CD=AD=AB,
∵AB∥DC,
∴四边形ABCD是平行四边形,
∵AD=AB,
∴平行四边形ABCD是菱形;
(2)解:∵四边形ABCD是菱形,
∴OA=OC,BD⊥AC,
∵CE⊥AB,
∴OE=OA=OC,
∵BD=2,
∴,
在Rt△AOB中,,OB=1,
∴,
∴OE=OA=2.
24.(2024秋 宣城期末)如图,已知一次函数y1=kx+b与反比例函数的图象在第一、三象限分别交于A(6,1),B(a,﹣3)两点,连接OA,OB.
(1)求一次函数和反比例函数的解析式;
(2)求△AOB的面积;
(3)直接写出y1≥y2时x的取值范围.
【解答】解:(1)把A(6,1)代入y2中,
解得:m=6,
故反比例函数的解析式为y2;
把B(a,﹣3)代入y2,解得a=﹣2,
故B(﹣2,﹣3),
把A(6,1),B(﹣2,﹣3)代入y1=kx+b,
得,解得:,
故一次函数解析式为y1x﹣2;
(2)如图,设一次函数y1x﹣2与x轴交于点C,
令y=0,得x=4.
∴点C的坐标是(4,0),
∴S△AOB=S△AOC+S△BOC4×14×3=8.
故答案为:8;
(3)由图象可知,当﹣2≤x<0或x≥6时,y1≥y2,
所以y1≥y2时x的取值范围是﹣2≤x<0或x≥6.
25.(2024春 丹阳市期末)中学生心理健康受到社会的广泛关注,某校开展心理健康教育专题讲座,就学生对心理健康知识的了解程度,采用随机抽样调查的方式.根据收集到的信息进行统计,绘制了如图所示的两幅尚不完整的统计图.
根据图中信息回答下列问题;
(1)求接受问卷调查的学生共有 80 人;
(2)条形统计图中m= 16 ,扇形统计图中“非常了解”部分所对应扇形的圆心角的度数= 90 °;
(3)若该校共有600名学生,根据上述调查结果,估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是多少?
【解答】解:(1)40÷50%=80(人),
∴接受问卷调查的学生共有80人,
故答案为:80;
(2)m=80﹣20﹣40﹣4=16(人);
扇形统计图中“非常了解”部分所对应扇形的圆心角=90°,
答:故答案为:16,90;
(3)600=450(名),
答:估计学校全体学生通过专题讲座对心理健康知识的了解程度至少达到“基本了解”的程度的人数是450名.
26.(2022春 洪泽区期末)如图,点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500.
(1)直接写出y与x之间的函数表达式 y ;
(2)若图象的另一支可以表示老李从家里出发步行到单位所需时间y(min)与速度x(m/min)之间的关系,则:
①老李家距离单位 3000 m;
②若老李每天都七点一刻出发,单位上班时间为8点,但是员工必须提前5分钟到岗,请你用函数的性质说明老李步行速度至少为多少m/min才能不迟到?
【解答】解:(1)设y与x之间的函数表达式为y.
∵点A是反比例函数图象上的一点,AB⊥x轴,垂足为B,三角形ABO面积为1500,
∴|k|=1500,
∴k=±3000,
∵k>0,
∴k=3000,
∴y与x之间的函数表达式为y.
故答案为:y;
(2)①由题意可知,y,
∴老李家距离单位3000m.
故答案为:3000;
②∵y,
∴当y=60﹣15﹣5=40时,40,
解得x=75.
∵在每一个象限内,y随x的增大而减小,
∴老李步行速度至少为75m/min才能不迟到.
27.(2024春 高碑店市校级期末)【规律探究题】观察下列运算:
①由,得;
②由,得;
…
问题:
(1) ; ;
(2)利用(1)中发现的规律计算:
.
【解答】解:(1),
(n为正整数),
故答案为:;;
(2)原式=(1 ) (1)
=(1)(1)
=2025﹣1
=2024.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
21世纪教育网(www.21cnjy.com)
同课章节目录
