第六单元平行四边形和梯形期末复习练(含解析)西师大版数学四年级下册
文档属性
| 名称 | 第六单元平行四边形和梯形期末复习练(含解析)西师大版数学四年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 181.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 西师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 00:00:00 | ||
图片预览

文档简介
第六单元平行四边形和梯形
学校:___________姓名:___________班级:___________考号:___________
一、选择题
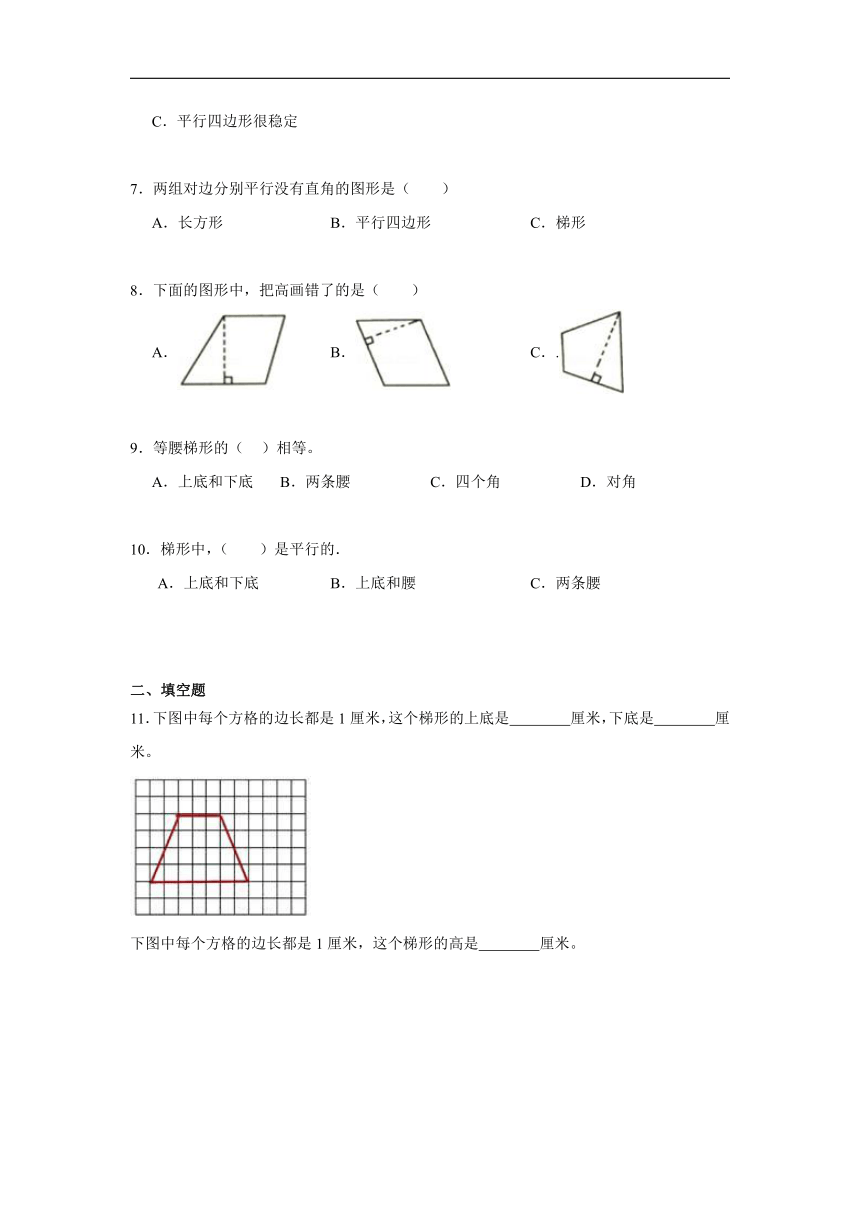
1.如图:小明和小林都从学校出发到书店买书,他们走的路程比较,( )
A.小明走的路程多 B.小林走的路程多 C.一样多
2.把一个边长15分米的正方形木条框拉成一个平行四边形,这个平行四边形的周长是( )米。
A.60 B.6 C.不能确定
3.易变形的图形是( )。
A.平行四边形 B.三角形 C.等腰三角形
4.下列梯形高的画法正确的是( )
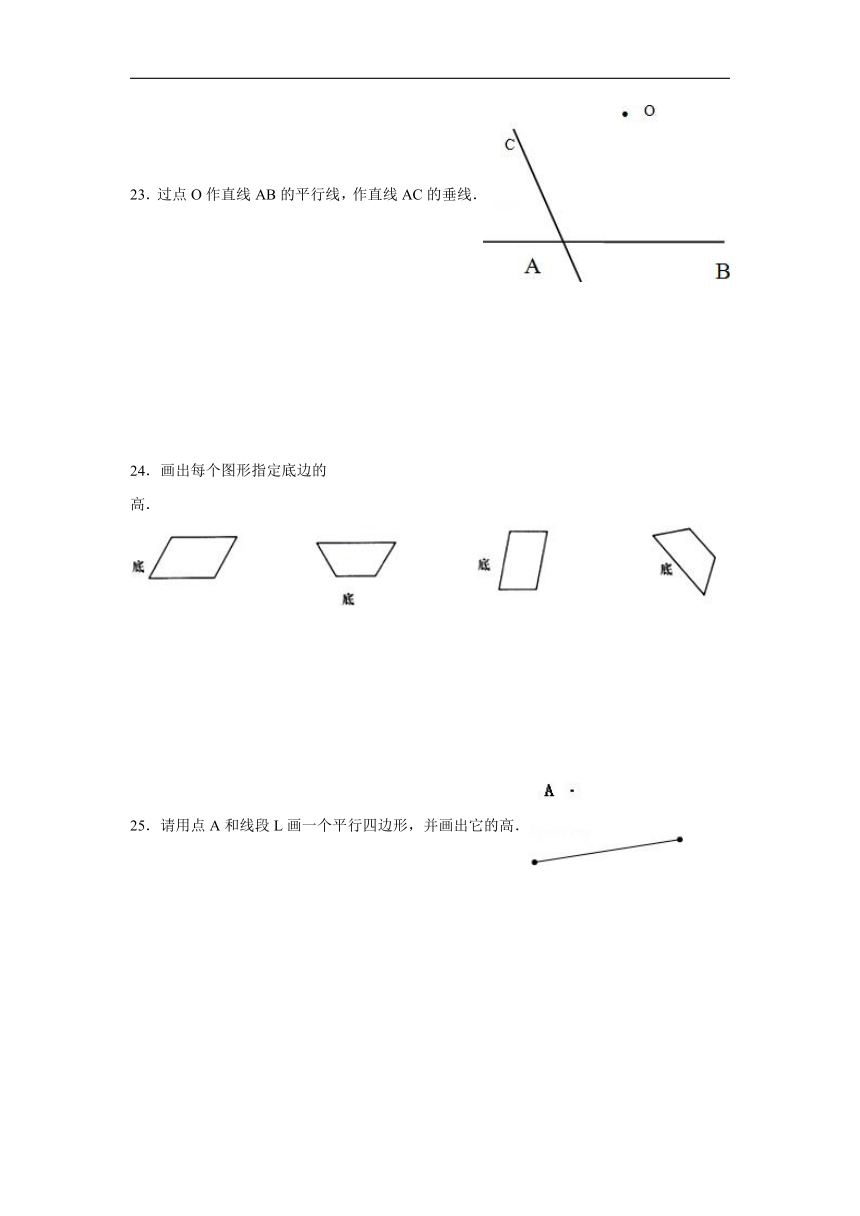
A. B. C.
5.如图中,( )不是平行四边形
A. B. C.
6.下面关于平行四边形的说法中,不正确的是( ).
A.对边相等
B.平行四边形的两组对边分别平行
C.平行四边形很稳定
7.两组对边分别平行没有直角的图形是( )
A.长方形 B.平行四边形 C.梯形
8.下面的图形中,把高画错了的是( )
A. B. C..
9.等腰梯形的( )相等。
A.上底和下底 B.两条腰 C.四个角 D.对角
10.梯形中,( )是平行的.
A.上底和下底 B.上底和腰 C.两条腰
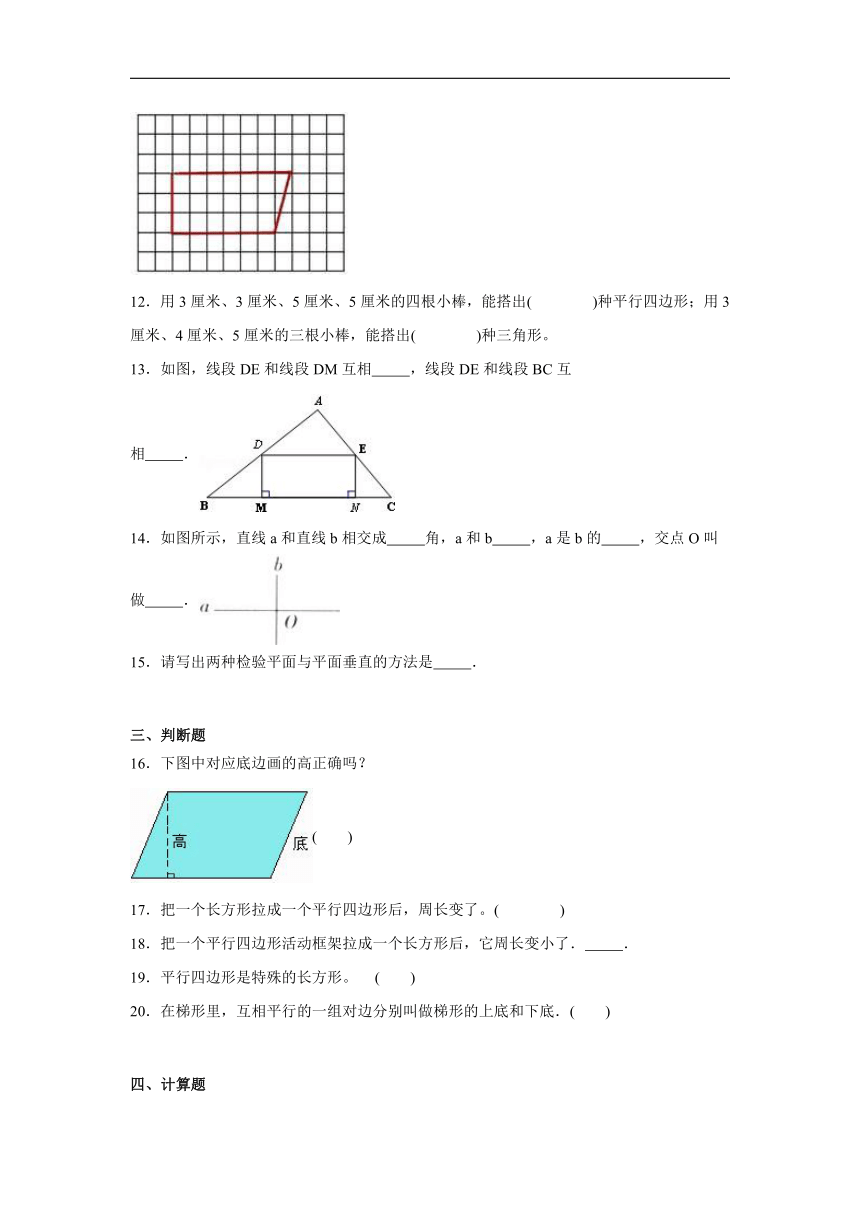
二、填空题
11.下图中每个方格的边长都是1厘米,这个梯形的上底是 厘米,下底是 厘米。
下图中每个方格的边长都是1厘米,这个梯形的高是 厘米。
12.用3厘米、3厘米、5厘米、5厘米的四根小棒,能搭出( )种平行四边形;用3厘米、4厘米、5厘米的三根小棒,能搭出( )种三角形。
13.如图,线段DE和线段DM互相 ,线段DE和线段BC互相 .
14.如图所示,直线a和直线b相交成 角,a和b ,a是b的 ,交点O叫做 .
15.请写出两种检验平面与平面垂直的方法是 .
三、判断题
16.下图中对应底边画的高正确吗?
( )
17.把一个长方形拉成一个平行四边形后,周长变了。( )
18.把一个平行四边形活动框架拉成一个长方形后,它周长变小了. .
19.平行四边形是特殊的长方形。 ( )
20.在梯形里,互相平行的一组对边分别叫做梯形的上底和下底.( )
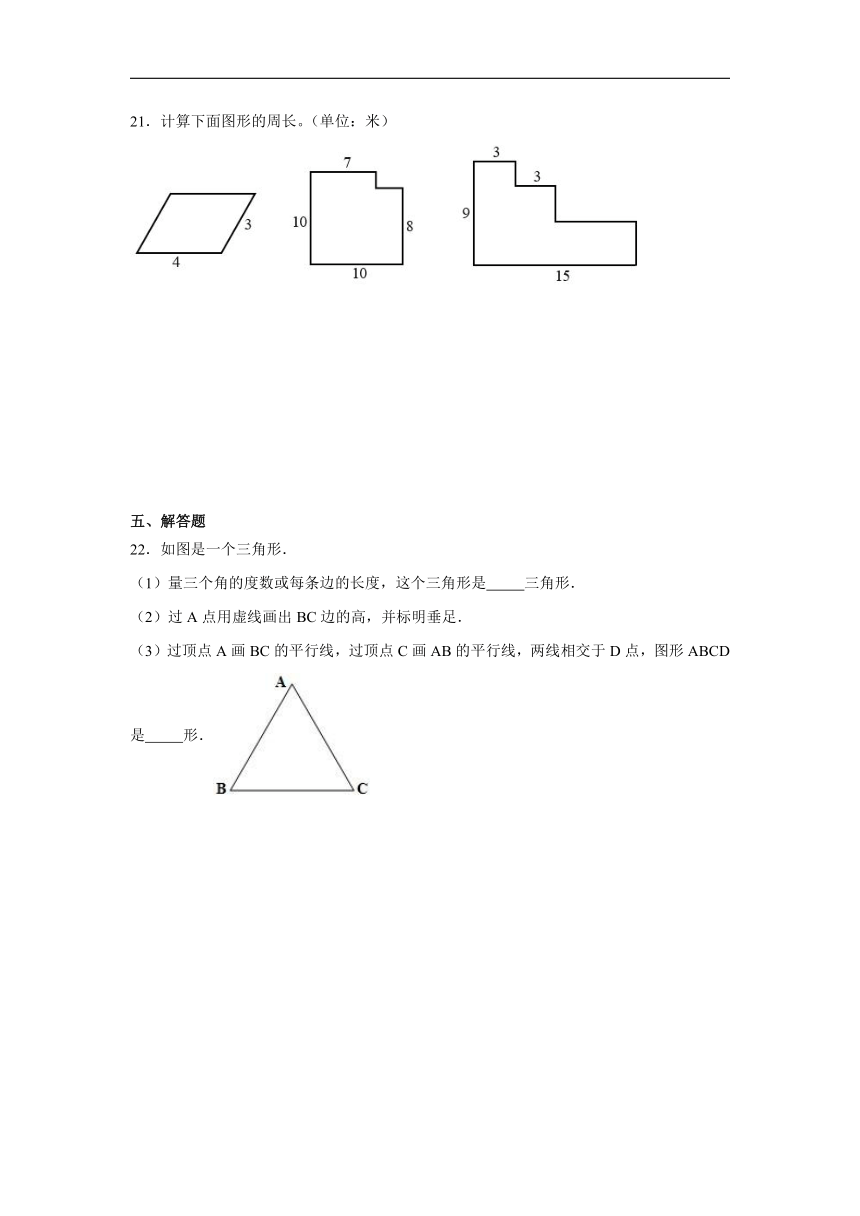
四、计算题
21.计算下面图形的周长。(单位:米)
五、解答题
22.如图是一个三角形.
(1)量三个角的度数或每条边的长度,这个三角形是 三角形.
(2)过A点用虚线画出BC边的高,并标明垂足.
(3)过顶点A画BC的平行线,过顶点C画AB的平行线,两线相交于D点,图形ABCD是 形.
23.过点O作直线AB的平行线,作直线AC的垂线.
24.画出每个图形指定底边的高.
25.请用点A和线段L画一个平行四边形,并画出它的高.
《第六单元平行四边形和梯形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A B C C B C B A
1.C
【详解】因为平行四边形的对边相等,所以小明和小林都从学校出发到书店买书,他们走的路程一样多
2.B
【分析】把一个边长15分米的正方形木条框拉成一个平行四边形,此时平行四边形的周长=正方形的周长,平行四边形的底=平行四边形的腰=正方形的边长,正方形的周长=边长×4。
【详解】把一个边长15分米的正方形木条框拉成一个平行四边形,此时平行四边形的周长=正方形的周长=15×4=60分米=6米。
故答案为:B
3.A
【分析】根据平行四边形的不稳定性的特点进行解答即可。
【详解】因为平行四边形具有不稳定性,所以平行四边形最易变形。
故答案为:A
4.B
【详解】略
5.C
【详解】图A、图B符合平行四边形对边平行且相等的特点,所以这两个图形是平行四边形,图C不符合平行四边形对边平行且相等的特点.
6.C
【详解】略
7.B
【详解】平行四边形的含义:两组对边分别平行的四边形是平行四边形;如果两组对边分别平行、有4个直角的四边形是长方形或正方形;
故选B.
8.C
【详解】试题分析:根据平行四边形的高的意义,从平行四边形固定的底的对边上任意一点向它画垂线段,这条垂线就叫高;
在梯形中,从一底的任一点作另一底的垂线,这点与垂足间的距离叫做梯形的高.习惯上作梯形的高时都从上底(较短的底)一个顶点出发作下底的垂线,由此判断即可.
解:根据题干分析,A,B作图正确;
C不是梯形两底之间的垂线,不正确.
故选C.
点评:此题主要根据平行四边形和梯形的高的意义和画垂线的方法解决问题,注意作高必须在底边上画出垂直的标志.
9.B
【分析】等腰梯形同一底上的两个角相等;等腰梯形的两条腰相等,由此解答即可。
【详解】根据分析可知,等腰梯形的两条腰相等。
故答案为:B
【点睛】本题考查等腰梯形的性质,属于基础题,需熟练掌握。
10.A
【分析】本题是考查梯形的特征,在梯形中平行的两边叫做梯形的底,习惯上把较短的底叫上底,较长的底叫下底.
【详解】根据梯形的意义,一组对边平行,另一组对边不平行的四边形是梯形(一组对边平行且不相等的四边形是梯形),平行的两边叫梯形的底.所以在梯形中,互相平行的一组对边叫做梯形的上底和下底;
故选A.
11. 3 7 3
【详解】略
12. 无数 1
【分析】平行四边形具有易变形性。用这四根小棒搭出一个平行四边形后,拽住一个角拉伸,可以得到无数个平行四边形,这些平行四边形的四条边相同,但内角不同。三角形具有稳定性。用这三根小棒搭出一个三角形后,这个三角形很稳定,不能在拉伸过程中得到其余的三角形,也就是只能搭出一个三角形。
【详解】用3厘米、3厘米、5厘米、5厘米的四根小棒,能搭出无数种平行四边形;用3厘米、4厘米、5厘米的三根小棒,能搭出1种三角形。
【点睛】本题关键是明确平行四边形具有易变形性,三角形具有稳定性。
13.垂直,平行
【详解】试题分析:由图可知:四边形DENM是长方形,则四个角都是直角,并且两组对边分别平行且相等;据此解答即可.
解:由分析可知:∠EDM=90°,即线段DE和线段DM互相垂直;
因为四边形DENM是长方形,即DE∥MN,则DE∥BC,
所以线段DE和线段BC互相平行;
故答案为垂直,平行.
点评:解答此题的关键:认真看图,根据长方形的特征及性质进行解答.
14.直,互相垂直,垂线,垂足
【详解】试题分析:根据垂直的含义:在同一平面内相交成直角的两条直线叫做互相垂直,其中一条直线叫作另一条直线的垂线;据此解答.
解:如图所示,直线a和直线b相交成直角,a和b互相垂直,a是b的垂线,交点O叫做垂足;
故答案为直,互相垂直,垂线,垂足.
点评:明确垂直的含义,是解答此题的关键.
15.(1)两把三角尺相交放置,如果两把三角尺各有一条边紧贴面,且另一条直角边都能紧贴另一平面,则平面与平面垂直.
(2)如果铅垂线与待测的平面紧贴,那么待测的平面与水平面垂直;
【详解】试题分析:只要两个平面中的一个直线与另下平面与它相交的直线垂直,那么这两个平面就相互垂直.据此解答.
解:根据分析知:
(1)两把三角尺相交放置,如果两把三角尺各有一条边紧贴面,且另一条直角边都能紧贴另一平面,则平面与平面垂直.
(2)如果铅垂线与待测的平面紧贴,那么待测的平面与水平面垂直;
点评:本题的关键是检验两个平面内相交的两条直线是否垂直.
16.错误
【分析】平行四边形有两组对边分别平行,做高时要弄清楚底和高应该相对应.
【详解】这种画高的方法是错误的,正确的如下图所示:
根据平行四边形高的概念:从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫平行四边形的高,那么平行四边形的底和高是相对应的,所以原题的画法是错误的.
故答案为错误.
17.×
【分析】平行四边形和长方形的周长就是围成它们的所有的线段的和,将长方形框架拉成一个平行四边形后,每条线段长度没有变化,所以周长不变;据此判断即可。
【详解】因为把一个长方形拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;所以原题的说法错误。
故答案为:×
【点睛】解答此题的关键是明确四边形的形状虽然发生了变化,但四条边的长度没有变化,周长就不发生变化。
18.×
【分析】根据平行四边形活动框架拉成长方形后各条边的变化来进行判断.
【详解】平行四边形活动框架拉成长方形之后,每条边的长度不变,所以周长不变.
19.×
【分析】要正确辨识长方形和平行四边形。
【详解】长方形是特殊的平行四边形。
【点睛】考查了长方形和平行四边形的定义。
20.√
【详解】只有一组对边互相平行的四边形叫梯形,在梯形里,互相平行的一组对边分别叫做梯形的上底和下底,此题说法正确.
故答案为正确.
21.14米;40米;48米
【分析】(1)平行四边形的周长等于相邻两条边的长度和的2倍,则平行四边形的周长是(4+3)×2米。
(2)
将图形的边平移后,可知图形的周长等于边长为10米的正方形的周长,根据正方形的周长=边长×4解答。
(3)
将图形的边平移后,可知图形的周长等于长15米宽9米的长方形的周长,根据长方形的周长=(长+宽)×2解答。
【详解】(1)(4+3)×2
=7×2
=14(米)
平行四边形的周长是14米。
(2)10×4=40(米)
图形的周长是40米。
(3)(15+9)×2
=24×2
=48(米)
图形的周长是48米。
22.(1)如图(1)通过测量可知三角形三条边的长度都是5cm,所以这个三角形是等边三角形.
(2)如图(2).
(3)如图(3),因为AD∥BC,AB∥CD,所以图形ABCD是平行四边形.
故答案为:等边;平行四边.
【详解】试题分析:(1)量三个角的度数或每条边的长度,根据三角形的分类可作出判断.
(2)根据高的做法画图即可解答.
(3)根据要求先画图,再根据平行四边形的性质可作出判断.
解:(1)如图(1)通过测量可知三角形三条边的长度都是5cm,所以这个三角形是等边三角形.
(2)如图(2).
(3)如图(3),因为AD∥BC,AB∥CD,所以图形ABCD是平行四边形.
故答案为等边;平行四边.
点评:本题主要考查等边三角形与平行四边形的定义,三条边或三个内角都相等的三角形为等边三角形,两组对边分别平行的四边形为平行四边形.
23.
【详解】试题分析:(1)用三角板的一条直角边的已知直线AC重合,沿重合的直线AC平移三角板,使三角板的另一条直角边和O点重合,过O沿直角边向已知AC直线画直线即可.
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线AB重合的直角边和O点重合,过O点沿三角板的直角边画直线即可.据此解答.
解:根据分析画图如下:
点评:本题主要考查了学生画垂线和平行线的能力.
24.
【详解】试题分析:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高,平行四边形有无数条高,习惯上作平行四边形的高时都从一个顶点出发作一边的垂线,用三角板的直角可以画出平行四形的高;梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
解:作平行四边形、梯形的高如下:
故答案为
点评:本题是考查作平行四边形、梯形的高.注意作高用虚线,并标出垂足.
25.
【详解】试题分析:如图,根据平行四边形的特征,对边平行且相等,连接点A和线段的一个端点B,过线段的另一个端点C作CD∥AB,且CD=AB,连接AD就是用点A和线段L画一个平行四边形,或连接AB,过点A作AD∥BC,且AD=BC,连接CD就是用点A和线段L画一个平行四边形;经过平行四边形底上的一个顶点用三角板的直角边向另一底作垂线,顶点和垂足之间的线段就是平行四边形的一条高,平行四边形有无数条高,习惯上作平行四边形的高时,都从一个顶点出发向底作垂线.
解:由分析作图如下:
点评:本题主要是考查画平行四边形及作平行四边形的高.画平行四边形时,要根据平行四边形的特征画.
26.错误
【详解】试题分析:根据平行线的定义:在同一平面内,不相交的两条直线叫平行线,即可判断.
解:因为本题说的不是直线,所以说是平行线,说法错误;
故答案为×.
点评:此题主要考查了平行线的定义,关键是注意两点:①在同一平面内②不相交的两条直线.
学校:___________姓名:___________班级:___________考号:___________
一、选择题
1.如图:小明和小林都从学校出发到书店买书,他们走的路程比较,( )
A.小明走的路程多 B.小林走的路程多 C.一样多
2.把一个边长15分米的正方形木条框拉成一个平行四边形,这个平行四边形的周长是( )米。
A.60 B.6 C.不能确定
3.易变形的图形是( )。
A.平行四边形 B.三角形 C.等腰三角形
4.下列梯形高的画法正确的是( )
A. B. C.
5.如图中,( )不是平行四边形
A. B. C.
6.下面关于平行四边形的说法中,不正确的是( ).
A.对边相等
B.平行四边形的两组对边分别平行
C.平行四边形很稳定
7.两组对边分别平行没有直角的图形是( )
A.长方形 B.平行四边形 C.梯形
8.下面的图形中,把高画错了的是( )
A. B. C..
9.等腰梯形的( )相等。
A.上底和下底 B.两条腰 C.四个角 D.对角
10.梯形中,( )是平行的.
A.上底和下底 B.上底和腰 C.两条腰
二、填空题
11.下图中每个方格的边长都是1厘米,这个梯形的上底是 厘米,下底是 厘米。
下图中每个方格的边长都是1厘米,这个梯形的高是 厘米。
12.用3厘米、3厘米、5厘米、5厘米的四根小棒,能搭出( )种平行四边形;用3厘米、4厘米、5厘米的三根小棒,能搭出( )种三角形。
13.如图,线段DE和线段DM互相 ,线段DE和线段BC互相 .
14.如图所示,直线a和直线b相交成 角,a和b ,a是b的 ,交点O叫做 .
15.请写出两种检验平面与平面垂直的方法是 .
三、判断题
16.下图中对应底边画的高正确吗?
( )
17.把一个长方形拉成一个平行四边形后,周长变了。( )
18.把一个平行四边形活动框架拉成一个长方形后,它周长变小了. .
19.平行四边形是特殊的长方形。 ( )
20.在梯形里,互相平行的一组对边分别叫做梯形的上底和下底.( )
四、计算题
21.计算下面图形的周长。(单位:米)
五、解答题
22.如图是一个三角形.
(1)量三个角的度数或每条边的长度,这个三角形是 三角形.
(2)过A点用虚线画出BC边的高,并标明垂足.
(3)过顶点A画BC的平行线,过顶点C画AB的平行线,两线相交于D点,图形ABCD是 形.
23.过点O作直线AB的平行线,作直线AC的垂线.
24.画出每个图形指定底边的高.
25.请用点A和线段L画一个平行四边形,并画出它的高.
《第六单元平行四边形和梯形》参考答案
题号 1 2 3 4 5 6 7 8 9 10
答案 C B A B C C B C B A
1.C
【详解】因为平行四边形的对边相等,所以小明和小林都从学校出发到书店买书,他们走的路程一样多
2.B
【分析】把一个边长15分米的正方形木条框拉成一个平行四边形,此时平行四边形的周长=正方形的周长,平行四边形的底=平行四边形的腰=正方形的边长,正方形的周长=边长×4。
【详解】把一个边长15分米的正方形木条框拉成一个平行四边形,此时平行四边形的周长=正方形的周长=15×4=60分米=6米。
故答案为:B
3.A
【分析】根据平行四边形的不稳定性的特点进行解答即可。
【详解】因为平行四边形具有不稳定性,所以平行四边形最易变形。
故答案为:A
4.B
【详解】略
5.C
【详解】图A、图B符合平行四边形对边平行且相等的特点,所以这两个图形是平行四边形,图C不符合平行四边形对边平行且相等的特点.
6.C
【详解】略
7.B
【详解】平行四边形的含义:两组对边分别平行的四边形是平行四边形;如果两组对边分别平行、有4个直角的四边形是长方形或正方形;
故选B.
8.C
【详解】试题分析:根据平行四边形的高的意义,从平行四边形固定的底的对边上任意一点向它画垂线段,这条垂线就叫高;
在梯形中,从一底的任一点作另一底的垂线,这点与垂足间的距离叫做梯形的高.习惯上作梯形的高时都从上底(较短的底)一个顶点出发作下底的垂线,由此判断即可.
解:根据题干分析,A,B作图正确;
C不是梯形两底之间的垂线,不正确.
故选C.
点评:此题主要根据平行四边形和梯形的高的意义和画垂线的方法解决问题,注意作高必须在底边上画出垂直的标志.
9.B
【分析】等腰梯形同一底上的两个角相等;等腰梯形的两条腰相等,由此解答即可。
【详解】根据分析可知,等腰梯形的两条腰相等。
故答案为:B
【点睛】本题考查等腰梯形的性质,属于基础题,需熟练掌握。
10.A
【分析】本题是考查梯形的特征,在梯形中平行的两边叫做梯形的底,习惯上把较短的底叫上底,较长的底叫下底.
【详解】根据梯形的意义,一组对边平行,另一组对边不平行的四边形是梯形(一组对边平行且不相等的四边形是梯形),平行的两边叫梯形的底.所以在梯形中,互相平行的一组对边叫做梯形的上底和下底;
故选A.
11. 3 7 3
【详解】略
12. 无数 1
【分析】平行四边形具有易变形性。用这四根小棒搭出一个平行四边形后,拽住一个角拉伸,可以得到无数个平行四边形,这些平行四边形的四条边相同,但内角不同。三角形具有稳定性。用这三根小棒搭出一个三角形后,这个三角形很稳定,不能在拉伸过程中得到其余的三角形,也就是只能搭出一个三角形。
【详解】用3厘米、3厘米、5厘米、5厘米的四根小棒,能搭出无数种平行四边形;用3厘米、4厘米、5厘米的三根小棒,能搭出1种三角形。
【点睛】本题关键是明确平行四边形具有易变形性,三角形具有稳定性。
13.垂直,平行
【详解】试题分析:由图可知:四边形DENM是长方形,则四个角都是直角,并且两组对边分别平行且相等;据此解答即可.
解:由分析可知:∠EDM=90°,即线段DE和线段DM互相垂直;
因为四边形DENM是长方形,即DE∥MN,则DE∥BC,
所以线段DE和线段BC互相平行;
故答案为垂直,平行.
点评:解答此题的关键:认真看图,根据长方形的特征及性质进行解答.
14.直,互相垂直,垂线,垂足
【详解】试题分析:根据垂直的含义:在同一平面内相交成直角的两条直线叫做互相垂直,其中一条直线叫作另一条直线的垂线;据此解答.
解:如图所示,直线a和直线b相交成直角,a和b互相垂直,a是b的垂线,交点O叫做垂足;
故答案为直,互相垂直,垂线,垂足.
点评:明确垂直的含义,是解答此题的关键.
15.(1)两把三角尺相交放置,如果两把三角尺各有一条边紧贴面,且另一条直角边都能紧贴另一平面,则平面与平面垂直.
(2)如果铅垂线与待测的平面紧贴,那么待测的平面与水平面垂直;
【详解】试题分析:只要两个平面中的一个直线与另下平面与它相交的直线垂直,那么这两个平面就相互垂直.据此解答.
解:根据分析知:
(1)两把三角尺相交放置,如果两把三角尺各有一条边紧贴面,且另一条直角边都能紧贴另一平面,则平面与平面垂直.
(2)如果铅垂线与待测的平面紧贴,那么待测的平面与水平面垂直;
点评:本题的关键是检验两个平面内相交的两条直线是否垂直.
16.错误
【分析】平行四边形有两组对边分别平行,做高时要弄清楚底和高应该相对应.
【详解】这种画高的方法是错误的,正确的如下图所示:
根据平行四边形高的概念:从平行四边形一条边上的一点到对边引一条垂线,这点和垂足之间的线段叫平行四边形的高,那么平行四边形的底和高是相对应的,所以原题的画法是错误的.
故答案为错误.
17.×
【分析】平行四边形和长方形的周长就是围成它们的所有的线段的和,将长方形框架拉成一个平行四边形后,每条线段长度没有变化,所以周长不变;据此判断即可。
【详解】因为把一个长方形拉成一个平行四边形后,四条边的长度没变,则四条边的长度和不变,即它的周长不变;所以原题的说法错误。
故答案为:×
【点睛】解答此题的关键是明确四边形的形状虽然发生了变化,但四条边的长度没有变化,周长就不发生变化。
18.×
【分析】根据平行四边形活动框架拉成长方形后各条边的变化来进行判断.
【详解】平行四边形活动框架拉成长方形之后,每条边的长度不变,所以周长不变.
19.×
【分析】要正确辨识长方形和平行四边形。
【详解】长方形是特殊的平行四边形。
【点睛】考查了长方形和平行四边形的定义。
20.√
【详解】只有一组对边互相平行的四边形叫梯形,在梯形里,互相平行的一组对边分别叫做梯形的上底和下底,此题说法正确.
故答案为正确.
21.14米;40米;48米
【分析】(1)平行四边形的周长等于相邻两条边的长度和的2倍,则平行四边形的周长是(4+3)×2米。
(2)
将图形的边平移后,可知图形的周长等于边长为10米的正方形的周长,根据正方形的周长=边长×4解答。
(3)
将图形的边平移后,可知图形的周长等于长15米宽9米的长方形的周长,根据长方形的周长=(长+宽)×2解答。
【详解】(1)(4+3)×2
=7×2
=14(米)
平行四边形的周长是14米。
(2)10×4=40(米)
图形的周长是40米。
(3)(15+9)×2
=24×2
=48(米)
图形的周长是48米。
22.(1)如图(1)通过测量可知三角形三条边的长度都是5cm,所以这个三角形是等边三角形.
(2)如图(2).
(3)如图(3),因为AD∥BC,AB∥CD,所以图形ABCD是平行四边形.
故答案为:等边;平行四边.
【详解】试题分析:(1)量三个角的度数或每条边的长度,根据三角形的分类可作出判断.
(2)根据高的做法画图即可解答.
(3)根据要求先画图,再根据平行四边形的性质可作出判断.
解:(1)如图(1)通过测量可知三角形三条边的长度都是5cm,所以这个三角形是等边三角形.
(2)如图(2).
(3)如图(3),因为AD∥BC,AB∥CD,所以图形ABCD是平行四边形.
故答案为等边;平行四边.
点评:本题主要考查等边三角形与平行四边形的定义,三条边或三个内角都相等的三角形为等边三角形,两组对边分别平行的四边形为平行四边形.
23.
【详解】试题分析:(1)用三角板的一条直角边的已知直线AC重合,沿重合的直线AC平移三角板,使三角板的另一条直角边和O点重合,过O沿直角边向已知AC直线画直线即可.
(2)把三角板的一条直角边与已知直线AB重合,用直尺靠紧三角板的另一条直角边,沿直尺移动三角板,使三角板的原来和已知直线AB重合的直角边和O点重合,过O点沿三角板的直角边画直线即可.据此解答.
解:根据分析画图如下:
点评:本题主要考查了学生画垂线和平行线的能力.
24.
【详解】试题分析:在平行四边形中,从一条边上的任意一点向对边作垂线,这点与垂足间的距离叫做以这条边为底的平行四边形的高,平行四边形有无数条高,习惯上作平行四边形的高时都从一个顶点出发作一边的垂线,用三角板的直角可以画出平行四形的高;梯形两底间的距离叫做梯形的高,梯形也有无数条高,通常过上底的一个顶点作下底的垂线用三角板的直角可以画出梯形的一条高.
解:作平行四边形、梯形的高如下:
故答案为
点评:本题是考查作平行四边形、梯形的高.注意作高用虚线,并标出垂足.
25.
【详解】试题分析:如图,根据平行四边形的特征,对边平行且相等,连接点A和线段的一个端点B,过线段的另一个端点C作CD∥AB,且CD=AB,连接AD就是用点A和线段L画一个平行四边形,或连接AB,过点A作AD∥BC,且AD=BC,连接CD就是用点A和线段L画一个平行四边形;经过平行四边形底上的一个顶点用三角板的直角边向另一底作垂线,顶点和垂足之间的线段就是平行四边形的一条高,平行四边形有无数条高,习惯上作平行四边形的高时,都从一个顶点出发向底作垂线.
解:由分析作图如下:
点评:本题主要是考查画平行四边形及作平行四边形的高.画平行四边形时,要根据平行四边形的特征画.
26.错误
【详解】试题分析:根据平行线的定义:在同一平面内,不相交的两条直线叫平行线,即可判断.
解:因为本题说的不是直线,所以说是平行线,说法错误;
故答案为×.
点评:此题主要考查了平行线的定义,关键是注意两点:①在同一平面内②不相交的两条直线.
同课章节目录
