数学:1.2《独立性检测的基本思想及其初步应用》课件(新人教a版选修1-2)
文档属性
| 名称 | 数学:1.2《独立性检测的基本思想及其初步应用》课件(新人教a版选修1-2) |

|
|
| 格式 | rar | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2010-01-27 00:00:00 | ||
图片预览







文档简介
课件28张PPT。新课标人教版课件系列《高中数学》
选修1-21.2《独立性检验的 基本思想及其初步应用》审校:王伟教学目标 1理解独立性检验的基本思想
2、会从列联表、柱形图、条形图直观判断吸烟与患癌有关。
3、了解随机变量K2的含义。
理解独立性检验的基本思想及实施步骤。
教学重点:理解独立性检验的基本思想。独立性检验的步骤。
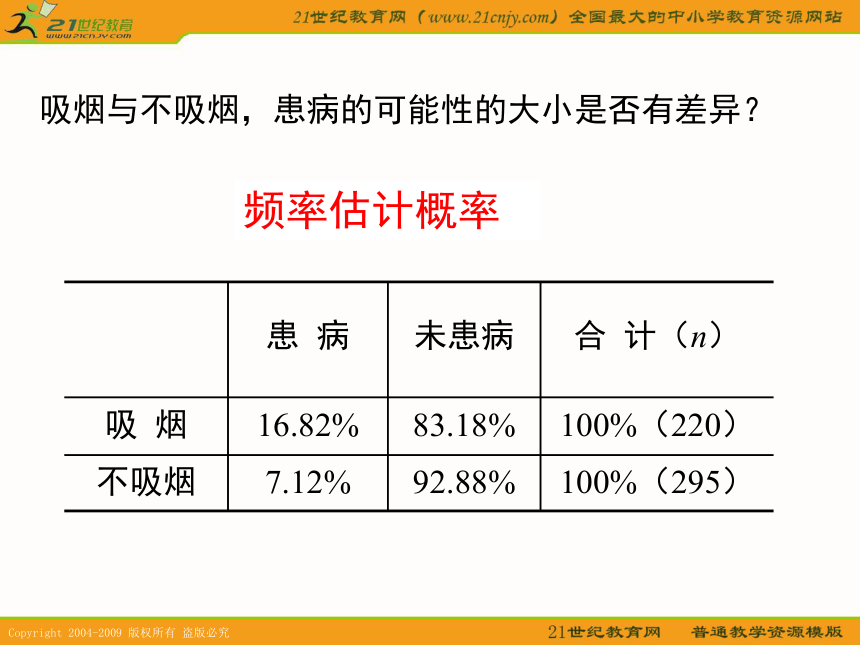
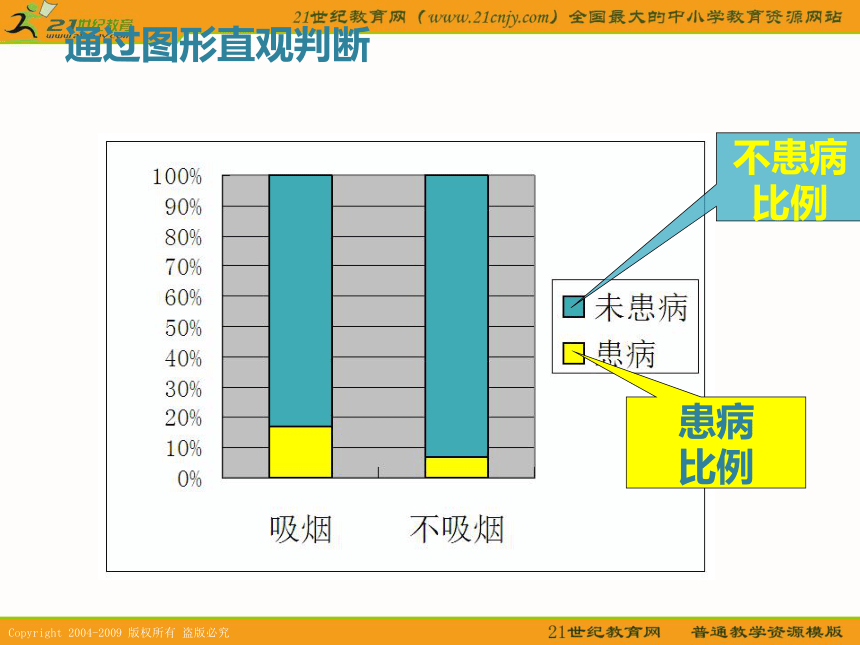
教学难点;1、理解独立性检验的基本思想;2、了解随机变量K2的含义;独立性检验的步骤。 看到这个课题,你能想到什么?案 例:某医疗机构为了了解呼吸道疾病与吸烟是否有关,进行了一次抽样调查,共调查了515个成年人,其中吸烟者220人,不吸烟者295人。调查结果:吸烟的220人中有37人患呼吸道疾病,183人未患呼吸道疾病;不吸烟的295人中有21人患病,274人未患病。根据这些数据,能否断定:患呼吸道疾病与吸烟有关?数据整理372158183274457220295515问题:判断的标准是什么?吸烟与不吸烟,患病的可能性的大小是否有差异?频率估计概率通过图形直观判断不患病
比例患病
比例解决问题:直观方法你能有多大把握认为“患病与吸烟有关”呢? 有一个颠扑不破的真理,那就是当我们不能确定什么是真的时,我们就应该去探求什么是最可能的。笛卡尔能否用数量来刻画“有关”程度问题的数学表述“患呼吸道疾病与吸烟有关”这句话是什么意思?
“某成年人吸烟”记为事件A, “某成年人患病”记为事件B
这句话的意思是:事件A与事件B有关。
问题的另一面是:事件A与事件B独立。
372158183274457220295515一般化:P(A)、P(B)不知道,怎么办?频率估计概率P(A) ? P(B) ? P(AB) ? ?同理,吸烟但不患病的人数约为n ? ?由此估计:
吸烟且患病的人数约为
n ? ?不吸烟但患病的人数约为n ? ?不吸烟也不患病的人数约为n ? ?怎样估计实际观测值与理论估计值的误差?采用如下的量(称为χ2 统计量)来刻画这个差异:+++化简得?2统计量?2 =11.8634解决问题的思路思路:反证法思想
(1)假设:H0:患病与吸烟无关
即 P(A)P(B)= P(AB)
(2)在 H0成立的条件下进行推理
(3)如果实际观测值与由(2)推出的值相差不大,则可以认为这些差异是由随机误差造成的,假设H0不能被否定;否则,假设H0不能被接受反证法原理与假设检验原理反证法原理: 在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。假设检验原理:在一个已知假设下,如果推出一个小概率事件发生,则推断这个假设不成立的可能性很大。一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类
取值,即类A和B(如吸烟与不吸烟);Ⅱ也有两类
取值,即类1和2(如患病与不患病)。于是得到
下列联表所示的抽样数据:要推断“Ⅰ和Ⅱ有关系”,可按下面的步骤进行:(1)提出假设H0 :Ⅰ和Ⅱ没有关系;(3)查对临界值,作出判断。(2)根据2× 2列联表与公式计算 的值; 由于抽样的随机性,由样本得到的推断有可能正确,也有可能错误。利用 进行独立性检验,可以对推断的正确性的概率作出估计,样本量n越大,估计越准确。卡方临界值表:则有99.9%的把握认为“Ⅰ与Ⅱ有关系”;(1)若观测值χ2>10.828.(3)若观测值χ2>2.706,则(4)若观测值χ2<2.706,则(2)若观测值χ2>6.635,则有99%的把握认为“Ⅰ与Ⅱ有关系”;则有90%的把握认为“Ⅰ与Ⅱ有关系”;则没有充分的证据显示“Ⅰ与Ⅱ有关系”,但也不能作出结论“H0成立”,即Ⅰ与Ⅱ没有关系。例2:为研究不同的给药方式(口服与注射)和药的效果(有效和无效)是否有关,进行了相应的抽样调查,调查的结果列在下表中,根据所选择的193个病人的数据,能否作出药的效果与给药方式有关的结论?解:提出假设
H0:药的效果与给药方式无关系。
根据列联表中的数据可以求出:当H0成立时, 的概率大于10%,这个概率比较大,所以根据目前的调查数据,不能否定假设H0,即不能作出药的效果与给药方式有关的结论。小结:1、所学的知识;2、解决问题的思路;3、假设检验原理。再见
选修1-21.2《独立性检验的 基本思想及其初步应用》审校:王伟教学目标 1理解独立性检验的基本思想
2、会从列联表、柱形图、条形图直观判断吸烟与患癌有关。
3、了解随机变量K2的含义。
理解独立性检验的基本思想及实施步骤。
教学重点:理解独立性检验的基本思想。独立性检验的步骤。
教学难点;1、理解独立性检验的基本思想;2、了解随机变量K2的含义;独立性检验的步骤。 看到这个课题,你能想到什么?案 例:某医疗机构为了了解呼吸道疾病与吸烟是否有关,进行了一次抽样调查,共调查了515个成年人,其中吸烟者220人,不吸烟者295人。调查结果:吸烟的220人中有37人患呼吸道疾病,183人未患呼吸道疾病;不吸烟的295人中有21人患病,274人未患病。根据这些数据,能否断定:患呼吸道疾病与吸烟有关?数据整理372158183274457220295515问题:判断的标准是什么?吸烟与不吸烟,患病的可能性的大小是否有差异?频率估计概率通过图形直观判断不患病
比例患病
比例解决问题:直观方法你能有多大把握认为“患病与吸烟有关”呢? 有一个颠扑不破的真理,那就是当我们不能确定什么是真的时,我们就应该去探求什么是最可能的。笛卡尔能否用数量来刻画“有关”程度问题的数学表述“患呼吸道疾病与吸烟有关”这句话是什么意思?
“某成年人吸烟”记为事件A, “某成年人患病”记为事件B
这句话的意思是:事件A与事件B有关。
问题的另一面是:事件A与事件B独立。
372158183274457220295515一般化:P(A)、P(B)不知道,怎么办?频率估计概率P(A) ? P(B) ? P(AB) ? ?同理,吸烟但不患病的人数约为n ? ?由此估计:
吸烟且患病的人数约为
n ? ?不吸烟但患病的人数约为n ? ?不吸烟也不患病的人数约为n ? ?怎样估计实际观测值与理论估计值的误差?采用如下的量(称为χ2 统计量)来刻画这个差异:+++化简得?2统计量?2 =11.8634解决问题的思路思路:反证法思想
(1)假设:H0:患病与吸烟无关
即 P(A)P(B)= P(AB)
(2)在 H0成立的条件下进行推理
(3)如果实际观测值与由(2)推出的值相差不大,则可以认为这些差异是由随机误差造成的,假设H0不能被否定;否则,假设H0不能被接受反证法原理与假设检验原理反证法原理: 在一个已知假设下,如果推出一个矛盾,就证明了这个假设不成立。假设检验原理:在一个已知假设下,如果推出一个小概率事件发生,则推断这个假设不成立的可能性很大。一般地,对于两个研究对象Ⅰ和Ⅱ,Ⅰ有两类
取值,即类A和B(如吸烟与不吸烟);Ⅱ也有两类
取值,即类1和2(如患病与不患病)。于是得到
下列联表所示的抽样数据:要推断“Ⅰ和Ⅱ有关系”,可按下面的步骤进行:(1)提出假设H0 :Ⅰ和Ⅱ没有关系;(3)查对临界值,作出判断。(2)根据2× 2列联表与公式计算 的值; 由于抽样的随机性,由样本得到的推断有可能正确,也有可能错误。利用 进行独立性检验,可以对推断的正确性的概率作出估计,样本量n越大,估计越准确。卡方临界值表:则有99.9%的把握认为“Ⅰ与Ⅱ有关系”;(1)若观测值χ2>10.828.(3)若观测值χ2>2.706,则(4)若观测值χ2<2.706,则(2)若观测值χ2>6.635,则有99%的把握认为“Ⅰ与Ⅱ有关系”;则有90%的把握认为“Ⅰ与Ⅱ有关系”;则没有充分的证据显示“Ⅰ与Ⅱ有关系”,但也不能作出结论“H0成立”,即Ⅰ与Ⅱ没有关系。例2:为研究不同的给药方式(口服与注射)和药的效果(有效和无效)是否有关,进行了相应的抽样调查,调查的结果列在下表中,根据所选择的193个病人的数据,能否作出药的效果与给药方式有关的结论?解:提出假设
H0:药的效果与给药方式无关系。
根据列联表中的数据可以求出:当H0成立时, 的概率大于10%,这个概率比较大,所以根据目前的调查数据,不能否定假设H0,即不能作出药的效果与给药方式有关的结论。小结:1、所学的知识;2、解决问题的思路;3、假设检验原理。再见
