2025年浙江省中考数学强基计划优质模拟卷(二十八)
文档属性
| 名称 | 2025年浙江省中考数学强基计划优质模拟卷(二十八) |  | |
| 格式 | docx | ||
| 文件大小 | 132.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 12:44:53 | ||
图片预览


文档简介
2025年浙江省中考数学强基计划优质模拟卷(二十八)
姓名 班级 学号
考生须知:
1.整卷共4页,有3个大题,共11个题,满分75分;考试时间为45分钟.
2.答题必须使用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
3.请将姓名、就读初中、中考报名序号填写在规定位置上.
一、选择题(每小题5分,共25分)
1.已知x=m是方程 的根,则代数式 的值是 ( )
A.1 B.2
2.如图,一次函数. 与二次函数 的图象相交于P,Q两点,则函数 2)x+c的图象可能是 ( )
3.如图,是正方形网格,除A,B两点外,在网格的格点上任取一点C,连结AC,BC,能使 为等腰三角形的概率是 ( )
4.如图, ,点E,F 分别是AC,BD的中点,I 则 的值等于
( )
B.24 C.30 D.36
5.直线y=kx+4与y轴相交于点A,与双曲线 相交于点B,C,且 则k的值是 ( )
或1 C.1
二、填空题(每小题5分,共20分)
6.关于x的不等式( )的解集是x<5,那么关于x的不等式 ax--b>0的解集是
7.已知y关于x的函数. (a为常量)的图象与坐标轴有且只有2个公共点,那么a 的值是 .
8.如图,A,B 两点在直线MN外的同侧,点A 到MN 的距离AC=8,点B到MN 的距离BD=5,CD=4,点 P 在直线MN上运动,则|PA-PB|的最大值等于 .
9.如图,已知三点A(-3,0)、B(0,4)、C(4,0),点D 在线段AC上,AD=AB,点P 在x轴上,点Q 在BC上,线段 PQ被BD 垂直平分,则点 P 的坐标是 .
中小学教育资源及组卷应用平台
三、解答题(共30分)
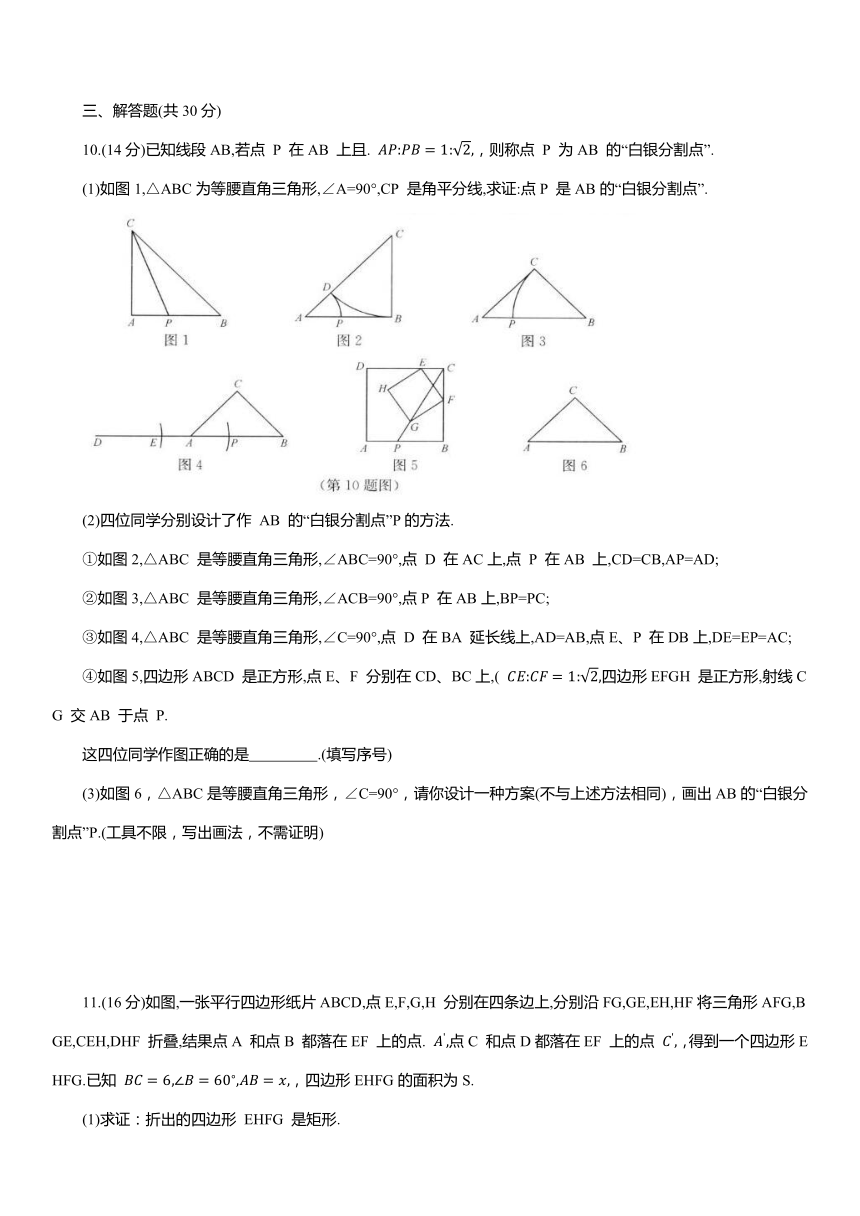
10.(14分)已知线段AB,若点 P 在AB 上且. ,则称点 P 为AB 的“白银分割点”.
(1)如图1,△ABC为等腰直角三角形,∠A=90°,CP 是角平分线,求证:点P 是AB的“白银分割点”.
(2)四位同学分别设计了作 AB 的“白银分割点”P的方法.
①如图2,△ABC 是等腰直角三角形,∠ABC=90°,点 D 在AC上,点 P 在AB 上,CD=CB,AP=AD;
②如图3,△ABC 是等腰直角三角形,∠ACB=90°,点P 在AB上,BP=PC;
③如图4,△ABC 是等腰直角三角形,∠C=90°,点 D 在BA 延长线上,AD=AB,点E、P 在DB上,DE=EP=AC;
④如图5,四边形ABCD 是正方形,点E、F 分别在CD、BC上,( 四边形EFGH 是正方形,射线CG 交AB 于点 P.
这四位同学作图正确的是 .(填写序号)
(3)如图6,△ABC是等腰直角三角形,∠C=90°,请你设计一种方案(不与上述方法相同),画出AB的“白银分割点”P.(工具不限,写出画法,不需证明)
11.(16分)如图,一张平行四边形纸片ABCD,点E,F,G,H 分别在四条边上,分别沿FG,GE,EH,HF将三角形AFG,BGE,CEH,DHF 折叠,结果点A 和点B 都落在EF 上的点. 点C 和点D都落在EF 上的点 ,得到一个四边形EHFG.已知 ,四边形EHFG的面积为S.
(1)求证:折出的四边形 EHFG 是矩形.
(2)求S 关于x的函数表达式.
(3)当x为多少时,四边形EHFG 是正方形
(4)当 时,求AF 的长(直接写出结果).
模拟卷(二十八)
1. A 2. A 3. D 4. D 5. B
7.1、0、- 8.5 9.( ,0)
10.解:(1)过点 P 作PD⊥BC 于点D,则△DPB 为等腰直角三角形,且 PD=PA,由 PD: PB=1: 得AP : PB=1: .所以点 P 为AB 的“白银分割点”.
(2)正确的有①③④.
(3)如图,作角平分线AD,作DP∥AC交AB 于点 P,那么点 P 即为所求的点.
11.(1)证明:由折纸可知∠AFG=∠EFG,∠EFH=∠DFH,
∴∠GFH=90°,
同理∠FGE=∠GEH=90°,
∴四边形EHFG 是矩形.
(2)解:如图1,连结GH,过点 A,F 作GH 的垂线,垂足分别为点 M,N.
又∵点 H 是CD的中点,
∴四边形 BCHG 是平行四边形,
∴GH=BC=6,
(3)解:当四边形EHFG是正方形时,S=6×6÷2=18,故 解得
(4)解: 或
解析:如图2,作矩形EHFG的外接圆O,在直线AD 上取一点Q,使OQ=OF=OH=3,过点O作OK⊥AD 于点K,连结EQ 交GH 于点 P,于是点Q在⊙O上.
由勾股定理,得 =OP,
而GM=1.65,
故 Q 在A,K 之间,
注:因∠GQH=90°,故 Q 点也可以作为矩形的顶点(如图3).
姓名 班级 学号
考生须知:
1.整卷共4页,有3个大题,共11个题,满分75分;考试时间为45分钟.
2.答题必须使用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
3.请将姓名、就读初中、中考报名序号填写在规定位置上.
一、选择题(每小题5分,共25分)
1.已知x=m是方程 的根,则代数式 的值是 ( )
A.1 B.2
2.如图,一次函数. 与二次函数 的图象相交于P,Q两点,则函数 2)x+c的图象可能是 ( )
3.如图,是正方形网格,除A,B两点外,在网格的格点上任取一点C,连结AC,BC,能使 为等腰三角形的概率是 ( )
4.如图, ,点E,F 分别是AC,BD的中点,I 则 的值等于
( )
B.24 C.30 D.36
5.直线y=kx+4与y轴相交于点A,与双曲线 相交于点B,C,且 则k的值是 ( )
或1 C.1
二、填空题(每小题5分,共20分)
6.关于x的不等式( )的解集是x<5,那么关于x的不等式 ax--b>0的解集是
7.已知y关于x的函数. (a为常量)的图象与坐标轴有且只有2个公共点,那么a 的值是 .
8.如图,A,B 两点在直线MN外的同侧,点A 到MN 的距离AC=8,点B到MN 的距离BD=5,CD=4,点 P 在直线MN上运动,则|PA-PB|的最大值等于 .
9.如图,已知三点A(-3,0)、B(0,4)、C(4,0),点D 在线段AC上,AD=AB,点P 在x轴上,点Q 在BC上,线段 PQ被BD 垂直平分,则点 P 的坐标是 .
中小学教育资源及组卷应用平台
三、解答题(共30分)
10.(14分)已知线段AB,若点 P 在AB 上且. ,则称点 P 为AB 的“白银分割点”.
(1)如图1,△ABC为等腰直角三角形,∠A=90°,CP 是角平分线,求证:点P 是AB的“白银分割点”.
(2)四位同学分别设计了作 AB 的“白银分割点”P的方法.
①如图2,△ABC 是等腰直角三角形,∠ABC=90°,点 D 在AC上,点 P 在AB 上,CD=CB,AP=AD;
②如图3,△ABC 是等腰直角三角形,∠ACB=90°,点P 在AB上,BP=PC;
③如图4,△ABC 是等腰直角三角形,∠C=90°,点 D 在BA 延长线上,AD=AB,点E、P 在DB上,DE=EP=AC;
④如图5,四边形ABCD 是正方形,点E、F 分别在CD、BC上,( 四边形EFGH 是正方形,射线CG 交AB 于点 P.
这四位同学作图正确的是 .(填写序号)
(3)如图6,△ABC是等腰直角三角形,∠C=90°,请你设计一种方案(不与上述方法相同),画出AB的“白银分割点”P.(工具不限,写出画法,不需证明)
11.(16分)如图,一张平行四边形纸片ABCD,点E,F,G,H 分别在四条边上,分别沿FG,GE,EH,HF将三角形AFG,BGE,CEH,DHF 折叠,结果点A 和点B 都落在EF 上的点. 点C 和点D都落在EF 上的点 ,得到一个四边形EHFG.已知 ,四边形EHFG的面积为S.
(1)求证:折出的四边形 EHFG 是矩形.
(2)求S 关于x的函数表达式.
(3)当x为多少时,四边形EHFG 是正方形
(4)当 时,求AF 的长(直接写出结果).
模拟卷(二十八)
1. A 2. A 3. D 4. D 5. B
7.1、0、- 8.5 9.( ,0)
10.解:(1)过点 P 作PD⊥BC 于点D,则△DPB 为等腰直角三角形,且 PD=PA,由 PD: PB=1: 得AP : PB=1: .所以点 P 为AB 的“白银分割点”.
(2)正确的有①③④.
(3)如图,作角平分线AD,作DP∥AC交AB 于点 P,那么点 P 即为所求的点.
11.(1)证明:由折纸可知∠AFG=∠EFG,∠EFH=∠DFH,
∴∠GFH=90°,
同理∠FGE=∠GEH=90°,
∴四边形EHFG 是矩形.
(2)解:如图1,连结GH,过点 A,F 作GH 的垂线,垂足分别为点 M,N.
又∵点 H 是CD的中点,
∴四边形 BCHG 是平行四边形,
∴GH=BC=6,
(3)解:当四边形EHFG是正方形时,S=6×6÷2=18,故 解得
(4)解: 或
解析:如图2,作矩形EHFG的外接圆O,在直线AD 上取一点Q,使OQ=OF=OH=3,过点O作OK⊥AD 于点K,连结EQ 交GH 于点 P,于是点Q在⊙O上.
由勾股定理,得 =OP,
而GM=1.65,
故 Q 在A,K 之间,
注:因∠GQH=90°,故 Q 点也可以作为矩形的顶点(如图3).
同课章节目录
