2025年浙江省中考数学强基计划优质模拟卷(二十二)(含答案)
文档属性
| 名称 | 2025年浙江省中考数学强基计划优质模拟卷(二十二)(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 134.0KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 10:16:33 | ||
图片预览


文档简介
2025年浙江省中考数学强基计划优质模拟卷(二十二)
姓名 班级 学号
考生须知:
1.整卷共4页,有3个大题,共11个题,满分75分;考试时间为45分钟.
2.答题必须使用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
3.请将姓名、就读初中、中考报名序号填写在规定位置上.
一、选择题(每小题5分,共25分)
1.设a,b,c是不为零的实数,那么 的值有 ( )
A.3种 B.4种 C.5种 D.6种
2.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是 ( )
A. a>1 B. a≤2 C.13.已知x+y+z=0,且 则代数式( 的值为 ( )
A.3 B.14 C.16 D.36
4.若直角三角形的一条直角边长为12,另两条边长均为整数,则符合这样条件的直角三角形的个数为
( )
A.3 B.4
C.6 D.无数多
5.如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连结BE,反比例函数 的图象经过点 D.已知 则k 的值是 ( )
A.
D.5
二、填空题(每小题5分,共20分)
6.在平面直角坐标系内有两点A(1,1),B(2,3).若一次函数. 的图象与线段AB 有公共点,则k 的取值范围为 .
7.已知 则 的值为 .
8.在 中,边BC上的高为1,点D 为AC的中点,则BD 的最小值为 .
9.设 若 为完全平方数,则整数n的个数为 .
三、解答题(共30分)
10.(12分)如果方程 的两个根是 那么 请根据以上结论,解决下列问题:
(1)已知关于x的方程 求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数.
(2)已知a,b满足 求 的值.
(3)已知a,b,c满足 求正数c的最小值.
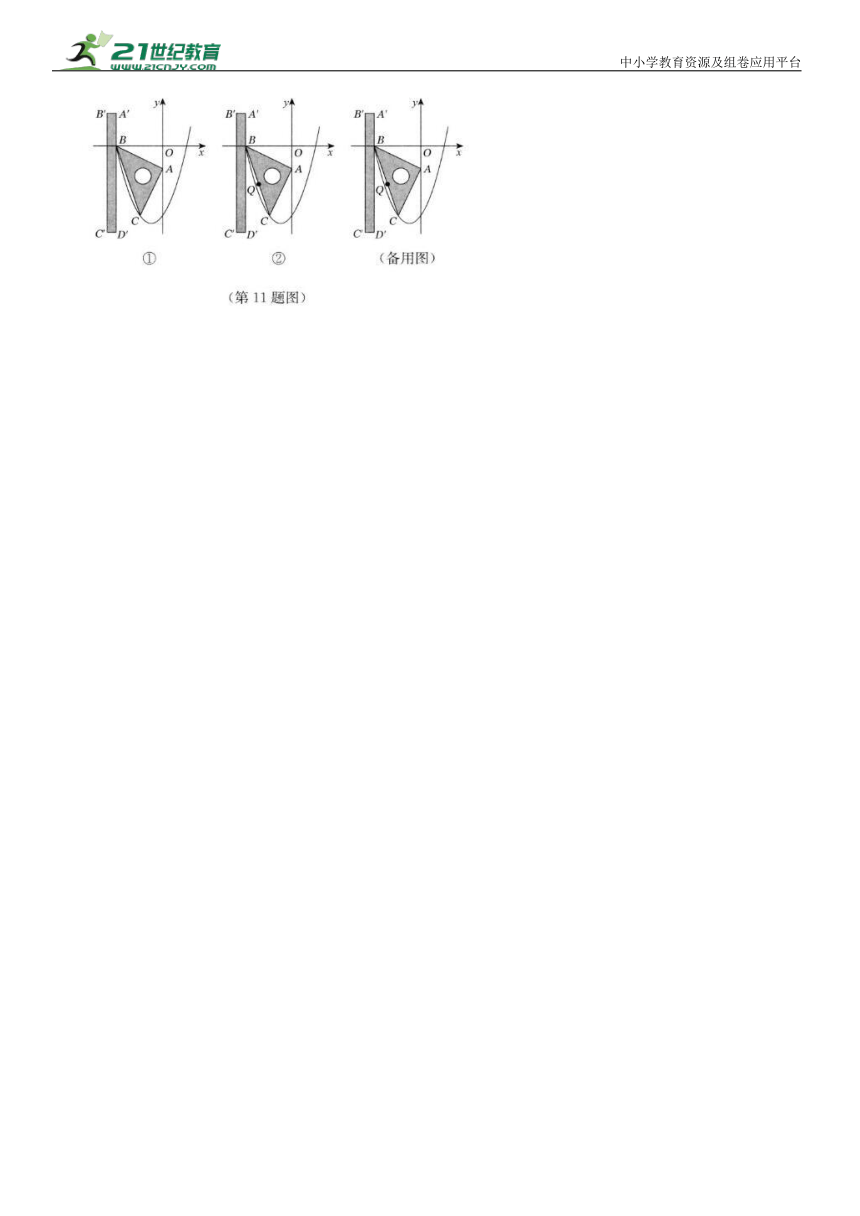
11.(18分)如图①,在平面直角坐标系中,一块等腰直角三角尺ABC的直角顶点A 在y轴上,坐标为 ,另一顶点 B 的坐标为( 已知二次函数 的图象经过B,C两点.现将一把直尺放置在直角坐标系中,使直尺的边 轴且经过点B,直尺沿x轴正方向平移,当 与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式.
(2)若运动过程中直尺的边 交边BC 于点M,交抛物线于点 N,求线段MN长度的最大值.
(3)如图②,设点 P 为直尺的边 上的任一点,连结PA,PB,PC,点Q为BC 的中点.试探究:在直尺平移的过程中,当 时,线段 PA,PB,PC之间的数量关系.请直接写出结论,并指出相应的点 P 与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A 在抛物线内,点C在抛物线上,点 在抛物线外)
中小学教育资源及组卷应用平台
模拟卷(二十二)
1. B 2. C 3. D 4. B 5. B
7.2 8 . 9 .13
10.解:(1)设方程x + mx+n=0(n≠0)的两个根分别是x ,x ,则
若一个一元二次方程的两个根分别是已知方程两根的倒数,
则这个一元二次方程是
(2)∵a,b满足 ∴a,b是 的解.
当a≠b时,a+b=15, ab=-5,
当a=b时,原式=2,
的值为-47或2.
(3)∵a+b+c=0, abc=16,
∴a,b是方程 的解,
即
∵c是正数,
∴c≥4,
∴正数c 的最小值是4.
11.解:(1)如答图1,过点 C 作CD⊥y轴于点 D,此时△CDA≌△AOB,
∴AD=BO=2,CD=AO=1,
∴OD=OA+AD=3,
∴C(--1,-3).
将B(-2,0),C(--1,--3)代入二次函数 ,得 解得 ∴二次函数的关系式为
(2)设lBC:y= kx+b.
∵B(-2,0),C(--1,-3),
解得
∴lBc:y=-3x-6.
设 ∵xm=xN(记为x),ym≥yn,
∴线段MN 的长度
∴当 时,线段 MN 的长度取得最大 值·
(3)点P 在抛物线外时,
点 P 在抛物线上时,
点 P 在抛物线内时,.
分析如下:
如答图2,以点 Q 为圆心 为半径作⊙Q.
∵OB=2,OA=1,
∴点B,A,C都在⊙Q 上.
①点 P 在抛物线外,
如答图3,⊙Q 与BD'的交点即为点P,连结PB,PC,PA,延长PC交y轴于点D.
∵BC 为⊙Q 的直径,
∴∠BPC=90°.
∵BD'与y轴平行,
∴∠ADC=90°,且点 D 为抛物线与 y 轴的交点,
∴PD∥x轴.
易得PC=1,PB=3,PA=2
②点 P 在抛物线上,此时,点P 只能为 B 点或C点.
③点 P 在抛物线内,有两种情况,如图4,5,如答图4,在PC上取BP=PT.
∵BC为⊙Q 的直径,
∴∠BPC=90°,
∴△BPT 为等腰直角三角形,
∵∠ABC=∠3+∠2=45°,
∴∠1=∠3.又∠BCT=∠BAP,
∴△BPA∽△BTC,
∵PC=PT+CT,
同理,如答图5,也可得
姓名 班级 学号
考生须知:
1.整卷共4页,有3个大题,共11个题,满分75分;考试时间为45分钟.
2.答题必须使用黑色字迹钢笔或签字笔书写,答案必须按照题号顺序在答题卷各题目规定区域内作答,做在试题卷上或超出答题区域书写的答案无效.
3.请将姓名、就读初中、中考报名序号填写在规定位置上.
一、选择题(每小题5分,共25分)
1.设a,b,c是不为零的实数,那么 的值有 ( )
A.3种 B.4种 C.5种 D.6种
2.已知x=2是不等式(x-5)(ax-3a+2)≤0的解,且x=1不是这个不等式的解,则实数a的取值范围是 ( )
A. a>1 B. a≤2 C.1
A.3 B.14 C.16 D.36
4.若直角三角形的一条直角边长为12,另两条边长均为整数,则符合这样条件的直角三角形的个数为
( )
A.3 B.4
C.6 D.无数多
5.如图,平行四边形ABCD的顶点C在y轴正半轴上,CD平行于x轴,直线AC交x轴于点E,BC⊥AC,连结BE,反比例函数 的图象经过点 D.已知 则k 的值是 ( )
A.
D.5
二、填空题(每小题5分,共20分)
6.在平面直角坐标系内有两点A(1,1),B(2,3).若一次函数. 的图象与线段AB 有公共点,则k 的取值范围为 .
7.已知 则 的值为 .
8.在 中,边BC上的高为1,点D 为AC的中点,则BD 的最小值为 .
9.设 若 为完全平方数,则整数n的个数为 .
三、解答题(共30分)
10.(12分)如果方程 的两个根是 那么 请根据以上结论,解决下列问题:
(1)已知关于x的方程 求出一个一元二次方程,使它的两个根分别是已知方程两根的倒数.
(2)已知a,b满足 求 的值.
(3)已知a,b,c满足 求正数c的最小值.
11.(18分)如图①,在平面直角坐标系中,一块等腰直角三角尺ABC的直角顶点A 在y轴上,坐标为 ,另一顶点 B 的坐标为( 已知二次函数 的图象经过B,C两点.现将一把直尺放置在直角坐标系中,使直尺的边 轴且经过点B,直尺沿x轴正方向平移,当 与y轴重合时运动停止.
(1)求点C的坐标及二次函数的关系式.
(2)若运动过程中直尺的边 交边BC 于点M,交抛物线于点 N,求线段MN长度的最大值.
(3)如图②,设点 P 为直尺的边 上的任一点,连结PA,PB,PC,点Q为BC 的中点.试探究:在直尺平移的过程中,当 时,线段 PA,PB,PC之间的数量关系.请直接写出结论,并指出相应的点 P 与抛物线的位置关系.
(说明:点与抛物线的位置关系可分为三类,例如,图②中,点A 在抛物线内,点C在抛物线上,点 在抛物线外)
中小学教育资源及组卷应用平台
模拟卷(二十二)
1. B 2. C 3. D 4. B 5. B
7.2 8 . 9 .13
10.解:(1)设方程x + mx+n=0(n≠0)的两个根分别是x ,x ,则
若一个一元二次方程的两个根分别是已知方程两根的倒数,
则这个一元二次方程是
(2)∵a,b满足 ∴a,b是 的解.
当a≠b时,a+b=15, ab=-5,
当a=b时,原式=2,
的值为-47或2.
(3)∵a+b+c=0, abc=16,
∴a,b是方程 的解,
即
∵c是正数,
∴c≥4,
∴正数c 的最小值是4.
11.解:(1)如答图1,过点 C 作CD⊥y轴于点 D,此时△CDA≌△AOB,
∴AD=BO=2,CD=AO=1,
∴OD=OA+AD=3,
∴C(--1,-3).
将B(-2,0),C(--1,--3)代入二次函数 ,得 解得 ∴二次函数的关系式为
(2)设lBC:y= kx+b.
∵B(-2,0),C(--1,-3),
解得
∴lBc:y=-3x-6.
设 ∵xm=xN(记为x),ym≥yn,
∴线段MN 的长度
∴当 时,线段 MN 的长度取得最大 值·
(3)点P 在抛物线外时,
点 P 在抛物线上时,
点 P 在抛物线内时,.
分析如下:
如答图2,以点 Q 为圆心 为半径作⊙Q.
∵OB=2,OA=1,
∴点B,A,C都在⊙Q 上.
①点 P 在抛物线外,
如答图3,⊙Q 与BD'的交点即为点P,连结PB,PC,PA,延长PC交y轴于点D.
∵BC 为⊙Q 的直径,
∴∠BPC=90°.
∵BD'与y轴平行,
∴∠ADC=90°,且点 D 为抛物线与 y 轴的交点,
∴PD∥x轴.
易得PC=1,PB=3,PA=2
②点 P 在抛物线上,此时,点P 只能为 B 点或C点.
③点 P 在抛物线内,有两种情况,如图4,5,如答图4,在PC上取BP=PT.
∵BC为⊙Q 的直径,
∴∠BPC=90°,
∴△BPT 为等腰直角三角形,
∵∠ABC=∠3+∠2=45°,
∴∠1=∠3.又∠BCT=∠BAP,
∴△BPA∽△BTC,
∵PC=PT+CT,
同理,如答图5,也可得
同课章节目录
