长沙市望城区第二中学2024-2025学年高二下学期6月第三次月考物理试卷(含答案)
文档属性
| 名称 | 长沙市望城区第二中学2024-2025学年高二下学期6月第三次月考物理试卷(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 664.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 物理 | ||
| 更新时间 | 2025-06-19 20:54:32 | ||
图片预览




文档简介
2025年上学期高二第三次月考
物理试题
一、单选题
1.如图所示为一列沿x轴正方向传播的简谐横波在某个时刻的波形图,由图像可知( )
A.质点b此时速度为零,势能为零
B.质点b此时向-y方向运动
C.质点d此时的振幅是0
D.质点a再经过通过的路程是4cm,偏离平衡位置的位移是-2cm
2.汽车在水平公路上运动时速度大小为108km/h,司机突然以5m/s2的加速度刹车,则刹车后 8s 内汽车滑行的距离为( )
A.50m B.70m C.90m D.110m
3.如图所示,某工地上起重机将重为G的正方形工件缓缓吊起,四根质量不计等长的钢绳,一端分别固定在正方形工件的四个角上,另一端汇聚于一处挂在挂钩上,每根绳与竖直方向的夹角为37°,则每根钢绳的受力大小为( )
A. B. C.G D.G
4.如图所示为电阻R1和R2的伏安特性曲线,并且把第一象限分为了Ⅰ、Ⅱ、Ⅲ三个区域.现把R1和R2并联在电路中,消耗的电功率分别用P1和P2表示;并联的总电阻设为R.下列关于P1与P2的大小关系及R的伏安特性曲线应该在的区域正确的是( )
A.特性曲线在Ⅰ区,P1<P2 B.特性曲线在Ⅲ区,P1<P2
C.特性曲线在Ⅰ区,P1>P2 D.特性曲线在Ⅲ区,P1>P2
5.如图所示为两个点电荷的电场,虚线为一带电粒子只在电场力作用下的运动轨迹,a、b为轨迹上两点,下列说法中正确的是( )
A.带电粒子带正电
B.带电粒子在a点的加速度大于在b点的加速度
C.带电粒子在a点的动能大于在b点的动能
D.左边点电荷所带电荷量多
6.如图甲,在水平地面上固定一倾角θ=37°、表面光滑的斜面体,物体A的质量为mA=0.1kg,以某一初速度沿斜面上滑,同时在物体A的正上方,一物体B的质量为mB=0.1kg,以某一初速度水平抛出。当A上滑到最高点C速度为0时恰好被物体B击中,规定相遇点所在平面为零势能面。A、B运动的高度h随动能Ek的变化关系图像如图乙所示,已知C点坐标为(1.8J,-1.8m)。A、B均可看成质点,不计空气阻力,sin37°=0.6,cos37°=0.8,g取10m/s2,则( )
A.物体B的初速度v0=2.4m/s
B.物体A从最低点运动到斜面最高点的时间t=1.2s
C.A、B起始时刻的高度差H=5m
D.B撞击A瞬间的动能Ek=5.4J
7.如图所示,在圆柱形区域内存在竖直向上的匀强磁场,磁感应强度的大小随时间的变化关系为,其中、为正的常数.在此区域的水平面内固定一个半径为的圆环形内壁光滑的细玻璃管,将一电荷量为的带正电小球在管内由静止释放,不考虑带电小球在运动过程中产生的磁场,则下列说法正确的是( )
A.从上往下看,小球将在管内沿顺时针方向运动,转动一周的过程中动能增量为
B.从上往下看,小球将在管内沿逆时针方向运动,转动一周的过程中动能增量为
C.从上往下看,小球将在管内沿顺时针方向运动,转动一周的过程中动能增量为
D.从上往下看,小球将在管内沿逆时针方向运动,转动一周的过程中动能增量为
二、多选题
8.我国核聚变反应研究大科学装置“人造太阳”2018年获得重大突破,等离子体中心电子温度首次达到1亿度,为人类开发利用核聚变能源奠定了重要的技术基础.下列关于聚变的说法正确的是( )
A.核聚变比核裂变更为安全、清洁
B.任何两个原子核都可以发生聚变
C.两个轻核结合成质量较大的核,总质量较聚变前增加
D.两个轻核结合成质量较大的核,核子的比结合能增加
9.如图所示,两个倾角分别为30°和60°的光滑绝缘斜面固定于水平地面上,并处于方向垂直纸面向里、磁感应强度为B的匀强磁场中,两个质量为m、带电荷量为+q的小滑块甲和乙分别从两个斜面顶端由静止释放,运动一段时间后,两小滑块都将飞离斜面,在此过程中( )
A.甲滑块飞离斜面瞬间的速度比乙滑块飞离斜面瞬间的速度大
B.甲滑块在斜面上运动的时间比乙滑块在斜面上运动的时间短
C.两滑块在斜面上运动的位移大小相同
D.两滑块在斜面上运动的过程中,重力的平均功率相等
10.一质量为m、可视为质点的物块B静止于质量为M的木板C左端,木板静止于光滑水平面上,将质量为m的小球A用长为L的细绳悬挂于O点,静止时小球A与B等高且刚好接触,现对小球A施加一外力,使细绳恰好水平,如图所示,现将外力撤去,小球A与物块B发生弹性碰撞,已知B、C间动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
A.小球A碰撞后做简谐运动
B.碰撞后物块B的速度为
C.若物块B未滑离木板C,则物块B与木板C之间的摩擦热为
D.若物块B会滑离木板C,则板长小于
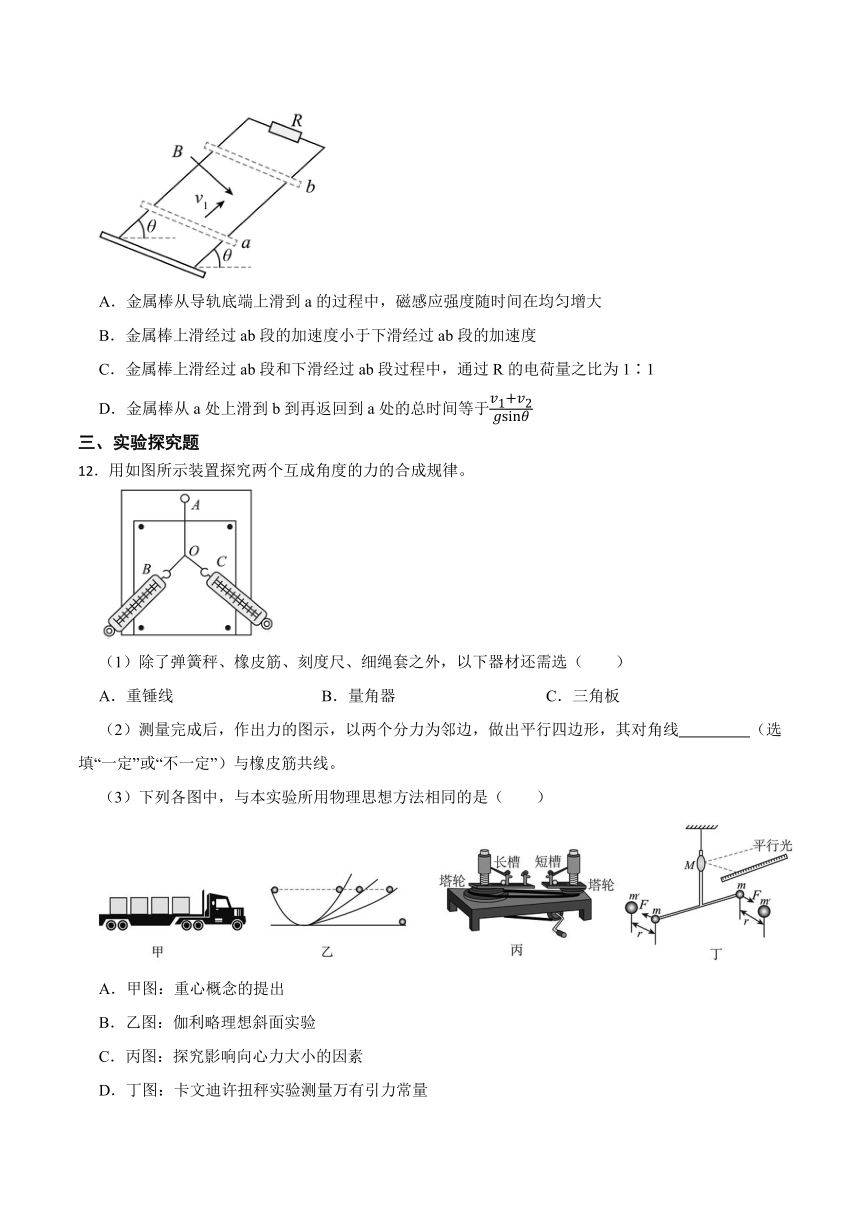
11.如图所示,足够长的光滑平行金属导轨与水平面成角放置,导轨电阻不计,其顶端接有一电阻,底端静止一金属棒。整个装置处于方向垂直于导轨平面向下的匀强磁场中,为了使金属棒沿导轨上滑,磁感应强度开始随时间均匀变化,当金属棒运动到a处时磁感应强度开始保持不变。金属棒运动刚到a处时的速度大小为,继续滑行一段距离到达最高点b后,再返回到a处时的速度大小为。重力加速度为g,则( )
A.金属棒从导轨底端上滑到a的过程中,磁感应强度随时间在均匀增大
B.金属棒上滑经过ab段的加速度小于下滑经过ab段的加速度
C.金属棒上滑经过ab段和下滑经过ab段过程中,通过R的电荷量之比为1∶1
D.金属棒从a处上滑到b到再返回到a处的总时间等于
三、实验探究题
12.用如图所示装置探究两个互成角度的力的合成规律。
(1)除了弹簧秤、橡皮筋、刻度尺、细绳套之外,以下器材还需选( )
A.重锤线 B.量角器 C.三角板
(2)测量完成后,作出力的图示,以两个分力为邻边,做出平行四边形,其对角线 (选填“一定”或“不一定”)与橡皮筋共线。
(3)下列各图中,与本实验所用物理思想方法相同的是( )
A.甲图:重心概念的提出
B.乙图:伽利略理想斜面实验
C.丙图:探究影响向心力大小的因素
D.丁图:卡文迪许扭秤实验测量万有引力常量
13.为测量干电池的电动势(约为)和内阻(约为),某同学将两节相同的干电池串联后设计了如图甲、乙所示的实验电路图。已知电流表的内阻约为,电压表的内阻约为,滑动变阻器最大电阻为。
(1)按照图甲所示的电路图,将图丙中的实物连线补充完整 。
(2)闭合开关S前,图丙中的滑动变阻器的滑片应移至最 (填“左”或“右”)端。
(3)闭合开关S后,移动滑片改变滑动变阻器接入的阻值,记录下多组电压表示数和对应的电流表示数,将实验记录的数据在坐标系内描点并作出图像。
(4)在图丙中通过改变导线的接线位置,完成了如图乙所示电路图的实物连接,重复步骤(2)(3)。将实验记录的数据在同一坐标系内描点并作出对应的图像,如图丁所示,图丁中、、、均已知。
(5)利用图丁中提供的信息可知,每节干电池的电动势的准确值为 ,每节干电池的内阻的准确值为 。
四、计算题
14.如图所示,一质量为0.1kg的小球,用40cm长的细绳拴住在竖直面内做圆周运动,()求:
(1)小球恰能通过圆周最高点时的速度多大?
(2)小球以3m/s的速度通过圆周最高点时,绳对小球的拉力多大?
(3)当小球在圆周最低点时,绳的拉力为10N,求此时小球的速度大小?
15.如图,间距为L的足够长平行光滑金属导轨上端固定在竖直立柱上,导轨与立柱的夹角为,导轨间接入一阻值为R的电阻D,水平虚线ab下方有磁感应强度大小为B的匀强磁场,方向垂直导轨平面向上。一质量为m的金属棒在水平推力作用下静止在图示位置,与虚线ab间的距离为,撤去推力后,金属棒沿导轨下滑,与导轨始终垂直且接触良好。接入导轨间的金属棒阻值也为R,不计导轨电阻,重力加速度大小为g。
(1)求金属棒静止时所受到的水平推力大小;
(2)求金属棒刚进入磁场时通过电阻D的电流大小;
(3)从撤去推力至金属棒速度达到最大的过程中,电阻D产生的热量为Q,求该过程金属棒下滑的总距离。
16.如图所示,导轨MN、PQ足够长,与水平面夹角为θ,两导轨上端接有电阻和电容器,R、C分别表示电阻的大小和电容的大小,P处连有一单刀双掷开关S,两导轨平行且相距为L,整个装置处在垂直于该平面向下的匀强磁场中,磁感应强度大小为B,质量为m、长为L的导体棒ab在外力作用下垂直静置于导轨上(导体棒电阻不计),ab与导轨间的动摩擦因数为,重力加速度为g,ab与导轨间接触始终良好。
(1)将单刀双掷开关S置于1,ab从静止释放(撤去外力),经时间t刚好达到最大速度,求这个过程中R产生的焦耳热;
(2)将单刀双掷开关S置于2,ab从静止释放(撤去外力),试判断ab的加速度是否恒定,请详细说明推理过程;
(3)将单刀双掷开关S置于2,ab从静止释放(撤去外力),ab沿导轨下滑距离为s时,求电容器所带电荷量。
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】C
8.【答案】A,D
9.【答案】A,D
10.【答案】B,C,D
11.【答案】A,C,D
12.【答案】(1)C
(2)不一定
(3)A
13.【答案】;右;;
14.【答案】(1)解:小球做圆周运动的半径,当细线拉力为零时,有
解得
(2)解:根据牛顿第二定律得
解得
(3)解:根据牛顿第二定律得
代入数据解得
【解析】【分析】(1)根据题意确定小球做圆周运动的半径,确定绳子拉力为零时,小球的受力情况及向心力的来源,再结合牛顿第二定律进行解答;
(2)由(1)可知,此时重力不足以提供向心力,小球同时受到绳子的拉力和重力作用,再结合牛顿第二定律进行解答;
(3)确定小球的受力情况及向心力的来源,再结合牛顿第二定律进行解答。
15.【答案】(1)解:金属棒静止时,合力为零,设受到的水平推力大小为F,则
可得
(2)解:设撤去水平推力后,金属棒进入磁场的速度大小为,由机械能守恒可得
则进入磁场时产生的电动势为
通过电阻R上的电流为
可得
(3)解:设金属棒运动的最大速度,下滑的总距离为x,则最大电流为
由能量守恒可得
可得
【解析】【分析】(1)静止时,金属棒处于平衡状态,对其进行受力分析,根据平衡条件及力的合成与分解进行求解;
(2)撤去推力后,分析金属棒的运动情况。当金属棒进入磁场时,金属棒切割磁场产生动生电动势。可根据功能关系或匀变速直线运动求解金属棒进入磁场时的速度。再根据电磁感应定律的推导式及闭合电路中的欧姆定律进行解答;
(3)金属棒进入磁场后,做加速度减小的加速运动,当速度最大时,金属棒的加速度为零,根据其受力情况列出此时的平衡方程。由于金属棒阻值与电阻D阻值相等,所以两者产生的焦耳热相等。再根据能量守恒定律进行求解。
16.【答案】(1)解:当S置于1,导体棒的速度达到最大时,合外力为零,对导体棒受力分析,如图所示,有
由闭合电路欧姆定律得,
由法拉第电磁感应定律得,
解得,
由动量定理得,
又,,
解得,
由能量守恒得R产生的热量为
(2)解:,取极短的时间有,,,
联立解得,
由牛顿第二定律得,
解得,为定值,故ab的加速度恒定。
(3)解:由(2)得
解得
又,,解得
【解析】【分析】(1)达到最大速度时导体棒受力平衡, 结合法拉第电磁感应定律求解最大速度,利用动量定理以及电荷量的求解得到下滑距离, 由能量守恒得R产生的热量 。
(2)取极短的时间得到电流表达式,得到安培力的表达式,由牛顿第二定律得加速度表达式;
(3)加速度恒定,为匀变速直线运动,求解ab沿导轨下滑距离为s时的速度,电荷量等于电压与电容的乘积。
物理试题
一、单选题
1.如图所示为一列沿x轴正方向传播的简谐横波在某个时刻的波形图,由图像可知( )
A.质点b此时速度为零,势能为零
B.质点b此时向-y方向运动
C.质点d此时的振幅是0
D.质点a再经过通过的路程是4cm,偏离平衡位置的位移是-2cm
2.汽车在水平公路上运动时速度大小为108km/h,司机突然以5m/s2的加速度刹车,则刹车后 8s 内汽车滑行的距离为( )
A.50m B.70m C.90m D.110m
3.如图所示,某工地上起重机将重为G的正方形工件缓缓吊起,四根质量不计等长的钢绳,一端分别固定在正方形工件的四个角上,另一端汇聚于一处挂在挂钩上,每根绳与竖直方向的夹角为37°,则每根钢绳的受力大小为( )
A. B. C.G D.G
4.如图所示为电阻R1和R2的伏安特性曲线,并且把第一象限分为了Ⅰ、Ⅱ、Ⅲ三个区域.现把R1和R2并联在电路中,消耗的电功率分别用P1和P2表示;并联的总电阻设为R.下列关于P1与P2的大小关系及R的伏安特性曲线应该在的区域正确的是( )
A.特性曲线在Ⅰ区,P1<P2 B.特性曲线在Ⅲ区,P1<P2
C.特性曲线在Ⅰ区,P1>P2 D.特性曲线在Ⅲ区,P1>P2
5.如图所示为两个点电荷的电场,虚线为一带电粒子只在电场力作用下的运动轨迹,a、b为轨迹上两点,下列说法中正确的是( )
A.带电粒子带正电
B.带电粒子在a点的加速度大于在b点的加速度
C.带电粒子在a点的动能大于在b点的动能
D.左边点电荷所带电荷量多
6.如图甲,在水平地面上固定一倾角θ=37°、表面光滑的斜面体,物体A的质量为mA=0.1kg,以某一初速度沿斜面上滑,同时在物体A的正上方,一物体B的质量为mB=0.1kg,以某一初速度水平抛出。当A上滑到最高点C速度为0时恰好被物体B击中,规定相遇点所在平面为零势能面。A、B运动的高度h随动能Ek的变化关系图像如图乙所示,已知C点坐标为(1.8J,-1.8m)。A、B均可看成质点,不计空气阻力,sin37°=0.6,cos37°=0.8,g取10m/s2,则( )
A.物体B的初速度v0=2.4m/s
B.物体A从最低点运动到斜面最高点的时间t=1.2s
C.A、B起始时刻的高度差H=5m
D.B撞击A瞬间的动能Ek=5.4J
7.如图所示,在圆柱形区域内存在竖直向上的匀强磁场,磁感应强度的大小随时间的变化关系为,其中、为正的常数.在此区域的水平面内固定一个半径为的圆环形内壁光滑的细玻璃管,将一电荷量为的带正电小球在管内由静止释放,不考虑带电小球在运动过程中产生的磁场,则下列说法正确的是( )
A.从上往下看,小球将在管内沿顺时针方向运动,转动一周的过程中动能增量为
B.从上往下看,小球将在管内沿逆时针方向运动,转动一周的过程中动能增量为
C.从上往下看,小球将在管内沿顺时针方向运动,转动一周的过程中动能增量为
D.从上往下看,小球将在管内沿逆时针方向运动,转动一周的过程中动能增量为
二、多选题
8.我国核聚变反应研究大科学装置“人造太阳”2018年获得重大突破,等离子体中心电子温度首次达到1亿度,为人类开发利用核聚变能源奠定了重要的技术基础.下列关于聚变的说法正确的是( )
A.核聚变比核裂变更为安全、清洁
B.任何两个原子核都可以发生聚变
C.两个轻核结合成质量较大的核,总质量较聚变前增加
D.两个轻核结合成质量较大的核,核子的比结合能增加
9.如图所示,两个倾角分别为30°和60°的光滑绝缘斜面固定于水平地面上,并处于方向垂直纸面向里、磁感应强度为B的匀强磁场中,两个质量为m、带电荷量为+q的小滑块甲和乙分别从两个斜面顶端由静止释放,运动一段时间后,两小滑块都将飞离斜面,在此过程中( )
A.甲滑块飞离斜面瞬间的速度比乙滑块飞离斜面瞬间的速度大
B.甲滑块在斜面上运动的时间比乙滑块在斜面上运动的时间短
C.两滑块在斜面上运动的位移大小相同
D.两滑块在斜面上运动的过程中,重力的平均功率相等
10.一质量为m、可视为质点的物块B静止于质量为M的木板C左端,木板静止于光滑水平面上,将质量为m的小球A用长为L的细绳悬挂于O点,静止时小球A与B等高且刚好接触,现对小球A施加一外力,使细绳恰好水平,如图所示,现将外力撤去,小球A与物块B发生弹性碰撞,已知B、C间动摩擦因数为μ,重力加速度为g,则下列说法正确的是( )
A.小球A碰撞后做简谐运动
B.碰撞后物块B的速度为
C.若物块B未滑离木板C,则物块B与木板C之间的摩擦热为
D.若物块B会滑离木板C,则板长小于
11.如图所示,足够长的光滑平行金属导轨与水平面成角放置,导轨电阻不计,其顶端接有一电阻,底端静止一金属棒。整个装置处于方向垂直于导轨平面向下的匀强磁场中,为了使金属棒沿导轨上滑,磁感应强度开始随时间均匀变化,当金属棒运动到a处时磁感应强度开始保持不变。金属棒运动刚到a处时的速度大小为,继续滑行一段距离到达最高点b后,再返回到a处时的速度大小为。重力加速度为g,则( )
A.金属棒从导轨底端上滑到a的过程中,磁感应强度随时间在均匀增大
B.金属棒上滑经过ab段的加速度小于下滑经过ab段的加速度
C.金属棒上滑经过ab段和下滑经过ab段过程中,通过R的电荷量之比为1∶1
D.金属棒从a处上滑到b到再返回到a处的总时间等于
三、实验探究题
12.用如图所示装置探究两个互成角度的力的合成规律。
(1)除了弹簧秤、橡皮筋、刻度尺、细绳套之外,以下器材还需选( )
A.重锤线 B.量角器 C.三角板
(2)测量完成后,作出力的图示,以两个分力为邻边,做出平行四边形,其对角线 (选填“一定”或“不一定”)与橡皮筋共线。
(3)下列各图中,与本实验所用物理思想方法相同的是( )
A.甲图:重心概念的提出
B.乙图:伽利略理想斜面实验
C.丙图:探究影响向心力大小的因素
D.丁图:卡文迪许扭秤实验测量万有引力常量
13.为测量干电池的电动势(约为)和内阻(约为),某同学将两节相同的干电池串联后设计了如图甲、乙所示的实验电路图。已知电流表的内阻约为,电压表的内阻约为,滑动变阻器最大电阻为。
(1)按照图甲所示的电路图,将图丙中的实物连线补充完整 。
(2)闭合开关S前,图丙中的滑动变阻器的滑片应移至最 (填“左”或“右”)端。
(3)闭合开关S后,移动滑片改变滑动变阻器接入的阻值,记录下多组电压表示数和对应的电流表示数,将实验记录的数据在坐标系内描点并作出图像。
(4)在图丙中通过改变导线的接线位置,完成了如图乙所示电路图的实物连接,重复步骤(2)(3)。将实验记录的数据在同一坐标系内描点并作出对应的图像,如图丁所示,图丁中、、、均已知。
(5)利用图丁中提供的信息可知,每节干电池的电动势的准确值为 ,每节干电池的内阻的准确值为 。
四、计算题
14.如图所示,一质量为0.1kg的小球,用40cm长的细绳拴住在竖直面内做圆周运动,()求:
(1)小球恰能通过圆周最高点时的速度多大?
(2)小球以3m/s的速度通过圆周最高点时,绳对小球的拉力多大?
(3)当小球在圆周最低点时,绳的拉力为10N,求此时小球的速度大小?
15.如图,间距为L的足够长平行光滑金属导轨上端固定在竖直立柱上,导轨与立柱的夹角为,导轨间接入一阻值为R的电阻D,水平虚线ab下方有磁感应强度大小为B的匀强磁场,方向垂直导轨平面向上。一质量为m的金属棒在水平推力作用下静止在图示位置,与虚线ab间的距离为,撤去推力后,金属棒沿导轨下滑,与导轨始终垂直且接触良好。接入导轨间的金属棒阻值也为R,不计导轨电阻,重力加速度大小为g。
(1)求金属棒静止时所受到的水平推力大小;
(2)求金属棒刚进入磁场时通过电阻D的电流大小;
(3)从撤去推力至金属棒速度达到最大的过程中,电阻D产生的热量为Q,求该过程金属棒下滑的总距离。
16.如图所示,导轨MN、PQ足够长,与水平面夹角为θ,两导轨上端接有电阻和电容器,R、C分别表示电阻的大小和电容的大小,P处连有一单刀双掷开关S,两导轨平行且相距为L,整个装置处在垂直于该平面向下的匀强磁场中,磁感应强度大小为B,质量为m、长为L的导体棒ab在外力作用下垂直静置于导轨上(导体棒电阻不计),ab与导轨间的动摩擦因数为,重力加速度为g,ab与导轨间接触始终良好。
(1)将单刀双掷开关S置于1,ab从静止释放(撤去外力),经时间t刚好达到最大速度,求这个过程中R产生的焦耳热;
(2)将单刀双掷开关S置于2,ab从静止释放(撤去外力),试判断ab的加速度是否恒定,请详细说明推理过程;
(3)将单刀双掷开关S置于2,ab从静止释放(撤去外力),ab沿导轨下滑距离为s时,求电容器所带电荷量。
答案解析部分
1.【答案】D
2.【答案】C
3.【答案】C
4.【答案】C
5.【答案】D
6.【答案】A
7.【答案】C
8.【答案】A,D
9.【答案】A,D
10.【答案】B,C,D
11.【答案】A,C,D
12.【答案】(1)C
(2)不一定
(3)A
13.【答案】;右;;
14.【答案】(1)解:小球做圆周运动的半径,当细线拉力为零时,有
解得
(2)解:根据牛顿第二定律得
解得
(3)解:根据牛顿第二定律得
代入数据解得
【解析】【分析】(1)根据题意确定小球做圆周运动的半径,确定绳子拉力为零时,小球的受力情况及向心力的来源,再结合牛顿第二定律进行解答;
(2)由(1)可知,此时重力不足以提供向心力,小球同时受到绳子的拉力和重力作用,再结合牛顿第二定律进行解答;
(3)确定小球的受力情况及向心力的来源,再结合牛顿第二定律进行解答。
15.【答案】(1)解:金属棒静止时,合力为零,设受到的水平推力大小为F,则
可得
(2)解:设撤去水平推力后,金属棒进入磁场的速度大小为,由机械能守恒可得
则进入磁场时产生的电动势为
通过电阻R上的电流为
可得
(3)解:设金属棒运动的最大速度,下滑的总距离为x,则最大电流为
由能量守恒可得
可得
【解析】【分析】(1)静止时,金属棒处于平衡状态,对其进行受力分析,根据平衡条件及力的合成与分解进行求解;
(2)撤去推力后,分析金属棒的运动情况。当金属棒进入磁场时,金属棒切割磁场产生动生电动势。可根据功能关系或匀变速直线运动求解金属棒进入磁场时的速度。再根据电磁感应定律的推导式及闭合电路中的欧姆定律进行解答;
(3)金属棒进入磁场后,做加速度减小的加速运动,当速度最大时,金属棒的加速度为零,根据其受力情况列出此时的平衡方程。由于金属棒阻值与电阻D阻值相等,所以两者产生的焦耳热相等。再根据能量守恒定律进行求解。
16.【答案】(1)解:当S置于1,导体棒的速度达到最大时,合外力为零,对导体棒受力分析,如图所示,有
由闭合电路欧姆定律得,
由法拉第电磁感应定律得,
解得,
由动量定理得,
又,,
解得,
由能量守恒得R产生的热量为
(2)解:,取极短的时间有,,,
联立解得,
由牛顿第二定律得,
解得,为定值,故ab的加速度恒定。
(3)解:由(2)得
解得
又,,解得
【解析】【分析】(1)达到最大速度时导体棒受力平衡, 结合法拉第电磁感应定律求解最大速度,利用动量定理以及电荷量的求解得到下滑距离, 由能量守恒得R产生的热量 。
(2)取极短的时间得到电流表达式,得到安培力的表达式,由牛顿第二定律得加速度表达式;
(3)加速度恒定,为匀变速直线运动,求解ab沿导轨下滑距离为s时的速度,电荷量等于电压与电容的乘积。
同课章节目录
