第一章 三角形的证明 检测卷 (含答案)2024-2025学年北师版数学八年级下册
文档属性
| 名称 | 第一章 三角形的证明 检测卷 (含答案)2024-2025学年北师版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 220.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:23:36 | ||
图片预览


文档简介
第一章 三角形的证明 检测卷
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
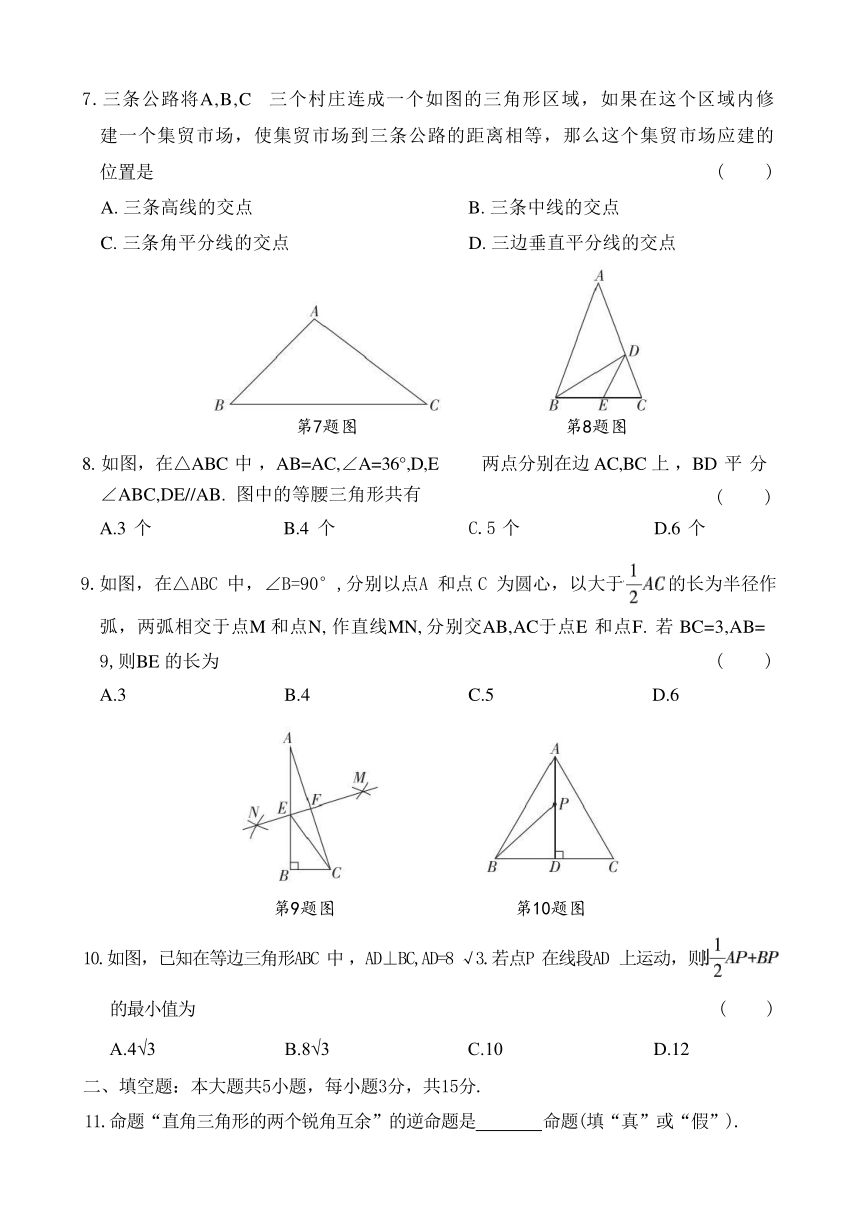
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.在等腰三角形ABC中 ,AB=AC,若∠A=70°, 则∠B 的度数是 ( ) A.40° B.55° C.65° D.60°
2.下列判定直角三角形全等的方法,错误的是 ( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一直角边对应相等 D. 两锐角相等
3.用反证法证明命题“在△ABC 中,若AB=AC, 则∠B<90°”时,第一步应该假设( )
A. ∠B>90° B. ∠B≥90°
C.AB≠AC D.AB≠AC 且∠B≥90°
4.如图,直线m//n,△ABC 是等边三角形,顶点B 在直线n 上,直线m 交 AB 于点E,交AC 于点F. 若∠1=140°,则∠2的度数是 ( ) A.110° B.105° C.100° D.95°
第4题图 第5题图 第6题图
5. 如图,在△ABC 中 ,AB=AC,AD 是△ABC的角平分线 .若 AB=13,AD=12, 则 BC 的长为 ( ) A.6 B.5 C.8 D.10
6.如图,在△ABC 中 ,CD 是 AB 边上的高,BE 平分∠ABC, 交 CD 于点E.若 BC=16,DE=
6,则△BCE的面积为 ( ) A.36 B.48 C.60 D.72
7.三条公路将A,B,C 三个村庄连成一个如图的三角形区域,如果在这个区域内修 建一个集贸市场,使集贸市场到三条公路的距离相等,那么这个集贸市场应建的 位置是 ( )
A. 三条高线的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
第7题图 第8题图
8. 如图,在△ABC 中 ,AB=AC,∠A=36°,D,E 两点分别在边 AC,BC 上 ,BD 平 分 ∠ABC,DE//AB. 图中的等腰三角形共有 ( ) A.3 个 B.4 个 C.5 个 D.6 个
9.如图,在△ABC 中,∠B=90°,分别以点A 和点 C 为圆心,以大于的长为半径作 弧,两弧相交于点M 和点N, 作直线MN, 分别交AB,AC于点E 和点F. 若 BC=3,AB= 9,则BE 的长为 ( ) A.3 B.4 C.5 D.6
第9题图 第10题图
10.如图,已知在等边三角形ABC 中 ,AD⊥BC,AD=8 √3.若点P 在线段AD 上运动,则 的最小值为 ( ) A.4√3 B.8√3 C.10 D.12
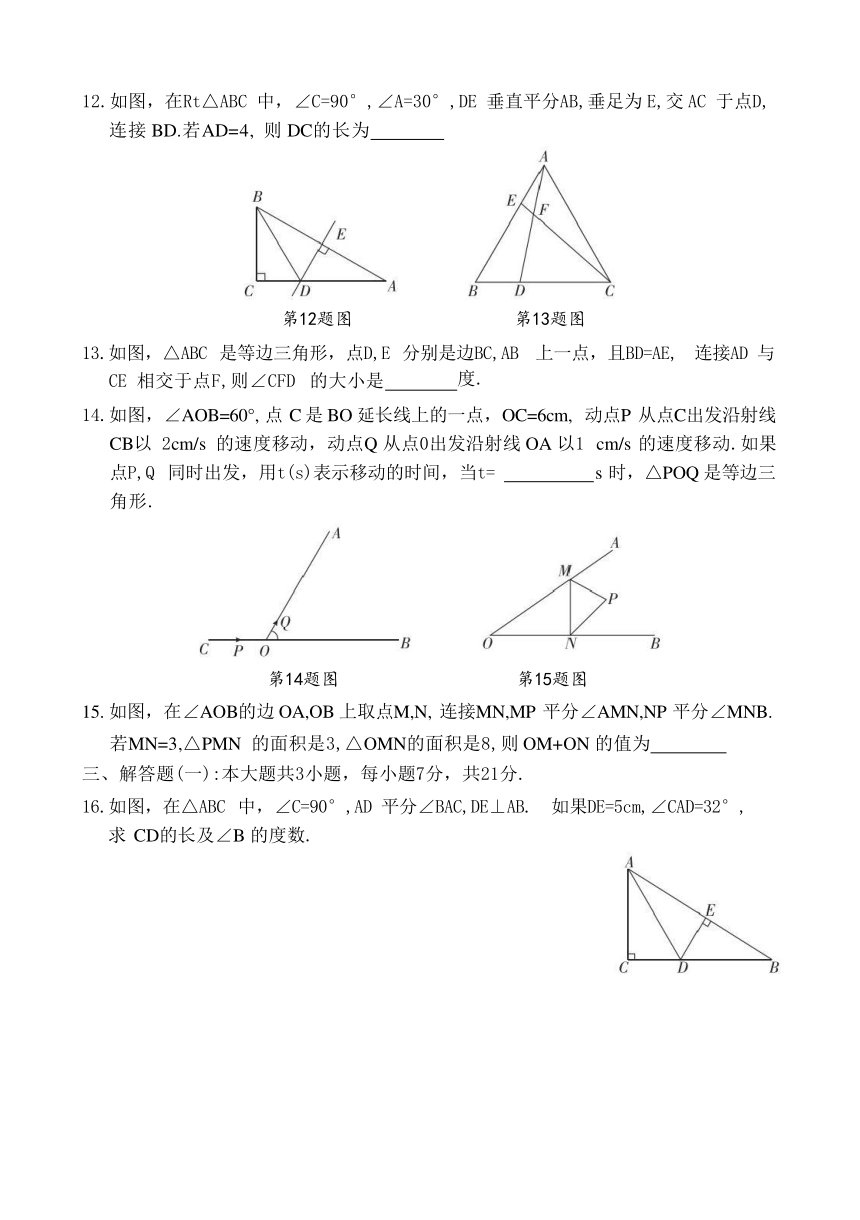
二、填空题:本大题共5小题,每小题3分,共15分.
11.命题“直角三角形的两个锐角互余”的逆命题是 命题(填“真”或“假”).
12.如图,在Rt△ABC 中,∠C=90°,∠A=30°,DE 垂直平分AB,垂足为 E,交 AC 于点D, 连接 BD.若AD=4, 则 DC的长为
第12题图
第13题图
13.如图,△ABC 是等边三角形,点D,E 分别是边BC,AB 上一点,且BD=AE, 连接AD 与 CE 相交于点F,则∠CFD 的大小是 度.
14.如图,∠AOB=60°, 点 C 是 BO 延长线上的一点,OC=6cm, 动点P 从点C出发沿射线 CB以 2cm/s 的速度移动,动点Q 从点0出发沿射线 OA 以1 cm/s 的速度移动.如果 点P,Q 同时出发,用t(s)表示移动的时间,当t= s 时,△POQ 是等边三 角形.
第14题图
第15题图
15. 如图,在∠AOB的边 OA,OB 上取点M,N, 连接MN,MP 平分∠AMN,NP 平分∠MNB. 若MN=3,△PMN 的面积是3,△OMN的面积是8,则 OM+ON 的值为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,DE⊥AB. 如果DE=5cm,∠CAD=32°, 求 CD的长及∠B 的度数.
17.如图,电信部门要在S 区修建一座发射塔P. 按照设计要求,发射塔P 到两个城镇A, B的距离必须相等,到两条高速公路m,n 的距离也必须相等,发射塔P 应建在什么位 置 在图上标出它的位置(尺规作图:只保留作图痕迹,不写作法).
18.如图,某港口P 位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口, 各自沿一固定方向航行,“远航”号每小时航行20n mile,“海天”号每小时航行15n mile, 它们离开港口两个小时后相距50n mile.如果知道“远航”号沿东北方向航行,请求出 “海天”号沿哪个方向航行.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19. 如图,在△ABC中 ,AB=AC=10,BC=12,M 为 BC 的中点,MN⊥AC 于 点N. 求 MN
的长.
20. 如图,已知AB⊥CF于点B,DE⊥CF 于点E,BH=EG,AH=DG,∠C=∠F.
(1)求证:△ ABH≌△DEG;
(2)求证:CE=FB.
21. 如图,在△ABC中 ,AE 是∠BAC的平分线,交BC于点E,DE//AB 交AC 于点D.
(1)求证:AD=DE;
(2)若AC=AB,DE=3, 求 AC的长.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,已知E 是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D 是垂足,连接CD,交 OE 于点F.
(1)求证:0E 是 CD的垂直平分线.
(2)若∠AOB=60°, 请你写出 OE,EF 之间的数量关系.并说明理由.
23.已知△ABC 是等边三角形,点D 是直线BC 上一点,以AD 为一边在AD的右侧作等边 三角形 ADE.
(1)如图①,点D 在线段BC 上移动时,直接写出∠BAD 和∠CAE的大小关系;
(2)如图②、图③,点D 在线段BC ( 或CB) 的延长线上移动时,猜想∠DCE 的大小是 否发生变化.若不变,请求出其大小;若变化,请说明理由.
图① 图② 图③
第一章检测卷
1.B 2.D 3.B 4.C 5.D 6.B 7.C 8.C 9.B
10.B【 解析】如图,过点P 作 PH⊥AC 于点H, 过 点B 作 BK⊥AC于点K.
∵△ABC是等边三角形,AD⊥BC,
∵BK⊥AC, ∴BK=AD=8√3.
∵PH⊥AC, ∴
∵PB+PH≥BK=,
的最小值为.
11.真 1 2 . 2 13.6014.6
15.11【解析】如图,过点 P 作 PE⊥OB, 垂足为E, 过点P 作 PF⊥MN, 垂足为F, 过点P 作 PG⊥OA,垂足为 G, 连
接OP.
∵P 是△MON外角平分线 的交点,
∴PF=PG=PE.
∵MN=3,S△PMN=3,
∴PF=2. ∴PG=PE=2.
∵S△OMN=8,∴S△OMp+S△Np-S△PMN=8.
∴OM+ON=11.
16. 解:∵ AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE=5cm,∠BAC=2∠CAD=2×32°=64° . ∴∠B=90°-∠BAC=90°-64°=26°.
17.解:如图,点P 即为所求.
18. 解:由题意,可得RP=2×15=30(n mile),PQ=2×20=40(n mile),QR=50n mile.
∵30 +40 =50 , ∴RP +PQ =QR .
∴△RPQ 是直角三角形.
∴∠RPQ=90°.
∵“远航”号沿东北方向航行, ∴∠QPS=45°.
∴∠RPS=∠RPQ-∠QPS=45°.
∴“海天”号沿西北方向航行.
19.解:如图,连接AM
∵AB=AC=10,BC=12,M为 BC 中点,
在 Rt△AMC 中,由勾股定理, 得AM= = =8.
20. 证明:(1)∵AB⊥CF,DE⊥CF, ∴∠DEG=∠ABH=90°
在Rt△ABH 和 Rt△DEG中 ,
∴Rt△ABH≌Rt△DEG(HL).
(2)∵Rt△ABH≌Rt△DEG(HL), ∴AB=DE.
在△ABC和△DEF 中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-BE=EF-BE.
∴CE=FB.
21.(1)证明:∵AE 是∠BAC的平分线, ∴∠DAE=∠BAE.
.∵DE//AB, ∴∠DEA=∠BAE.
∴∠DAE=∠DEA. ∴AD=DE.
(2)解:∵ AC=AB,AE是∠BAC的平分线,
∴AE⊥BC.
∴∠C+∠DAE=90°,∠CED+∠DEA=90°.
∴∠C=∠CED. ∴CD=DE.
∵DE=3, ∴AD=DE=CD=3. ∴AC=6.
22. (1)证明:∵ E 是∠AOB 的平分线上一 点,EC⊥OB, ED⊥OA,
∴DE=CE,
又∵ OE=OE, ∴Rt△ODE≌Rt△OCE(HL).
∴OD=OC.∴△DOC 是等腰三角形.
∵OE 是∠AOB的平分线,
∴OE⊥CD,DF=CF.
∴OE 是 CD的垂直平分线.
(2)解:0E=4EF. 理由如下:
∵OE 是∠AOB的平分线上一点,∠AOB=60°, ∴∠AOE=∠BOE=30°.
∵ED⊥OA,OE⊥CD,
∴OE=2DE,∠ODF=60°.
∴∠EDF=90°-60°=30° .
∴DE=2EF. ∴OE=4EF.
23. 解:(1)∠BAD=∠CAE.
(2)∠DCE 的大小不发生变化.理由如下:
当点D 在线段BC 的延长线上移动时,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=∠ACB=60°. ∴∠BAD=∠CAE.
在△BAD和△CAE中
∴△BAD≌△CAE(SAS). ∴∠B=∠ACE=60°.
∴∠DCE=180°-∠ACB-∠ACE=60°.
当点D 在线段CB的延长线上移动时,
∵△ABC和△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AD=AE,AB=AC. ∴∠ABD=120°,∠BAD=∠CAE.
在△BAD 和△CAE中
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE=120°.
∴∠DCE=∠ACE-∠ACB=120°-60°=60°.
综上所述,∠DCE=60°, 即∠DCE的大小不发生变化.
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.在等腰三角形ABC中 ,AB=AC,若∠A=70°, 则∠B 的度数是 ( ) A.40° B.55° C.65° D.60°
2.下列判定直角三角形全等的方法,错误的是 ( )
A. 两条直角边对应相等 B. 斜边和一锐角对应相等
C. 斜边和一直角边对应相等 D. 两锐角相等
3.用反证法证明命题“在△ABC 中,若AB=AC, 则∠B<90°”时,第一步应该假设( )
A. ∠B>90° B. ∠B≥90°
C.AB≠AC D.AB≠AC 且∠B≥90°
4.如图,直线m//n,△ABC 是等边三角形,顶点B 在直线n 上,直线m 交 AB 于点E,交AC 于点F. 若∠1=140°,则∠2的度数是 ( ) A.110° B.105° C.100° D.95°
第4题图 第5题图 第6题图
5. 如图,在△ABC 中 ,AB=AC,AD 是△ABC的角平分线 .若 AB=13,AD=12, 则 BC 的长为 ( ) A.6 B.5 C.8 D.10
6.如图,在△ABC 中 ,CD 是 AB 边上的高,BE 平分∠ABC, 交 CD 于点E.若 BC=16,DE=
6,则△BCE的面积为 ( ) A.36 B.48 C.60 D.72
7.三条公路将A,B,C 三个村庄连成一个如图的三角形区域,如果在这个区域内修 建一个集贸市场,使集贸市场到三条公路的距离相等,那么这个集贸市场应建的 位置是 ( )
A. 三条高线的交点 B. 三条中线的交点
C. 三条角平分线的交点 D. 三边垂直平分线的交点
第7题图 第8题图
8. 如图,在△ABC 中 ,AB=AC,∠A=36°,D,E 两点分别在边 AC,BC 上 ,BD 平 分 ∠ABC,DE//AB. 图中的等腰三角形共有 ( ) A.3 个 B.4 个 C.5 个 D.6 个
9.如图,在△ABC 中,∠B=90°,分别以点A 和点 C 为圆心,以大于的长为半径作 弧,两弧相交于点M 和点N, 作直线MN, 分别交AB,AC于点E 和点F. 若 BC=3,AB= 9,则BE 的长为 ( ) A.3 B.4 C.5 D.6
第9题图 第10题图
10.如图,已知在等边三角形ABC 中 ,AD⊥BC,AD=8 √3.若点P 在线段AD 上运动,则 的最小值为 ( ) A.4√3 B.8√3 C.10 D.12
二、填空题:本大题共5小题,每小题3分,共15分.
11.命题“直角三角形的两个锐角互余”的逆命题是 命题(填“真”或“假”).
12.如图,在Rt△ABC 中,∠C=90°,∠A=30°,DE 垂直平分AB,垂足为 E,交 AC 于点D, 连接 BD.若AD=4, 则 DC的长为
第12题图
第13题图
13.如图,△ABC 是等边三角形,点D,E 分别是边BC,AB 上一点,且BD=AE, 连接AD 与 CE 相交于点F,则∠CFD 的大小是 度.
14.如图,∠AOB=60°, 点 C 是 BO 延长线上的一点,OC=6cm, 动点P 从点C出发沿射线 CB以 2cm/s 的速度移动,动点Q 从点0出发沿射线 OA 以1 cm/s 的速度移动.如果 点P,Q 同时出发,用t(s)表示移动的时间,当t= s 时,△POQ 是等边三 角形.
第14题图
第15题图
15. 如图,在∠AOB的边 OA,OB 上取点M,N, 连接MN,MP 平分∠AMN,NP 平分∠MNB. 若MN=3,△PMN 的面积是3,△OMN的面积是8,则 OM+ON 的值为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.如图,在△ABC 中,∠C=90°,AD 平分∠BAC,DE⊥AB. 如果DE=5cm,∠CAD=32°, 求 CD的长及∠B 的度数.
17.如图,电信部门要在S 区修建一座发射塔P. 按照设计要求,发射塔P 到两个城镇A, B的距离必须相等,到两条高速公路m,n 的距离也必须相等,发射塔P 应建在什么位 置 在图上标出它的位置(尺规作图:只保留作图痕迹,不写作法).
18.如图,某港口P 位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口, 各自沿一固定方向航行,“远航”号每小时航行20n mile,“海天”号每小时航行15n mile, 它们离开港口两个小时后相距50n mile.如果知道“远航”号沿东北方向航行,请求出 “海天”号沿哪个方向航行.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19. 如图,在△ABC中 ,AB=AC=10,BC=12,M 为 BC 的中点,MN⊥AC 于 点N. 求 MN
的长.
20. 如图,已知AB⊥CF于点B,DE⊥CF 于点E,BH=EG,AH=DG,∠C=∠F.
(1)求证:△ ABH≌△DEG;
(2)求证:CE=FB.
21. 如图,在△ABC中 ,AE 是∠BAC的平分线,交BC于点E,DE//AB 交AC 于点D.
(1)求证:AD=DE;
(2)若AC=AB,DE=3, 求 AC的长.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.如图,已知E 是∠AOB的平分线上一点,EC⊥OB,ED⊥OA,C,D 是垂足,连接CD,交 OE 于点F.
(1)求证:0E 是 CD的垂直平分线.
(2)若∠AOB=60°, 请你写出 OE,EF 之间的数量关系.并说明理由.
23.已知△ABC 是等边三角形,点D 是直线BC 上一点,以AD 为一边在AD的右侧作等边 三角形 ADE.
(1)如图①,点D 在线段BC 上移动时,直接写出∠BAD 和∠CAE的大小关系;
(2)如图②、图③,点D 在线段BC ( 或CB) 的延长线上移动时,猜想∠DCE 的大小是 否发生变化.若不变,请求出其大小;若变化,请说明理由.
图① 图② 图③
第一章检测卷
1.B 2.D 3.B 4.C 5.D 6.B 7.C 8.C 9.B
10.B【 解析】如图,过点P 作 PH⊥AC 于点H, 过 点B 作 BK⊥AC于点K.
∵△ABC是等边三角形,AD⊥BC,
∵BK⊥AC, ∴BK=AD=8√3.
∵PH⊥AC, ∴
∵PB+PH≥BK=,
的最小值为.
11.真 1 2 . 2 13.6014.6
15.11【解析】如图,过点 P 作 PE⊥OB, 垂足为E, 过点P 作 PF⊥MN, 垂足为F, 过点P 作 PG⊥OA,垂足为 G, 连
接OP.
∵P 是△MON外角平分线 的交点,
∴PF=PG=PE.
∵MN=3,S△PMN=3,
∴PF=2. ∴PG=PE=2.
∵S△OMN=8,∴S△OMp+S△Np-S△PMN=8.
∴OM+ON=11.
16. 解:∵ AD平分∠BAC,DE⊥AB,DC⊥AC,
∴CD=DE=5cm,∠BAC=2∠CAD=2×32°=64° . ∴∠B=90°-∠BAC=90°-64°=26°.
17.解:如图,点P 即为所求.
18. 解:由题意,可得RP=2×15=30(n mile),PQ=2×20=40(n mile),QR=50n mile.
∵30 +40 =50 , ∴RP +PQ =QR .
∴△RPQ 是直角三角形.
∴∠RPQ=90°.
∵“远航”号沿东北方向航行, ∴∠QPS=45°.
∴∠RPS=∠RPQ-∠QPS=45°.
∴“海天”号沿西北方向航行.
19.解:如图,连接AM
∵AB=AC=10,BC=12,M为 BC 中点,
在 Rt△AMC 中,由勾股定理, 得AM= = =8.
20. 证明:(1)∵AB⊥CF,DE⊥CF, ∴∠DEG=∠ABH=90°
在Rt△ABH 和 Rt△DEG中 ,
∴Rt△ABH≌Rt△DEG(HL).
(2)∵Rt△ABH≌Rt△DEG(HL), ∴AB=DE.
在△ABC和△DEF 中,
∴△ABC≌△DEF(AAS).
∴BC=EF.
∴BC-BE=EF-BE.
∴CE=FB.
21.(1)证明:∵AE 是∠BAC的平分线, ∴∠DAE=∠BAE.
.∵DE//AB, ∴∠DEA=∠BAE.
∴∠DAE=∠DEA. ∴AD=DE.
(2)解:∵ AC=AB,AE是∠BAC的平分线,
∴AE⊥BC.
∴∠C+∠DAE=90°,∠CED+∠DEA=90°.
∴∠C=∠CED. ∴CD=DE.
∵DE=3, ∴AD=DE=CD=3. ∴AC=6.
22. (1)证明:∵ E 是∠AOB 的平分线上一 点,EC⊥OB, ED⊥OA,
∴DE=CE,
又∵ OE=OE, ∴Rt△ODE≌Rt△OCE(HL).
∴OD=OC.∴△DOC 是等腰三角形.
∵OE 是∠AOB的平分线,
∴OE⊥CD,DF=CF.
∴OE 是 CD的垂直平分线.
(2)解:0E=4EF. 理由如下:
∵OE 是∠AOB的平分线上一点,∠AOB=60°, ∴∠AOE=∠BOE=30°.
∵ED⊥OA,OE⊥CD,
∴OE=2DE,∠ODF=60°.
∴∠EDF=90°-60°=30° .
∴DE=2EF. ∴OE=4EF.
23. 解:(1)∠BAD=∠CAE.
(2)∠DCE 的大小不发生变化.理由如下:
当点D 在线段BC 的延长线上移动时,
∵△ABC和△ADE是等边三角形,
∴AB=AC,AD=AE,∠BAC=∠DAE=∠B=∠ACB=60°. ∴∠BAD=∠CAE.
在△BAD和△CAE中
∴△BAD≌△CAE(SAS). ∴∠B=∠ACE=60°.
∴∠DCE=180°-∠ACB-∠ACE=60°.
当点D 在线段CB的延长线上移动时,
∵△ABC和△ADE是等边三角形,
∴∠DAE=∠BAC=∠ABC=∠ACB=60°,AD=AE,AB=AC. ∴∠ABD=120°,∠BAD=∠CAE.
在△BAD 和△CAE中
∴△BAD≌△CAE(SAS).
∴∠ABD=∠ACE=120°.
∴∠DCE=∠ACE-∠ACB=120°-60°=60°.
综上所述,∠DCE=60°, 即∠DCE的大小不发生变化.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
