第二章 一元一次不等式与一元一次不等式组 检测卷 (含答案)2024-2025学年北师版数学八年级下册
文档属性
| 名称 | 第二章 一元一次不等式与一元一次不等式组 检测卷 (含答案)2024-2025学年北师版数学八年级下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 200.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 13:20:17 | ||
图片预览



文档简介
第二章 一元一次不等式与一元一次不等式组 检测卷
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列各式中,属于不等式的是 ( ) A.2a-b B.x≠0 C.x-1=0 D.y=x+1
2.不等式x+2>3 的解集是 ( ) A.x<1 B.x<5 C.x>1 D.x>5
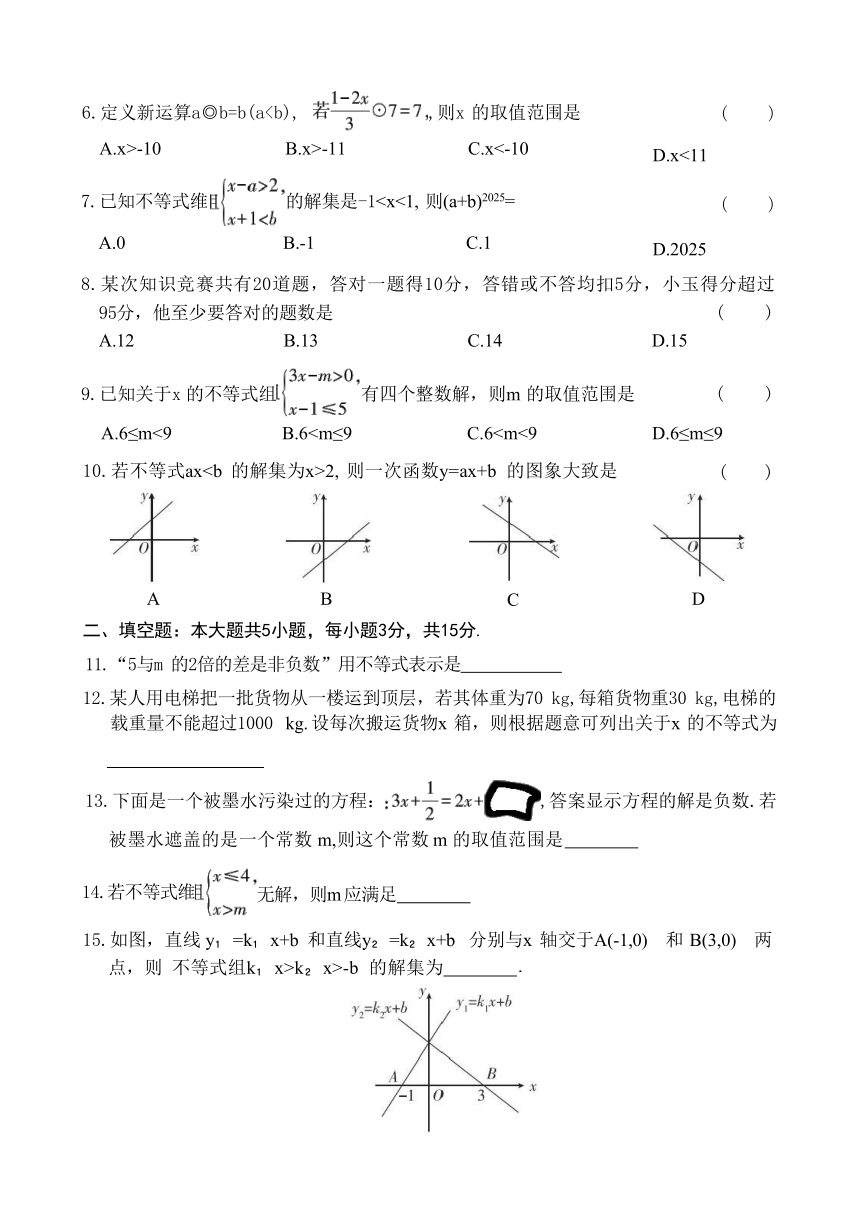
3.如图表示的不等式组的解集是 ( )
(
-4
-3
-2
-1
0
1
2
3
)
A B. C. D.
4.根据图象,可得关于x 的不等式kx>-x+3 的解集是 ( )
A.x<2 B.x>2 C.x<1 D.x>1
5.下列说法一定正确的是 ( )
A. 若 ac =bc , 则 a=b B. 若 ac>bc(c>0), 则 aC. 若 a>b, 则ac >bc D. 若 a6.定义新运算a◎b=b(a-10 B.x>-11 C.x<-10
7.已知不等式维 的解集是-1( )
D.x<11
( )
D.2025
8.某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过 95分,他至少要答对的题数是 ( ) A.12 B.13 C.14 D.15
9.已知关于x 的不等式组有四个整数解,则m 的取值范围是 ( ) A.6≤m<9 B.610.若不等式ax2, 则一次函数y=ax+b 的图象大致是 ( )
A B C D
二、填空题:本大题共5小题,每小题3分,共15分.
11.“5与m 的2倍的差是非负数”用不等式表示是
12.某人用电梯把一批货物从一楼运到顶层,若其体重为70 kg,每箱货物重30 kg,电梯的 载重量不能超过1000 kg. 设每次搬运货物x 箱,则根据题意可列出关于x 的不等式为
13.下面是一个被墨水污染过的方程:,答案显示方程的解是负数.若 被墨水遮盖的是一个常数 m,则这个常数 m 的取值范围是
14.若不等式维无解,则m 应满足
15.如图,直线 y =k x+b 和直线y =k x+b 分别与x 轴交于A(-1,0) 和 B(3,0) 两点,则 不等式组k x>k x>-b 的解集为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.下面是小明同学解不等式的过程:
解:去分母,得x+5-1<3x+2.……①
移项、合并同类项,得-2x<-2.……②
两边都除以-2,得x>1.……③
小明第 步出错;请写出正确的求解过程.
17.求不等式组的整数解.
18.解不等式组并在数轴上表示出它的解集.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.整式的值为P.
(1)当m=2 时,求P 的值;
(2)若P 的取值范围如图所示,求m 的负整数值.
20.已知关于x,y 的方程
(1)若方程组的解满足-3≤x+y<7,求 a 的取值范围;
(2)在(1)的条件下,化简 a|-2|+2|a+3|.
21.如图,在平面直角坐标系xOy 中,直线l :y=kx+b(k≠0) 与直线l :y=mx+n(m≠0) 相 交于点P, 与x 轴、y 轴分别交于A,B 两点.
(1)若点A,B,P 的坐标分别为(1,0),(0,3),(3,-2),直接写出下列各小题的答案.
①方程kx+b=0 的解是 ;②方程的解是 ;
③不等式kx+b(2)若点A,B 的坐标分别为(1,0),(0,2),直线l 的表达式为y=2x-6, 连接 OP, 求△BOP的面积.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22. 某快递企业为提高工作效率,拟购买A,B 两种型号的智能机器人进行快递分拣.
相关信息如下: 信息一
A型机器人台数 B型机器人台数 总费用/万元
1 3 260
3 2 360
信息二
A型机器人每台每天可
分拣快递22万件;
B型机器人每台每天可
分拣快递18万件.
(1)求 A,B 两种型号智能机器人的单价.
(2)现该企业准备用不超过700万元购买 A,B 两种型号智能机器人共10台,则该企 业如何购买才能使每天分拣快递的件数最多
23. 【背景】如图①是某品牌的饮水机,此饮水机有开水、温水两个按钮,图②为其信息图.
开水 开水 水流速度
15mL/s
100℃
温水
30℃
温水
水流速度
20mL/s
图① 图②
【主题】如何接到最佳温度的温水.
【素材】温水水流速度是20 mL/s;
水杯容积:700 mL;
物理知识:开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量, 即开水体积×开水降低的温度=温水体积×温水升高的温度;
生活经验:饮水最佳温度是35~38℃(包括35℃与38℃),这 一 温度最接近人体 体温 .
【操作】先从饮水机接温水 xs, 再接开水,直至接满700 mL 的水杯为止(备注:接水期 间不计热损失,不考虑水溢出的情况).
【 问 题 】
(1)接到温水的体积是 mL, 接到开水的体积是 mL( 用 含x 的 代数式表示).
(2)若所接的温水的体积不少于开水体积的2倍,则至少应接温水多少秒
(3)若水杯接满水后,水杯中温度是50℃,求x 的值 .
(4)记水杯接满水后,水杯中温度为y℃, 则 y 关 于x 的关系式是 ; 若要使杯中温度达到最佳水温,则x 的取值范围是
第二章检测卷
1.B 2.C 3.D 4.D 5.D 6.A 7.B 8.C 9.A
10.D 11.5-2m≥0 12.30x+70≤1000 13.
14.m≥4 15.016.解:①
去分母,得x+5-2<3x+2 移项、合并同类项,得-2x<-1. 两边都除以-2,得
17.解:由x-1≥1-x, 得 x≥1.
由x+8>4x-1, 得 x<3.
∴原不等式组的解集为1≤x<3.
∴不等式组的整数解为1,2.
18.解:解不等式①,得x>-2.
解不等式②,得x≤3.
∴该不等式组的解集为-2将该不等式组的解集在数轴上表示如图所示.
19.解:(1)根据题意,得
(2)由数轴知P≤7, 即 3 ,解得m≥-2. ∴m 的负整数值为-1,-2.
20.解:(1)
①+②,得3x=6a+3. 解得 x=2a+1.
把x=2a+1 代入①,得2a+1-y=3. 解得y=2a-2.
∵-3≤x+y<7,
∴-3≤2a+1+2a-2<7. 解得
∴a 的取值范围
(2) , ∴a-2<0,a+3>0. ∴|a-2|+2|a+3|=2-a+2(a+3)=a+8.
21.解:(1)①x=1 ③x>3 ④x≤0
(2)如图.
把(1,0),(0,2)代入y=kx+b,
解得
∴直线l 的函数解析式为y=-2x+2.
联立,得 解得
∴P(2,-2).
22.解:(1)设A 型智能机器人的单价为x 万元,B型智能机 器人的单价为y 万元.
根据题意,得 解得
答 :A型智能机器人的单价为80万元,B 型智能机器人 的单价为60万元.
(2)设购买A 型智能机器人a 台,则购买B 型智能机器 人(10-a) 台.
根据题意,得80a+60(10-a)≤700. 解得a≤5.
设每天分拣快递s 万件,则s=22a+18(10-a)=4a+180.
∵4>0,∴s 随 a的增大而增大.
∴ 当a=5 时,s有最大值,即此时每天分拣快递的件数最多. ∴选择购买A 型智能机器人5台,购买B型智能机器人5台 .
23. 解:(1)20x(700-20x)
(2)根据题意,得温水的体积是20x mL,开水的体积为 (700-20x)mL.
∵所接的温水的体积不少于开水体积的2倍, ∴20x≥2(700-20x).
解得
∴至少应接温
(3)当水杯中温度是50℃时,开水降低的温度为100-50=50(℃),温水升高的温度为50-30=20(℃).
根据题意,得(700-20x)×50=20×20x. 解得x=25.
(4)y=-2x+100 31≤x≤32.5
[提示]当水杯中温度是y℃时,开水降低的温度为 (100-y)℃,
温水升高的温度为(y-30)℃.
根据题意,得(700-20x)(100-y)=20x(y-30).
整理得y=-2x+100.
若要使杯中温度达到最佳水温35~38℃,则有35≤y≤38, 代入y=-2x+100,
得35≤-2x+100≤38.
解得31≤x≤32.5.
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列各式中,属于不等式的是 ( ) A.2a-b B.x≠0 C.x-1=0 D.y=x+1
2.不等式x+2>3 的解集是 ( ) A.x<1 B.x<5 C.x>1 D.x>5
3.如图表示的不等式组的解集是 ( )
(
-4
-3
-2
-1
0
1
2
3
)
A B. C. D.
4.根据图象,可得关于x 的不等式kx>-x+3 的解集是 ( )
A.x<2 B.x>2 C.x<1 D.x>1
5.下列说法一定正确的是 ( )
A. 若 ac =bc , 则 a=b B. 若 ac>bc(c>0), 则 a
7.已知不等式维 的解集是-1
D.x<11
( )
D.2025
8.某次知识竞赛共有20道题,答对一题得10分,答错或不答均扣5分,小玉得分超过 95分,他至少要答对的题数是 ( ) A.12 B.13 C.14 D.15
9.已知关于x 的不等式组有四个整数解,则m 的取值范围是 ( ) A.6≤m<9 B.6
A B C D
二、填空题:本大题共5小题,每小题3分,共15分.
11.“5与m 的2倍的差是非负数”用不等式表示是
12.某人用电梯把一批货物从一楼运到顶层,若其体重为70 kg,每箱货物重30 kg,电梯的 载重量不能超过1000 kg. 设每次搬运货物x 箱,则根据题意可列出关于x 的不等式为
13.下面是一个被墨水污染过的方程:,答案显示方程的解是负数.若 被墨水遮盖的是一个常数 m,则这个常数 m 的取值范围是
14.若不等式维无解,则m 应满足
15.如图,直线 y =k x+b 和直线y =k x+b 分别与x 轴交于A(-1,0) 和 B(3,0) 两点,则 不等式组k x>k x>-b 的解集为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.下面是小明同学解不等式的过程:
解:去分母,得x+5-1<3x+2.……①
移项、合并同类项,得-2x<-2.……②
两边都除以-2,得x>1.……③
小明第 步出错;请写出正确的求解过程.
17.求不等式组的整数解.
18.解不等式组并在数轴上表示出它的解集.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.整式的值为P.
(1)当m=2 时,求P 的值;
(2)若P 的取值范围如图所示,求m 的负整数值.
20.已知关于x,y 的方程
(1)若方程组的解满足-3≤x+y<7,求 a 的取值范围;
(2)在(1)的条件下,化简 a|-2|+2|a+3|.
21.如图,在平面直角坐标系xOy 中,直线l :y=kx+b(k≠0) 与直线l :y=mx+n(m≠0) 相 交于点P, 与x 轴、y 轴分别交于A,B 两点.
(1)若点A,B,P 的坐标分别为(1,0),(0,3),(3,-2),直接写出下列各小题的答案.
①方程kx+b=0 的解是 ;②方程的解是 ;
③不等式kx+b
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22. 某快递企业为提高工作效率,拟购买A,B 两种型号的智能机器人进行快递分拣.
相关信息如下: 信息一
A型机器人台数 B型机器人台数 总费用/万元
1 3 260
3 2 360
信息二
A型机器人每台每天可
分拣快递22万件;
B型机器人每台每天可
分拣快递18万件.
(1)求 A,B 两种型号智能机器人的单价.
(2)现该企业准备用不超过700万元购买 A,B 两种型号智能机器人共10台,则该企 业如何购买才能使每天分拣快递的件数最多
23. 【背景】如图①是某品牌的饮水机,此饮水机有开水、温水两个按钮,图②为其信息图.
开水 开水 水流速度
15mL/s
100℃
温水
30℃
温水
水流速度
20mL/s
图① 图②
【主题】如何接到最佳温度的温水.
【素材】温水水流速度是20 mL/s;
水杯容积:700 mL;
物理知识:开水和温水混合时会发生热传递,开水放出的热量等于温水吸收的热量, 即开水体积×开水降低的温度=温水体积×温水升高的温度;
生活经验:饮水最佳温度是35~38℃(包括35℃与38℃),这 一 温度最接近人体 体温 .
【操作】先从饮水机接温水 xs, 再接开水,直至接满700 mL 的水杯为止(备注:接水期 间不计热损失,不考虑水溢出的情况).
【 问 题 】
(1)接到温水的体积是 mL, 接到开水的体积是 mL( 用 含x 的 代数式表示).
(2)若所接的温水的体积不少于开水体积的2倍,则至少应接温水多少秒
(3)若水杯接满水后,水杯中温度是50℃,求x 的值 .
(4)记水杯接满水后,水杯中温度为y℃, 则 y 关 于x 的关系式是 ; 若要使杯中温度达到最佳水温,则x 的取值范围是
第二章检测卷
1.B 2.C 3.D 4.D 5.D 6.A 7.B 8.C 9.A
10.D 11.5-2m≥0 12.30x+70≤1000 13.
14.m≥4 15.0
去分母,得x+5-2<3x+2 移项、合并同类项,得-2x<-1. 两边都除以-2,得
17.解:由x-1≥1-x, 得 x≥1.
由x+8>4x-1, 得 x<3.
∴原不等式组的解集为1≤x<3.
∴不等式组的整数解为1,2.
18.解:解不等式①,得x>-2.
解不等式②,得x≤3.
∴该不等式组的解集为-2
19.解:(1)根据题意,得
(2)由数轴知P≤7, 即 3 ,解得m≥-2. ∴m 的负整数值为-1,-2.
20.解:(1)
①+②,得3x=6a+3. 解得 x=2a+1.
把x=2a+1 代入①,得2a+1-y=3. 解得y=2a-2.
∵-3≤x+y<7,
∴-3≤2a+1+2a-2<7. 解得
∴a 的取值范围
(2) , ∴a-2<0,a+3>0. ∴|a-2|+2|a+3|=2-a+2(a+3)=a+8.
21.解:(1)①x=1 ③x>3 ④x≤0
(2)如图.
把(1,0),(0,2)代入y=kx+b,
解得
∴直线l 的函数解析式为y=-2x+2.
联立,得 解得
∴P(2,-2).
22.解:(1)设A 型智能机器人的单价为x 万元,B型智能机 器人的单价为y 万元.
根据题意,得 解得
答 :A型智能机器人的单价为80万元,B 型智能机器人 的单价为60万元.
(2)设购买A 型智能机器人a 台,则购买B 型智能机器 人(10-a) 台.
根据题意,得80a+60(10-a)≤700. 解得a≤5.
设每天分拣快递s 万件,则s=22a+18(10-a)=4a+180.
∵4>0,∴s 随 a的增大而增大.
∴ 当a=5 时,s有最大值,即此时每天分拣快递的件数最多. ∴选择购买A 型智能机器人5台,购买B型智能机器人5台 .
23. 解:(1)20x(700-20x)
(2)根据题意,得温水的体积是20x mL,开水的体积为 (700-20x)mL.
∵所接的温水的体积不少于开水体积的2倍, ∴20x≥2(700-20x).
解得
∴至少应接温
(3)当水杯中温度是50℃时,开水降低的温度为100-50=50(℃),温水升高的温度为50-30=20(℃).
根据题意,得(700-20x)×50=20×20x. 解得x=25.
(4)y=-2x+100 31≤x≤32.5
[提示]当水杯中温度是y℃时,开水降低的温度为 (100-y)℃,
温水升高的温度为(y-30)℃.
根据题意,得(700-20x)(100-y)=20x(y-30).
整理得y=-2x+100.
若要使杯中温度达到最佳水温35~38℃,则有35≤y≤38, 代入y=-2x+100,
得35≤-2x+100≤38.
解得31≤x≤32.5.
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
