期末质量检测卷(一) (含答案)2024-2025学年北师版数学八年级下册
文档属性
| 名称 | 期末质量检测卷(一) (含答案)2024-2025学年北师版数学八年级下册 |  | |
| 格式 | docx | ||
| 文件大小 | 316.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 21:01:24 | ||
图片预览



文档简介
期末质量检测卷(一)
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列图形是中心对称图形的是 ( )
A.平行四边形 B. 直角三角形
C. 等边三角形 D.正五边形
2.已知a>b,下列式子成立的是 ( )
A.ac >bc B
C.-a>-b D.a >b
3.多项式a +1 与下列单项式的和不可以因式分解的是 ( ) A.-2a B.2a C.-2 D.3
4.若分的值为0,则x 的值为 ( ) A.±3 B.3 C.-3 D.0
5.下列命题中,错误的是 ( )
A. 正八边形的每个外角都等于45°
B. 一组对边相等且另一组对边平行的四边形是平行四边形
C. 点 P(a,b) 关于原点对称的点的坐标为P'(-a,-b)
D. 角平分线上的点到这个角两边的距离相等
6.如图,在△ABC 中 ,AB 的垂直平分线交AB 于点D,交 BC 于点 E,连接AE. 若 BC=6, AC=5, 则△ACE 的周长为 ( ) A.11 B.12 C.16 D.17
第6题图
第7题图
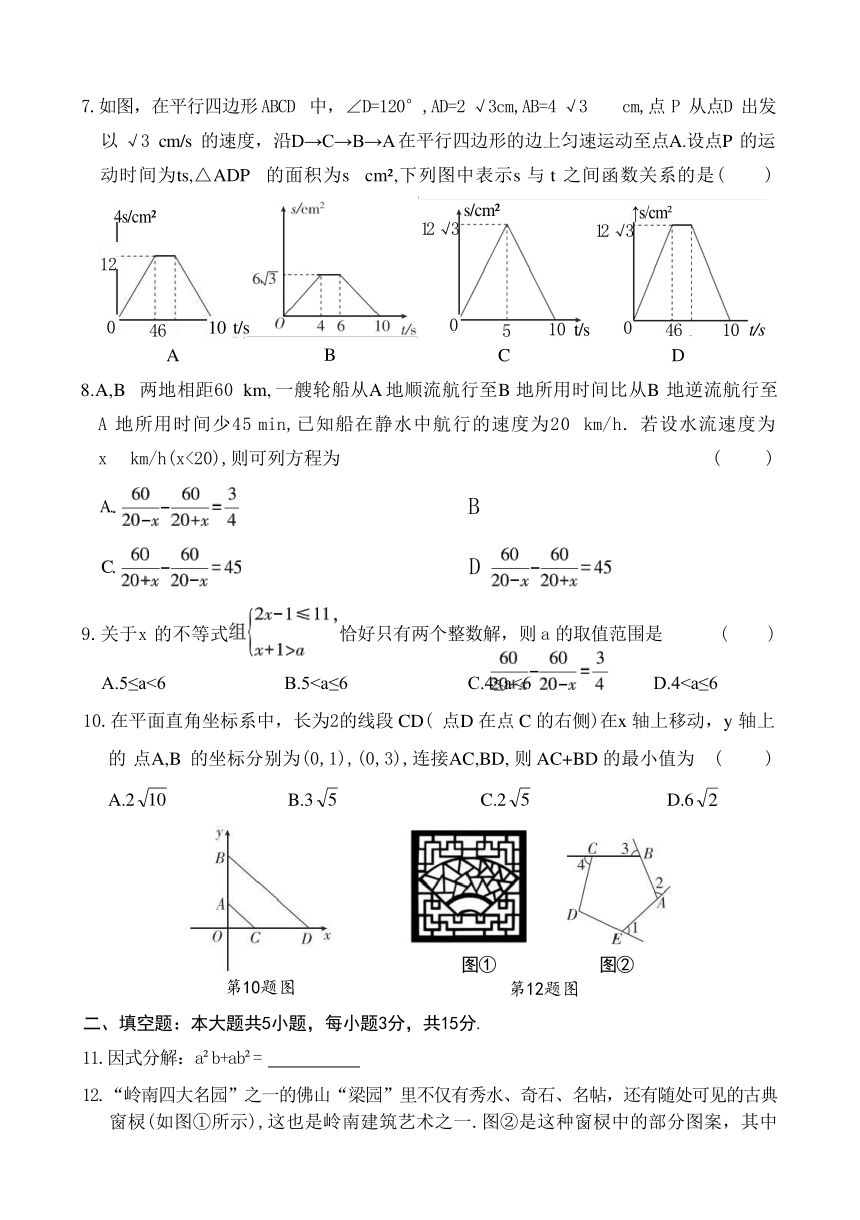
7.如图,在平行四边形 ABCD 中,∠D=120°,AD=2 √3cm,AB=4 √3 cm,点 P 从点D 出发 以 √3 cm/s 的速度,沿D→C→B→A 在平行四边形的边上匀速运动至点A.设点P 的运 动时间为ts,△ADP 的面积为s cm ,下列图中表示s 与 t 之间函数关系的是( )
(
4s/cm
) (
12
) (
0
46
) (
12
√3
10
t/s
0
10
t/s
0
46
10
t/s
↑s/cm
12
√3
s/cm
5
)
A B C D
8.A,B 两地相距60 km, 一艘轮船从A 地顺流航行至B 地所用时间比从B 地逆流航行至 A 地所用时间少45 min,已知船在静水中航行的速度为20 km/h. 若设水流速度为 x km/h(x<20),则可列方程为 ( )
A.
C.
9.关于x 的不等式
B
D
恰好只有两个整数解,则 a 的取值范围是
( )
A.5≤a<6 B.510.在平面直角坐标系中,长为2的线段 CD( 点D 在点 C 的右侧)在x 轴上移动,y 轴上 的 点A,B 的坐标分别为(0,1),(0,3),连接AC,BD, 则 AC+BD 的最小值为 ( ) A.2 B.3 C.2 D.6
图①
图②
第10题图 第12题图
二、填空题:本大题共5小题,每小题3分,共15分.
11.因式分解:a b+ab =
12.“岭南四大名园”之一的佛山“梁园”里不仅有秀水、奇石、名帖,还有随处可见的古典 窗棂(如图①所示),这也是岭南建筑艺术之一.图②是这种窗棂中的部分图案,其中
∠1,∠2,∠3,∠4是五边形ABCDE 的4个外角.若∠1+∠2+∠3+∠4=280°,则∠D 的度数是
13. 如图,已知△ABC的周长是15,0B,OC 分别平分∠ABC 和∠ACB,OD⊥BC于点D,且 OD=4, 则△ABC的面积是
第13题图
第15题图
14.小明4岁那年父亲种下一棵山毛榉和一棵枫树.当时山毛榉高3m, 枫树高1.8 m, 现 在枫树已经比山毛榉高了.在此期间,山毛榉的平均生长速度是每年长高0.15m, 枫 树的平均生长速度是每年长高0.3 m. 请问小明现在的年龄应该超过 岁.
15.如图,在平行四边形ABCD中 ,AB=4,沿对角线AC 翻折,点B 的对应点为B',B'C 与 AD交于点E, 此时△CDE 恰为等边三角形,则重叠部分(即图中阴影部分)的面积 为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.解方程
17.先化简再求值:,且x=2025.
18.如图,在△ABC 中 ,AB=AC,∠BAC=120°.
(1)尺规作图:作线段AB 的垂直平分线 DE, 交AB 于点E,交 BC 于点D (保留作图痕 迹,不写作法);
(2)求证:CD=2BD.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.阅读与思考:
在现今信息化时代,智能手机几乎人手必备,应用到了生活的各个领域,锁屏密码为 保护我们个人隐私起到了不可或缺的作用,而诸如“1234”、生日等简单密码又容易被 破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分 解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x -1 因 式分解的结果为(x-1)(x+1) 或(x+1)(x-1), 取个人年龄作为x 的值,当x=13时, x-1=12,x+1=14, 此时可以得到数字密码1214或1412.
(1)根据上述方法,若多项式为x +2x+1, 请你结合个人年龄设置一个锁屏密码,当 x=_ 时,锁屏密码为 ;
(2)若王老师选取的多项式为x -x,已知王老师手机的锁屏密码是6位数字353334, 请尝试分析王老师当前年龄是多少岁,并说明理由.
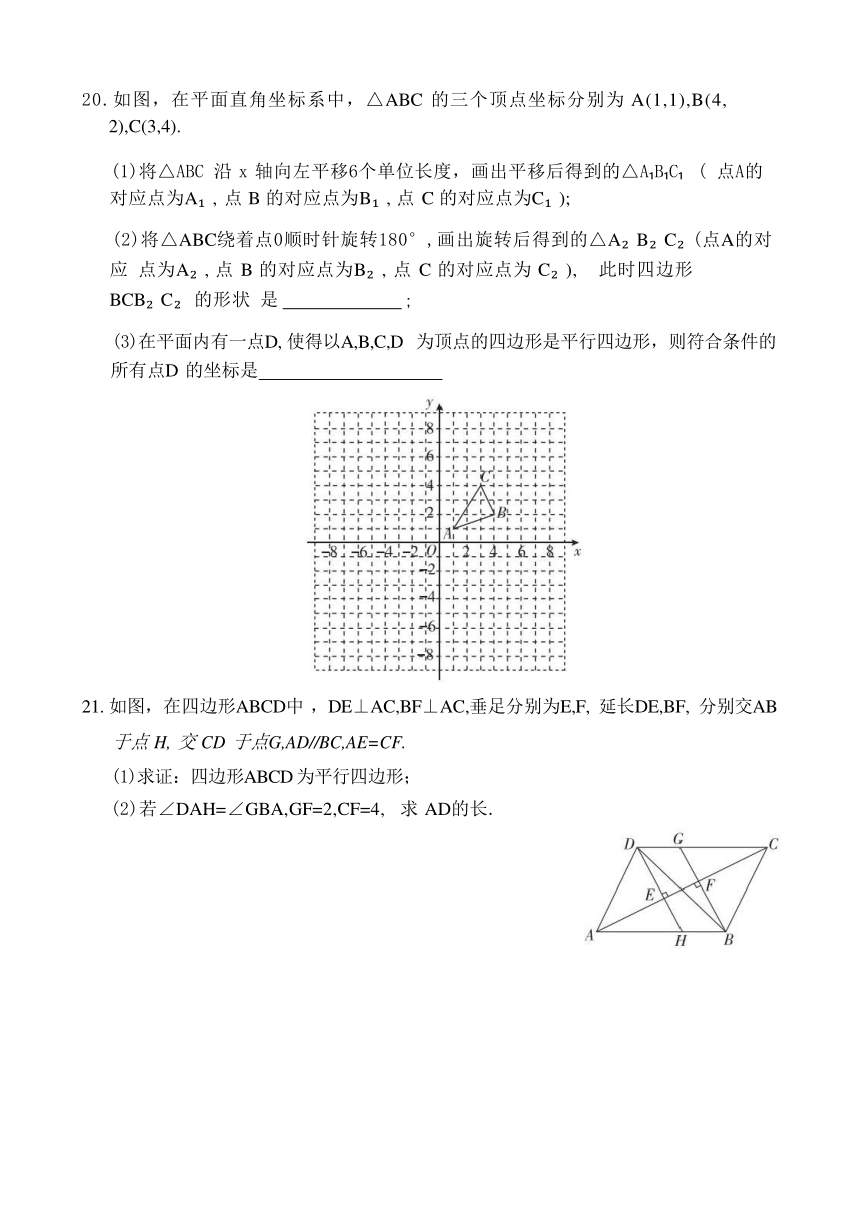
20.如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(1,1),B(4, 2),C(3,4).
(1)将△ABC 沿 x 轴向左平移6个单位长度,画出平移后得到的△A B C ( 点A的 对应点为A , 点 B 的对应点为B , 点 C 的对应点为C );
(2)将△ABC绕着点0顺时针旋转180°,画出旋转后得到的△A B C (点A的对应 点为A , 点 B 的对应点为B , 点 C 的对应点为 C ), 此时四边形 BCB C 的形状 是 ;
(3)在平面内有一点D, 使得以A,B,C,D 为顶点的四边形是平行四边形,则符合条件的 所有点D 的坐标是
21. 如图,在四边形ABCD中 ,DE⊥AC,BF⊥AC,垂足分别为E,F, 延长DE,BF, 分别交AB 于点 H, 交 CD 于点G,AD//BC,AE=CF.
(1)求证:四边形ABCD 为平行四边形;
(2)若∠DAH=∠GBA,GF=2,CF=4, 求 AD的长.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.某商场采购 A,B 两种品牌的卡通笔袋,已知每个 A 品牌笔袋的进价比每个 B 品 牌笔袋的进价多2元;用3000元购进 A 品牌笔袋的数量与用2400元购进B 品牌 笔袋的数量相同.
(1)求每个A 品牌笔袋和每个 B 品牌笔袋的进价.
(2)该商场计划用不超过7220元采购A,B 两种品牌的笔袋共800个,且其中B 品牌 笔袋的数量不超过400个,则该商场共有几种进货方式
23. 如图①,在Rt△ABC 中,∠A=90°,AB=AC, 点 D,E 分别在边AC,AB 上,AD=AE, 连接 DE,BD, 点 F,P,G 分别为DE,BD,BC 的中点,连接PF,PG.
(1)线段PF 与 PG 的数量关系是 ,位置关系是 ;
(
C
)(2)把△ADE 绕点A 顺时针旋转到图②的位置,连接 FG, 判断
△PFG 的形状,并说明理由;
(
D
)(3)若AD=3,AB=7,△ADE 绕点A 在平面内旋转,则当△PFG 的 面积取得最大值时 BD的长为
图①
期末质量检测卷(一)
1.A 2.B 3.D 4.C 5.B 6.A 7.B 8.A 9.A
10.C【 解析】如图,作 A(0,1)关于x 轴的对称点A'(0, -1),过点A'作A'E//x 轴且A'E=CD=2,则 E(2,-1),
连接 BE 交 x 轴于点D', 过点A′作A'C//D'E 交 x 轴 于
点 C',连接AC'. ∴四边形C'D'EA'为平行四边形 ∴D'E=A'C′=AC′,C'D′=A'E=CD. ∴AC′+BD′=D'E+BD′=BE. 当 CD移动至C'D'时, AC+BD=AC'+BD'=BE. 此时AC+BD 的值最小,最小值 A'
为 BE 的长.
∵BE==, ∴AC+BD 的最小值为.
11.ab(a+b)12.100°13.3014.1215.
16.解:方程两边都乘x-3, 得 2-x-1=x-3 解得x=2.
经检验,x=2 是原方程的根.
=x+3.
当x=2025时,原式=2025+3=2028.
18. (1)解:如图,DE 即为所求.
(2)证明:连接AD, 如图.
∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵DE 垂直平分AB,∴AD=BD.
∴∠DAB=∠B=30°.
∴∠CAD=∠BAC-∠DAB=120°-30°=90°.
∴CD=2AD. ∴CD=2BD.
19.解:(1)141515(答案不唯一)
(2)王老师当前年龄是34岁.理由如下:
x -x=x(x -1)=x(x+1)(x-1).
∵王老师手机的锁屏密码是6位数字353334,且(x+1)>x>(x-1),
∴x+1=35,x=34,x-1=33.
∴王老师当前年龄是34岁.
20.解:(1)如图,△A B C 即为所求.
(2)如图,△A B C 即为所求. 平行四边形
(3)(2,-1)或(0,3)或(6,5)
21. (1)证明:∵ DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°.
∵AD//BC, ∴∠DAE=∠BCF.
在△DAE和△BCF 中
∴△DAE≌△BCF(ASA).∴AD=CB.
又∵AD//BC,. 四边形ABCD 为平行四边形.
(2)解:∵四边形 ABCD为平行四边形,
∴∠DAH=∠BCG,AB//CD.
∴∠CGB=∠GBA.
∵∠DAH=∠GBA, ∴∠CGB=∠BCG.
∴BG=BC.
在 Rt△CFB 中,∵ BF=BG-GF=BC-2,CF=4,
∴BC =BF +CF =(BC-2) +4 .
解得 BC=5. ∴AD=BC=5.
22.解:(1)设每个B 品牌笔袋的进价为x 元,则每个 A 品 牌笔袋的进价为(x+2) 元 .
由题意,得.解得x=8.
经检验,x=8 是原分式方程的根.x+2=10.
答:每个A 品牌笔袋的进价是10元,每个 B 品牌笔袋 的进价是8元.
(2)设购买A品牌笔袋 m 个,则购买B 品牌笔袋(800-m)个.
由题意,得
解得400≤m≤410.
∵m 是整数,
∴m 可取400,401,402, …,410,即该商场共有11种进 货方式.
答:该商场共有11种进货方式.
23. 解:(1)PF=PG PF⊥PG
(2)△PFG 是等腰直角三角形.理由如下:
∵ 点F,P 分别是DE,BD 的中点,
∴PF//B
∵ 点P,G 分别是BD,BC的中点,
∴PG//CD,
由旋转,知∠CAD=∠BAE.
∵AC=AB,AD=AE,
∴△ACD≌△ABE(SAS).
∴∠ACD=∠ABE,CD=BE.
, ∴PF=PG. ∴△PFG 是等腰三角形.
∵PF//BE,∠DPF=∠DBE=∠ABE+∠ABD.
∵PG//CD, ∴∠BGP=∠DCG.
∴∠DPG=∠BGP+∠DBG=∠DCG+∠DBG.
∴∠FPG=∠DPF+∠DPG=∠ABE+∠ABD+∠DCG+ ∠DBG=∠ABE+∠DCG+∠ABD+∠DBG=∠ACD+∠DCG+∠ABC=∠ACB+∠ABC.
∵∠BAC=90°, ∴∠FPG=∠ACB+∠ABC=90°.
∴△PFG 是等腰直角三角形.
(3) [提示]由(2)知,△PFG是等腰直角三角形,
∴ 当GP 最大时,S△PFG 最大.
∴ 当CD最大时,GP最大. 当点D 在 CA 的延长线上 时 ,CD最大,如图.
此时 BD===
(满分:120分 时间:120分钟)
题号 一 二 三 四 五 总分
得分
一、选择题:本大题共10小题,每小题3分,共30分.在每小题给出的四个选项中,只有 一项是符合题目要求的.
1.下列图形是中心对称图形的是 ( )
A.平行四边形 B. 直角三角形
C. 等边三角形 D.正五边形
2.已知a>b,下列式子成立的是 ( )
A.ac >bc B
C.-a>-b D.a >b
3.多项式a +1 与下列单项式的和不可以因式分解的是 ( ) A.-2a B.2a C.-2 D.3
4.若分的值为0,则x 的值为 ( ) A.±3 B.3 C.-3 D.0
5.下列命题中,错误的是 ( )
A. 正八边形的每个外角都等于45°
B. 一组对边相等且另一组对边平行的四边形是平行四边形
C. 点 P(a,b) 关于原点对称的点的坐标为P'(-a,-b)
D. 角平分线上的点到这个角两边的距离相等
6.如图,在△ABC 中 ,AB 的垂直平分线交AB 于点D,交 BC 于点 E,连接AE. 若 BC=6, AC=5, 则△ACE 的周长为 ( ) A.11 B.12 C.16 D.17
第6题图
第7题图
7.如图,在平行四边形 ABCD 中,∠D=120°,AD=2 √3cm,AB=4 √3 cm,点 P 从点D 出发 以 √3 cm/s 的速度,沿D→C→B→A 在平行四边形的边上匀速运动至点A.设点P 的运 动时间为ts,△ADP 的面积为s cm ,下列图中表示s 与 t 之间函数关系的是( )
(
4s/cm
) (
12
) (
0
46
) (
12
√3
10
t/s
0
10
t/s
0
46
10
t/s
↑s/cm
12
√3
s/cm
5
)
A B C D
8.A,B 两地相距60 km, 一艘轮船从A 地顺流航行至B 地所用时间比从B 地逆流航行至 A 地所用时间少45 min,已知船在静水中航行的速度为20 km/h. 若设水流速度为 x km/h(x<20),则可列方程为 ( )
A.
C.
9.关于x 的不等式
B
D
恰好只有两个整数解,则 a 的取值范围是
( )
A.5≤a<6 B.5
图①
图②
第10题图 第12题图
二、填空题:本大题共5小题,每小题3分,共15分.
11.因式分解:a b+ab =
12.“岭南四大名园”之一的佛山“梁园”里不仅有秀水、奇石、名帖,还有随处可见的古典 窗棂(如图①所示),这也是岭南建筑艺术之一.图②是这种窗棂中的部分图案,其中
∠1,∠2,∠3,∠4是五边形ABCDE 的4个外角.若∠1+∠2+∠3+∠4=280°,则∠D 的度数是
13. 如图,已知△ABC的周长是15,0B,OC 分别平分∠ABC 和∠ACB,OD⊥BC于点D,且 OD=4, 则△ABC的面积是
第13题图
第15题图
14.小明4岁那年父亲种下一棵山毛榉和一棵枫树.当时山毛榉高3m, 枫树高1.8 m, 现 在枫树已经比山毛榉高了.在此期间,山毛榉的平均生长速度是每年长高0.15m, 枫 树的平均生长速度是每年长高0.3 m. 请问小明现在的年龄应该超过 岁.
15.如图,在平行四边形ABCD中 ,AB=4,沿对角线AC 翻折,点B 的对应点为B',B'C 与 AD交于点E, 此时△CDE 恰为等边三角形,则重叠部分(即图中阴影部分)的面积 为
三、解答题(一):本大题共3小题,每小题7分,共21分.
16.解方程
17.先化简再求值:,且x=2025.
18.如图,在△ABC 中 ,AB=AC,∠BAC=120°.
(1)尺规作图:作线段AB 的垂直平分线 DE, 交AB 于点E,交 BC 于点D (保留作图痕 迹,不写作法);
(2)求证:CD=2BD.
四、解答题(二):本大题共3小题,每小题9分,共27分.
19.阅读与思考:
在现今信息化时代,智能手机几乎人手必备,应用到了生活的各个领域,锁屏密码为 保护我们个人隐私起到了不可或缺的作用,而诸如“1234”、生日等简单密码又容易被 破解,因此利用简单方法产生一组容易记忆的密码就很有必要了.有一种用“因式分 解”法产生的密码,方便记忆,其原理是:将一个多项式分解因式,如多项式:x -1 因 式分解的结果为(x-1)(x+1) 或(x+1)(x-1), 取个人年龄作为x 的值,当x=13时, x-1=12,x+1=14, 此时可以得到数字密码1214或1412.
(1)根据上述方法,若多项式为x +2x+1, 请你结合个人年龄设置一个锁屏密码,当 x=_ 时,锁屏密码为 ;
(2)若王老师选取的多项式为x -x,已知王老师手机的锁屏密码是6位数字353334, 请尝试分析王老师当前年龄是多少岁,并说明理由.
20.如图,在平面直角坐标系中,△ABC 的三个顶点坐标分别为 A(1,1),B(4, 2),C(3,4).
(1)将△ABC 沿 x 轴向左平移6个单位长度,画出平移后得到的△A B C ( 点A的 对应点为A , 点 B 的对应点为B , 点 C 的对应点为C );
(2)将△ABC绕着点0顺时针旋转180°,画出旋转后得到的△A B C (点A的对应 点为A , 点 B 的对应点为B , 点 C 的对应点为 C ), 此时四边形 BCB C 的形状 是 ;
(3)在平面内有一点D, 使得以A,B,C,D 为顶点的四边形是平行四边形,则符合条件的 所有点D 的坐标是
21. 如图,在四边形ABCD中 ,DE⊥AC,BF⊥AC,垂足分别为E,F, 延长DE,BF, 分别交AB 于点 H, 交 CD 于点G,AD//BC,AE=CF.
(1)求证:四边形ABCD 为平行四边形;
(2)若∠DAH=∠GBA,GF=2,CF=4, 求 AD的长.
五、解答题(三):本大题共2小题,第22题13分,第23题14分,共27分.
22.某商场采购 A,B 两种品牌的卡通笔袋,已知每个 A 品牌笔袋的进价比每个 B 品 牌笔袋的进价多2元;用3000元购进 A 品牌笔袋的数量与用2400元购进B 品牌 笔袋的数量相同.
(1)求每个A 品牌笔袋和每个 B 品牌笔袋的进价.
(2)该商场计划用不超过7220元采购A,B 两种品牌的笔袋共800个,且其中B 品牌 笔袋的数量不超过400个,则该商场共有几种进货方式
23. 如图①,在Rt△ABC 中,∠A=90°,AB=AC, 点 D,E 分别在边AC,AB 上,AD=AE, 连接 DE,BD, 点 F,P,G 分别为DE,BD,BC 的中点,连接PF,PG.
(1)线段PF 与 PG 的数量关系是 ,位置关系是 ;
(
C
)(2)把△ADE 绕点A 顺时针旋转到图②的位置,连接 FG, 判断
△PFG 的形状,并说明理由;
(
D
)(3)若AD=3,AB=7,△ADE 绕点A 在平面内旋转,则当△PFG 的 面积取得最大值时 BD的长为
图①
期末质量检测卷(一)
1.A 2.B 3.D 4.C 5.B 6.A 7.B 8.A 9.A
10.C【 解析】如图,作 A(0,1)关于x 轴的对称点A'(0, -1),过点A'作A'E//x 轴且A'E=CD=2,则 E(2,-1),
连接 BE 交 x 轴于点D', 过点A′作A'C//D'E 交 x 轴 于
点 C',连接AC'. ∴四边形C'D'EA'为平行四边形 ∴D'E=A'C′=AC′,C'D′=A'E=CD. ∴AC′+BD′=D'E+BD′=BE. 当 CD移动至C'D'时, AC+BD=AC'+BD'=BE. 此时AC+BD 的值最小,最小值 A'
为 BE 的长.
∵BE==, ∴AC+BD 的最小值为.
11.ab(a+b)12.100°13.3014.1215.
16.解:方程两边都乘x-3, 得 2-x-1=x-3 解得x=2.
经检验,x=2 是原方程的根.
=x+3.
当x=2025时,原式=2025+3=2028.
18. (1)解:如图,DE 即为所求.
(2)证明:连接AD, 如图.
∵AB=AC,∠BAC=120°, ∴∠B=∠C=30°.
∵DE 垂直平分AB,∴AD=BD.
∴∠DAB=∠B=30°.
∴∠CAD=∠BAC-∠DAB=120°-30°=90°.
∴CD=2AD. ∴CD=2BD.
19.解:(1)141515(答案不唯一)
(2)王老师当前年龄是34岁.理由如下:
x -x=x(x -1)=x(x+1)(x-1).
∵王老师手机的锁屏密码是6位数字353334,且(x+1)>x>(x-1),
∴x+1=35,x=34,x-1=33.
∴王老师当前年龄是34岁.
20.解:(1)如图,△A B C 即为所求.
(2)如图,△A B C 即为所求. 平行四边形
(3)(2,-1)或(0,3)或(6,5)
21. (1)证明:∵ DE⊥AC,BF⊥AC,
∴∠DEA=∠BFC=90°.
∵AD//BC, ∴∠DAE=∠BCF.
在△DAE和△BCF 中
∴△DAE≌△BCF(ASA).∴AD=CB.
又∵AD//BC,. 四边形ABCD 为平行四边形.
(2)解:∵四边形 ABCD为平行四边形,
∴∠DAH=∠BCG,AB//CD.
∴∠CGB=∠GBA.
∵∠DAH=∠GBA, ∴∠CGB=∠BCG.
∴BG=BC.
在 Rt△CFB 中,∵ BF=BG-GF=BC-2,CF=4,
∴BC =BF +CF =(BC-2) +4 .
解得 BC=5. ∴AD=BC=5.
22.解:(1)设每个B 品牌笔袋的进价为x 元,则每个 A 品 牌笔袋的进价为(x+2) 元 .
由题意,得.解得x=8.
经检验,x=8 是原分式方程的根.x+2=10.
答:每个A 品牌笔袋的进价是10元,每个 B 品牌笔袋 的进价是8元.
(2)设购买A品牌笔袋 m 个,则购买B 品牌笔袋(800-m)个.
由题意,得
解得400≤m≤410.
∵m 是整数,
∴m 可取400,401,402, …,410,即该商场共有11种进 货方式.
答:该商场共有11种进货方式.
23. 解:(1)PF=PG PF⊥PG
(2)△PFG 是等腰直角三角形.理由如下:
∵ 点F,P 分别是DE,BD 的中点,
∴PF//B
∵ 点P,G 分别是BD,BC的中点,
∴PG//CD,
由旋转,知∠CAD=∠BAE.
∵AC=AB,AD=AE,
∴△ACD≌△ABE(SAS).
∴∠ACD=∠ABE,CD=BE.
, ∴PF=PG. ∴△PFG 是等腰三角形.
∵PF//BE,∠DPF=∠DBE=∠ABE+∠ABD.
∵PG//CD, ∴∠BGP=∠DCG.
∴∠DPG=∠BGP+∠DBG=∠DCG+∠DBG.
∴∠FPG=∠DPF+∠DPG=∠ABE+∠ABD+∠DCG+ ∠DBG=∠ABE+∠DCG+∠ABD+∠DBG=∠ACD+∠DCG+∠ABC=∠ACB+∠ABC.
∵∠BAC=90°, ∴∠FPG=∠ACB+∠ABC=90°.
∴△PFG 是等腰直角三角形.
(3) [提示]由(2)知,△PFG是等腰直角三角形,
∴ 当GP 最大时,S△PFG 最大.
∴ 当CD最大时,GP最大. 当点D 在 CA 的延长线上 时 ,CD最大,如图.
此时 BD===
同课章节目录
