冀教版(2024)数学七年级上册 1.3 绝对值与相反数 课件(共25张PPT)
文档属性
| 名称 | 冀教版(2024)数学七年级上册 1.3 绝对值与相反数 课件(共25张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 15.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 20:44:36 | ||
图片预览







文档简介
(共25张PPT)
[图片]
1.3 绝对值与相反数
冀教版(2024)
七年级上册
学习目标
理解绝对值的概念及其几何意义.(重点)
01
借助数轴掌握相反数的意义,了解数轴上相反数关于原点对称.(重点)
02
会求有理数的相反数与绝对值.(重点)
03
明晰绝对值的非负性,并能进行具体应用.(难点)
04
在数轴上有这样一些成对出现的点,它们到原点的距离相等,表示的数的符号却相反.为了描述这类数的特征,我们需要学习绝对值和相反数的知识.
新课导学
小明家位于学校正东方向1500m处,小亮家位于学校正西方向1500m处.请以学校为原点画一条数轴,并把小明家和小亮家的位置在数轴上表示出来.你有什么发现?
0
1500
小明家
小亮家
发现:小明家对应的数和小亮家对应的数,互为相反数;且它们在数轴上的点,关于原点对称.
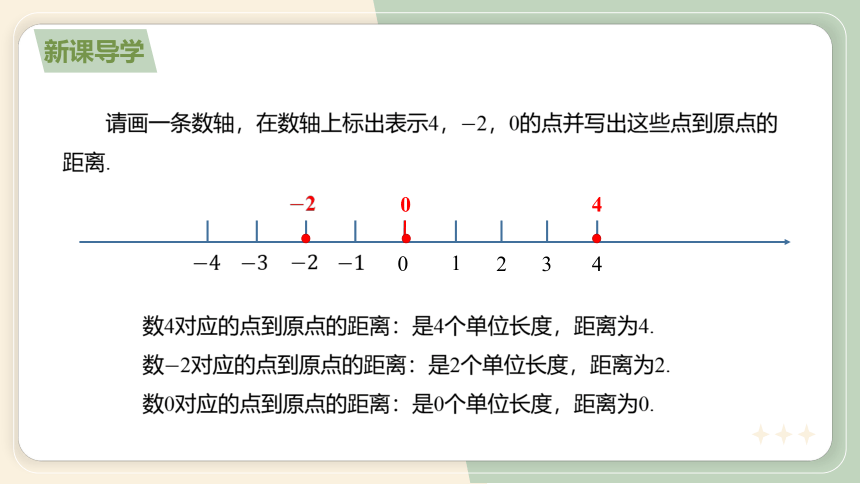
请画一条数轴,在数轴上标出表示4,2,0的点并写出这些点到原点的距离.
新课导学
0
0
1
2
3
4
4
2
数4对应的点到原点的距离:是4个单位长度,距离为4.
数2对应的点到原点的距离:是2个单位长度,距离为2.
数0对应的点到原点的距离:是0个单位长度,距离为0.
绝对值
新知探索
绝对值:在数轴上,表示一个数的点到原点的距离叫作这个数的绝对值.有理数a的绝对值表示为|a|,读作“a的绝对值”.
在数轴上,表示4的点到原点的距离是4,所以4的绝对值是4,记作|4| =4;表示2的点到原点的距离是2,所以2的绝对值是2,记作|2| =2;表示0的点到原点的距离是0,所以0的绝对值是0,记作|0|=0.
新知探索
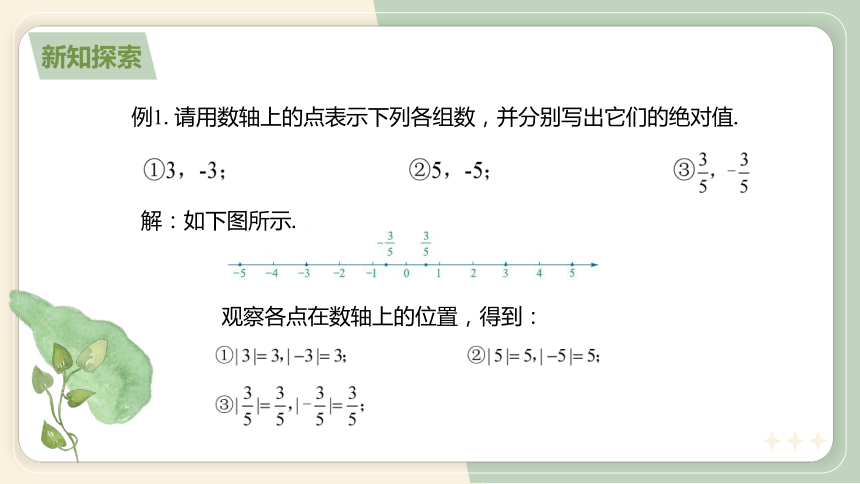
例1. 请用数轴上的点表示下列各组数,并分别写出它们的绝对值.
解:如下图所示.
观察各点在数轴上的位置,得到:
观察例1中的三组数在数轴上的位置和绝对值的大小,思考这三组数的共同特点是什么,并与同学交流.
符号相反:每组数包含一个正数和一个负数(如3与3).
绝对值相等:每组数的两个数到原点的距离相同.
关于原点对称:在数轴上,每组数对应的点分别位于原点两侧,且到原点的距离相等(几何上关于原点对称)...
新知探索
相反数
新知探索
相反数:像3和3,5和5,和等这样符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.规定0的相反数为0.
表示一个数的相反数时,可以在这个数的前面添加一个“”.因此,有理数a的相反数可以表示为a.
例如,4的相反数可以表示为(4).
因为4的相反数是4,所以(4)=4.
例2:请化简下列各数:
新知探索
一个正数的绝对值与这个数有什么关系?一个负数的绝对值与这个数有什么关系?0的绝对值是多少呢?
新课导学
由绝对值的意义,可以得知:
一个正数的绝对值是它本身,
一个负数的绝对值是它的相反数,
0的绝对值是0.
例3.求下列各数的绝对值:
新知探索
互为相反数的两个数的绝对值相等.
练习
1.求下列各数的绝对值:
6
3.下列各判断是否正确?为什么?
(1)有理数的绝对值一定是正数.
(2)如果两个数的绝对值相等,那么这两个数也相等.
(3)绝对值等于它本身的数一定不是负数.
(4)绝对值等于1的数有两个.
练习
练习
(1)错误.有理数包含0,0的绝对值是0,不是正数.
(2)错误.绝对值相等的两个数,可能相等,也可能互为相反数.
(3)正确.正数的绝对值是它本身,0的绝对值是0(也等于本身 ),而负数的绝对值是它的相反数(与本身不相等).
(4)正确.根据绝对值定义,|1|=1,|1|=1,所以绝对值等于1的数是1和1,共两个.
新知探索
1.任何有理数都有绝对值,且只有一个.
3.互为相反数的两个数的绝对值相等.
2.相反数是成对出现的,不能单独存在.
5.在数轴上,表示互为相反数的两个点位于原点的两侧,且到原点的距离相等.
绝对值与相反数:
4.绝对值相等的两个数相等或互为相反数.
课堂巩固
A
课堂巩固
D
课堂巩固
B
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
3,4,3,4
新知探索
1、绝对值的概念.
2、相反数的概念.
3、绝对值与相反数的实际应用.
课堂总结
谢谢观看
[图片]
1.3 绝对值与相反数
冀教版(2024)
七年级上册
学习目标
理解绝对值的概念及其几何意义.(重点)
01
借助数轴掌握相反数的意义,了解数轴上相反数关于原点对称.(重点)
02
会求有理数的相反数与绝对值.(重点)
03
明晰绝对值的非负性,并能进行具体应用.(难点)
04
在数轴上有这样一些成对出现的点,它们到原点的距离相等,表示的数的符号却相反.为了描述这类数的特征,我们需要学习绝对值和相反数的知识.
新课导学
小明家位于学校正东方向1500m处,小亮家位于学校正西方向1500m处.请以学校为原点画一条数轴,并把小明家和小亮家的位置在数轴上表示出来.你有什么发现?
0
1500
小明家
小亮家
发现:小明家对应的数和小亮家对应的数,互为相反数;且它们在数轴上的点,关于原点对称.
请画一条数轴,在数轴上标出表示4,2,0的点并写出这些点到原点的距离.
新课导学
0
0
1
2
3
4
4
2
数4对应的点到原点的距离:是4个单位长度,距离为4.
数2对应的点到原点的距离:是2个单位长度,距离为2.
数0对应的点到原点的距离:是0个单位长度,距离为0.
绝对值
新知探索
绝对值:在数轴上,表示一个数的点到原点的距离叫作这个数的绝对值.有理数a的绝对值表示为|a|,读作“a的绝对值”.
在数轴上,表示4的点到原点的距离是4,所以4的绝对值是4,记作|4| =4;表示2的点到原点的距离是2,所以2的绝对值是2,记作|2| =2;表示0的点到原点的距离是0,所以0的绝对值是0,记作|0|=0.
新知探索
例1. 请用数轴上的点表示下列各组数,并分别写出它们的绝对值.
解:如下图所示.
观察各点在数轴上的位置,得到:
观察例1中的三组数在数轴上的位置和绝对值的大小,思考这三组数的共同特点是什么,并与同学交流.
符号相反:每组数包含一个正数和一个负数(如3与3).
绝对值相等:每组数的两个数到原点的距离相同.
关于原点对称:在数轴上,每组数对应的点分别位于原点两侧,且到原点的距离相等(几何上关于原点对称)...
新知探索
相反数
新知探索
相反数:像3和3,5和5,和等这样符号不同、绝对值相等的两个数,我们称其中一个数是另一个数的相反数,也称这两个数互为相反数.规定0的相反数为0.
表示一个数的相反数时,可以在这个数的前面添加一个“”.因此,有理数a的相反数可以表示为a.
例如,4的相反数可以表示为(4).
因为4的相反数是4,所以(4)=4.
例2:请化简下列各数:
新知探索
一个正数的绝对值与这个数有什么关系?一个负数的绝对值与这个数有什么关系?0的绝对值是多少呢?
新课导学
由绝对值的意义,可以得知:
一个正数的绝对值是它本身,
一个负数的绝对值是它的相反数,
0的绝对值是0.
例3.求下列各数的绝对值:
新知探索
互为相反数的两个数的绝对值相等.
练习
1.求下列各数的绝对值:
6
3.下列各判断是否正确?为什么?
(1)有理数的绝对值一定是正数.
(2)如果两个数的绝对值相等,那么这两个数也相等.
(3)绝对值等于它本身的数一定不是负数.
(4)绝对值等于1的数有两个.
练习
练习
(1)错误.有理数包含0,0的绝对值是0,不是正数.
(2)错误.绝对值相等的两个数,可能相等,也可能互为相反数.
(3)正确.正数的绝对值是它本身,0的绝对值是0(也等于本身 ),而负数的绝对值是它的相反数(与本身不相等).
(4)正确.根据绝对值定义,|1|=1,|1|=1,所以绝对值等于1的数是1和1,共两个.
新知探索
1.任何有理数都有绝对值,且只有一个.
3.互为相反数的两个数的绝对值相等.
2.相反数是成对出现的,不能单独存在.
5.在数轴上,表示互为相反数的两个点位于原点的两侧,且到原点的距离相等.
绝对值与相反数:
4.绝对值相等的两个数相等或互为相反数.
课堂巩固
A
课堂巩固
D
课堂巩固
B
课堂巩固
C
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
3,4,3,4
新知探索
1、绝对值的概念.
2、相反数的概念.
3、绝对值与相反数的实际应用.
课堂总结
谢谢观看
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
