冀教版(2024)数学七年级上册 1.1 正数和负数 课件(共28张PPT)
文档属性
| 名称 | 冀教版(2024)数学七年级上册 1.1 正数和负数 课件(共28张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 16.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 20:46:25 | ||
图片预览








文档简介
(共28张PPT)
[图片]
1.1 正数和负数
冀教版(2024)
七年级上册
学习目标
能够准确识别正数与负数,理解其具体意义.(重点)
01
依据实际情境,正确使用正数和负数表示具有相反意义的量.(重点)
02
理解 0 的特殊性,知道它的具体用法.(难点)
03
在小学阶段,我们学习了自然数、小数、分数以及它们的四则运算和简单应用,在现实生活中,我们还经常遇到收入和支出,零上气温和零下气温等具有相反意义的量.为了表示这些量,需要引入负数,数的范围又一次扩大了.
新课导学
下图是某地7天最低气温的趋势预报,你能按照由低到高的顺序把这七天的最低气温排列出来吗?
,,,0,1,2,4
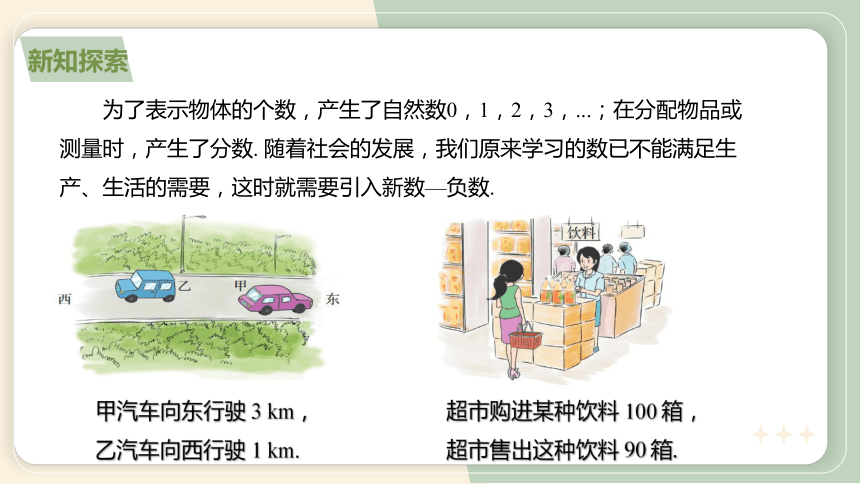
为了表示物体的个数,产生了自然数0,1,2,3,...;在分配物品或测量时,产生了分数. 随着社会的发展,我们原来学习的数已不能满足生产、生活的需要,这时就需要引入新数—负数.
甲汽车向东行驶 3 km,
乙汽车向西行驶 1 km.
超市购进某种饮料 100 箱,
超市售出这种饮料 90 箱.
新知探索
观察上图中的两幅图片,请根据图片下方的说明,思考以下问题:
观察与思考
(1)向东和向西,购进和售出所表达的意义具有怎样的关系呢?
(2)如果仅说3km,1km和100箱,90箱,能完整地表达出它们的意义吗?为什么?
向东和向西是一对具有相反意义的量;
购进和售出是一对具有相反意义的量.
不能.
缺少方向性和增减趋势.
观察下图,请回答下面的问题:
新知探索
(1)在左图中,21,188,100,80的含义分别是什么?
(2)在右图中,“2”与“2”这两个按键所代表的含义有什么不同?
21,100表示支出金额;188,80表示收入金额.
2是负数,表示地下二层;2是正数,表示地上二层.
一般地,对于具有相反意义的量,我们可以把其中一种意义的量规定为正的,并在表示这个量的数的前面加上“”(读作“正”)来表示;把与它意义相反的量规定为负的,并在表示这个量的数的前面加上“”(读作“负”)来表示.
例如:规定收入为正、支出为负,则收入188元可表示为元,读作“正188元”;支出21元可表示为21元,读作“负21元”.
具有相反意义的量
新知探索
新知探索
1、请仿照上述表示相反意义的量的方法,完成下表
km
水位下降50cm
2、用带“”或“”的数表示下列具有相反意义的量:
(1)如果超市购进某种饮料100箱记作+100箱,那么超市售出这种饮料90箱可记作____箱.
(2)如果规定高于海平面记作正,那么,珠穆朗玛峰高于海平面8848.86m 可记作_________m,吐鲁番盆地最低点低于海平面154.31m 可记作________m.
(3)如果规定收入记作正,那么,小亮家的年收入126800元可记作________元,
“元”表示小亮家______(填“收入”或“支出”)了77800元.
支出
1.下面哪对量是具有相反意义的量
(1)在知识竞赛中,得20分和扣10分.
(2)一座水库蓄水量增加10000 m3 和减少12000 m3.
(3)一辆公共汽车在一个停车站下去10名乘客和上来8名乘客.
(4)长方形的周长是24 cm 和面积是27 cm2.
练习
(1)(2)(3)是具有相反意义的量.
(4)周长和面积不具有相反意义.
(1)如果飞机上升200 m 记作200m,那么飞机下降300 m 可记作_____m.
(2)如果规定铅球的质量高于标准质量的部分为正,低于标准质量的部分为负,那么,甲铅球高于标准质量3g可记作___g,乙铅球低于标准质量2g可记作___g.
(3)如果规定木材公司购进木材为正,售出木材为负,那么,该公司购进木材2000m3 可记作______m3,售出木材1500m3 可记作______m3.
2.填空:
练习
正数与负数
新知探索
负数:我们用带“”和“”的数统一地表示出具有相反意义的量,从而得到了,,等这样形式的数,它们都是在已学过的数(0除外)的前面加上“”得到的,这样的数叫作负数;
正数:,,等这样形式的数,都是在已学过的数(0 除外)的前面加上“”得到的,这样的数叫作正数.
新知探索
1.通常情况下,正数前的正号可以省略.如1.8可以写成1.8等等.
2.负号不可以省略.
3.0 既不是正数,也不是负数.
4.判断一个数是正数还是负数时,不能简单地理解为带“”号的数就是正数,带“”号的就是负数.
应注意的问题:
新知探索
某水库一监测点将水深为5m 处的水面设定为警戒水位,规定超过警戒水位的部分记为正,低于警戒水位的部分记为负.
(1)“”表示什么意义 此时水库监测点的实际水深是多少米
(2)“0m”表示_______,此时水库监测点的实际水深是多少米
(3)“”表示的意义是什么 此时水库监测点的实际水深是多少米
(1)表示超过警戒水位1m;此时实际水深是6m.
(2)0m表示位于警戒水位;此时实际水深是5m.
(3)表示低于警戒水位2m;此时实际水深是3m.
新知探索
根据有理数的意义,我们知道有理数可做如下分类:
有理数
整数
分数
正整数、0和负整数统称为整数,正分数和负分数统称为分数,整数和分数统称为有理数.
0是正数和负数的分界.
你能进一步将整数和分数分类吗 有理数还有其他分类方法吗 请把你的想法与同学交流一下.
整数可分为正整数、0、负整数;分数可分为正分数和负分数.
有理数还可分为正有理数、0、负有理数.
请把下列各数分别填入相应的圈内:
新知探索
练习
新知探索
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
课堂总结
新知探索
1、了解相反意义的量(如收入与支出、上升与下降)2、区分正数与负数,并能实际应用.
3、熟悉 0 的实际意义.
谢谢观看
[图片]
1.1 正数和负数
冀教版(2024)
七年级上册
学习目标
能够准确识别正数与负数,理解其具体意义.(重点)
01
依据实际情境,正确使用正数和负数表示具有相反意义的量.(重点)
02
理解 0 的特殊性,知道它的具体用法.(难点)
03
在小学阶段,我们学习了自然数、小数、分数以及它们的四则运算和简单应用,在现实生活中,我们还经常遇到收入和支出,零上气温和零下气温等具有相反意义的量.为了表示这些量,需要引入负数,数的范围又一次扩大了.
新课导学
下图是某地7天最低气温的趋势预报,你能按照由低到高的顺序把这七天的最低气温排列出来吗?
,,,0,1,2,4
为了表示物体的个数,产生了自然数0,1,2,3,...;在分配物品或测量时,产生了分数. 随着社会的发展,我们原来学习的数已不能满足生产、生活的需要,这时就需要引入新数—负数.
甲汽车向东行驶 3 km,
乙汽车向西行驶 1 km.
超市购进某种饮料 100 箱,
超市售出这种饮料 90 箱.
新知探索
观察上图中的两幅图片,请根据图片下方的说明,思考以下问题:
观察与思考
(1)向东和向西,购进和售出所表达的意义具有怎样的关系呢?
(2)如果仅说3km,1km和100箱,90箱,能完整地表达出它们的意义吗?为什么?
向东和向西是一对具有相反意义的量;
购进和售出是一对具有相反意义的量.
不能.
缺少方向性和增减趋势.
观察下图,请回答下面的问题:
新知探索
(1)在左图中,21,188,100,80的含义分别是什么?
(2)在右图中,“2”与“2”这两个按键所代表的含义有什么不同?
21,100表示支出金额;188,80表示收入金额.
2是负数,表示地下二层;2是正数,表示地上二层.
一般地,对于具有相反意义的量,我们可以把其中一种意义的量规定为正的,并在表示这个量的数的前面加上“”(读作“正”)来表示;把与它意义相反的量规定为负的,并在表示这个量的数的前面加上“”(读作“负”)来表示.
例如:规定收入为正、支出为负,则收入188元可表示为元,读作“正188元”;支出21元可表示为21元,读作“负21元”.
具有相反意义的量
新知探索
新知探索
1、请仿照上述表示相反意义的量的方法,完成下表
km
水位下降50cm
2、用带“”或“”的数表示下列具有相反意义的量:
(1)如果超市购进某种饮料100箱记作+100箱,那么超市售出这种饮料90箱可记作____箱.
(2)如果规定高于海平面记作正,那么,珠穆朗玛峰高于海平面8848.86m 可记作_________m,吐鲁番盆地最低点低于海平面154.31m 可记作________m.
(3)如果规定收入记作正,那么,小亮家的年收入126800元可记作________元,
“元”表示小亮家______(填“收入”或“支出”)了77800元.
支出
1.下面哪对量是具有相反意义的量
(1)在知识竞赛中,得20分和扣10分.
(2)一座水库蓄水量增加10000 m3 和减少12000 m3.
(3)一辆公共汽车在一个停车站下去10名乘客和上来8名乘客.
(4)长方形的周长是24 cm 和面积是27 cm2.
练习
(1)(2)(3)是具有相反意义的量.
(4)周长和面积不具有相反意义.
(1)如果飞机上升200 m 记作200m,那么飞机下降300 m 可记作_____m.
(2)如果规定铅球的质量高于标准质量的部分为正,低于标准质量的部分为负,那么,甲铅球高于标准质量3g可记作___g,乙铅球低于标准质量2g可记作___g.
(3)如果规定木材公司购进木材为正,售出木材为负,那么,该公司购进木材2000m3 可记作______m3,售出木材1500m3 可记作______m3.
2.填空:
练习
正数与负数
新知探索
负数:我们用带“”和“”的数统一地表示出具有相反意义的量,从而得到了,,等这样形式的数,它们都是在已学过的数(0除外)的前面加上“”得到的,这样的数叫作负数;
正数:,,等这样形式的数,都是在已学过的数(0 除外)的前面加上“”得到的,这样的数叫作正数.
新知探索
1.通常情况下,正数前的正号可以省略.如1.8可以写成1.8等等.
2.负号不可以省略.
3.0 既不是正数,也不是负数.
4.判断一个数是正数还是负数时,不能简单地理解为带“”号的数就是正数,带“”号的就是负数.
应注意的问题:
新知探索
某水库一监测点将水深为5m 处的水面设定为警戒水位,规定超过警戒水位的部分记为正,低于警戒水位的部分记为负.
(1)“”表示什么意义 此时水库监测点的实际水深是多少米
(2)“0m”表示_______,此时水库监测点的实际水深是多少米
(3)“”表示的意义是什么 此时水库监测点的实际水深是多少米
(1)表示超过警戒水位1m;此时实际水深是6m.
(2)0m表示位于警戒水位;此时实际水深是5m.
(3)表示低于警戒水位2m;此时实际水深是3m.
新知探索
根据有理数的意义,我们知道有理数可做如下分类:
有理数
整数
分数
正整数、0和负整数统称为整数,正分数和负分数统称为分数,整数和分数统称为有理数.
0是正数和负数的分界.
你能进一步将整数和分数分类吗 有理数还有其他分类方法吗 请把你的想法与同学交流一下.
整数可分为正整数、0、负整数;分数可分为正分数和负分数.
有理数还可分为正有理数、0、负有理数.
请把下列各数分别填入相应的圈内:
新知探索
练习
新知探索
课堂巩固
C
课堂巩固
课堂巩固
D
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
B
课堂巩固
课堂巩固
课堂总结
新知探索
1、了解相反意义的量(如收入与支出、上升与下降)2、区分正数与负数,并能实际应用.
3、熟悉 0 的实际意义.
谢谢观看
同课章节目录
- 第一章 有理数
- 1.1 正数和负数
- 1.2 数轴
- 1.3 绝对值与相反数
- 1.4 有理数的大小
- 1.5 有理数的加法
- 1.6 有理数的减法
- 1.7 有理数的加减混合运算
- 1.8 有理数的乘法
- 1.9 有理数的除法
- 1.10 有理数的乘方
- 1.11 有理数的混合运算
- 1.12 计算器的使用
- 第二章 几何图形的初步认识
- 2.1 从生活中认识几何图形
- 2.2 点和线
- 2.3 线段长短的比较
- 2.4 线段的和与差
- 2.5 角以及角的度量
- 2.6 角的大小
- 2.7 角的和与差
- 2.8 平面图形的旋转
- 第三章 代数式
- 3.1 用字母表示数
- 3.2 代数式
- 3.3 代数式的值
- 第四章 整式的加减
- 4.1 整式
- 4.2 合并同类项
- 4.3 去括号
- 4.4 整式的加减
- 第五章 一元一次方程
- 5.1一元一次方程
- 5.2 等式的基本性质
- 5.3 解一元一次方程
- 5.4 一元一次方程的应用
