沪科版数学八年级下册 第19章 四边形 单元测试(含答案)
文档属性
| 名称 | 沪科版数学八年级下册 第19章 四边形 单元测试(含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 120.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 20:49:07 | ||
图片预览




文档简介
沪科版八年级下 第19章 四边形 单元测试
一.选择题(共12小题)
1.(2025春 青山区期中)如图,在 ABCD中,AB=AC,∠D=40°,则∠ACB的度数为( )
A.55° B.50° C.45° D.40°
2.(2025春 肥西县期中)如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作AE⊥BD于点E,若DE=2BE,,则BC=( )
A. B.5 C. D.
3.(2025 蓝田县二模)如图,在 ABCD中,对角线AC交BD于O,已知AB=10,AC=12,BD=16,那么O到BC的距离为( )
A.4 B.4.8 C.5 D.6
4.如图,在 ABCD中,∠ABC的角平分线交AD于点E,若AB=3,ED=2,则BC的长度为( )
A.3 B.4 C.5 D.6
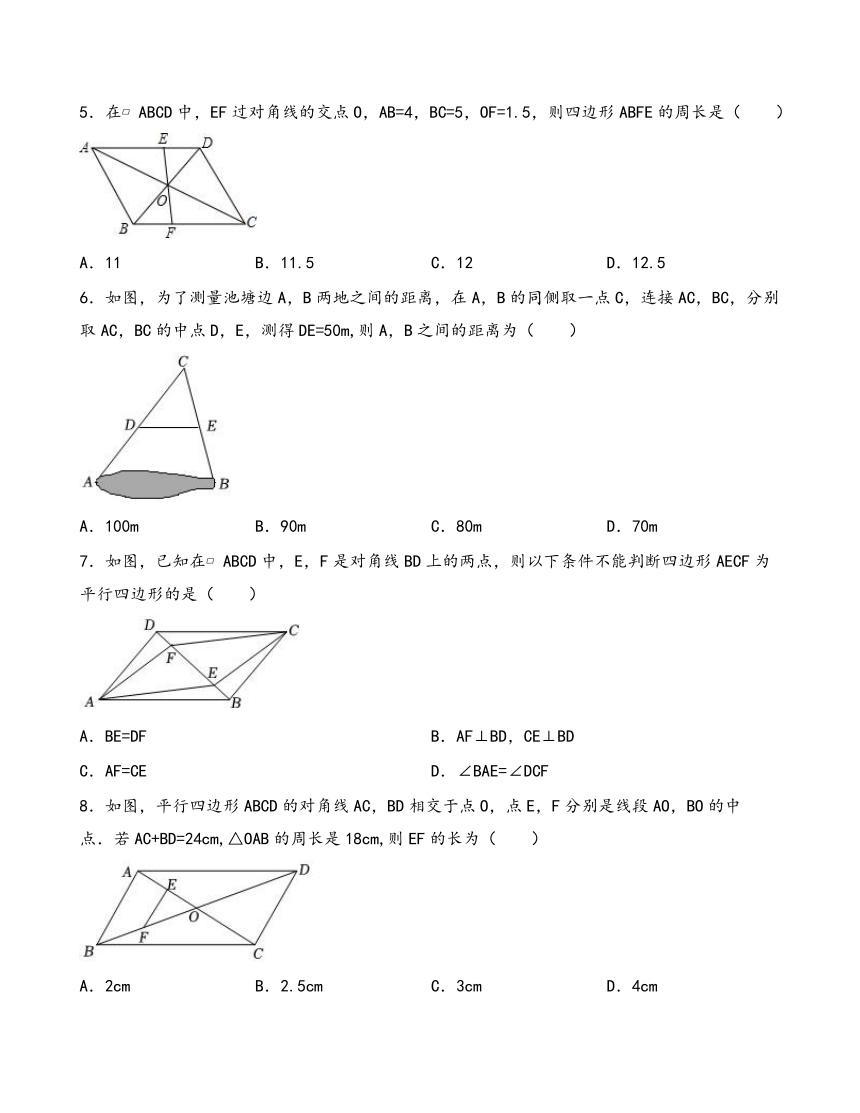
5.在 ABCD中,EF过对角线的交点O,AB=4,BC=5,OF=1.5,则四边形ABFE的周长是( )
A.11 B.11.5 C.12 D.12.5
6.如图,为了测量池塘边A,B两地之间的距离,在A,B的同侧取一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50m,则A,B之间的距离为( )
A.100m B.90m C.80m D.70m
7.如图,已知在 ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
A.BE=DF B.AF⊥BD,CE⊥BD
C.AF=CE D.∠BAE=∠DCF
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.2cm B.2.5cm C.3cm D.4cm
9.如图,已知在矩形ABCD中,AE⊥BD于点E,∠ABD=36°,则∠CAE的度数是( )
A.36° B.54° C.18° D.以上都不对
10.如图,在△ABC中,AB=AC=8,AN平分∠BAC交BC于点N,点M在BA上,且AM=3,连接CM,P为CM的中点,连接PN,则PN的长为( )
A.2.4 B.2 C.1.5 D.2.5
11.如图,在正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,EF.点P是EF的中点,连接CP,DP,若AE=AF,∠CPD=α,则∠CEF的度数为( )
A.α-45° B.135°-α C.2α-180° D.180°-α
12.(2025春 温州期中)如图,在 ABCD中,AC,BD相交于点O,过点A作AE⊥BC,AF⊥BD,AE=2AF,.记BE长为x,BO长为y(x≠0,y≠0).当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B. C.x2-y2 D.x2+y2
二.填空题(共5小题)
13.(2025春 青山区期中)如图, ABCD的对角线AC,BD相交于点O,且AC+BD=32,△AOB的周长为27,则CD= ______.
14.(2025春 海淀区校级期中)如图,在直角三角形ABC中,CD为斜边AB上的中线,点E是AB上方一点,且AE=BE,连接DE,若CD=3,AE=4,则DE的长为______.
15.如图,平行四边形ABCD,E是CD的中点,BE,AC相交于点O,若△COE的面积为1,则平行四边形ABCD的面积为 ______.
16.如图,在 ABCD中,AB=5,EF∥CD,点P是线段EF上的动点,连结AP,BP,S△ABP=10.当△ABP是以AB为腰的等腰三角形时,BP的长为______.
17.如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=4时,作FH⊥AG于H,连接DH,则:①点F是CD的中点;②DH=1;③;④∠ADH=45°.其中正确的结论有______.
三.解答题(共5小题)
18.如图,菱形ABCD的对角线AC、BD交于点O,E为OA中点.连接并延长DE至点F,使得EF=DE.连接AF、BF.
(1)求证:四边形AFBO是矩形;
(2)若∠ABC=60°,BF=1,求DF的长度.
19.如图,在△ABF中,E是AB的中点,延长BF至D,使得DF=BF,连接AD,延长EF至点C,使得CF=AD,连接CD.
(1)求证:四边形AFCD为平行四边形;
(2)连接AC交DB于点O,若CE⊥DB,EF=1,,求AF,AC的长.
20.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
21.如图,点E是矩形ABCD对角线AC上的点(不与A,C重合),连接BE,过点E作EF⊥BE交CD于点F.连接BF交AC于点G,BE=AD.
(1)求证:∠FEC=∠FCE;
(2)试判断线段BF与AC的位置关系,并说明理由.
22.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
沪科版八年级下 第19章 四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、C 3、B 4、C 5、C 6、A 7、C 8、C 9、B 10、D 11、A 12、B
二.填空题(共5小题)
13、11; 14、; 15、12; 16、5或; 17、①③④;
三.解答题(共5小题)
18、(1)证明:∵E为 AC的中点,EF=DE,
∴四边形ADOF是平行四边形,
∴AF=OD,AF∥OD,
∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD,
∴AF=OB,AF∥OB,
∴平行四边形AFBO是矩形;
(2)解:∵四边形AFBO是矩形,
∴∠FBD=90°,BF=OA=1,
∵∠ABC=60°,AB=BC,
∴∠ABO=30°,
∴OB=,
∴BD=2OB=2,
∴DF==.
19、(1)证明:∵DF=BF,
∴F是DB的中点,
∴E是AB的中点,
∴EF∥AD,
∵点C在EF的延长线上,
∴CF∥AD,
∵CF=AD,
∴四边形AFCD为平行四边形.
(2)解:∵DF=BF,AE=BE=,EF=1,
∴EF∥AD,且EF=AD,AB=2AE=2,
∴AD=2EF=2,
∵CE⊥DB于点F,
∴∠ADB=∠EFB=90°,
∴BD===6,
∴DF=BF=BD=3,
∴AF===,
∵四边形AFCD为平行四边形,
∴OD=OF=DF=,OA=OC,
∴OA===,
∴AC=2OA=5,
∴AF的长是,AC的长是5.
20、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO===2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB===2,
∴ ABCD的面积=AB AC=2×4=8.
21、(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠DCB=90°,
∵BE=AD,
∴BC=BE,
∴∠BEC=∠BCE,
∵EF⊥BE,
∴∠BEF=∠DCB=90°,
∴∠FEC=∠FCE;
(2)解:BF⊥AC.
理由:∵∠FEC=∠FCE,
∴EF=CF,
∵BE=BC,
∴BF垂直平分CE,
即BF⊥AC.
22、(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BEO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BC,连接AF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°-∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQ=PB,
∴==.
一.选择题(共12小题)
1.(2025春 青山区期中)如图,在 ABCD中,AB=AC,∠D=40°,则∠ACB的度数为( )
A.55° B.50° C.45° D.40°
2.(2025春 肥西县期中)如图,在Rt△ABC中,∠ABC=90°,点D是AC的中点,作AE⊥BD于点E,若DE=2BE,,则BC=( )
A. B.5 C. D.
3.(2025 蓝田县二模)如图,在 ABCD中,对角线AC交BD于O,已知AB=10,AC=12,BD=16,那么O到BC的距离为( )
A.4 B.4.8 C.5 D.6
4.如图,在 ABCD中,∠ABC的角平分线交AD于点E,若AB=3,ED=2,则BC的长度为( )
A.3 B.4 C.5 D.6
5.在 ABCD中,EF过对角线的交点O,AB=4,BC=5,OF=1.5,则四边形ABFE的周长是( )
A.11 B.11.5 C.12 D.12.5
6.如图,为了测量池塘边A,B两地之间的距离,在A,B的同侧取一点C,连接AC,BC,分别取AC,BC的中点D,E,测得DE=50m,则A,B之间的距离为( )
A.100m B.90m C.80m D.70m
7.如图,已知在 ABCD中,E,F是对角线BD上的两点,则以下条件不能判断四边形AECF为平行四边形的是( )
A.BE=DF B.AF⊥BD,CE⊥BD
C.AF=CE D.∠BAE=∠DCF
8.如图,平行四边形ABCD的对角线AC,BD相交于点O,点E,F分别是线段AO,BO的中点.若AC+BD=24cm,△OAB的周长是18cm,则EF的长为( )
A.2cm B.2.5cm C.3cm D.4cm
9.如图,已知在矩形ABCD中,AE⊥BD于点E,∠ABD=36°,则∠CAE的度数是( )
A.36° B.54° C.18° D.以上都不对
10.如图,在△ABC中,AB=AC=8,AN平分∠BAC交BC于点N,点M在BA上,且AM=3,连接CM,P为CM的中点,连接PN,则PN的长为( )
A.2.4 B.2 C.1.5 D.2.5
11.如图,在正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,EF.点P是EF的中点,连接CP,DP,若AE=AF,∠CPD=α,则∠CEF的度数为( )
A.α-45° B.135°-α C.2α-180° D.180°-α
12.(2025春 温州期中)如图,在 ABCD中,AC,BD相交于点O,过点A作AE⊥BC,AF⊥BD,AE=2AF,.记BE长为x,BO长为y(x≠0,y≠0).当x,y的值发生变化时,下列代数式的值不变的是( )
A.xy B. C.x2-y2 D.x2+y2
二.填空题(共5小题)
13.(2025春 青山区期中)如图, ABCD的对角线AC,BD相交于点O,且AC+BD=32,△AOB的周长为27,则CD= ______.
14.(2025春 海淀区校级期中)如图,在直角三角形ABC中,CD为斜边AB上的中线,点E是AB上方一点,且AE=BE,连接DE,若CD=3,AE=4,则DE的长为______.
15.如图,平行四边形ABCD,E是CD的中点,BE,AC相交于点O,若△COE的面积为1,则平行四边形ABCD的面积为 ______.
16.如图,在 ABCD中,AB=5,EF∥CD,点P是线段EF上的动点,连结AP,BP,S△ABP=10.当△ABP是以AB为腰的等腰三角形时,BP的长为______.
17.如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=4时,作FH⊥AG于H,连接DH,则:①点F是CD的中点;②DH=1;③;④∠ADH=45°.其中正确的结论有______.
三.解答题(共5小题)
18.如图,菱形ABCD的对角线AC、BD交于点O,E为OA中点.连接并延长DE至点F,使得EF=DE.连接AF、BF.
(1)求证:四边形AFBO是矩形;
(2)若∠ABC=60°,BF=1,求DF的长度.
19.如图,在△ABF中,E是AB的中点,延长BF至D,使得DF=BF,连接AD,延长EF至点C,使得CF=AD,连接CD.
(1)求证:四边形AFCD为平行四边形;
(2)连接AC交DB于点O,若CE⊥DB,EF=1,,求AF,AC的长.
20.如图,在 ABCD中,对角线AC,BD交于点O,AE⊥BD,CF⊥BD,垂足分别为E,F.
(1)求证:EO=FO;
(2)若AE=EF=4,求AC的长;
(3)若AC⊥AB,BD=2AC,当AC=4时,求 ABCD的面积.
21.如图,点E是矩形ABCD对角线AC上的点(不与A,C重合),连接BE,过点E作EF⊥BE交CD于点F.连接BF交AC于点G,BE=AD.
(1)求证:∠FEC=∠FCE;
(2)试判断线段BF与AC的位置关系,并说明理由.
22.如图,已知正方形ABCD中,E为CB延长线上一点,且BE=AB,M、N分别为AE、BC的中点,连DE交AB于O,MN交,ED于H点.
(1)求证:AO=BO;
(2)求证:∠HEB=∠HNB;
(3)过A作AP⊥ED于P点,连BP,则的值.
沪科版八年级下 第19章 四边形 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、C 3、B 4、C 5、C 6、A 7、C 8、C 9、B 10、D 11、A 12、B
二.填空题(共5小题)
13、11; 14、; 15、12; 16、5或; 17、①③④;
三.解答题(共5小题)
18、(1)证明:∵E为 AC的中点,EF=DE,
∴四边形ADOF是平行四边形,
∴AF=OD,AF∥OD,
∵四边形ABCD是菱形,
∴∠AOB=90°,OB=OD,
∴AF=OB,AF∥OB,
∴平行四边形AFBO是矩形;
(2)解:∵四边形AFBO是矩形,
∴∠FBD=90°,BF=OA=1,
∵∠ABC=60°,AB=BC,
∴∠ABO=30°,
∴OB=,
∴BD=2OB=2,
∴DF==.
19、(1)证明:∵DF=BF,
∴F是DB的中点,
∴E是AB的中点,
∴EF∥AD,
∵点C在EF的延长线上,
∴CF∥AD,
∵CF=AD,
∴四边形AFCD为平行四边形.
(2)解:∵DF=BF,AE=BE=,EF=1,
∴EF∥AD,且EF=AD,AB=2AE=2,
∴AD=2EF=2,
∵CE⊥DB于点F,
∴∠ADB=∠EFB=90°,
∴BD===6,
∴DF=BF=BD=3,
∴AF===,
∵四边形AFCD为平行四边形,
∴OD=OF=DF=,OA=OC,
∴OA===,
∴AC=2OA=5,
∴AF的长是,AC的长是5.
20、(1)证明:∵四边形ABCD是平行四边形,
∴AB=CD,AB∥CD,OB=OD,AO=CO,
∴∠ABE=∠CDF,
∵AE⊥BD,CF⊥BD,
∴∠AEB=∠CFD=90°,
在△ABE和△CDF中,
,
∴△ABE≌△CDF(AAS),
∴BE=DF,
∵OB=OD,
∴OB-BE=OD-DF,
∴OE=OF;
(2)解:∵AE=EF=4,OE=OF,
∴EO=OF=2,
∴AO===2,
∴AC=2AO=4;
(3)解:∵BD=2AC,AC=4,
∴BD=8,
∴BO=4,AO=2,
∵AC⊥AB,
∴AB===2,
∴ ABCD的面积=AB AC=2×4=8.
21、(1)证明:∵四边形ABCD是矩形,
∴AD=BC,∠DCB=90°,
∵BE=AD,
∴BC=BE,
∴∠BEC=∠BCE,
∵EF⊥BE,
∴∠BEF=∠DCB=90°,
∴∠FEC=∠FCE;
(2)解:BF⊥AC.
理由:∵∠FEC=∠FCE,
∴EF=CF,
∵BE=BC,
∴BF垂直平分CE,
即BF⊥AC.
22、(1)证明:∵四边形ABCD是正方形,
∴AD=AB,AD∥BC,
∴∠DAB=∠ABE,∠ADO=∠BEO,
∵AB=BE,
∴AD=BE,
∴△ADO≌△BEO(ASA),
∴AO=BO;
(2)证明:延长BC至F,且使CF=BC,连接AF,如图1所示:
则BF=CE,
∵四边形ABCD是矩形,
∴AB=DC,AD∥BC,∠BAD=∠ABC=∠DCB=90°,
在△ABF和△DCE中,,
∴△ABF≌△DCE(SAS),
∴∠DEC=∠AFB,
∵EB=CF,BN=CN,
∴N为EF的中点,
∴MN为△AEF的中位线,
∴MN∥AF,
∴∠HNB=∠AFB=∠HEB;
(3)解:过点B作BQ⊥BP交DE于Q,如图2所示:
则∠PBQ=90°,
∵∠ABE=180°-∠ABC=90°,
∴∠EBQ=∠ABP,
∵AD∥BC,
∴∠ADP=∠BEQ,
∵AP⊥DE,∠BAD=90°,
由角的互余关系得:∠BAP=∠ADP,
∴∠BEQ=∠BAP,
在△BEQ和△BAP中,,
∴△BEQ≌△BAP(ASA),
∴PA=QE,QB=PB,
∴△PBQ是等腰直角三角形,
∴PQ=PB,
∴==.
