沪科版数学九年级上册 21章 二次函数与反比例函数 单元测试(含答案)
文档属性
| 名称 | 沪科版数学九年级上册 21章 二次函数与反比例函数 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 118.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 00:00:00 | ||
图片预览



文档简介
沪科版九年级上 21章 二次函数与反比例函数 单元测试
一.选择题(共12小题)
1.(2025 双城区一模)二次函数y=5(x-1)2+2的顶点坐标是( )
A.(-1,2) B.(-1,-2) C.(1,-2) D.(1,2)
2.已知抛物线y=x2+2x-4与x轴交于点A(a,0)和B(b,0),则(a+1)(b+1)的值为( )
A.-5 B.-1 C.3 D.7
3.函数的图象经过点(2,m),则m的值为( )
A.3 B.-3 C.12 D.-12
4.在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
A.-1 B.1 C.2 D.3
5.点A(1,y1)和点B(3,y2)都在的图象上,则y1与y2的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.y1≥y2
6.如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c=m总有一正一负两个实数根,则m的取值范围是( )
A.m>3 B.m<3 C.m≥3 D.m≤3
7.已知函数中,在每个象限内,y随x的增大而增大,那么它和函数y=kx(k≠0)在同一直角坐标平面内的大致图象是( )
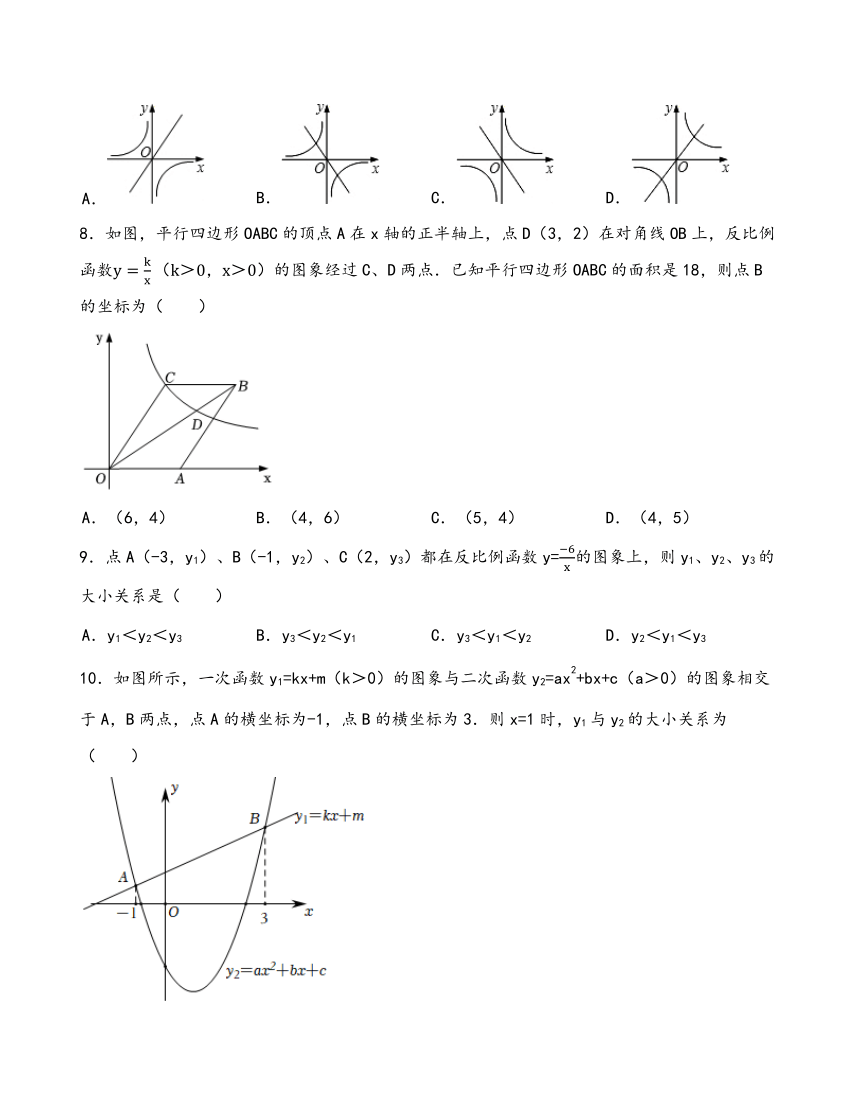
A. B. C. D.
8.如图,平行四边形OABC的顶点A在x轴的正半轴上,点D(3,2)在对角线OB上,反比例函数的图象经过C、D两点.已知平行四边形OABC的面积是18,则点B的坐标为( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
9.点A(-3,y1)、B(-1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
10.如图所示,一次函数y1=kx+m(k>0)的图象与二次函数y2=ax2+bx+c(a>0)的图象相交于A,B两点,点A的横坐标为-1,点B的横坐标为3.则x=1时,y1与y2的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法判断
11.如图,点A在反比例函数y1=(x>0)的图象上,过点A作AB⊥x轴,垂足为B,交反比例函数y2=(x>0)的图象于点C,连结OA,OC,则△AOC的面积为( )
A.3 B.4 C.5 D.6
12.如图是双曲线和双曲线的图象,设点A在C1上,AB⊥y轴于点B,交C2于点D,AC⊥x轴于点C,交C2于点E,则四边形ADOE的面积为( )
A.4 B.3 C.2 D.
二.填空题(共5小题)
13.如图,P是反比例函数图象上任意一点,过点P作x轴的垂线,垂足为A,则△PAO的面积为______.
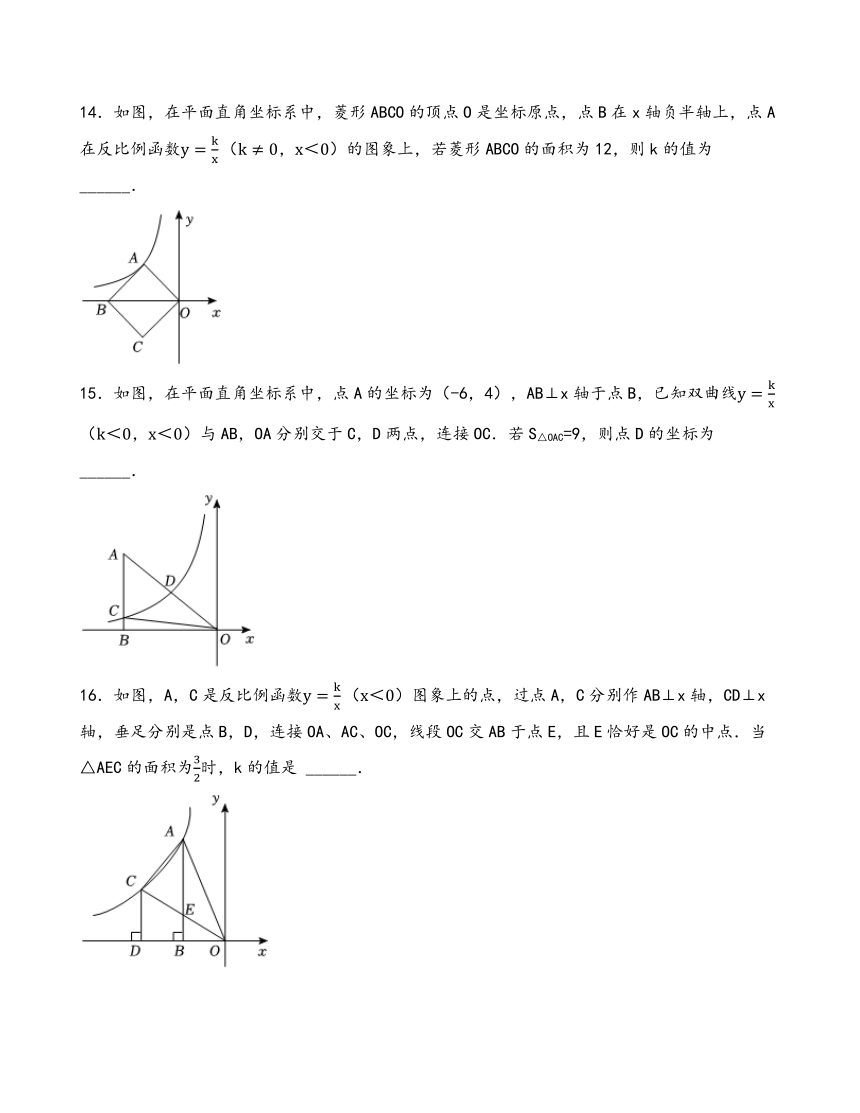
14.如图,在平面直角坐标系中,菱形ABCO的顶点O是坐标原点,点B在x轴负半轴上,点A在反比例函数的图象上,若菱形ABCO的面积为12,则k的值为______.
15.如图,在平面直角坐标系中,点A的坐标为(-6,4),AB⊥x轴于点B,已知双曲线与AB,OA分别交于C,D两点,连接OC.若S△OAC=9,则点D的坐标为______.
16.如图,A,C是反比例函数图象上的点,过点A,C分别作AB⊥x轴,CD⊥x轴,垂足分别是点B,D,连接OA、AC、OC,线段OC交AB于点E,且E恰好是OC的中点.当△AEC的面积为时,k的值是 ______.
17.如图,抛物线与x轴交于A,B两点,抛物线上点C的横坐标为5,D点坐标为(3,0),连接AC,CD,点M为平面内任意一点,将△ACD绕点M旋转180°得到对应的△A′C′D′(点A,C,D的对应点分别为点A′,C′,D′),若△A′C′D′中恰有两个点落在抛物线上,则此时点C'的坐标为 ______(点C'不与点A重合).
三.解答题(共5小题)
18.已知一次函数的图象与反比例函数的图象在第一象限交于点A(2,3)和点B(4,n),连接OA,过点B作BD⊥x轴,垂足为D,OA的延长线与直线BD交于点C.
(1)求一次函数和反比例函数的解析式;
(2)求△ABC的面积.
19.如图,一次函数y=k1x+b的图象与反比例函数的图象交于A(1,3),B(3,m)两点,k1,k2,b为常数.
(1)求一次函数和反比例函数的解析式;
(2)根据图象直接写出不等式的解集为 ______;
(3)点P为y轴上一点,若△PAB的面积为1,请直接写出点P的坐标.
20.(2025 鲁山县模拟)如图所示,反比例函数的图象与一次函数y2=kx+b(k≠0)的图象交于A(2,6),B(6,a)两点,在线段AB上取点P,过点P作x轴的垂线,垂足为C,交函数y1的图象于点D.
(1)求这两个函数的解析式;
(2)请直接写出不等式的取值范围______;
(3)若点P的横坐标为5,求△POD的面积.
21.如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(4,6),D是边CB上的一个动点(不与C、B重合),反比例函数(x>0)的图象经过点D且与边AB交于点E,连接DE.
(1)如图1,若点D是CB的中点,求E点的坐标;
(2)如图2,若直线DE与x轴、y轴分别交于M点,N点,过D作DP⊥x轴交于P点,过E作EQ⊥y轴交于Q点,DP与EQ交于点H,连接PQ,求证:DE∥PQ;
(3)如图3,将△BDE沿DE折叠,点B关于DE的对称点为点B′,当点B′落在矩形OABC内部时,求k的取值范围.
22.如图1,抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,作BC⊥x轴于点C.点D是抛物线上一点.
(1)求该抛物线的解析式;
(2)连接AD,交直线OB于点E,作EF⊥x轴,若EF=EB,求点E的坐标;
(3)若点P为抛物线上一点,且在第四象限内,已知直线PA,PB与x轴分别交于M、N两点,当点P运动时,是否为定值?若是,请求出该定值;若不是,请说明理由.
沪科版九年级上 21章 二次函数与反比例函数 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、B 4、A 5、A 6、A 7、B 8、A 9、C 10、A 11、D 12、C
二.填空题(共5小题)
13、1.5; 14、-6; 15、(-3,2); 16、-4; 17、(2,-3)或(-,-);
三.解答题(共5小题)
18、解:(1)∵一次函数y=ax+b的图象与反比例函数的图象在第一象限交于点A(2,3)和点B(4,n),
∴k=2×3=4n,
∴k=6,n=,
∴反比例函数的解析式为y=,
把A(2,3),B(4,)代入y=ax+b得,
解得,
∴一次函数的解析式为y=-x+;
(2)∵A(2,3),
∴直线OA的解析式为y=x,
∵过点B作BD⊥x轴,垂足为D,OA的延长线与直线BD交于点C,
∴C点的横坐标为4,
∴当x=4时,y==6,
∴C(4,6),
∴BC=6-=,
∴S△ABC==.
19、解:(1)将点A(1,3)代入之中,得:k2=3,
∴反比例函数的解析式为:y=,
将B(3,m)代入反比例函数y=之中,得:m=1,
∴点B的坐标为(3,1),
将点A(1,3),B(3,1)代入y=k1x+b之中,得:,
解得:,
∴一次函数的解析式为:y=-x+4.
(2)观察函数的图象可知:不等式的解集为:1<x<3或x<0.
(3)设P(0,n),
则直线BP为y=ax+n,
代入B(3,1)得:a=,
∴y=x+n,
过点A作AC⊥x轴于点C,交BP于点D,
∴D(1,),
∵△PAB的面积为1,
∴|3-|×3=1,
解得n=3或n=5,
∴点P的坐标为(0,3)或(0,5).
20、解:(1)∵A(2,6)在函数的图象上,
∴m=2×6=12.
∴反比例函数的解析式为,
∵点B(6,a)在反比例函数上,
∴.
∴B(6,2).
∵一次函数y2=kx+b过A(2,6),B(6,2),
∴
解得,
∴一次函数的解析式为y2=-x+8;
(2)∵A(2,6),B(6,2),
∴数形结合可得不等式的解集为0<x<2或x>6;
(3)当 x=5 时,
∴.P(5,3),D(5,2.4),C(5,0),
∴.
21、(1)解:∵四边形OABC是矩形,
∴BC∥x轴,AB∥y轴,
∵B(4,6),D是CB的中点,
∴D(2,6),
∵双曲线经过点D(2,6),
∴k=xy=2×6=12,
∴,
当x=4时,,
∴点E的坐标为(4,3);
(2)证明:∵点D、点E都在双曲线,
∴,E(4,),H(),
∴BD=,,QH=,,
∵DP⊥x轴,EQ⊥y轴,
∴四边形BDHE是矩形,
∴EH=BD=4-5,,
∴,,
∴,
又∵∠DHE=∠PHQ,
∴△DHE∽△PHQ,
∴∠HPQ=∠HDE,
∴DE∥PQ;
(3)解:如图,连接AC、BB'交于点I,BB'交DE于点F,
∵,
∴k随x的增大而增大,
∴当点B'在y轴上时,k的值最小;若点D与点B重合,则k的值最大,
∵DE垂直平分BB',DE∥AC,
∴∠BFD=∠BIC=∠BIA=90°,
∴∠B'BC=∠BAC=90°-∠ABB',
∵,
∴B'C2+CD2=B'D2,且 B'D=BD=4-CD,
∴,
解得:,
则点,
则,
若点D与点B重合,则k=xy=4×6=24,
∴k的取值范围是.
22、解:(1)抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,
∴,
解得:,
∴该抛物线的解析式为:y=x2-4x+3;
(2)∵B(4,3),
设直线OB的解析式为y=kx,
∴3=4k,
解得:,
∴直线OB的解析式为,
设,
∵EF=EB,
∴,
解得:或m=10(舍去),
∴;
(3)是定值,该定值为,理由如下.
令y=x2-4x+3=0,
解得x1=1,x2=3,即抛物线与x轴的交点是:(1,0)和(3,0),
设点P的坐标是(t,t2-4t+3),则1<t<3,
设直线AP的解析式是:y=k2x+b2,
将点A、P代入得:,
解得:,
∴直线AP的解析式是:y=(t-4)x+3,
令y=(t-4)x+3=0,
解得:,即,
∴,
设直线BP的解析式是:y=k3x+b3,
将点B、P代入得:,
解得:,
∴直线BP的解析式是:y=tx-4t+3,
令y=tx-4t+3=0,
解得:,即,
∴,,
∴.
∴是定值,该定值为.
一.选择题(共12小题)
1.(2025 双城区一模)二次函数y=5(x-1)2+2的顶点坐标是( )
A.(-1,2) B.(-1,-2) C.(1,-2) D.(1,2)
2.已知抛物线y=x2+2x-4与x轴交于点A(a,0)和B(b,0),则(a+1)(b+1)的值为( )
A.-5 B.-1 C.3 D.7
3.函数的图象经过点(2,m),则m的值为( )
A.3 B.-3 C.12 D.-12
4.在反比例函数的每一条曲线上,y都随着x的增大而减小,则k的值可以是( )
A.-1 B.1 C.2 D.3
5.点A(1,y1)和点B(3,y2)都在的图象上,则y1与y2的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.y1≥y2
6.如图,是二次函数y=ax2+bx+c的图象,若关于x的方程ax2+bx+c=m总有一正一负两个实数根,则m的取值范围是( )
A.m>3 B.m<3 C.m≥3 D.m≤3
7.已知函数中,在每个象限内,y随x的增大而增大,那么它和函数y=kx(k≠0)在同一直角坐标平面内的大致图象是( )
A. B. C. D.
8.如图,平行四边形OABC的顶点A在x轴的正半轴上,点D(3,2)在对角线OB上,反比例函数的图象经过C、D两点.已知平行四边形OABC的面积是18,则点B的坐标为( )
A.(6,4) B.(4,6) C.(5,4) D.(4,5)
9.点A(-3,y1)、B(-1,y2)、C(2,y3)都在反比例函数y=的图象上,则y1、y2、y3的大小关系是( )
A.y1<y2<y3 B.y3<y2<y1 C.y3<y1<y2 D.y2<y1<y3
10.如图所示,一次函数y1=kx+m(k>0)的图象与二次函数y2=ax2+bx+c(a>0)的图象相交于A,B两点,点A的横坐标为-1,点B的横坐标为3.则x=1时,y1与y2的大小关系为( )
A.y1>y2 B.y1<y2 C.y1=y2 D.无法判断
11.如图,点A在反比例函数y1=(x>0)的图象上,过点A作AB⊥x轴,垂足为B,交反比例函数y2=(x>0)的图象于点C,连结OA,OC,则△AOC的面积为( )
A.3 B.4 C.5 D.6
12.如图是双曲线和双曲线的图象,设点A在C1上,AB⊥y轴于点B,交C2于点D,AC⊥x轴于点C,交C2于点E,则四边形ADOE的面积为( )
A.4 B.3 C.2 D.
二.填空题(共5小题)
13.如图,P是反比例函数图象上任意一点,过点P作x轴的垂线,垂足为A,则△PAO的面积为______.
14.如图,在平面直角坐标系中,菱形ABCO的顶点O是坐标原点,点B在x轴负半轴上,点A在反比例函数的图象上,若菱形ABCO的面积为12,则k的值为______.
15.如图,在平面直角坐标系中,点A的坐标为(-6,4),AB⊥x轴于点B,已知双曲线与AB,OA分别交于C,D两点,连接OC.若S△OAC=9,则点D的坐标为______.
16.如图,A,C是反比例函数图象上的点,过点A,C分别作AB⊥x轴,CD⊥x轴,垂足分别是点B,D,连接OA、AC、OC,线段OC交AB于点E,且E恰好是OC的中点.当△AEC的面积为时,k的值是 ______.
17.如图,抛物线与x轴交于A,B两点,抛物线上点C的横坐标为5,D点坐标为(3,0),连接AC,CD,点M为平面内任意一点,将△ACD绕点M旋转180°得到对应的△A′C′D′(点A,C,D的对应点分别为点A′,C′,D′),若△A′C′D′中恰有两个点落在抛物线上,则此时点C'的坐标为 ______(点C'不与点A重合).
三.解答题(共5小题)
18.已知一次函数的图象与反比例函数的图象在第一象限交于点A(2,3)和点B(4,n),连接OA,过点B作BD⊥x轴,垂足为D,OA的延长线与直线BD交于点C.
(1)求一次函数和反比例函数的解析式;
(2)求△ABC的面积.
19.如图,一次函数y=k1x+b的图象与反比例函数的图象交于A(1,3),B(3,m)两点,k1,k2,b为常数.
(1)求一次函数和反比例函数的解析式;
(2)根据图象直接写出不等式的解集为 ______;
(3)点P为y轴上一点,若△PAB的面积为1,请直接写出点P的坐标.
20.(2025 鲁山县模拟)如图所示,反比例函数的图象与一次函数y2=kx+b(k≠0)的图象交于A(2,6),B(6,a)两点,在线段AB上取点P,过点P作x轴的垂线,垂足为C,交函数y1的图象于点D.
(1)求这两个函数的解析式;
(2)请直接写出不等式的取值范围______;
(3)若点P的横坐标为5,求△POD的面积.
21.如图,矩形OABC的顶点A、C分别在x轴和y轴上,点B的坐标为(4,6),D是边CB上的一个动点(不与C、B重合),反比例函数(x>0)的图象经过点D且与边AB交于点E,连接DE.
(1)如图1,若点D是CB的中点,求E点的坐标;
(2)如图2,若直线DE与x轴、y轴分别交于M点,N点,过D作DP⊥x轴交于P点,过E作EQ⊥y轴交于Q点,DP与EQ交于点H,连接PQ,求证:DE∥PQ;
(3)如图3,将△BDE沿DE折叠,点B关于DE的对称点为点B′,当点B′落在矩形OABC内部时,求k的取值范围.
22.如图1,抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,作BC⊥x轴于点C.点D是抛物线上一点.
(1)求该抛物线的解析式;
(2)连接AD,交直线OB于点E,作EF⊥x轴,若EF=EB,求点E的坐标;
(3)若点P为抛物线上一点,且在第四象限内,已知直线PA,PB与x轴分别交于M、N两点,当点P运动时,是否为定值?若是,请求出该定值;若不是,请说明理由.
沪科版九年级上 21章 二次函数与反比例函数 单元测试
(参考答案)
一.选择题(共12小题)
1、D 2、A 3、B 4、A 5、A 6、A 7、B 8、A 9、C 10、A 11、D 12、C
二.填空题(共5小题)
13、1.5; 14、-6; 15、(-3,2); 16、-4; 17、(2,-3)或(-,-);
三.解答题(共5小题)
18、解:(1)∵一次函数y=ax+b的图象与反比例函数的图象在第一象限交于点A(2,3)和点B(4,n),
∴k=2×3=4n,
∴k=6,n=,
∴反比例函数的解析式为y=,
把A(2,3),B(4,)代入y=ax+b得,
解得,
∴一次函数的解析式为y=-x+;
(2)∵A(2,3),
∴直线OA的解析式为y=x,
∵过点B作BD⊥x轴,垂足为D,OA的延长线与直线BD交于点C,
∴C点的横坐标为4,
∴当x=4时,y==6,
∴C(4,6),
∴BC=6-=,
∴S△ABC==.
19、解:(1)将点A(1,3)代入之中,得:k2=3,
∴反比例函数的解析式为:y=,
将B(3,m)代入反比例函数y=之中,得:m=1,
∴点B的坐标为(3,1),
将点A(1,3),B(3,1)代入y=k1x+b之中,得:,
解得:,
∴一次函数的解析式为:y=-x+4.
(2)观察函数的图象可知:不等式的解集为:1<x<3或x<0.
(3)设P(0,n),
则直线BP为y=ax+n,
代入B(3,1)得:a=,
∴y=x+n,
过点A作AC⊥x轴于点C,交BP于点D,
∴D(1,),
∵△PAB的面积为1,
∴|3-|×3=1,
解得n=3或n=5,
∴点P的坐标为(0,3)或(0,5).
20、解:(1)∵A(2,6)在函数的图象上,
∴m=2×6=12.
∴反比例函数的解析式为,
∵点B(6,a)在反比例函数上,
∴.
∴B(6,2).
∵一次函数y2=kx+b过A(2,6),B(6,2),
∴
解得,
∴一次函数的解析式为y2=-x+8;
(2)∵A(2,6),B(6,2),
∴数形结合可得不等式的解集为0<x<2或x>6;
(3)当 x=5 时,
∴.P(5,3),D(5,2.4),C(5,0),
∴.
21、(1)解:∵四边形OABC是矩形,
∴BC∥x轴,AB∥y轴,
∵B(4,6),D是CB的中点,
∴D(2,6),
∵双曲线经过点D(2,6),
∴k=xy=2×6=12,
∴,
当x=4时,,
∴点E的坐标为(4,3);
(2)证明:∵点D、点E都在双曲线,
∴,E(4,),H(),
∴BD=,,QH=,,
∵DP⊥x轴,EQ⊥y轴,
∴四边形BDHE是矩形,
∴EH=BD=4-5,,
∴,,
∴,
又∵∠DHE=∠PHQ,
∴△DHE∽△PHQ,
∴∠HPQ=∠HDE,
∴DE∥PQ;
(3)解:如图,连接AC、BB'交于点I,BB'交DE于点F,
∵,
∴k随x的增大而增大,
∴当点B'在y轴上时,k的值最小;若点D与点B重合,则k的值最大,
∵DE垂直平分BB',DE∥AC,
∴∠BFD=∠BIC=∠BIA=90°,
∴∠B'BC=∠BAC=90°-∠ABB',
∵,
∴B'C2+CD2=B'D2,且 B'D=BD=4-CD,
∴,
解得:,
则点,
则,
若点D与点B重合,则k=xy=4×6=24,
∴k的取值范围是.
22、解:(1)抛物线y=x2+bx+c经过A(0,3),B(4,3)两点,
∴,
解得:,
∴该抛物线的解析式为:y=x2-4x+3;
(2)∵B(4,3),
设直线OB的解析式为y=kx,
∴3=4k,
解得:,
∴直线OB的解析式为,
设,
∵EF=EB,
∴,
解得:或m=10(舍去),
∴;
(3)是定值,该定值为,理由如下.
令y=x2-4x+3=0,
解得x1=1,x2=3,即抛物线与x轴的交点是:(1,0)和(3,0),
设点P的坐标是(t,t2-4t+3),则1<t<3,
设直线AP的解析式是:y=k2x+b2,
将点A、P代入得:,
解得:,
∴直线AP的解析式是:y=(t-4)x+3,
令y=(t-4)x+3=0,
解得:,即,
∴,
设直线BP的解析式是:y=k3x+b3,
将点B、P代入得:,
解得:,
∴直线BP的解析式是:y=tx-4t+3,
令y=tx-4t+3=0,
解得:,即,
∴,,
∴.
∴是定值,该定值为.
