沪科版数学九年级上册 第22章 相似形 单元测试(含答案)
文档属性
| 名称 | 沪科版数学九年级上册 第22章 相似形 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 121.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 20:51:54 | ||
图片预览



文档简介
沪科版九年级上 第22章 相似形 单元测试
一.选择题(共12小题)
1.已知,则代数式的值为( )
A.1 B. C. D.
2.在△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,若,则CF的长为( )
A. B. C. D.
3.如图,在 ABCD中,点E为边AD上一点,连结BE交对角线AC于点G.若,AD=6,则DE的长为( )
A. B.4 C. D.5
4.如图,DE∥BC,BD,CE相交于O,,AE=4,则线段BE的长为( )
A.6 B.10 C.8 D.7
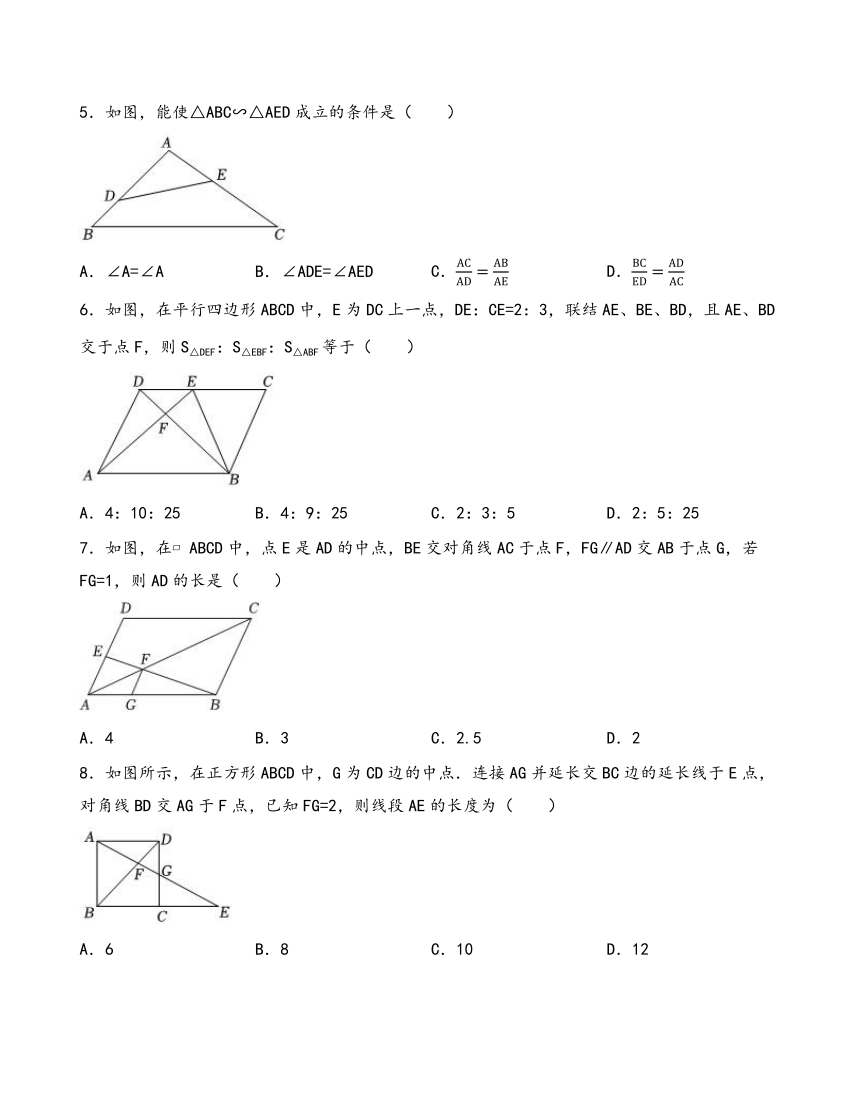
5.如图,能使△ABC∽△AED成立的条件是( )
A.∠A=∠A B.∠ADE=∠AED C. D.
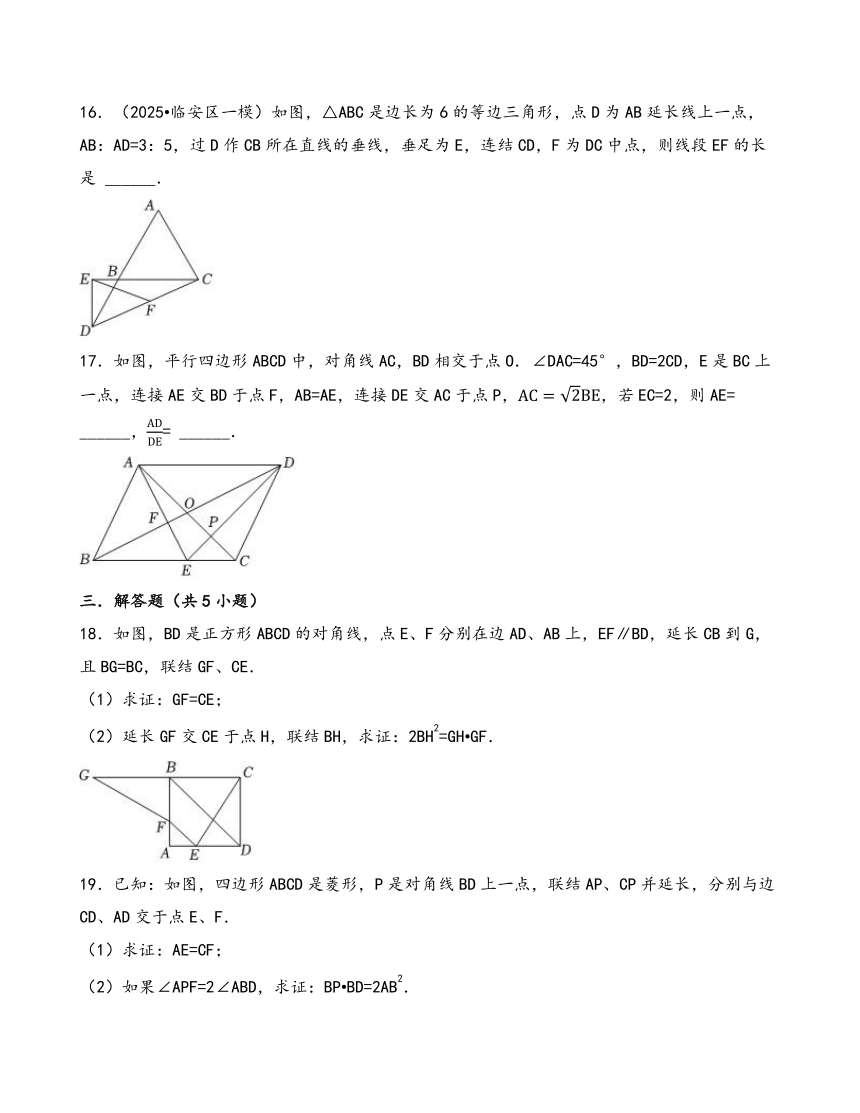
6.如图,在平行四边形ABCD中,E为DC上一点,DE:CE=2:3,联结AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
7.如图,在 ABCD中,点E是AD的中点,BE交对角线AC于点F,FG∥AD交AB于点G,若FG=1,则AD的长是( )
A.4 B.3 C.2.5 D.2
8.如图所示,在正方形ABCD中,G为CD边的中点.连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点,已知FG=2,则线段AE的长度为( )
A.6 B.8 C.10 D.12
9.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结BD交CH于点P,若△BPC为等腰三角形,则DH:HP的值是( )
A.2:1 B. C. D.
10.如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
11.如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
12.如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,在矩形ABCD中,点E,F分别在边BC,DC上,且AE⊥EF.若AB=2,AD=4,BE=1,则EF的长为______.
14.如图,在△ABC中,AC=BC=8,∠ACB=90°,点D、E分别为AC,BA的中点,点P从A点向D点运动,点Q在DE上,且DQ=DP,连接CQ,过点Q作QF⊥CQ交AB与点F,设点P运动的路程为x,△CQF的面积为y,则y与x之间关系为______.
15.如图,矩形护栏ABCD中,竖直方向加装4条平行且等距的钢条(任意相邻钢条间距相等,钢条粗细不计),连接AC交第一根钢条于点E,连接DE并延长交AB于点F,若AB=60cm,则AF的长度为______cm.
16.(2025 临安区一模)如图,△ABC是边长为6的等边三角形,点D为AB延长线上一点,AB:AD=3:5,过D作CB所在直线的垂线,垂足为E,连结CD,F为DC中点,则线段EF的长是 ______.
17.如图,平行四边形ABCD中,对角线AC,BD相交于点O.∠DAC=45°,BD=2CD,E是BC上一点,连接AE交BD于点F,AB=AE,连接DE交AC于点P,,若EC=2,则AE= ______,= ______.
三.解答题(共5小题)
18.如图,BD是正方形ABCD的对角线,点E、F分别在边AD、AB上,EF∥BD,延长CB到G,且BG=BC,联结GF、CE.
(1)求证:GF=CE;
(2)延长GF交CE于点H,联结BH,求证:2BH2=GH GF.
19.已知:如图,四边形ABCD是菱形,P是对角线BD上一点,联结AP、CP并延长,分别与边CD、AD交于点E、F.
(1)求证:AE=CF;
(2)如果∠APF=2∠ABD,求证:BP BD=2AB2.
20.如图1,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.
(1)若BF=5,DC=2,求AB的长.
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,两条垂线交于点G,连接BG,如图2.求证:.
21.已知:如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:△ABC∽△GDF;
(2)当点E为AC的中点时,求证:.
22.已知△ABC中,∠ABC=2∠C,BG平分∠ABC,AB=8,AG=.点D、E分别是边BC、AC上的点(点D不与点B、C重合),且∠ADE=∠ABC,AD、BG相交于点F.
(1)求BC的长;
(2)如图1,如果BF=2CE,求BF:GF的值;
(3)如果△ADE是以AD为腰的等腰三角形,求BD长.
沪科版九年级上 第22章 相似形 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、C 3、B 4、A 5、C 6、A 7、B 8、D 9、C 10、D 11、D 12、B
二.填空题(共5小题)
13、; 14、; 15、15; 16、; 17、;;
三.解答题(共5小题)
18、证明:(1)∵四边形ABCD是正方形,
∴∠ABC=∠CDA=90°,AB=AD,
∴∠GBF=∠CDE=90°,∠ABD=∠ADB,
∵EF∥BD,
∴∠AFE=∠ABD,∠AEF=∠ADB,
∴∠AFE=∠AEF,
∴AF=AE,
∴AB-AF=AD-AE,
∴BF=DE,
∵BG=BC,DC=BC,
∴BG=DC,
在△GBF和△CDE中,
,
∴△GBF≌△CDE(SAS),
∴GF=CE.
(2)延长GF交CE于点H,联结BH,
∵BC∥AD,
∴∠GCH=∠CED,
由(1)得△GBF≌△CDE,
∴∠G=∠DCE,
∴∠G+∠GCH=∠DCE+∠CED=90°,
∴∠GHC=180°-(∠G+∠GCH)=90°,
∴BH=GB=GC,
∴GC=2BH,
∴GC GB=2BH BH=2BH2,
∵∠GBF=∠GHC=90°,∠G=∠G,
∴△GBF∽△GHC,
∴=,
∴GC GB=GH GF,
∴2BH2=GH GF.
19、证明:(1)∵四边形ABCD是菱形,
∴AD=CD,BD垂直平分AC,
∴∠ACD=∠CAD,
∵点P在BD上,
∴PA=PC,
∴∠PAC=∠PCA,
在△ACE和△CAF中,
,
∴△ACE≌△CAF(ASA),
∴AE=CF.
(2)设AC交BD于点L,则LB=LD=BD,
∵AB=CB,BD⊥AC,
∴∠ABD=∠CBD,
∴∠ABC=2∠ABD,
∵∠APF=2∠ABD,
∴∠APF=∠ABC,
∴∠ABC+∠APC=∠APF+∠APC=180°,
∴∠BAP+∠BCP=360°-(∠ABC+∠APC)=180°,
∵∠BAC=∠BCA,∠PAC=∠PCA,
∴∠BAP=∠BAC+∠PAC=∠BCA+∠PCA=∠BCP,
∴2∠BAP=180°,
∴∠BLA=∠BAP=90°,
∵∠ABL=∠PBA,
∴△ABL∽△PBA,
∴=,
∴=,
∴BP BD=2AB2.
20、(1)解:∵AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF=∠DAC=90°-∠C,
∵∠ADB=90°,∠ABC=45°,
∴∠BAD=∠ABD=45°,
∴BD=AD,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA),
∴DF=DC=2,
∵BF=5,
∴BD2=BF2-DF2=52-22=21,
∴AB====,
∴AB的长为.
(2)证明:如图2,作FH∥BD交AB于点H,则∠AFH=∠ADB=90°,∠AHF=∠ABD=∠HAF,
∴AF=HF,
∴AH==AF,
∵GF⊥BF,AG⊥AB,
∴∠GFB=∠GAB=90°,
∴∠AFG=∠HFB=90°-∠GFH,∠BLG=∠AGF+90°=∠HBF+90°,
∴∠AGF=∠HBF,
在△AGF和△HBF中,
,
∴△AGF≌△HBF(AAS),
∴AG=HB,
∴AB=HB+AH=AG+AF.
21、证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴△BAC∽△BCF,
∵DE∥BC,
∴△BCF∽△DGF,
∴△DGF∽△BAC.
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
∴AH=2EG,
∵AH∥DG,
∴△AHF∽△DGF,
∴=,
∴.
22、解:(1)∵∠ABC=2∠C,BG平分∠ABC,
∴∠ABG=∠BGC=∠C,
∴BG=CG,
又∵∠BAG=∠CAB,
∴△ABG∽△ACB,
∴==,
∴AC===12,
∴CG=AC-AG=,
∴BC==10;
(2)由(1)知,△ABG∽△CAB,
∴∠AGB=∠ABC,
∵∠ADE=∠ABC,
∴∠AGB=∠ADE,
∵∠FAG=∠DAE,
∴∠AFG=∠AED,
∵∠AFG+∠AFB=180°,∠AED+∠CED=180°,
∴∠AFG=∠CED,
又∵∠ABG=∠C,
∴△ABF∽△DCE,
∴==2,
∴CD=4,
∴BD=BC-CD=6,
过G作HG∥BC交AD于H,如图:
∴=,
∴GH==,
同理,==,
∴BF:FG=;
(3)∵AD=AE,
∴∠ADE=∠AED=∠ABC=∠AGB,
∴DE∥BG,
∴∠AFG=∠ADE=∠AGF,
∴AF=AG,
∵∠ABC=2∠C,
∴∠EDC=∠C,
∴CE=DE,
由(2)知,△ABF∽△CDE,
∴AF=BF,
∴GF=BG-BF=CG-AG=,
∵DE∥BG,
∴=,
∴DE=CE=,
同理,=,
∴CD=,
∴BD=.
另外,DA=DE时,作CE中垂线交BC于点H,同理可证得△ABD≌△DHE.此时BD=1.
一.选择题(共12小题)
1.已知,则代数式的值为( )
A.1 B. C. D.
2.在△ABC中,∠ABC=90°,BD⊥AC,点E为BD的中点,连接AE并延长交BC于点F,且有AF=CF,若,则CF的长为( )
A. B. C. D.
3.如图,在 ABCD中,点E为边AD上一点,连结BE交对角线AC于点G.若,AD=6,则DE的长为( )
A. B.4 C. D.5
4.如图,DE∥BC,BD,CE相交于O,,AE=4,则线段BE的长为( )
A.6 B.10 C.8 D.7
5.如图,能使△ABC∽△AED成立的条件是( )
A.∠A=∠A B.∠ADE=∠AED C. D.
6.如图,在平行四边形ABCD中,E为DC上一点,DE:CE=2:3,联结AE、BE、BD,且AE、BD交于点F,则S△DEF:S△EBF:S△ABF等于( )
A.4:10:25 B.4:9:25 C.2:3:5 D.2:5:25
7.如图,在 ABCD中,点E是AD的中点,BE交对角线AC于点F,FG∥AD交AB于点G,若FG=1,则AD的长是( )
A.4 B.3 C.2.5 D.2
8.如图所示,在正方形ABCD中,G为CD边的中点.连接AG并延长交BC边的延长线于E点,对角线BD交AG于F点,已知FG=2,则线段AE的长度为( )
A.6 B.8 C.10 D.12
9.如图,四个全等的直角三角形拼成“赵爽弦图”,得到正方形ABCD与正方形EFGH,连结BD交CH于点P,若△BPC为等腰三角形,则DH:HP的值是( )
A.2:1 B. C. D.
10.如图,DE是△ABC的中位线,点F为DE上一点,且EF=2DF,CF的延长线交AB于点G,若DG=1,则AG的长为( )
A.2 B. C.3 D.4
11.如图,在正方形ABCD中,对角线AC,BD相交于点O,E是OD的中点,连接CE,过点E作EG⊥EC,EG与AC,AB分别交于点F,G,若EC=EG,则的长为( )
A. B. C.2 D.
12.如图,在正方形ABCD中,AB=5,E为边CD上一动点(不与端点重合),AE交BD于点F,过点F作FH⊥AE交BC于点H,过点H作HG⊥BD于点G,连接AH,HE.给出下列结论:①AF=HE;②∠HAE=45°;③;④,其中正确的个数有( )
A.1个 B.2个 C.3个 D.4个
二.填空题(共5小题)
13.如图,在矩形ABCD中,点E,F分别在边BC,DC上,且AE⊥EF.若AB=2,AD=4,BE=1,则EF的长为______.
14.如图,在△ABC中,AC=BC=8,∠ACB=90°,点D、E分别为AC,BA的中点,点P从A点向D点运动,点Q在DE上,且DQ=DP,连接CQ,过点Q作QF⊥CQ交AB与点F,设点P运动的路程为x,△CQF的面积为y,则y与x之间关系为______.
15.如图,矩形护栏ABCD中,竖直方向加装4条平行且等距的钢条(任意相邻钢条间距相等,钢条粗细不计),连接AC交第一根钢条于点E,连接DE并延长交AB于点F,若AB=60cm,则AF的长度为______cm.
16.(2025 临安区一模)如图,△ABC是边长为6的等边三角形,点D为AB延长线上一点,AB:AD=3:5,过D作CB所在直线的垂线,垂足为E,连结CD,F为DC中点,则线段EF的长是 ______.
17.如图,平行四边形ABCD中,对角线AC,BD相交于点O.∠DAC=45°,BD=2CD,E是BC上一点,连接AE交BD于点F,AB=AE,连接DE交AC于点P,,若EC=2,则AE= ______,= ______.
三.解答题(共5小题)
18.如图,BD是正方形ABCD的对角线,点E、F分别在边AD、AB上,EF∥BD,延长CB到G,且BG=BC,联结GF、CE.
(1)求证:GF=CE;
(2)延长GF交CE于点H,联结BH,求证:2BH2=GH GF.
19.已知:如图,四边形ABCD是菱形,P是对角线BD上一点,联结AP、CP并延长,分别与边CD、AD交于点E、F.
(1)求证:AE=CF;
(2)如果∠APF=2∠ABD,求证:BP BD=2AB2.
20.如图1,在锐角△ABC中,∠ABC=45°,AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F.
(1)若BF=5,DC=2,求AB的长.
(2)在图1上过点F作BE的垂线,过点A作AB的垂线,两条垂线交于点G,连接BG,如图2.求证:.
21.已知:如图,在△ABC中,点D,E分别在AB,AC上,DE∥BC,点F在边AB上,BC2=BF BA,CF与DE相交于点G.
(1)求证:△ABC∽△GDF;
(2)当点E为AC的中点时,求证:.
22.已知△ABC中,∠ABC=2∠C,BG平分∠ABC,AB=8,AG=.点D、E分别是边BC、AC上的点(点D不与点B、C重合),且∠ADE=∠ABC,AD、BG相交于点F.
(1)求BC的长;
(2)如图1,如果BF=2CE,求BF:GF的值;
(3)如果△ADE是以AD为腰的等腰三角形,求BD长.
沪科版九年级上 第22章 相似形 单元测试
(参考答案)
一.选择题(共12小题)
1、B 2、C 3、B 4、A 5、C 6、A 7、B 8、D 9、C 10、D 11、D 12、B
二.填空题(共5小题)
13、; 14、; 15、15; 16、; 17、;;
三.解答题(共5小题)
18、证明:(1)∵四边形ABCD是正方形,
∴∠ABC=∠CDA=90°,AB=AD,
∴∠GBF=∠CDE=90°,∠ABD=∠ADB,
∵EF∥BD,
∴∠AFE=∠ABD,∠AEF=∠ADB,
∴∠AFE=∠AEF,
∴AF=AE,
∴AB-AF=AD-AE,
∴BF=DE,
∵BG=BC,DC=BC,
∴BG=DC,
在△GBF和△CDE中,
,
∴△GBF≌△CDE(SAS),
∴GF=CE.
(2)延长GF交CE于点H,联结BH,
∵BC∥AD,
∴∠GCH=∠CED,
由(1)得△GBF≌△CDE,
∴∠G=∠DCE,
∴∠G+∠GCH=∠DCE+∠CED=90°,
∴∠GHC=180°-(∠G+∠GCH)=90°,
∴BH=GB=GC,
∴GC=2BH,
∴GC GB=2BH BH=2BH2,
∵∠GBF=∠GHC=90°,∠G=∠G,
∴△GBF∽△GHC,
∴=,
∴GC GB=GH GF,
∴2BH2=GH GF.
19、证明:(1)∵四边形ABCD是菱形,
∴AD=CD,BD垂直平分AC,
∴∠ACD=∠CAD,
∵点P在BD上,
∴PA=PC,
∴∠PAC=∠PCA,
在△ACE和△CAF中,
,
∴△ACE≌△CAF(ASA),
∴AE=CF.
(2)设AC交BD于点L,则LB=LD=BD,
∵AB=CB,BD⊥AC,
∴∠ABD=∠CBD,
∴∠ABC=2∠ABD,
∵∠APF=2∠ABD,
∴∠APF=∠ABC,
∴∠ABC+∠APC=∠APF+∠APC=180°,
∴∠BAP+∠BCP=360°-(∠ABC+∠APC)=180°,
∵∠BAC=∠BCA,∠PAC=∠PCA,
∴∠BAP=∠BAC+∠PAC=∠BCA+∠PCA=∠BCP,
∴2∠BAP=180°,
∴∠BLA=∠BAP=90°,
∵∠ABL=∠PBA,
∴△ABL∽△PBA,
∴=,
∴=,
∴BP BD=2AB2.
20、(1)解:∵AD⊥BC于点D,BE⊥AC于点E,BE与AD交于点F,
∴∠BDF=∠ADC=∠BEC=90°,
∴∠DBF=∠DAC=90°-∠C,
∵∠ADB=90°,∠ABC=45°,
∴∠BAD=∠ABD=45°,
∴BD=AD,
在△BDF和△ADC中,
,
∴△BDF≌△ADC(ASA),
∴DF=DC=2,
∵BF=5,
∴BD2=BF2-DF2=52-22=21,
∴AB====,
∴AB的长为.
(2)证明:如图2,作FH∥BD交AB于点H,则∠AFH=∠ADB=90°,∠AHF=∠ABD=∠HAF,
∴AF=HF,
∴AH==AF,
∵GF⊥BF,AG⊥AB,
∴∠GFB=∠GAB=90°,
∴∠AFG=∠HFB=90°-∠GFH,∠BLG=∠AGF+90°=∠HBF+90°,
∴∠AGF=∠HBF,
在△AGF和△HBF中,
,
∴△AGF≌△HBF(AAS),
∴AG=HB,
∴AB=HB+AH=AG+AF.
21、证明:(1)∵BC2=BF BA,
∴BC:BF=BA:BC,
而∠ABC=∠CBF,
∴△BAC∽△BCF,
∵DE∥BC,
∴△BCF∽△DGF,
∴△DGF∽△BAC.
(2)作AH∥BC交CF的延长线于H,如图,
∵DE∥BC,
∴AH∥DE,
∵点E为AC的中点,
∴AH=2EG,
∵AH∥DG,
∴△AHF∽△DGF,
∴=,
∴.
22、解:(1)∵∠ABC=2∠C,BG平分∠ABC,
∴∠ABG=∠BGC=∠C,
∴BG=CG,
又∵∠BAG=∠CAB,
∴△ABG∽△ACB,
∴==,
∴AC===12,
∴CG=AC-AG=,
∴BC==10;
(2)由(1)知,△ABG∽△CAB,
∴∠AGB=∠ABC,
∵∠ADE=∠ABC,
∴∠AGB=∠ADE,
∵∠FAG=∠DAE,
∴∠AFG=∠AED,
∵∠AFG+∠AFB=180°,∠AED+∠CED=180°,
∴∠AFG=∠CED,
又∵∠ABG=∠C,
∴△ABF∽△DCE,
∴==2,
∴CD=4,
∴BD=BC-CD=6,
过G作HG∥BC交AD于H,如图:
∴=,
∴GH==,
同理,==,
∴BF:FG=;
(3)∵AD=AE,
∴∠ADE=∠AED=∠ABC=∠AGB,
∴DE∥BG,
∴∠AFG=∠ADE=∠AGF,
∴AF=AG,
∵∠ABC=2∠C,
∴∠EDC=∠C,
∴CE=DE,
由(2)知,△ABF∽△CDE,
∴AF=BF,
∴GF=BG-BF=CG-AG=,
∵DE∥BG,
∴=,
∴DE=CE=,
同理,=,
∴CD=,
∴BD=.
另外,DA=DE时,作CE中垂线交BC于点H,同理可证得△ABD≌△DHE.此时BD=1.
