青岛版数学八年级下册 第6章 平行四边形 单元测试(含答案)
文档属性
| 名称 | 青岛版数学八年级下册 第6章 平行四边形 单元测试(含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 144.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-20 20:53:46 | ||
图片预览



文档简介
青岛版八年级下 第6章 平行四边形
一.选择题(共12小题)
1.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
2.如图,两条直线相交于点O,所夹锐角为60°,以点O为圆心,任意长为半径作圆,与两条直线分别交于点A、B、C、D,下列说法不正确的是( )
A.AB=2BC B.AC=BD C.∠ABC=90° D.∠OBC=∠OAD
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E在线段BO上,连接AE,若5BE=3CD,∠DAE=∠DEA,EO=1,则菱形ABCD的面积等于( )
A.12 B.24 C.48 D.96
4.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若AC=8,S菱形ABCD=24,则OH的长为( )
A.3 B.4 C.4.8 D.5
5.如图,在正方形ABCD中AB=6,点E是对角线AC上的一点,连结DE,过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连结AG,若F恰为AB的中点,则AG的长为( )
A. B. C. D.
6.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为( )
A.1.5 B.1.25 C.1 D.0.75
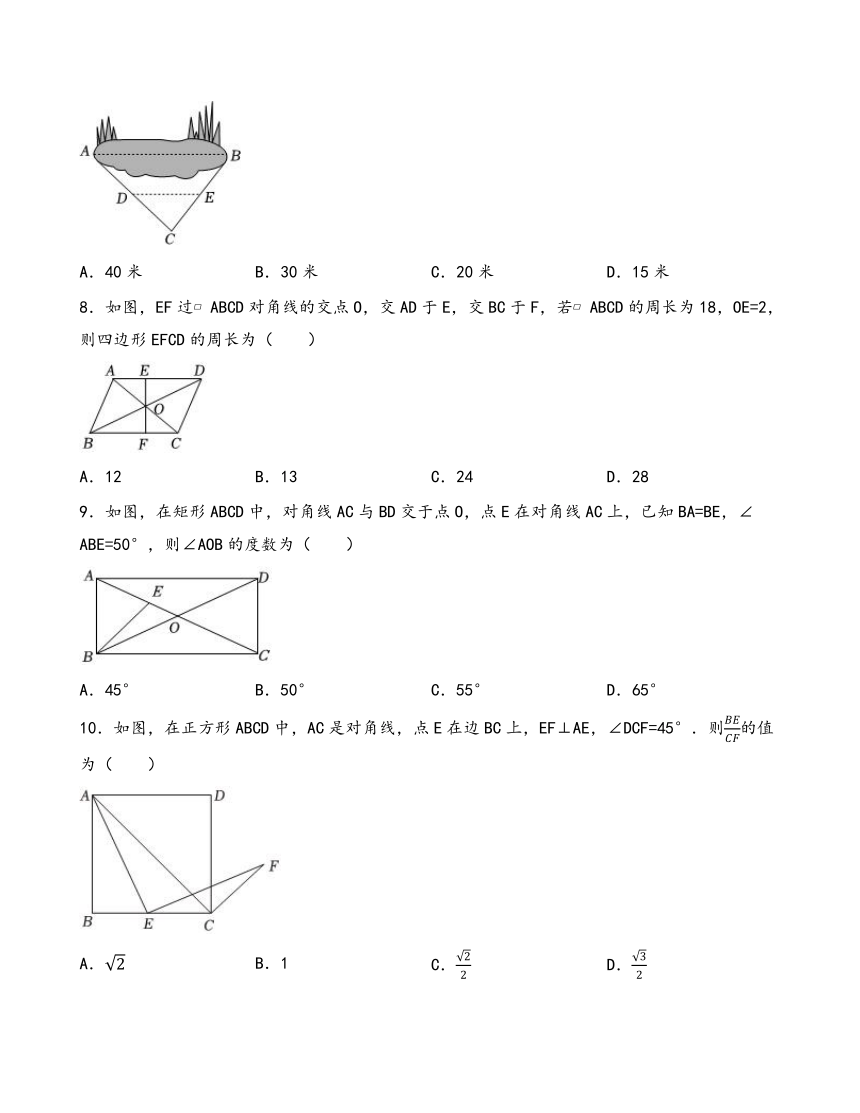
7.如图,小红想测量池塘两端A,B的距离,他采用了如下方法:在AB的一侧选择一点C,连接AC,BC,再分别找出AC,BC的中点D,E,连接DE,现测得DE=10米,则A,B之间的距离为( )
A.40米 B.30米 C.20米 D.15米
8.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=2,则四边形EFCD的周长为( )
A.12 B.13 C.24 D.28
9.如图,在矩形ABCD中,对角线AC与BD交于点O,点E在对角线AC上,已知BA=BE,∠ABE=50°,则∠AOB的度数为( )
A.45° B.50° C.55° D.65°
10.如图,在正方形ABCD中,AC是对角线,点E在边BC上,EF⊥AE,∠DCF=45°.则的值为( )
A. B.1 C. D.
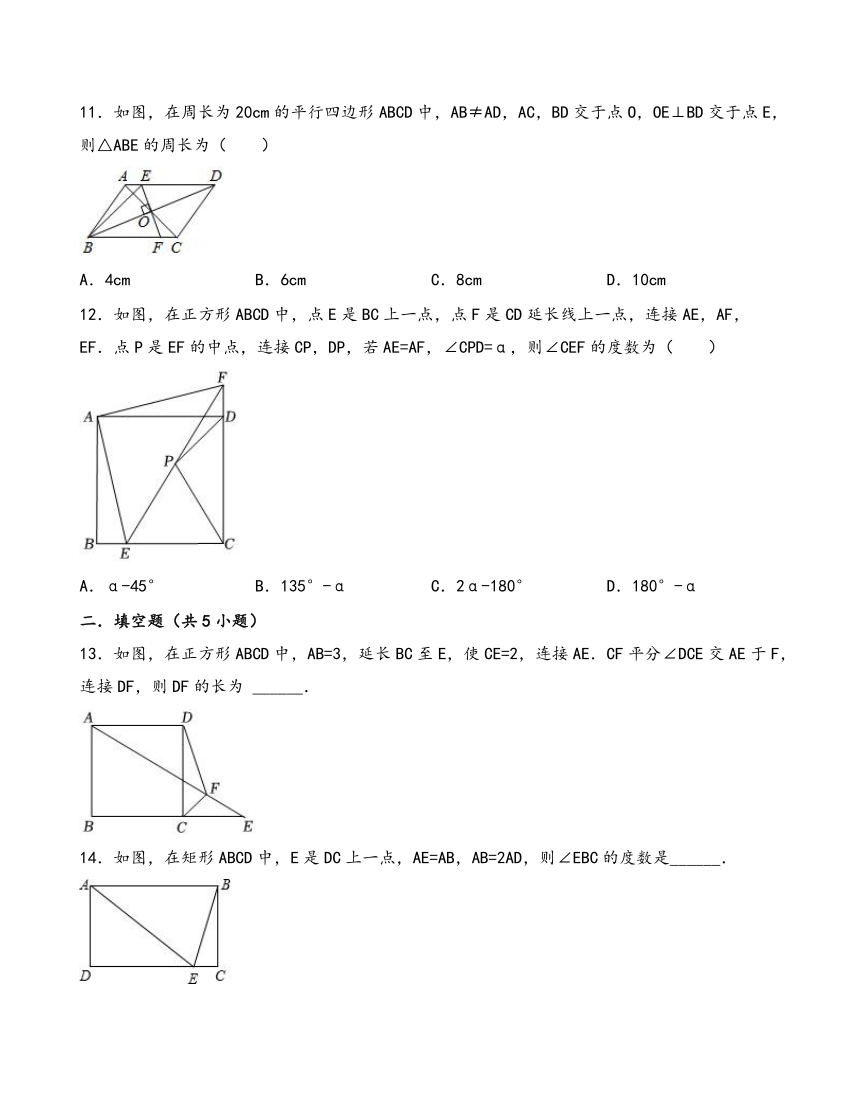
11.如图,在周长为20cm的平行四边形ABCD中,AB≠AD,AC,BD交于点O,OE⊥BD交于点E,则△ABE的周长为( )
A.4cm B.6cm C.8cm D.10cm
12.如图,在正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,EF.点P是EF的中点,连接CP,DP,若AE=AF,∠CPD=α,则∠CEF的度数为( )
A.α-45° B.135°-α C.2α-180° D.180°-α
二.填空题(共5小题)
13.如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 ______.
14.如图,在矩形ABCD中,E是DC上一点,AE=AB,AB=2AD,则∠EBC的度数是______.
15.如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,AC=8,DE⊥BC于点E,连接OE,则OE的长度为______.
16.如图,正方形ABCD的边长为6,点E,F分别是边BC,CD上的点,且BE=CF=2,
连接AE,AF,AE的垂直平分线分别交AB,AE,AF,CD于点G,M,N,H,则MN的长为 ______.
17.如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=4时,作FH⊥AG于H,连接DH,则:①点F是CD的中点;②DH=1;③;④∠ADH=45°.其中正确的结论有______.
三.解答题(共5小题)
18.如图,在 ABCD中,AD>AB,AE平分∠BAD,交BC于点E,过点E作EF∥AB交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,∠EBA=120°,求AE的大小.
19.如图,在 ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=4,EC=3,∠BAE=30°,求OF的长度.
20.如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若BD=10,AD=13,求线段OE的长.
21.如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
22.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
青岛版八年级下 第6章 平行四边形
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、B 4、A 5、D 6、A 7、C 8、B 9、B 10、C 11、D 12、A
二.填空题(共5小题)
13、; 14、15°; 15、3; 16、; 17、①③④;
三.解答题(共5小题)
18、(1)证明:∵ ABCD
∴BC∥AD,即 BE∥AF
∵EF∥AB
∴四边形ABEF为平行四边形
∵AE平分∠BAF
∴∠EAB=∠EAF
∵BC∥AD
∴∠BEA=∠EAF
∴∠BEA=∠BAE
∴AB=BE
∴四边形ABEF是菱形
(2)解:连接BF交AE于点O;则BF⊥AE于点O
∵BA=BE,∠EBA=120°
∴∠BEA=∠BAE=30°
∵菱形ABEF的周长为16
∴AB=4
在Rt△ABO中∠BAO=30°
∴
由勾股定理可得:AO=
∴AE=
19、(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=4,
∵EC=3,
∴BE=CF=1,
∴BF=5,
Rt△ABE中,∠BAE=30°,
∴AB=2BE=2,
∴DF=AE==,
∴BD===2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
20、(1)证明:∵四边形ABCD是菱形,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形;
(2)解:如图,∵四边形ABCD是菱形,
∴OB=OD=BD=5,OA=OC,AC⊥BD,
∴OA===12,
∴AC=2OA=24,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=12.
21、(1)证明:过点F作FK⊥AB于点K,如图所示:
∴∠FKH=∠FKA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠D=90°,
∴∠FKA=∠BAD=∠D=90°,∠B=∠FKH=90°,
∴四边形ADFK是矩形,
∴AD=FK,DF=AK,
∴AB=FK,
∵FH⊥AE,∠FKH=90°,
∴∠BAE+∠AHF=90°,∠KFH+∠AHF=90°,
∴∠BAE=∠KFH,
在△BAE和△KFH中,
,
∴△BAE≌△KFH(ASA),
∴AE=HF;
(2)解:AH与BE之间的数量关系是,AH=2BE,证明如下:
∵△BAE≌△KFH,
∴BE=KH,
又∵BE=DF,DF=AK,
∴AK=BE,
∴AH=AK+KH=BE+BE=2BE.
22、(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°-∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=AC=AB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG===3,
∴DE=EG=3.
∴正方形DEFG的边长为3.
一.选择题(共12小题)
1.已知四边形ABCD中,∠A=∠B=∠C=90°,如果添加一个条件,使得该四边形成为正方形,那么所添加的这个条件可以是( )
A.∠D=90° B.AB=CD C.AB=BC D.AC=BD
2.如图,两条直线相交于点O,所夹锐角为60°,以点O为圆心,任意长为半径作圆,与两条直线分别交于点A、B、C、D,下列说法不正确的是( )
A.AB=2BC B.AC=BD C.∠ABC=90° D.∠OBC=∠OAD
3.如图,在菱形ABCD中,对角线AC,BD相交于点O,点E在线段BO上,连接AE,若5BE=3CD,∠DAE=∠DEA,EO=1,则菱形ABCD的面积等于( )
A.12 B.24 C.48 D.96
4.如图,菱形ABCD的对角线AC,BD相交于点O,过点D作DH⊥AB于点H,连接OH,若AC=8,S菱形ABCD=24,则OH的长为( )
A.3 B.4 C.4.8 D.5
5.如图,在正方形ABCD中AB=6,点E是对角线AC上的一点,连结DE,过点E作EF⊥ED,交AB于点F,以DE,EF为邻边作矩形DEFG,连结AG,若F恰为AB的中点,则AG的长为( )
A. B. C. D.
6.如图,△ABC中,AD是中线,AE是角平分线,CF⊥AE于F,AB=5,AC=2,则DF的长为( )
A.1.5 B.1.25 C.1 D.0.75
7.如图,小红想测量池塘两端A,B的距离,他采用了如下方法:在AB的一侧选择一点C,连接AC,BC,再分别找出AC,BC的中点D,E,连接DE,现测得DE=10米,则A,B之间的距离为( )
A.40米 B.30米 C.20米 D.15米
8.如图,EF过 ABCD对角线的交点O,交AD于E,交BC于F,若 ABCD的周长为18,OE=2,则四边形EFCD的周长为( )
A.12 B.13 C.24 D.28
9.如图,在矩形ABCD中,对角线AC与BD交于点O,点E在对角线AC上,已知BA=BE,∠ABE=50°,则∠AOB的度数为( )
A.45° B.50° C.55° D.65°
10.如图,在正方形ABCD中,AC是对角线,点E在边BC上,EF⊥AE,∠DCF=45°.则的值为( )
A. B.1 C. D.
11.如图,在周长为20cm的平行四边形ABCD中,AB≠AD,AC,BD交于点O,OE⊥BD交于点E,则△ABE的周长为( )
A.4cm B.6cm C.8cm D.10cm
12.如图,在正方形ABCD中,点E是BC上一点,点F是CD延长线上一点,连接AE,AF,EF.点P是EF的中点,连接CP,DP,若AE=AF,∠CPD=α,则∠CEF的度数为( )
A.α-45° B.135°-α C.2α-180° D.180°-α
二.填空题(共5小题)
13.如图,在正方形ABCD中,AB=3,延长BC至E,使CE=2,连接AE.CF平分∠DCE交AE于F,连接DF,则DF的长为 ______.
14.如图,在矩形ABCD中,E是DC上一点,AE=AB,AB=2AD,则∠EBC的度数是______.
15.如图,菱形ABCD的周长为20,对角线AC,BD相交于点O,AC=8,DE⊥BC于点E,连接OE,则OE的长度为______.
16.如图,正方形ABCD的边长为6,点E,F分别是边BC,CD上的点,且BE=CF=2,
连接AE,AF,AE的垂直平分线分别交AB,AE,AF,CD于点G,M,N,H,则MN的长为 ______.
17.如图,点E是正方形ABCD的边BC延长线一点,连接AE交CD于F,作∠AEG=∠AEB,EG交CD的延长线于G,连接AG,当CE=BC=4时,作FH⊥AG于H,连接DH,则:①点F是CD的中点;②DH=1;③;④∠ADH=45°.其中正确的结论有______.
三.解答题(共5小题)
18.如图,在 ABCD中,AD>AB,AE平分∠BAD,交BC于点E,过点E作EF∥AB交AD于点F.
(1)求证:四边形ABEF是菱形;
(2)若菱形ABEF的周长为16,∠EBA=120°,求AE的大小.
19.如图,在 ABCD中,对角线AC,BD交于点O,过点A作AE⊥BC于点E,延长BC到点F,使CF=BE,连接DF.
(1)求证:四边形ADFE是矩形;
(2)连接OF,若AD=4,EC=3,∠BAE=30°,求OF的长度.
20.如图,在菱形ABCD中,对角线AC,BD交于点O,AE⊥BC交CB延长线于点E,CF∥AE交AD延长线于点F.
(1)求证:四边形AECF是矩形;
(2)连接OE,若BD=10,AD=13,求线段OE的长.
21.如图,在边长为4的正方形ABCD中,E,F分别为边BC,DC上的点,且BE=DF,过F点作AE的垂线交AB于H.
(1)求证:AE=HF.
(2)请写出AH与BE之间的数量关系并证明.
22.如图1,四边形ABCD为正方形,E为对角线AC上一点,连接DE,BE.
(1)求证:BE=DE;
(2)如图2,过点E作EF⊥DE,交边BC于点F,以DE,EF为邻边作矩形DEFG,连接CG.
①求证:矩形DEFG是正方形;
②若正方形ABCD的边长为9,CG=3,求正方形DEFG的边长.
青岛版八年级下 第6章 平行四边形
(参考答案)
一.选择题(共12小题)
1、C 2、A 3、B 4、A 5、D 6、A 7、C 8、B 9、B 10、C 11、D 12、A
二.填空题(共5小题)
13、; 14、15°; 15、3; 16、; 17、①③④;
三.解答题(共5小题)
18、(1)证明:∵ ABCD
∴BC∥AD,即 BE∥AF
∵EF∥AB
∴四边形ABEF为平行四边形
∵AE平分∠BAF
∴∠EAB=∠EAF
∵BC∥AD
∴∠BEA=∠EAF
∴∠BEA=∠BAE
∴AB=BE
∴四边形ABEF是菱形
(2)解:连接BF交AE于点O;则BF⊥AE于点O
∵BA=BE,∠EBA=120°
∴∠BEA=∠BAE=30°
∵菱形ABEF的周长为16
∴AB=4
在Rt△ABO中∠BAO=30°
∴
由勾股定理可得:AO=
∴AE=
19、(1)证明:∵在平行四边形ABCD中,
∴AB∥DC且AB=DC,
∴∠ABE=∠DCF,
在△ABE和△DCF中,
,
∴△ABE≌△DCF(SAS),
∴AE=DF,∠AEB=∠DFC=90°,
∴AE∥DF,
∴四边形ADFE是矩形;
(2)解:由(1)知:四边形ADFE是矩形,
∴EF=AD=4,
∵EC=3,
∴BE=CF=1,
∴BF=5,
Rt△ABE中,∠BAE=30°,
∴AB=2BE=2,
∴DF=AE==,
∴BD===2,
∵四边形ABCD是平行四边形,
∴OB=OD,
∴OF=BD=.
20、(1)证明:∵四边形ABCD是菱形,
∴AD∥BC.
∵CF∥AE,
∴四边形AECF是平行四边形.
∵AE⊥BC,
∴∠AEC=90°,
∴平行四边形AECF是矩形;
(2)解:如图,∵四边形ABCD是菱形,
∴OB=OD=BD=5,OA=OC,AC⊥BD,
∴OA===12,
∴AC=2OA=24,
∵AE⊥BC,
∴∠AEC=90°,
∴OE=AC=12.
21、(1)证明:过点F作FK⊥AB于点K,如图所示:
∴∠FKH=∠FKA=90°,
∵四边形ABCD是正方形,
∴AB=AD,∠B=∠BAD=∠D=90°,
∴∠FKA=∠BAD=∠D=90°,∠B=∠FKH=90°,
∴四边形ADFK是矩形,
∴AD=FK,DF=AK,
∴AB=FK,
∵FH⊥AE,∠FKH=90°,
∴∠BAE+∠AHF=90°,∠KFH+∠AHF=90°,
∴∠BAE=∠KFH,
在△BAE和△KFH中,
,
∴△BAE≌△KFH(ASA),
∴AE=HF;
(2)解:AH与BE之间的数量关系是,AH=2BE,证明如下:
∵△BAE≌△KFH,
∴BE=KH,
又∵BE=DF,DF=AK,
∴AK=BE,
∴AH=AK+KH=BE+BE=2BE.
22、(1)证明:∵四边形ABCD为正方形,
∴∠BAE=∠DAE=45°,AB=AD,
在△ABE和△ADE中,
,
∴△ABE≌△ADE(SAS),
∴BE=DE;
(2)①证明:如图,作EM⊥BC于M,EN⊥CD于N,
得矩形EMCN,
∴∠MEN=90°,
∵点E是正方形ABCD对角线上的点,
∴EM=EN,
∵∠DEF=90°,
∴∠DEN=∠MEF=90°-∠FEN,
∵∠DNE=∠FME=90°,
在△DEN和△FEM中,
,
∴△DEN≌△FEM(ASA),
∴EF=DE,
∵四边形DEFG是矩形,
∴矩形DEFG是正方形;
②解:∵正方形DEFG和正方形ABCD,
∴DE=DG,AD=DC,
∵∠CDG+∠CDE=∠ADE+∠CDE=90°,
∴∠CDG=∠ADE,
在△ADE和△CDG中,
,
∴△ADE≌△CDG(SAS),
∴AE=CG,∠DAE=∠DCG=45°,
∵∠ACD=45°,
∴∠ACG=∠ACD+∠DCG=90°,
∴CE⊥CG,
∴CE+CG=CE+AE=AC=AB=9.
∵CG=3,
∴CE=6,
连接EG,
∴EG===3,
∴DE=EG=3.
∴正方形DEFG的边长为3.
同课章节目录
- 第6章 平行四边形
- 6.1 平行四边形及其性质
- 6.2 平行四边形的判定
- 6.3 特殊的平行四边形
- 6.4 三角形的中位线定理
- 第7章 实数
- 7.1 算术平方根
- 7.2 勾股定理
- 7.3 根号2是有理数吗
- 7.4 勾股定理的逆定理
- 7.5 平方根
- 7.6 立方根
- 7.7 用计算器求平方根和立方根
- 7.8 实数
- 第8章 一元一次不等式
- 8.1 不等式的基本性质
- 8.2 一元一次不等式
- 8.3 列一元一次不等式解应用题
- 8.4 一元一次不等式组
- 第9章 二次根式
- 9.1 二次根式和它的性质
- 9.2 二次根式的加法与减法
- 9.3 二次根式的乘法与除法
- 第10章 一次函数
- 10.1 函数的图像
- 10.2 一次函数和它的图像
- 10.3 一次函数的性质
- 10.4 一次函数与二元一次方程
- 10.5 一次函数与一元一次不等式
- 10.6 一次函数的应用
- 第11章 图形的平移与旋转
- 11.1 图形的平移
- 11.2 图形的旋转
- 11.3 图形的中心对称
