第十九章一次函数单元测试卷 (含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十九章一次函数单元测试卷 (含答案) 2024-2025学年人教版八年级数学下册 |  | |
| 格式 | docx | ||
| 文件大小 | 118.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 21:12:47 | ||
图片预览



文档简介
第十九章一次函数单元测试卷
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.下列各曲线中表示y是x的函数的是 ( )
2.某地某一时刻的地面温度为10℃,高度每增加1km,温度下降4℃,则下列说法中:①10℃是常量;②高度是变量;③温度是变量;④该地某一高度这一时刻的温度y(℃)与高度x(km)的关系式为 y=10-4x.正确的是 ( )
A.①②③ B.②③④ C.①③④ D.①②③④
3.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图19-1所示.下列说法中正确的是 ( )
A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60m/min
C.小涛从报亭返回家中的平均速度是80m/min
D.小涛在报亭看报用了 15 min
4.已知一次函数y= kx+b,y随着x的增大而减小,且 kb>0,则这个函数的图象可能是( )
5.下列关于一次函数y=-2x+1的说法中,正确的是 ( )
A.图象经过第一、二、三象限 B.图象经过点(-2,1)
C.当x>1时,y<0 D. y随x的增大而增大
6.在平面直角坐标系中,将直线 向左平移1个单位,再向上平移3个单位得到直线l ,则直线l 的解析式为 ( )
A. y=-3x--9 B. y=-3x--2
C. y=-3x+2 D. y=-3x+9
7.在平面直角坐标系中,点 A,B的坐标分别为(2m-2,3),(m,3),且点A在点B 的左侧,若线段 AB 与直线y=--2x+1相交,则m的取值范围是 ( )
B.-1≤m≤1
D.0≤m≤1
8.如图19-2所示,购买一种苹果,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA 和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 ( )
A.1元 B.2元 C.3元 D.4元
9.如图19-3,直线 都与直线l垂直,垂足分别为M,N,MN=1.正方形 ABCD的边长为 对角线 AC在直线l上,且点 C 位于点M 处.将正方形ABCD沿l向右平移,直到点A与点 N 重合为止,记点 C平移的距离为x,正方形ABCD 的边位于 之间部分的长度和为y,则y关于x的函数图象大致为 ( )
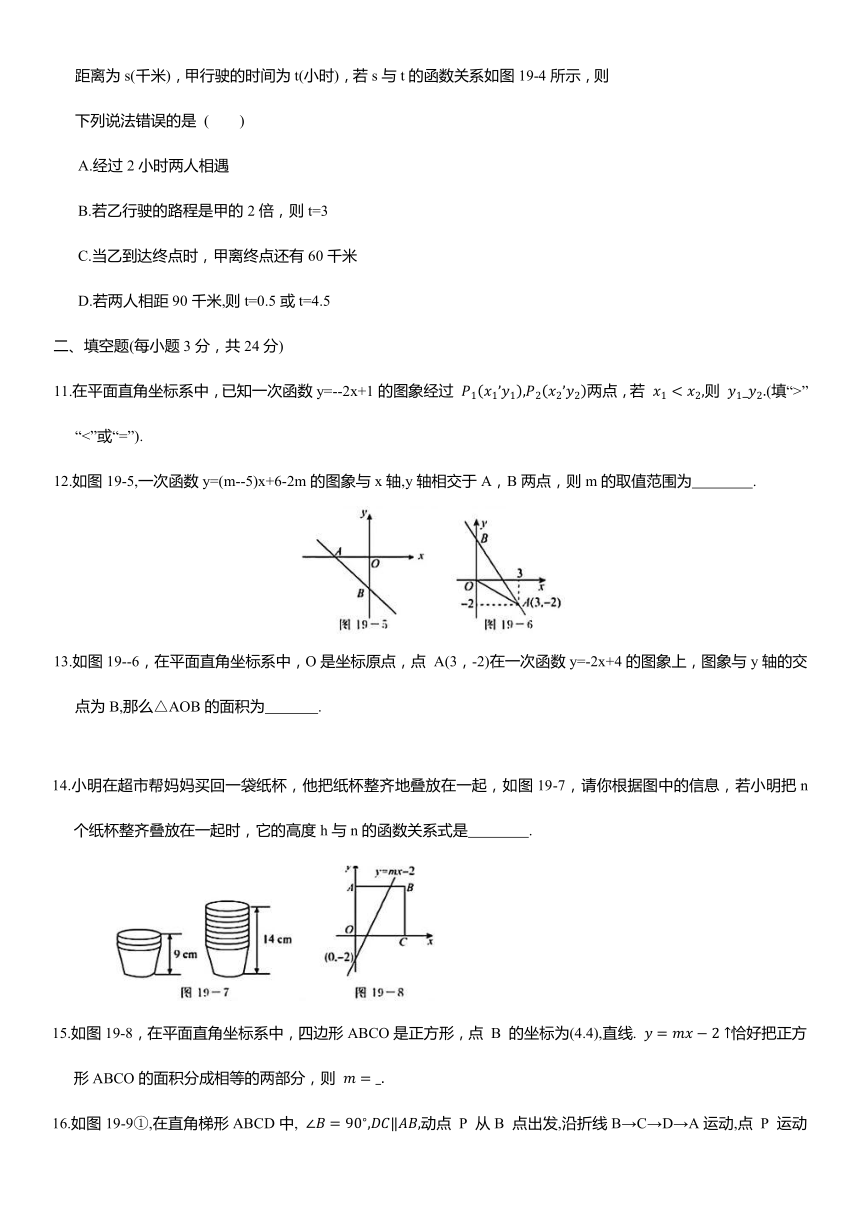
10.已知A,B两地相距120千米,甲、乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从 A 地前往B地,同时乙骑摩托车从 B 地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图19-4所示,则下列说法错误的是 ( )
A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
二、填空题(每小题3分,共24分)
11.在平面直角坐标系中,已知一次函数y=--2x+1的图象经过 两点,若 则 (填“>”“<”或“=”).
12.如图19-5,一次函数y=(m--5)x+6-2m的图象与x轴,y轴相交于A,B两点,则m的取值范围为 .
13.如图19--6,在平面直角坐标系中,O是坐标原点,点 A(3,-2)在一次函数y=-2x+4的图象上,图象与y轴的交点为B,那么△AOB的面积为 .
14.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图19-7,请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系式是 .
15.如图19-8,在平面直角坐标系中,四边形ABCO是正方形,点 B 的坐标为(4.4),直线. 恰好把正方形ABCO的面积分成相等的两部分,则
16.如图19-9①,在直角梯形ABCD中, 动点 P 从B 点出发,沿折线B→C→D→A运动,点 P 运动的速度为2个单位长度 /秒,设点 P 运动的时间为x秒, 的面积为y,若y关于x的函数图象如图19-9②所示,则M点的纵坐标为 .
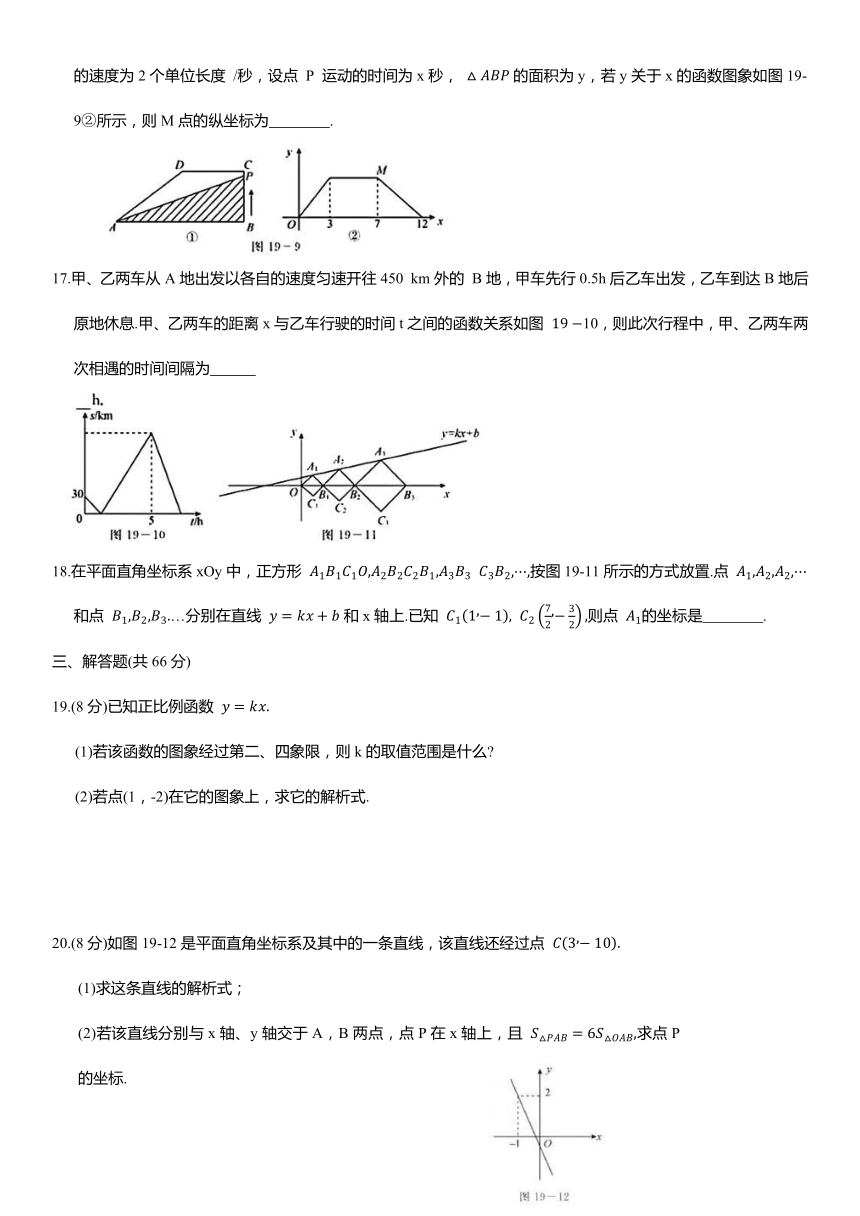
17.甲、乙两车从A地出发以各自的速度匀速开往450 km外的 B地,甲车先行0.5h后乙车出发,乙车到达B地后原地休息.甲、乙两车的距离x与乙车行驶的时间t之间的函数关系如图 10,则此次行程中,甲、乙两车两次相遇的时间间隔为
18.在平面直角坐标系xOy中,正方形 按图19-11所示的方式放置.点 和点 …分别在直线 和x轴上.已知 则点 的坐标是 .
三、解答题(共66分)
19.(8分)已知正比例函数
(1)若该函数的图象经过第二、四象限,则k的取值范围是什么
(2)若点(1,-2)在它的图象上,求它的解析式.
20.(8分)如图19-12是平面直角坐标系及其中的一条直线,该直线还经过点
(1)求这条直线的解析式;
(2)若该直线分别与x轴、y轴交于A,B两点,点P在x轴上,且 求点P的坐标.
21.(8分)如图 直线l 与x轴,y轴分别交于点A,B.将 绕点O顺时针旋转 得到 直线 交l于点C.
(1)求 两点的坐标及直线 的解析式:
(2)求 的面积.
22.(10分)如图19-14,直线L 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A 点以每秒1个单位的速度沿x轴向左移动.
(1)求 A、B两点的坐标;
(2)求 的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时 并求此时M点的坐标.
23.(10分)某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案;
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省
(3)设租车总费用为y(元),租用甲车x(辆),请写出函数解析式.
24.(10分)某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元
(2)根据消费需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数解析式,并说明当m为何值时所获利润最大 最大利润是多少
25.(12分)小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与行驶时间x(分钟)之间的函数图象如图19-15所示.
(1)求点 A 的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车 并求此时他们距学校站点的路程.
第十九章测试卷
1. A 2. D 3.1) 1. B 5. C 6. B 7. A 8. B 9. A 10. B11.> 12.319.解:(1)∵该函数的图象经过第二,四象限.∴k<0.
(2)当r=1. y=-2时,则k=-2,即y=-2. r.
20.解:(1)设直线的解析式为 y= ks-b.
由图可知,直线经过点(-1,2).
又已知直线经过点C(3,-10)。
分别把坐标代入解析式中,得 解得
∴直线的解析式为y=-3x-1.
(2)由y=-3x-1.令y=0.解得
令x=0,解得y=-1.
∴A. B两点的坐标分别为A(- . ). B(0.-1).
设点 P的坐标为P(m,0).
则
由S rn=6S ……得
从而得 或
或
即点P 的坐标为 成
21.解:(1)∵令x=0,则y=4.令y=0,则x=2.
∴A(2.0). B(0.4).
由图形旋转的性质可知. A'(0.-2). B'(4.0).
设过A'(0, 2),B'(4.0)的直线的解析式为 y= kx+b(k≠0).
则 解得
故直线A'B'的解析式.为
(2)由过A'.B'两点的直线的解析式为
得 解得
22.解:(1)对于直线AB
当. r=0时. y=2;当y=0时. x=1.
则A、B两点的坐标分别为A(1,0)、B(0,2).
(2)∵C(0.4),A(4.0)∴()C=()A=4.
当1>1时. 21-8.
(3)分为两种情况:①当M在OA 上时. OB-OM-2.△COM≌△AOB.
∴AM-()A-0M-4-2-2.
∴动点M从A 点以每秒1个单位的速度沿x轴相左移动2个单位,所需要的时间是2 秒钟:M(2.0).
②当M在AO的延长线上时. OM-()B=2.△OOM≌△AOB.
则M(-2.0),此时所需要的时间1-[1-(-2)]-6秒。
∴当1=2或6时,△(C)M≌△AOB,M点的坐标是(2,0)或(--2.0).
23.解: (1) 设 和 用 甲 车 x 辆,则 乙 车(10 - x) 辆。
解得 1≤x≤7.5.
∴有四种租车方案。
方案一:甲种车:4辆.乙种车6辆:
方案二:甲种车5辆.乙种车5辆:
方案三:甲种车6辆.乙种车1辆:
方案四:甲种车7辆,乙种车3辆。
(2)由题意可得,甲车的租金为每辆2000元,乙车的租金为每辆1800元。
∴甲车租得越少费用越低。
∴方案一:甲种车4辆,乙种车6辆使租车费用最省。
(3)函数解析式是 y=2 000. r +1 800(10-3)=200. x+18000(4≤x≤7).
即函数解析式是y-200x+18000(4≤x≤7).
24.解:(1)设甲种羽毛球每筒的售价为x元,乙种羽毛球每筒的售价为y元。根据题意可得 解得
答:该网店甲种羽毛球每筒的售价为60元,乙种羽毛球每筒的售价为45元.
(2)①若购进甲种羽毛球m筒,则乙种羽毛球为(200-m)筒。
根据题意可得 解得75方案一:购进甲种羽毛球76筒,乙种羽毛球为124筒:
方案二:购进甲种羽毛球77筒.乙种羽毛球为123筒:
方案三:购进甲种羽毛球78筒,乙种羽毛球为122筒。
②根据题意可得W=(60-50)m+(45-10)(200-m)=5m+1000.∵5>0.∴W随m的增大面增大,[175∴当m=78时,W 最大. W 最大值为1390.
答:当m=78时,所获利润最大,最大利润为1390元.
25.解:(1)校车的速度为3÷1=0.75(千米/分).点A 的纵坐标m的值为3+0.75×(8-6)=4.5.
答:点A 的纵坐标m的值为 1.5.
(2)因为m=1.5,所以∧(8.4.5),B(10.1.5).
因为 所以C(16.9),E(15.9),F(9.0)。
设线段BC'的解析式为y=k,x+b,(10≤x≤16).
则 解得 所以
设线段 EF 的解析式为y=k. x+b.(9≤x≤15)。
则 解已 所以
山 解得
因为11-9=5(分钟). 千米).
所以小刚乘坐出租车出发后经过5分钟追到小强所乘坐的校车,此时他们距学校站点的路程为
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.下列各曲线中表示y是x的函数的是 ( )
2.某地某一时刻的地面温度为10℃,高度每增加1km,温度下降4℃,则下列说法中:①10℃是常量;②高度是变量;③温度是变量;④该地某一高度这一时刻的温度y(℃)与高度x(km)的关系式为 y=10-4x.正确的是 ( )
A.①②③ B.②③④ C.①③④ D.①②③④
3.周日,小涛从家沿着一条笔直的公路步行去报亭看报,看了一段时间后,他按原路返回家中,小涛离家的距离y(单位:m)与他所用的时间t(单位:min)之间的函数关系如图19-1所示.下列说法中正确的是 ( )
A.小涛家离报亭的距离是900m
B.小涛从家去报亭的平均速度是60m/min
C.小涛从报亭返回家中的平均速度是80m/min
D.小涛在报亭看报用了 15 min
4.已知一次函数y= kx+b,y随着x的增大而减小,且 kb>0,则这个函数的图象可能是( )
5.下列关于一次函数y=-2x+1的说法中,正确的是 ( )
A.图象经过第一、二、三象限 B.图象经过点(-2,1)
C.当x>1时,y<0 D. y随x的增大而增大
6.在平面直角坐标系中,将直线 向左平移1个单位,再向上平移3个单位得到直线l ,则直线l 的解析式为 ( )
A. y=-3x--9 B. y=-3x--2
C. y=-3x+2 D. y=-3x+9
7.在平面直角坐标系中,点 A,B的坐标分别为(2m-2,3),(m,3),且点A在点B 的左侧,若线段 AB 与直线y=--2x+1相交,则m的取值范围是 ( )
B.-1≤m≤1
D.0≤m≤1
8.如图19-2所示,购买一种苹果,付款金额y(元)与购买量x(千克)之间的函数图象由线段OA 和射线AB组成,则一次购买3千克这种苹果比分三次每次购买1千克这种苹果可节省 ( )
A.1元 B.2元 C.3元 D.4元
9.如图19-3,直线 都与直线l垂直,垂足分别为M,N,MN=1.正方形 ABCD的边长为 对角线 AC在直线l上,且点 C 位于点M 处.将正方形ABCD沿l向右平移,直到点A与点 N 重合为止,记点 C平移的距离为x,正方形ABCD 的边位于 之间部分的长度和为y,则y关于x的函数图象大致为 ( )
10.已知A,B两地相距120千米,甲、乙两人沿同一条公路匀速行驶,甲骑自行车以20千米/时从 A 地前往B地,同时乙骑摩托车从 B 地前往A地,设两人之间的距离为s(千米),甲行驶的时间为t(小时),若s与t的函数关系如图19-4所示,则下列说法错误的是 ( )
A.经过2小时两人相遇
B.若乙行驶的路程是甲的2倍,则t=3
C.当乙到达终点时,甲离终点还有60千米
D.若两人相距90千米,则t=0.5或t=4.5
二、填空题(每小题3分,共24分)
11.在平面直角坐标系中,已知一次函数y=--2x+1的图象经过 两点,若 则 (填“>”“<”或“=”).
12.如图19-5,一次函数y=(m--5)x+6-2m的图象与x轴,y轴相交于A,B两点,则m的取值范围为 .
13.如图19--6,在平面直角坐标系中,O是坐标原点,点 A(3,-2)在一次函数y=-2x+4的图象上,图象与y轴的交点为B,那么△AOB的面积为 .
14.小明在超市帮妈妈买回一袋纸杯,他把纸杯整齐地叠放在一起,如图19-7,请你根据图中的信息,若小明把n个纸杯整齐叠放在一起时,它的高度h与n的函数关系式是 .
15.如图19-8,在平面直角坐标系中,四边形ABCO是正方形,点 B 的坐标为(4.4),直线. 恰好把正方形ABCO的面积分成相等的两部分,则
16.如图19-9①,在直角梯形ABCD中, 动点 P 从B 点出发,沿折线B→C→D→A运动,点 P 运动的速度为2个单位长度 /秒,设点 P 运动的时间为x秒, 的面积为y,若y关于x的函数图象如图19-9②所示,则M点的纵坐标为 .
17.甲、乙两车从A地出发以各自的速度匀速开往450 km外的 B地,甲车先行0.5h后乙车出发,乙车到达B地后原地休息.甲、乙两车的距离x与乙车行驶的时间t之间的函数关系如图 10,则此次行程中,甲、乙两车两次相遇的时间间隔为
18.在平面直角坐标系xOy中,正方形 按图19-11所示的方式放置.点 和点 …分别在直线 和x轴上.已知 则点 的坐标是 .
三、解答题(共66分)
19.(8分)已知正比例函数
(1)若该函数的图象经过第二、四象限,则k的取值范围是什么
(2)若点(1,-2)在它的图象上,求它的解析式.
20.(8分)如图19-12是平面直角坐标系及其中的一条直线,该直线还经过点
(1)求这条直线的解析式;
(2)若该直线分别与x轴、y轴交于A,B两点,点P在x轴上,且 求点P的坐标.
21.(8分)如图 直线l 与x轴,y轴分别交于点A,B.将 绕点O顺时针旋转 得到 直线 交l于点C.
(1)求 两点的坐标及直线 的解析式:
(2)求 的面积.
22.(10分)如图19-14,直线L 与x轴、y轴分别交于A、B两点,在y轴上有一点C(0,4),动点M从A 点以每秒1个单位的速度沿x轴向左移动.
(1)求 A、B两点的坐标;
(2)求 的面积S与M的移动时间t之间的函数关系式;
(3)当t为何值时 并求此时M点的坐标.
23.(10分)某学校组织340名师生进行长途考察活动,带有行李170件,计划租用甲、乙两种型号的汽车10辆.经了解,甲车每辆最多能载40人和16件行李,乙车每辆最多能载30人和20件行李.
(1)请你帮助学校设计所有可行的租车方案;
(2)如果甲车的租金为每辆2 000元,乙车的租金为每辆1800元,问哪种可行方案使租车费用最省
(3)设租车总费用为y(元),租用甲车x(辆),请写出函数解析式.
24.(10分)某网店销售甲、乙两种羽毛球,已知甲种羽毛球每筒的售价比乙种羽毛球多15元,王老师从该网店购买了2筒甲种羽毛球和3筒乙种羽毛球,共花费255元.
(1)该网店甲、乙两种羽毛球每筒的售价各是多少元
(2)根据消费需求,该网店决定用不超过8780元购进甲、乙两种羽毛球共200筒,且甲种羽毛球的数量大于乙种羽毛球数量的 已知甲种羽毛球每筒的进价为50元,乙种羽毛球每筒的进价为40元.
①若设购进甲种羽毛球m筒,则该网店有哪几种进货方案
②若所购进羽毛球均可全部售出,请求出网店所获利润W(元)与甲种羽毛球进货量m(筒)之间的函数解析式,并说明当m为何值时所获利润最大 最大利润是多少
25.(12分)小强与小刚都住在安康小区,在同一所学校读书,某天早上,小强7:30从安康小区站乘坐校车去学校,途中需停靠两个站点才能到达学校站点,且每个站点停留2分钟,校车行驶途中始终保持匀速,当天早上,小刚7:39从安康小区站乘坐出租车沿相同路线出发,出租车匀速行驶,比小强乘坐的校车早1分钟到学校站点,他们乘坐的车辆从安康小区站出发所行驶路程y(千米)与行驶时间x(分钟)之间的函数图象如图19-15所示.
(1)求点 A 的纵坐标m的值;
(2)小刚乘坐出租车出发后经过多少分钟追到小强所乘坐的校车 并求此时他们距学校站点的路程.
第十九章测试卷
1. A 2. D 3.1) 1. B 5. C 6. B 7. A 8. B 9. A 10. B11.> 12.3
(2)当r=1. y=-2时,则k=-2,即y=-2. r.
20.解:(1)设直线的解析式为 y= ks-b.
由图可知,直线经过点(-1,2).
又已知直线经过点C(3,-10)。
分别把坐标代入解析式中,得 解得
∴直线的解析式为y=-3x-1.
(2)由y=-3x-1.令y=0.解得
令x=0,解得y=-1.
∴A. B两点的坐标分别为A(- . ). B(0.-1).
设点 P的坐标为P(m,0).
则
由S rn=6S ……得
从而得 或
或
即点P 的坐标为 成
21.解:(1)∵令x=0,则y=4.令y=0,则x=2.
∴A(2.0). B(0.4).
由图形旋转的性质可知. A'(0.-2). B'(4.0).
设过A'(0, 2),B'(4.0)的直线的解析式为 y= kx+b(k≠0).
则 解得
故直线A'B'的解析式.为
(2)由过A'.B'两点的直线的解析式为
得 解得
22.解:(1)对于直线AB
当. r=0时. y=2;当y=0时. x=1.
则A、B两点的坐标分别为A(1,0)、B(0,2).
(2)∵C(0.4),A(4.0)∴()C=()A=4.
当1>1时. 21-8.
(3)分为两种情况:①当M在OA 上时. OB-OM-2.△COM≌△AOB.
∴AM-()A-0M-4-2-2.
∴动点M从A 点以每秒1个单位的速度沿x轴相左移动2个单位,所需要的时间是2 秒钟:M(2.0).
②当M在AO的延长线上时. OM-()B=2.△OOM≌△AOB.
则M(-2.0),此时所需要的时间1-[1-(-2)]-6秒。
∴当1=2或6时,△(C)M≌△AOB,M点的坐标是(2,0)或(--2.0).
23.解: (1) 设 和 用 甲 车 x 辆,则 乙 车(10 - x) 辆。
解得 1≤x≤7.5.
∴有四种租车方案。
方案一:甲种车:4辆.乙种车6辆:
方案二:甲种车5辆.乙种车5辆:
方案三:甲种车6辆.乙种车1辆:
方案四:甲种车7辆,乙种车3辆。
(2)由题意可得,甲车的租金为每辆2000元,乙车的租金为每辆1800元。
∴甲车租得越少费用越低。
∴方案一:甲种车4辆,乙种车6辆使租车费用最省。
(3)函数解析式是 y=2 000. r +1 800(10-3)=200. x+18000(4≤x≤7).
即函数解析式是y-200x+18000(4≤x≤7).
24.解:(1)设甲种羽毛球每筒的售价为x元,乙种羽毛球每筒的售价为y元。根据题意可得 解得
答:该网店甲种羽毛球每筒的售价为60元,乙种羽毛球每筒的售价为45元.
(2)①若购进甲种羽毛球m筒,则乙种羽毛球为(200-m)筒。
根据题意可得 解得75
方案二:购进甲种羽毛球77筒.乙种羽毛球为123筒:
方案三:购进甲种羽毛球78筒,乙种羽毛球为122筒。
②根据题意可得W=(60-50)m+(45-10)(200-m)=5m+1000.∵5>0.∴W随m的增大面增大,[175
答:当m=78时,所获利润最大,最大利润为1390元.
25.解:(1)校车的速度为3÷1=0.75(千米/分).点A 的纵坐标m的值为3+0.75×(8-6)=4.5.
答:点A 的纵坐标m的值为 1.5.
(2)因为m=1.5,所以∧(8.4.5),B(10.1.5).
因为 所以C(16.9),E(15.9),F(9.0)。
设线段BC'的解析式为y=k,x+b,(10≤x≤16).
则 解得 所以
设线段 EF 的解析式为y=k. x+b.(9≤x≤15)。
则 解已 所以
山 解得
因为11-9=5(分钟). 千米).
所以小刚乘坐出租车出发后经过5分钟追到小强所乘坐的校车,此时他们距学校站点的路程为
