第十八章平行四边形 单元测试卷(含答案) 2024-2025学年人教版八年级数学下册
文档属性
| 名称 | 第十八章平行四边形 单元测试卷(含答案) 2024-2025学年人教版八年级数学下册 |
|
|
| 格式 | docx | ||
| 文件大小 | 144.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2025-06-19 00:00:00 | ||
图片预览




文档简介
第十八章平行四边形单元测试卷
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
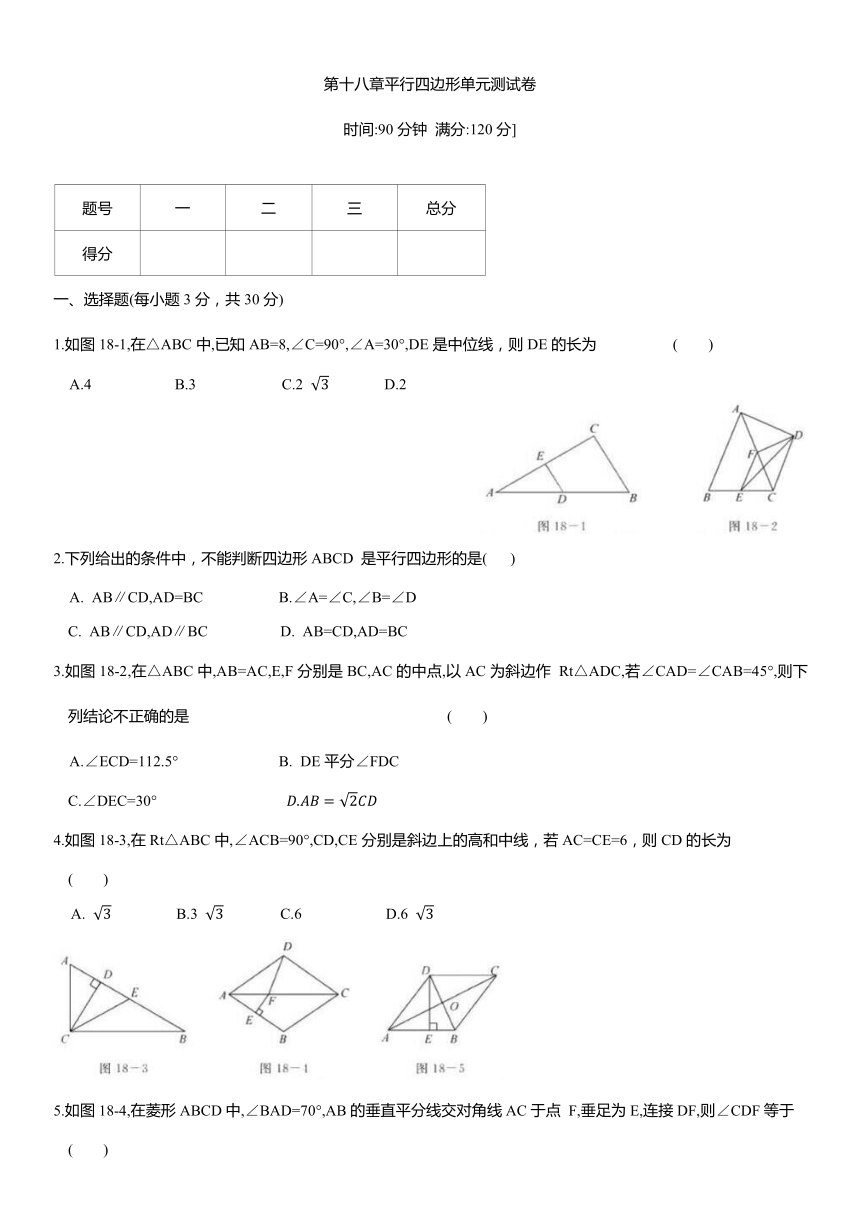
1.如图18-1,在△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为 ( )
A.4 B.3 C.2 D.2
2.下列给出的条件中,不能判断四边形ABCD 是平行四边形的是( )
A. AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C. AB∥CD,AD∥BC D. AB=CD,AD=BC
3.如图18-2,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作 Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是 ( )
A.∠ECD=112.5° B. DE平分∠FDC
C.∠DEC=30°
4.如图18-3,在Rt△ABC中,∠ACB=90°,CD,CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为 ( )
A. B.3 C.6 D.6
5.如图18-4,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点 F,垂足为E,连接DF,则∠CDF等于 ( )
A.55° B.65° C.75° D.85°
6.如图18-5,菱形ABCD的周长为40cm,对角线AC,BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm,②BE=4cm,③BD=4 cm,④AC=8 cm,⑤S菱形. Mcv=60cm ,其中正确的有 ( )
A.①②④⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
7.在探索“尺规三等分角”这个数学命题的过程中,曾利用了如图18-6.该图中,四边形ABCD是矩形,E是BA 延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是 ( )
A.7° B.21° C.23° D.24°
8.如图18-7,在△ABC中,点 D是边 BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交 AB,AC于E,F两点,下列说法正确的是 ( )
A.若AD⊥BC,则四边形 AEDF 是矩形
B.若AD垂直平分BC,则四边形 AEDF 是矩形
C.若BD=CD,则四边形 AEDF 是菱形
D.若AD平分∠BAC,则四边形 AEDF 是菱形
9.如图18-8是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是 ( )
10.如图18--9,点 E 在正方形ABCD 的对角线 AC 上,且 EC=2.5AE, Rt△FEG的两直角边 EF. EG 分别交BC,CD 于点M,N.若正方形的边长是a,则重叠部分四边形EMCN 的面积为 ( )
二、填空题(每小题3分,共24分)
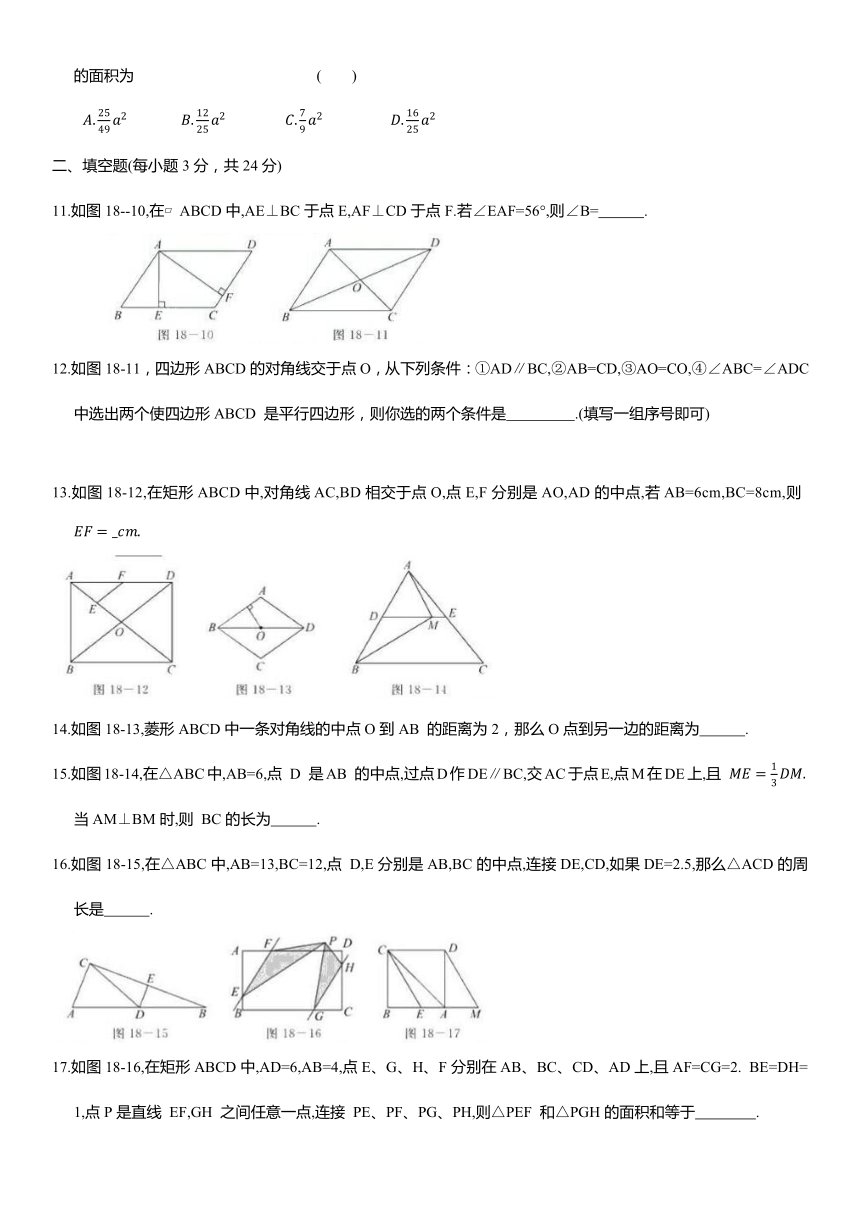
11.如图18--10,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B= .
12.如图18-11,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个使四边形ABCD 是平行四边形,则你选的两个条件是 .(填写一组序号即可)
13.如图18-12,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6cm,BC=8cm,则
14.如图18-13,菱形ABCD中一条对角线的中点O到AB 的距离为2,那么O点到另一边的距离为 .
15.如图18-14,在△ABC中,AB=6,点 D 是AB 的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且 当AM⊥BM时,则 BC的长为 .
16.如图18-15,在△ABC中,AB=13,BC=12,点 D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .
17.如图18-16,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2. BE=DH=1,点P是直线 EF,GH 之间任意一点,连接 PE、PF、PG、PH,则△PEF 和△PGH的面积和等于 .
18.如图18-17,已知正方形 ABCD,点 M 是边 BA 延长线上的动点(不与点 A 重合),且 AM三、解答题(共66分)
19.(8分)如图18-18,在 ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.
20.(8分)如图 的中线BD,CE相交于点O,F,G分别是BO,CO的中点,求证: 且
21.(8分)如图 在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.
(1)求证:
(2)若平行四边形 ABCD的面积为32,试求四边形 EBCD的面积.
22.(10分)如图18-21,在菱形ABCD中,F为对角线BD 上一点,点E为AB 延长线上一点, 求证:
23.(10分)如图18--22,在 ABCD中,AE⊥BC于点E,延长 2BC至F 点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
24.(10分)如图18-23,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判定四边形 AEGF是否为菱形,并说明理由.
25.(12分)如图18-24,在正方形ABCD中,E是边AB上的一动点(不与点 A、B重合),连接DE,点A 关于直线DE的对称点为F,连接 EF 并延长交 BC于点 G,连接 DG,过点 E作 交 DG的延长线于点 H,连接BH.
(1)求证:
(2)用等式表示线段BH与AE 的数量关系,并证明.
第十八章测试卷
1.1) 2. A 3. C 1. B 5. C 6. B 7. C 8. D 9. A 10. A11.56° 12.①③ 13.2.5 14.2 15.8 16.18 17.718.①②③
19.证明:∵四边形ABCD 是平行四边形,∴AD~BC,∠A=∠C.AD∥BC,∴∠E=∠F,∵BE=DF,∴AF=EC,在△AGF和△CHE中
∴△AGF≌△CHE(ASA).∴AG=CH.
20.证明:连接DE. FG.∵BD. CE是△ABC的中线,∴D. E是AC. AB边的中点,∴DE∥BC. DE= BC.同理:FG∥BC.边形,∴EF∥IX;. EF=DG;.
21.(1)证明:∵E是AB 边上的中点,∴AE=BE.∵AD∥BC.∴∠ADE=∠F.在△ADE 和△BFE 中.∠ADE=∠F.∠DEA=∠FEB,AE=BE.∴△ADE≌△BFE.∴AD=BF.
(2)解:过点 D作DM⊥AB于M.如图18-20.则 DM同时也是平行四边形ABCD的高.
22.证明:(1)∵四边形ABCD是菱形.∴CD=C'B.
在△CFD和△CEB中.∴△CFD≌△CEB(SSS).
(2)∵△CFD≌△CEB.∴∠CDB=∠CBE.∠DCF=∠BCE.∵四边形ABCD是菱形.∴∠CBD=∠ABD.∵CD=CB.∴∠CDB=∠CBD.∴∠ABD=∠CBD=∠CBE=60°.∴∠DC'B=60°.∴∠FCE=60°.∵CF=CE.∴∠CFE=∠CEF=60°.
23.(1)证明:∵CF=BE,∴CF⊥EC=BE⊥EC,即EF=BC,∵在∴四边形AEFD 是平行四边形.∵AE⊥BC.∴∠AEF=90°.∴四边形AEFD 是矩形.
(2)解:∵四边形 AEFD是矩形. DE=8.∴AF=DE=8.∵AB=6. BF=10.∴AB'+AF '=6' - 8' = 100 = BF'.∴∠BAF=90°.∵AE⊥BF,∴△ABF 的面
24.(1)证明:∴AF=FG.∴∠FAG=∠FGA.∵AG平分∠CAB.∴∠('A(i=∠FAG.∴∠('A(i=∠F(iA.∴AC∥F(;.∵DE⊥AC.∴FG⊥DE.∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∠CGE-∠GED.∴∠C=∠DHG=90'.∵F是AD 的中点. FG∥AE.∴11 是ED的中点.∴FG 是线段 ED的垂直平分线.∴GE=GD.∠GDE=∠GED.∴∠(GE=∠GDE.∴△ECG≌△GHD(AAS).
(2)证明:过点G作GP⊥AB于P.如答图18-1.
∵AG平分∠BAC,∴GC=GP.而AG=AG.
∴△(λG≌△PAG(H1.).∴AC=AP.
由(1)可得EG-1X;.
∴Rt△E('(;≌Rt△GPD(111.).
∴EC-PD.∴AD-AP+PD-AC|EC.
(3)解:四边形AEGF 是菱形。
证明:∵ AF-FG.由(1)得AE∥FG.∴四边形AEGF 是菱形.
25.证明:(1)如答图18-2,连接DF.
∵四边形 ABCD 是正方形.∴DA=DC.∠A=∠C=90°.
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE.
∴DA=DF=DC.∠DFE=∠A=90°.
∴∠DFG=90°.
在Rt△DFG和 Rt△DCG中.
∴Rt△DFG≌Rt△D((;(H1.).
∴GF=GC.
理由是:
证法…如答图18-3,在线段AD 上截取AM,使AM=AE.
∵AD=AB.
∴DM=BE.
由(1)知:∠1-∠2.∠3-∠4.
∵∠ADC=90°.
∴∠1+∠2+∠3÷∠4=90°.
∴2∠2+2∠3=90°,∴∠2+∠3=45°.
即∠EIX;=15°.∵EH⊥DE.
∴∠DEH=90°.△DEH 是等腰直角三角形.
∴∠AED-∠BEH=∠AED+∠1=90°. DE=EH.
∴∠1=∠BEH.
在△DME 和△EBH中
∴△DME≌△EBH(SAS).∴EM=BH.
Rt△AEM中.∠A=90°. AM=AE.
证法二:如答图18-4.过点 H 作 HN⊥AB于N.
∴∠ENH=90°.
山方法 一 可知: DE = EH.∠1=∠NEH.
在△DAE和△ENH中.
∴△DAE≌△ENH(AAS).∴AE=HN. AD=EN.
∵AD=AB.∴AB=EN=AE+BE=BE+BN.
∴AE=BN-11N.∴△BNH是等腰直角三角形.
时间:90分钟 满分:120分]
题号 一 二 三 总分
得分
一、选择题(每小题3分,共30分)
1.如图18-1,在△ABC中,已知AB=8,∠C=90°,∠A=30°,DE是中位线,则DE的长为 ( )
A.4 B.3 C.2 D.2
2.下列给出的条件中,不能判断四边形ABCD 是平行四边形的是( )
A. AB∥CD,AD=BC B.∠A=∠C,∠B=∠D
C. AB∥CD,AD∥BC D. AB=CD,AD=BC
3.如图18-2,在△ABC中,AB=AC,E,F分别是BC,AC的中点,以AC为斜边作 Rt△ADC,若∠CAD=∠CAB=45°,则下列结论不正确的是 ( )
A.∠ECD=112.5° B. DE平分∠FDC
C.∠DEC=30°
4.如图18-3,在Rt△ABC中,∠ACB=90°,CD,CE分别是斜边上的高和中线,若AC=CE=6,则CD的长为 ( )
A. B.3 C.6 D.6
5.如图18-4,在菱形ABCD中,∠BAD=70°,AB的垂直平分线交对角线AC于点 F,垂足为E,连接DF,则∠CDF等于 ( )
A.55° B.65° C.75° D.85°
6.如图18-5,菱形ABCD的周长为40cm,对角线AC,BD相交于点O,DE⊥AB,垂足为E,DE:AB=4:5,则下列结论:①DE=8cm,②BE=4cm,③BD=4 cm,④AC=8 cm,⑤S菱形. Mcv=60cm ,其中正确的有 ( )
A.①②④⑤ B.①②③④ C.①③④⑤ D.①②③④⑤
7.在探索“尺规三等分角”这个数学命题的过程中,曾利用了如图18-6.该图中,四边形ABCD是矩形,E是BA 延长线上一点,F是CE上一点,∠ACF=∠AFC,∠FAE=∠FEA.若∠ACB=21°,则∠ECD的度数是 ( )
A.7° B.21° C.23° D.24°
8.如图18-7,在△ABC中,点 D是边 BC上的点(与B,C两点不重合),过点D作DE∥AC,DF∥AB,分别交 AB,AC于E,F两点,下列说法正确的是 ( )
A.若AD⊥BC,则四边形 AEDF 是矩形
B.若AD垂直平分BC,则四边形 AEDF 是矩形
C.若BD=CD,则四边形 AEDF 是菱形
D.若AD平分∠BAC,则四边形 AEDF 是菱形
9.如图18-8是边长为10cm的正方形铁片,过两个顶点剪掉一个三角形,以下四种剪法中,裁剪线长度所标的数据(单位:cm)不正确的是 ( )
10.如图18--9,点 E 在正方形ABCD 的对角线 AC 上,且 EC=2.5AE, Rt△FEG的两直角边 EF. EG 分别交BC,CD 于点M,N.若正方形的边长是a,则重叠部分四边形EMCN 的面积为 ( )
二、填空题(每小题3分,共24分)
11.如图18--10,在 ABCD中,AE⊥BC于点E,AF⊥CD于点F.若∠EAF=56°,则∠B= .
12.如图18-11,四边形ABCD的对角线交于点O,从下列条件:①AD∥BC,②AB=CD,③AO=CO,④∠ABC=∠ADC中选出两个使四边形ABCD 是平行四边形,则你选的两个条件是 .(填写一组序号即可)
13.如图18-12,在矩形ABCD中,对角线AC,BD相交于点O,点E,F分别是AO,AD的中点,若AB=6cm,BC=8cm,则
14.如图18-13,菱形ABCD中一条对角线的中点O到AB 的距离为2,那么O点到另一边的距离为 .
15.如图18-14,在△ABC中,AB=6,点 D 是AB 的中点,过点D作DE∥BC,交AC于点E,点M在DE上,且 当AM⊥BM时,则 BC的长为 .
16.如图18-15,在△ABC中,AB=13,BC=12,点 D,E分别是AB,BC的中点,连接DE,CD,如果DE=2.5,那么△ACD的周长是 .
17.如图18-16,在矩形ABCD中,AD=6,AB=4,点E、G、H、F分别在AB、BC、CD、AD上,且AF=CG=2. BE=DH=1,点P是直线 EF,GH 之间任意一点,连接 PE、PF、PG、PH,则△PEF 和△PGH的面积和等于 .
18.如图18-17,已知正方形 ABCD,点 M 是边 BA 延长线上的动点(不与点 A 重合),且 AM
19.(8分)如图18-18,在 ABCD中,点E、F分别在边CB、AD的延长线上,且BE=DF,EF分别与AB、CD交于点G、H.求证:AG=CH.
20.(8分)如图 的中线BD,CE相交于点O,F,G分别是BO,CO的中点,求证: 且
21.(8分)如图 在平行四边形ABCD中,E为AB边上的中点,连接DE并延长,交CB的延长线于点F.
(1)求证:
(2)若平行四边形 ABCD的面积为32,试求四边形 EBCD的面积.
22.(10分)如图18-21,在菱形ABCD中,F为对角线BD 上一点,点E为AB 延长线上一点, 求证:
23.(10分)如图18--22,在 ABCD中,AE⊥BC于点E,延长 2BC至F 点使CF=BE,连接AF,DE,DF.
(1)求证:四边形AEFD是矩形;
(2)若AB=6,DE=8,BF=10,求AE的长.
24.(10分)如图18-23,△ABC中,D是AB上一点,DE⊥AC于点E,F是AD的中点,FG⊥BC于点G,与DE交于点H,若FG=AF,AG平分∠CAB,连接GE,GD.
(1)求证:△ECG≌△GHD;
(2)小亮同学经过探究发现:AD=AC+EC.请你帮助小亮同学证明这一结论;
(3)若∠B=30°,判定四边形 AEGF是否为菱形,并说明理由.
25.(12分)如图18-24,在正方形ABCD中,E是边AB上的一动点(不与点 A、B重合),连接DE,点A 关于直线DE的对称点为F,连接 EF 并延长交 BC于点 G,连接 DG,过点 E作 交 DG的延长线于点 H,连接BH.
(1)求证:
(2)用等式表示线段BH与AE 的数量关系,并证明.
第十八章测试卷
1.1) 2. A 3. C 1. B 5. C 6. B 7. C 8. D 9. A 10. A11.56° 12.①③ 13.2.5 14.2 15.8 16.18 17.718.①②③
19.证明:∵四边形ABCD 是平行四边形,∴AD~BC,∠A=∠C.AD∥BC,∴∠E=∠F,∵BE=DF,∴AF=EC,在△AGF和△CHE中
∴△AGF≌△CHE(ASA).∴AG=CH.
20.证明:连接DE. FG.∵BD. CE是△ABC的中线,∴D. E是AC. AB边的中点,∴DE∥BC. DE= BC.同理:FG∥BC.边形,∴EF∥IX;. EF=DG;.
21.(1)证明:∵E是AB 边上的中点,∴AE=BE.∵AD∥BC.∴∠ADE=∠F.在△ADE 和△BFE 中.∠ADE=∠F.∠DEA=∠FEB,AE=BE.∴△ADE≌△BFE.∴AD=BF.
(2)解:过点 D作DM⊥AB于M.如图18-20.则 DM同时也是平行四边形ABCD的高.
22.证明:(1)∵四边形ABCD是菱形.∴CD=C'B.
在△CFD和△CEB中.∴△CFD≌△CEB(SSS).
(2)∵△CFD≌△CEB.∴∠CDB=∠CBE.∠DCF=∠BCE.∵四边形ABCD是菱形.∴∠CBD=∠ABD.∵CD=CB.∴∠CDB=∠CBD.∴∠ABD=∠CBD=∠CBE=60°.∴∠DC'B=60°.∴∠FCE=60°.∵CF=CE.∴∠CFE=∠CEF=60°.
23.(1)证明:∵CF=BE,∴CF⊥EC=BE⊥EC,即EF=BC,∵在∴四边形AEFD 是平行四边形.∵AE⊥BC.∴∠AEF=90°.∴四边形AEFD 是矩形.
(2)解:∵四边形 AEFD是矩形. DE=8.∴AF=DE=8.∵AB=6. BF=10.∴AB'+AF '=6' - 8' = 100 = BF'.∴∠BAF=90°.∵AE⊥BF,∴△ABF 的面
24.(1)证明:∴AF=FG.∴∠FAG=∠FGA.∵AG平分∠CAB.∴∠('A(i=∠FAG.∴∠('A(i=∠F(iA.∴AC∥F(;.∵DE⊥AC.∴FG⊥DE.∵FG⊥BC,∴DE∥BC,∴AC⊥BC,∠CGE-∠GED.∴∠C=∠DHG=90'.∵F是AD 的中点. FG∥AE.∴11 是ED的中点.∴FG 是线段 ED的垂直平分线.∴GE=GD.∠GDE=∠GED.∴∠(GE=∠GDE.∴△ECG≌△GHD(AAS).
(2)证明:过点G作GP⊥AB于P.如答图18-1.
∵AG平分∠BAC,∴GC=GP.而AG=AG.
∴△(λG≌△PAG(H1.).∴AC=AP.
由(1)可得EG-1X;.
∴Rt△E('(;≌Rt△GPD(111.).
∴EC-PD.∴AD-AP+PD-AC|EC.
(3)解:四边形AEGF 是菱形。
证明:∵ AF-FG.由(1)得AE∥FG.∴四边形AEGF 是菱形.
25.证明:(1)如答图18-2,连接DF.
∵四边形 ABCD 是正方形.∴DA=DC.∠A=∠C=90°.
∵点A关于直线DE的对称点为F,
∴△ADE≌△FDE.
∴DA=DF=DC.∠DFE=∠A=90°.
∴∠DFG=90°.
在Rt△DFG和 Rt△DCG中.
∴Rt△DFG≌Rt△D((;(H1.).
∴GF=GC.
理由是:
证法…如答图18-3,在线段AD 上截取AM,使AM=AE.
∵AD=AB.
∴DM=BE.
由(1)知:∠1-∠2.∠3-∠4.
∵∠ADC=90°.
∴∠1+∠2+∠3÷∠4=90°.
∴2∠2+2∠3=90°,∴∠2+∠3=45°.
即∠EIX;=15°.∵EH⊥DE.
∴∠DEH=90°.△DEH 是等腰直角三角形.
∴∠AED-∠BEH=∠AED+∠1=90°. DE=EH.
∴∠1=∠BEH.
在△DME 和△EBH中
∴△DME≌△EBH(SAS).∴EM=BH.
Rt△AEM中.∠A=90°. AM=AE.
证法二:如答图18-4.过点 H 作 HN⊥AB于N.
∴∠ENH=90°.
山方法 一 可知: DE = EH.∠1=∠NEH.
在△DAE和△ENH中.
∴△DAE≌△ENH(AAS).∴AE=HN. AD=EN.
∵AD=AB.∴AB=EN=AE+BE=BE+BN.
∴AE=BN-11N.∴△BNH是等腰直角三角形.
